基于动态关联表征与图网络建模的分布式光伏超短期功率预测

王玉庆，徐 飞，刘志坚，甄 钊，，王 飞，4，5

（1.华北电力大学电力工程系，河北省保定市 071003；2.新型电力系统运行与控制全国重点实验室（清华大学），北京市 100084；3.华北电力大学动力工程系，河北省保定市 071003；4.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；5.河北省分布式储能与微网重点实验室（华北电力大学），河北省保定市 071003）

0 引言

分布式光伏可在用户侧安装与消纳，减少长距离输送导致的线路损耗，在新型电力系统建设中发挥重要作用［1-2］。截至2022 年底，国内分布式光伏装机容量已达157.6 GW，其新增容量连续两年超过集中式光伏，发展迅猛［3］。然而，光伏出力易受天气因素影响，具有极强的随机波动性。大规模分布式光伏的接入，一方面加剧了配电网负荷短时波动，影响电力实时平衡，制约负荷预测精度提升［4-7］；另一方面，其出力与负荷特性不匹配造成消纳难题，为有源配电网运行带来严峻挑战。因此，亟需精准功率预测为有源配电网调度运行、分布式光伏消纳等提供有力支撑［8-9］。

现有光伏功率预测方法可分为物理建模与数据驱动方法［10-12］。物理建模方法依据光伏发电原理，利用气象信息与场站参数构建功率预测模型。例如，文献［13］考虑分布式光伏安装的方位角、倾角等场站设计信息实现发电量预测。这类方法可解释性强但建模复杂，且不适用于设施参数难获取的场景。数据驱动法通过分析气象因素与功率关系实现功率预测［14］。文献［15］考虑集中式与分布式光伏位置差异导致的数据时移，将集中式场站气象数据时移修正后用于分布式光伏，提升了其功率预测精度。然而，上述方法均未考虑到分布式光伏间内在联系，功率预测精度提升有限。

由于位置临近，处于相同地理、气候环境下的同时刻出力呈现相似的变化［16］，各分布式光伏间具有空间相关性，且其出力固有时间自相关性。各站点历史功率会与邻近站点未来出力有一定关联关系，即时空关联性。为利用关联信息提升功率预测精度，文献［17］将邻近光伏站点出力作为模型输入预测目标站出力，但该处理方式较简单且未考虑场站间关联性强弱。文献［18］基于图结构数据构建预测模型以更有效挖掘关联信息，该图结构将各场站及其出力分别作为节点与节点特征，节点间关联关系由历史功率相关性与地理距离定义并固定［19-21］。这种静态关联关系构建方式在分布式光伏出力长期稳定情况下，可取得较好预测效果。然而，受天气因素影响［22］，光伏出力易发生短时波动，各分布式光伏场站关联性处于动态变化。以恒定的场站间关联关系去考虑复杂的集群出力序列，无法反映天气影响下分布式光伏出力短时变化，难以实现功率预测精度提升。

目前，在交通流量预测和风功率预测方面已有动态图神经的相关研究。文献［23-24］基于地理距离建立交通流量初始图结构，然后分别利用时空卷积与时空注意力机制实现对节点连接关系的动态挖掘。对于出力受多元气象因素影响的分布式光伏，以地理距离为主导表征动态关系并不适用于其功率预测建模。而文献［25］仅实时计算简单的风功率互信息数，难以深层挖掘节点特征、有效表征节点间的复杂关联性。分布式光伏出力可看作多个相对稳定分量与波动分量的叠加，功率序列复杂，且不同分量下分布式光伏间呈现不同关联关系。因此，直接利用功率挖掘场站间关联关系难以取得理想效果。

为此，本文提出了基于时空关联动态表征与图网络建模的分布式光伏功率预测方法。首先，利用变分模态分解（variational mode decomposition，VMD）将功率序列分解为多个子序列，降低出力波动性对关联性挖掘的不利影响。然后，利用数据驱动有效表征场站间时空关联关系，并构建分布式光伏动态图结构数据。最后，为各分量构建考虑动态时空关联性的动态图卷积网络（dynamic graph convolutional network，DGCN）预测模型，精细化挖掘关联关系，实现区域分布式光伏超短期功率的精准预测。

1 图网络建模与时空关联性分析

1.1 分布式光伏图结构数据

为充分挖掘分布式光伏间时空特征信息，根据其关联关系，可将N个分布式光伏定义为图结构数据G=(V，E，A)，其中，V 为节点集合，图节点vi∈V为分布式光伏站点，节点数目为|V|=N；E 为连接vi与vj两节点的边eij的集合；邻接矩阵A∈RN×N为任意两场站关联关系的数学表征。根据各节点特征相关性来构建邻接矩阵，如式（1）所示。

1.2 基于图卷积网络的时空特征提取

对分布式光伏图结构数据的有效挖掘可以实现功率预测精度的提升。由于图卷积网络（graph convolutional network，GCN）对图结构数据问题强大的处理能力，其在电力系统逐渐得到应用。GCN可分为谱域GCN 和空域GCN，其中，空域GCN 建模相对简单灵活［25］。空域GCN 的核心思想是对输入信息进行卷积操作来聚合节点及其邻接节点，以获得各节点新的表示。基于更合理的分布式光伏图结构数据，可以使GCN 更好地发挥其时空特征提取能力，实现功率预测精度有效提升。

1.3 分布式光伏动态关联性

常用的图结构表征方式多依据长期历史特征来表征图节点的静态关联关系。值得注意的是，场站间关系处于动态变化，利用文献［25］的方式，逐时计算分布式光伏站点不同天气下的短时出力相关性情况如图1 所示，其中，相关性利用皮尔逊系数计算得到。晴天条件下，分布式光伏出力稳定，具有一定的规律性，场站间出力相关性变化程度较小；阴雨条件下，分布式光伏出力波动剧烈。

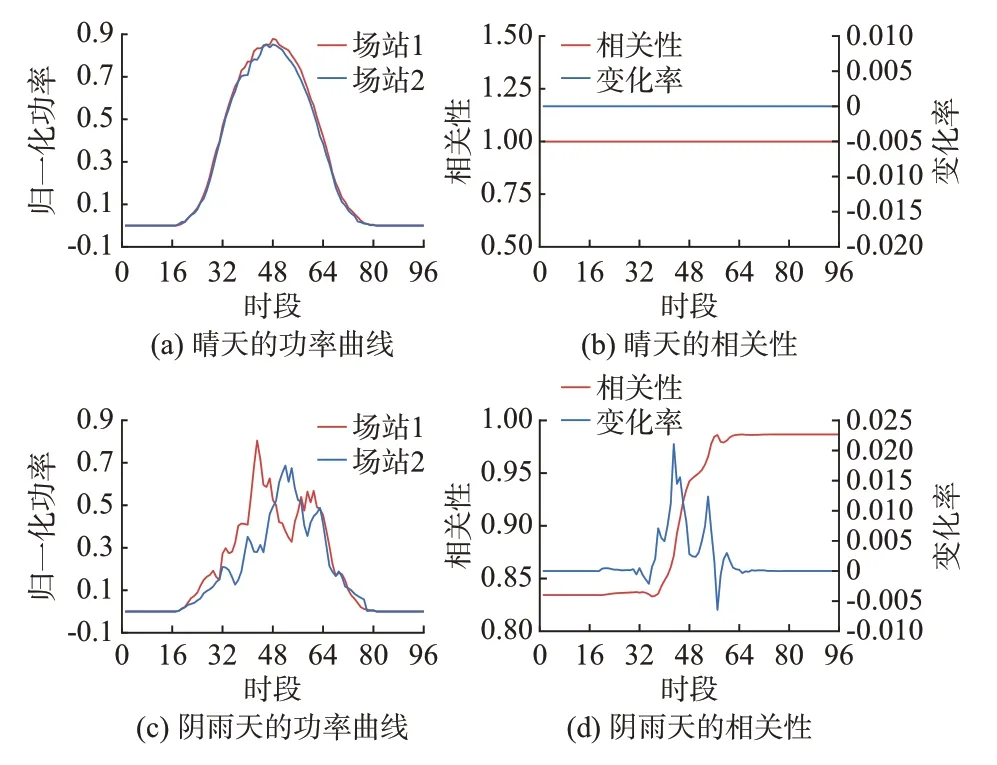
图1 分布式光伏出力相关性Fig.1 Correlation of distributed photovoltaic output

实际上，在晴朗天气下，受太阳辐射日周期性和年周期性的影响，对于位置固定的集群分布式光伏站点，其出力具有一定的确定性，这体现了场站间长期稳定关系。然而，在非晴朗天气下，受外部气象等因素变化影响，具体表现在受云团生消、位移等影响，各分布式光伏出力呈现一定程度的波动、不确定性，这体现了场站间剧烈动态变化关系。

通过对不同出力状态下场站间相关性变化情况的观察与分析可知，静态表征方式仅能反映分布式光伏场站间长期稳定关联关系，无法表征场站间短时变化关系。同时，直接对复杂的功率序列建模也增加了关联关系挖掘难度。这些因素制约了GCN特征提取性能。因此，为实现对分布式光伏时空相关性的有效、精细化表征，本文将分布式光伏出力分解为多个波动模态分量，利用各分量表征各站点间关联关系，以实现功率预测精度提升。

2 基于时空关联动态表征与GCN 建模的功率预测方法

所提基于时空关联动态表征与GCN 建模的分布式光伏超短期功率预测方法主要分为3 个步骤，整体过程如图2 所示。

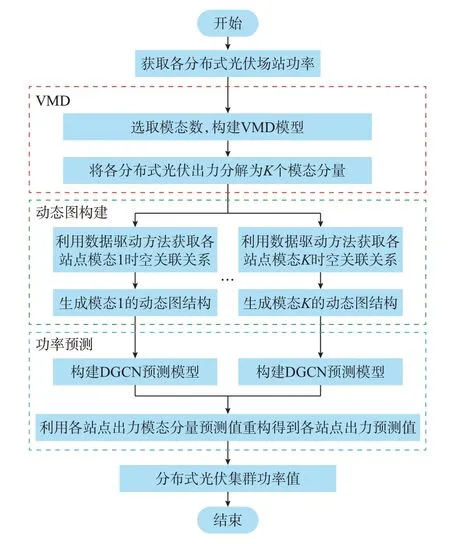
图2 所提方法框架Fig.2 Framework of proposed method

1）VMD。根据中心频率法选取合适的模态数，利用VMD 将N个分布式光伏场站功率序列[I1，I2，…，IN]分解为K个相对简单的模态序列，其中，In=[In，1，In，2，…，In，K]，n∈[1，N]，以 降 低 分 布式光伏功率的波动性，并通过对不同模态分量的针对性建模实现功率预测精度有效提升。

2）动态图构建。N个场站的模态频率近似。利用数据驱动方法，分别针对N个场站的模态k进行时空关联性的挖掘表征，以获取当前执行预测时刻t的 时 空 图 结 构 数 据Gk，t=(V，Ek，Ak.t)，k=1，2，…，K。在此基础上，将多个时空图结构堆叠，以获取动态图结构数据。

3）DGCN 功率预测。构建DGCN 功率预测模型，挖掘利用K个模态分量对应的动态图结构数据中蕴含的时空关联特征，用于得到各场站的模态子序列预测值，然后重构得到各场站功率预测值，进而得到集群功率预测值。

2.1 VMD

VMD 是一种能将原始光伏功率分解成一系列具有特定带宽的本征模态分量的非平稳信号自适应分解算法。由于具有较好的自适应能力且能够克服模态混叠现象，VMD 被用于光伏功率序列分解领域［26］。具体分解过程如下：

1）对于模态Ik，t，通过希尔伯特变换计算相关的分析信号，以便获得单向频谱。然后，与指数算子相乘，将各模态的频谱调制到相应“基带”：

式 中：δt为 单 位 冲 激 函 数；Ik，t和ωk，t分 别 为t时 刻 的第k个模态及其中心频率。

2）通过解调信号的高斯平滑度，即梯度的平方范数，来估计各个模态的带宽：

式中：pt为t时刻的分布式光伏功率；∂t为时间的微小 变 化 量；{Ik，t}和{ωk，t}分 别 为K个 模 态 与 中 心 频率的集合；||·||表示Euclid 范数。

3）引入二次惩罚因子α和拉格朗日乘子λ使式（3）变成无约束优化问题，得到其拉格朗日表达式，然后求最优解，如式（4）所示。

利用交替方向乘子法求解上述方程，该方法的基本思想为固定其余变量来更新其中一个变量。由此，得到模态、中心频率与拉格朗日乘子的求解公式为：

在满足给定的判别精度ε后停止迭代，获得最终的模态分量值如下：

最终，通过傅里叶逆变换将各模态转换到时域，得到分布式光伏功率序列分解后的K个模态分量。

2.2 动态图构建

受天气条件影响，具体表现在云团生消、位移等因素的作用下，各分布式光伏场站会呈现剧烈的出力波动，其关联关系也因此呈动态变化。这种关联关系动态变化现象在超短期预测时间尺度下更加显著，因此，仅依靠静态图结构难以实现分布式光伏间关联性有效表征。本文以数据驱动方式构建了一种时空关联表征方法，如式（9）所示。

式中：Ψ(·)为时空关联表征函数；At为t时刻邻接矩阵；In，t-σ：t为t-σ到t时段的第n个分布式光伏场站的模态，其中，σ为历史序列长度，n=1，2，…，N。

其基本原理为从时空双维度对数据建模挖掘：首先，利用全连接网络将原始节点特征映射到更高维度空间，以提取深层高维特征，并基于卷积操作沿时间轴提取各节点的深层次时域特征；然后，通过度量函数聚合相邻节点的时域特征，捕获节点间的空间依赖关系，并进一步实现时空关联性的挖掘，以获取当前执行预测时刻所对应的时空图结构数据。在此基础上，将多个时空图结构堆叠，可获取更大范围内的动态图结构数据集合。由此，利用具有动态时空相关信息的图结构集合实现对场站间动态时空关联性的表征，整体过程如图3 所示。

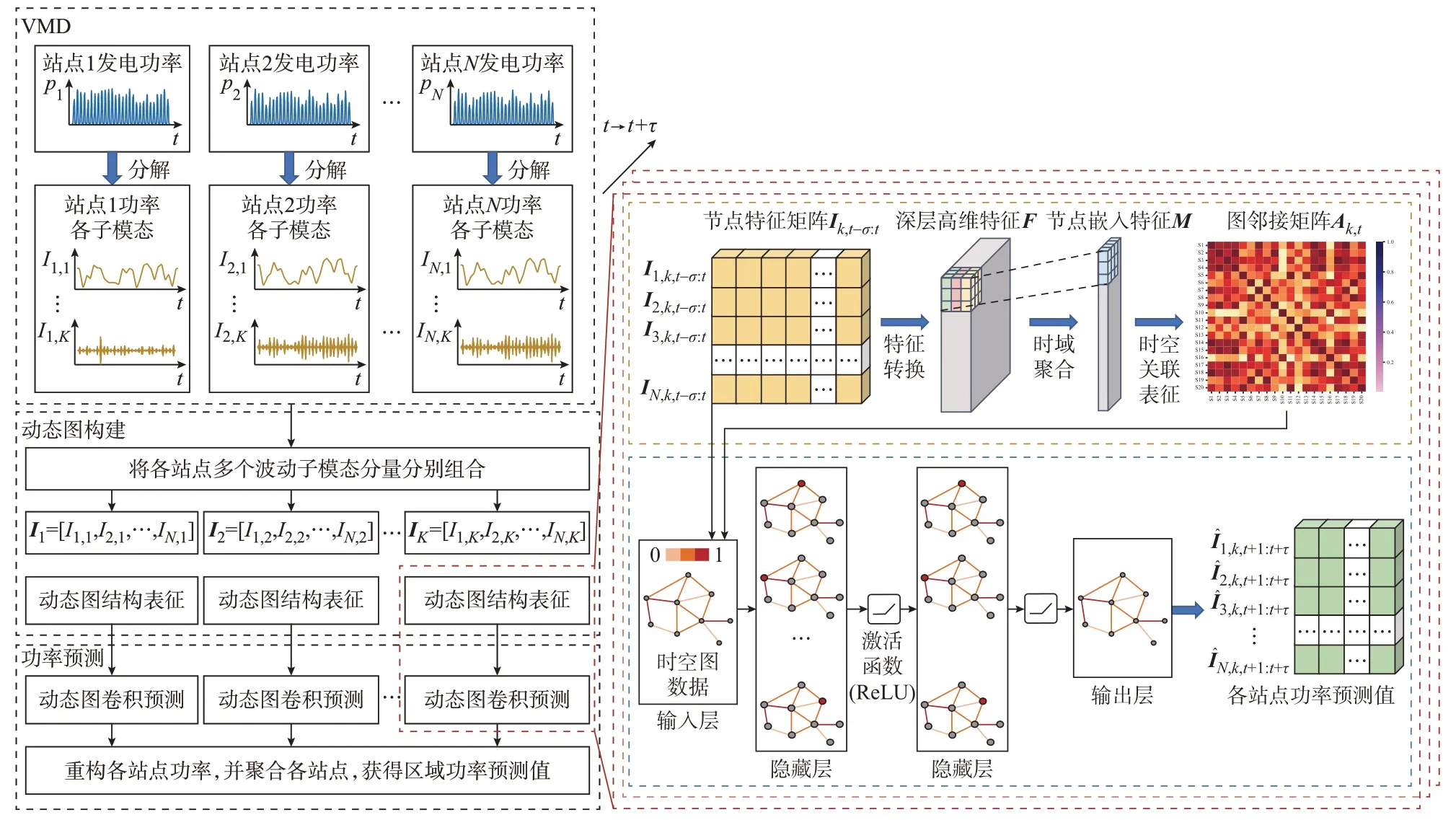
图3 时空关联动态表征与GCN 建模方法流程Fig.3 Process of spatio-temporal correlation dynamic characterization and GCN modeling method

以t时刻波动子模态分量的时空图构建为例，给定历史长度σ的节点特征矩阵Ik，t-σ：t∈RN×σ。首先，利用全连接网络fFC将原始节点特征映射到高维度空间，以提取深层高维特征F∈RN×σ×Γ，用于挖掘节点时间维度深层关联信息，如式（10）所示。

然后，为了获取[t-σ，t]时间段内节点的时间关联关系，利用大小为σ×Γ×Γ′的卷积核对节点深层特征F执行时域卷积操作，对深层特征沿时间维度进行聚合，通过训练过程中自适应调整卷积核，挖掘F对最终功率预测的贡献度，并以此实现F在时间维度与特征维度的最优聚合。由此，实现对时

2.3 区域分布式光伏功率预测

3 仿真案例

3.1 数据介绍

3.1.1 数据来源

本文实验数据来自中国河北省石家庄市的20 个分布式光伏场站的发电功率数据，总装机容量为227.84 kW，地理位置分布在东经113.93°～115.30°、北纬37.65°～38.38°之间，如附录A 图A2 所示。数据时 间跨度为2020 年7 月1 日00：00 到2021年7 月1 日23：45，时间分辨率为15 min。

3.1.2 数据预处理

首先，对原始数据集进行清洗，以削弱异常数据对功率预测模型性能的影响。由于异常数据的辨识修复不是本文的研究重点，这里的异常数据仅针对出力超过容量的异常过大值、出力为负的异常过小值和功率缺失值，数据修复通过用异常点前后3 个正常点功率的平均值代替实现。然后，将清洗后的数据按照8∶1∶1 的比例划分为训练集、验证集与测试集。划分完成后，对所有数据进行归一化处理，如式（21）所示。

3.2 评价指标

作为预测中最常用的误差指标之一，NRMSE通过平方显著增加了大偏差对最终精度的影响，其评价结果通常比NMAE 更可靠。R2用于评价实际数据与预测结果之间的相关性，但不能反映数据之间的偏差。只有当NRMSE 和NMAE 接近时，它才能更好地发挥评价作用。NWRMSE 以每个时刻误差大小在总误差中的占比作为权重，对方差进行加权求和。与NRMSE 相比，NWRMSE 进一步增加了对大误差的敏感程度，对功率预测的质量提出更严苛的要求。NMBE 用于评价预测误差的相对幅值，虽然存在误差正负抵消的问题，但与NMAE 配合使用可以评估预测值与真实值的拟合程度。综合上述5 种预测精度评价指标，对各类预测方法误差特性进行较为综合的评价。

3.3 实验设置

为证明本文方法的有效性，除本文所提方法外，设置了另外4 种方法作为对照模型：

方法1：直接以各分布式光伏出力为节点特征，利用动态GCN 建模预测，获得集群总功率。

方法2：将各分布式光伏出力进行分解，利用静态GCN 建模预测，获得集群总功率。

方法3：直接以各分布式光伏出力为节点特征，利用静态GCN 建模预测，获得集群总功率。

方法4：利用卷积神经网络（convolutional neural network，CNN）与长短期记忆（long shortterm memory，LSTM）神经网络的组合模型进行预测，即以各分布式光伏出力作为模型输入，利用CNN 挖掘各场站空间关联性，然后利用LSTM 神经网络挖掘时间关联性，获得集群总功率。

方法5：利用LSTM 模型预测各分布式光伏场站出力，然后累加获得集群总出力。

本文实验利用Python 与MATLAB，仿真设备硬件配置为Intel Core i9-9900X 3.50 GHz CPU，64 GB RAM， NVIDIA GeForce GTX 2080Ti GPU。

3.4 结果分析

3.4.1 功率分解结果

VMD 的分解效果主要受模态数K的影响，通过对不同模态数下中心频率的分布进行观察可选取合适的K值。本文将所有分布式光伏站点作为图结构中的图节点，将不同频率下的模态信号作为节点特征。因此，所提方法需要各个场站尽量获得同等数量的模态。为保证各场站模态数相同且集群总功率预测值最优，本文计算各个分布式光伏场站与集群总出力的相关性，选取最大相关性的场站作为代表性场站进行模态数的选取，其中，相关性利用皮尔逊系数表征。结果见附录B 表B1。可见，当K=11时，模态9 与模态10 中心频率相差不到25%，因此选取K为10。代表性场站分解结果见附录B 图B1。

3.4.2 功率预测结果

各方法预测精度评价指标如表1 至表5 及附录C 图C1 所示，评价指标统计尺度为全测试集样本。可以看出，本文所提方法在绝大多数评价指标上均优于其他方法。同时，基于GCN 的4 种方法（本文方法、方法1、方法2、方法3）均优于传统的CNN 与LSTM 预测方法，且考虑时空关联性的预测方法（本文方法、方法1、方法2、方法3、方法4）均优于未考虑时空关联性的预测方法5。考虑动态时空关联性的方法1 预测性能优于考虑静态时空关联性的方法2 与3，且相较于方法2 与3 在提前15 min 与4 h 预测结果的eNRMSE值上分别提升了13.4% 与2.4%、18.9%与6.9%。原因是方法2 仅依靠将复杂的分布式光伏出力时间序列分解为多模态子系列，虽在一定程度上降低了时空关联特征的挖掘难度，但难以对分布式光伏间动态时空关联性进行有效表征，因此，无法充分发挥图卷积网络的时空特征挖掘能力，预测精度提升有限。而与之相比，方法1 利用数据驱动方式对分布式光伏间深层次时空关联性进行动态表征，且其表征方式在训练过程中不断迭代更新。在此基础上，本文方法引入分解机制后，进一步提升了预测效果。可见，将复杂的分布式光伏出力序列分解为多个模态分量再分别建模预测的方式，能有效简化出力序列，降低分布式光伏间关联性挖掘难度，实现精度提升，使eNRMSE值在提前15 min 与4 h 时间尺度上分别提升了5.2% 与4.8%。由于eNWRMSE增加了大误差在最终误差指标的权重，各方法的eNWRMSE指标均高于eNRMSE指标。本文方法具有更小的eNWRMSE指标，这说明与其他方法相比，本文方法预测误差更平稳，较大误差发生情况少。虽然在某些预测尺度下本文方法的eNMBE指标差于其他方法，但结合eNMAE来看，是其他方法正负误差抵消导致的，这更能说明本文方法预测偏差小、分布集中。

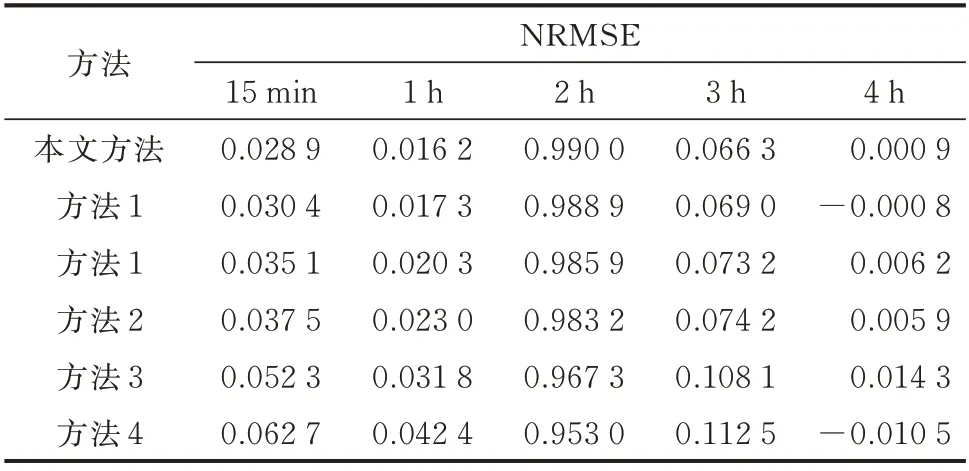
表1 预测结果的NRMSE 指标Table 1 NRMSE indices of forecasting results

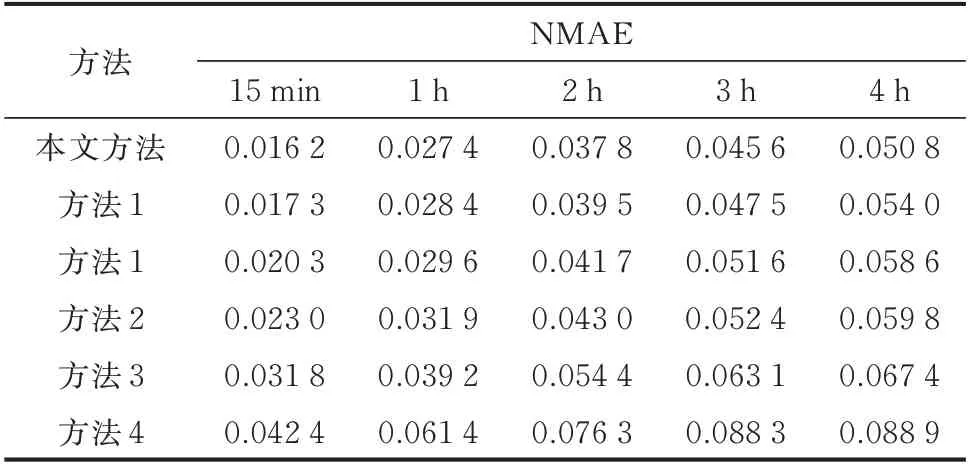
表2 预测结果的NMAE 指标Table 2 NMAE indices of forecasting results

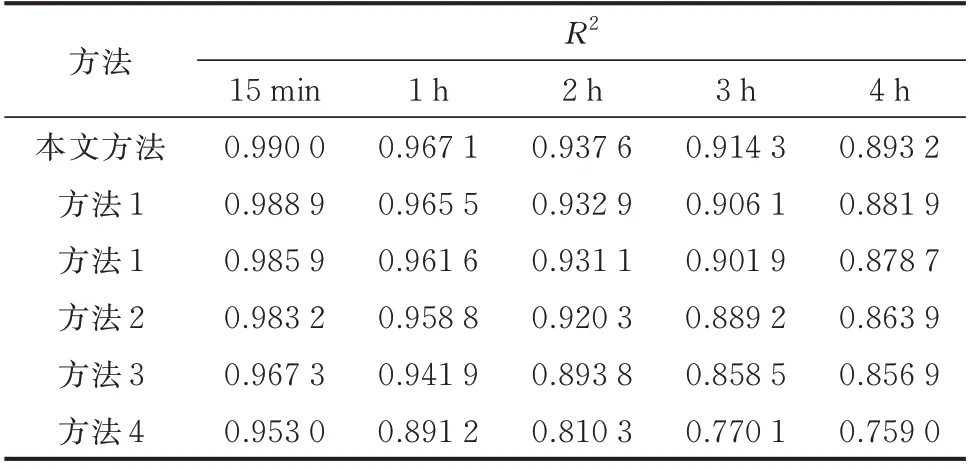
表3 预测结果的R2指标Table 3 R2 indices of forecasting results

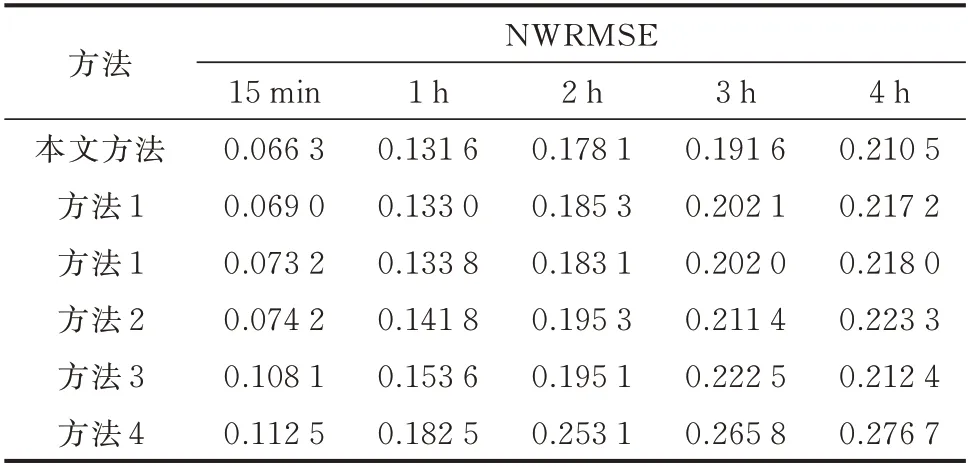
表4 预测结果的NWRMSE 指标Table 4 NWRMSE indices of forecasting results

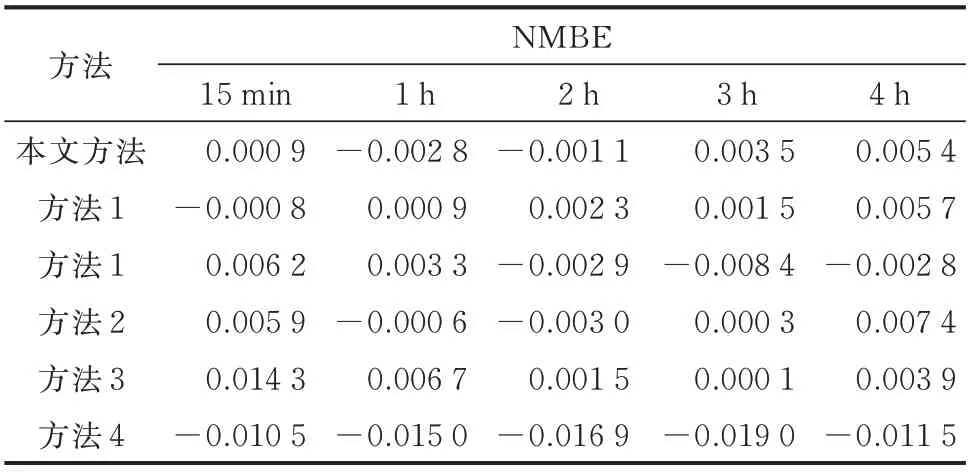
表5 预测结果的NMBE 指标Table 5 NMBE indices of forecasting results

4 种基于GCN 的预测方法连续5 d 的预测结果如附录C 图C2 所示。方法3 利用GCN，通过构建图结构数据实现各节点间关系的表征，克服了方法4不能表征场站间相互影响程度强弱的缺陷。在此基础上，方法2 通过将原始功率序列分解为多个模态分量并针对性建模，预测效果取得了一定提升。方法1 在各时刻自主挖掘、动态表征各站点间的关联关系，其预测结果偏离实际值的程度相较于方法2、3 得到了缓解，这种现象在提前2 h 和4 h 的预测曲线中更为明显。进一步地，本文方法利用多个模态序列，从不同维度表征光伏出力波动特性，并通过针对性建模取得了更好的预测效果。此外，可以看出在出力相对稳定时，4 种基于GCN 的方法均能取得不错的预测效果；但当出力剧烈波动时，方法2 采用对复杂功率序列分解并针对性建模的方式改善了方法3 直接建模的预测效果。然而，由于其仅考虑长期关联关系，难以反映由于出力短时波动带来的关联性动态变化，预测效果提升有限。同时，直接利用功率序列挖掘动态关联关系的方法1 虽取得一定效果，但由于功率序列短时波动剧烈、模式复杂，制约了关联性的有效挖掘，其拟合效果差于本文方法。

在较短预测尺度上，本文方法较好地拟合实际出力曲线。而在长期尺度上，特别是在4 h，虽然本文方法可达到较好的预测精度指标，但对实际出力的拟合效果并不理想。尽管如此，仍可看出本文方法比起其他方法有更好的拟合效果。未来，将进一步增强本文方法长期相关性的挖掘能力，以提升在长预测尺度上的拟合效果。

为进一步说明本文方法的有效性，对各个方法在晴天、多云、阴雨、暴雨4 种典型天气场景［29］下提前4 h 的预测效果进行了比较，如图4 所示，各类天气下的精度指标统计结果见附录C 图C3。可以看出，本文方法在4 种天气类型下均表现出更准确的预测精度，相较于其他方法在非晴天气下功率预测精度均有一定程度的提升。同时，本文方法的预测功率与实际功率变化趋势更接近，预测误差较小。这说明在经过功率分解后，有针对性地建模挖掘同模态下各场动态关联关系，能实现多维信息的挖掘，有效提升功率预测精度。方法1 预测效果虽差于本文方法，但通过考虑各站点间动态关系关联以提升GCN 特征挖掘效果，也在非晴天气下取得了不错的预测效果，且较大程度上缓解了以静态关联性作为输入的方法2 与3 预测结果与实际功率偏离较大的问题。这说明动态时空关联性信息不仅可以帮助GCN 掌握分布式光伏集群功率的变化趋势，还可以有效缓解由于非晴天气下分布式光伏出力剧烈波动造成的预测曲线与实际值偏差过大的问题。因此，对动态关联关系的表征对提高光伏功率预测精度具有重要意义。尤其是在数值天气预报缺失的情况下，从邻近分布式光伏功率序列中充分挖掘出力变化的规律特征，能为各电站出力预测提供更多的有利信息。

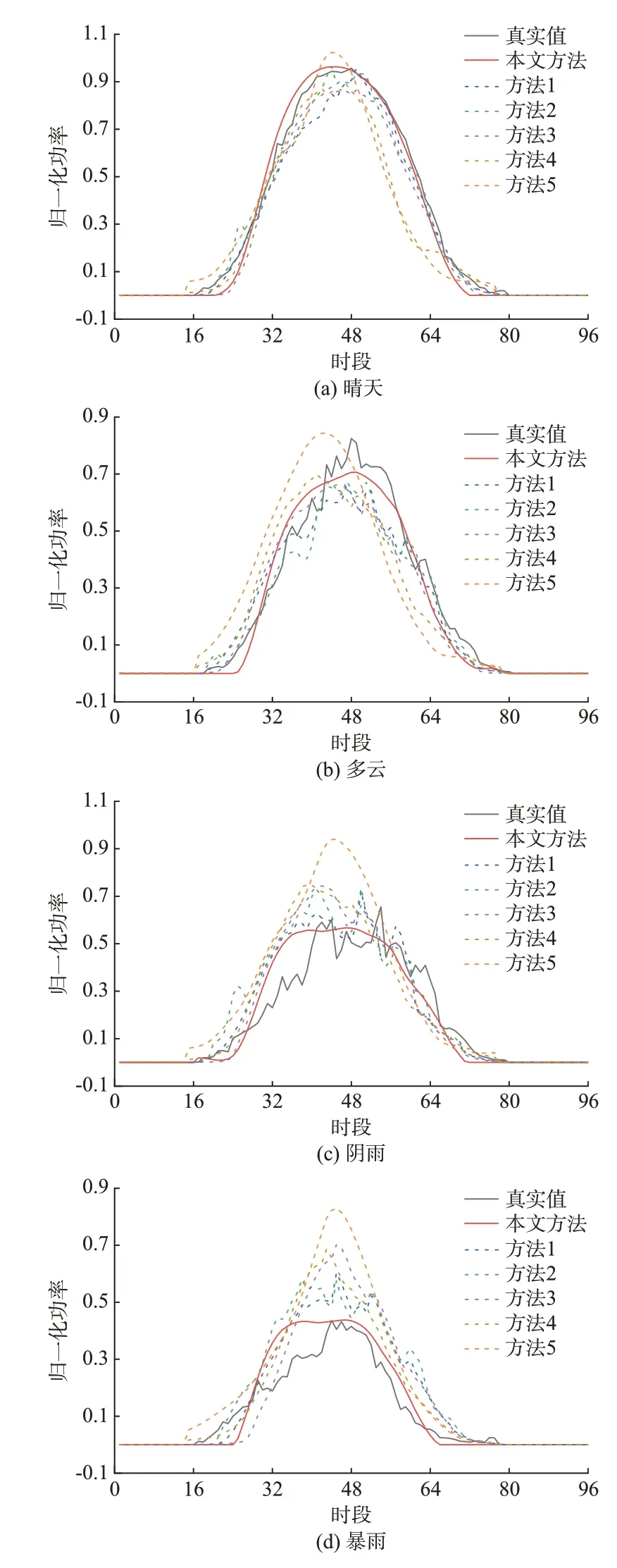
图4 不同天气类型下提前4 hours 的预测结果Fig.4 Forecasting results of 4 hours in advance under different weather types

基于GCN 的预测模型可以实现各节点的功率预测。为验证各类方法在不同分布式光伏场站的适应性，将各种方法在各站点下的预测精度进行了计算，各节点的eNRMSE如图5 所示。可以看出，15 min时间尺度下预测精度数值分布较分散，1 h、2 h 下预测精度分布反而集中。这种情况的出现可能是由于有些场站短时间内出力波动不大，较长时间尺度来看波动剧烈，有些场站则一直呈现剧烈波动。随着预测时间尺度的增加，各站点功率预测精度均呈现下降趋势。在短时间尺度下，某些场站出力较稳定，功率预测精度较高；某些场站出力波动剧烈，功率预测精度较低，因而预测精度数值较分散。在较长时间尺度下，各场站出力不确定性更强，因而精度都较低。15 min 时间尺度下预测精度数值虽然较为分散，但相比于其他时间尺度下预测精度均相对较高。此外，如附录C 图C4 所示，本文方法在各分布式光伏均可取得较好的预测效果，在预测精度和模型适应性方面具有较好表现。图5（c）和（d）表明，与其他GCN 预测方法相比，本文方法在捕获功率的长期时间依赖性方面也具有一定的优势。

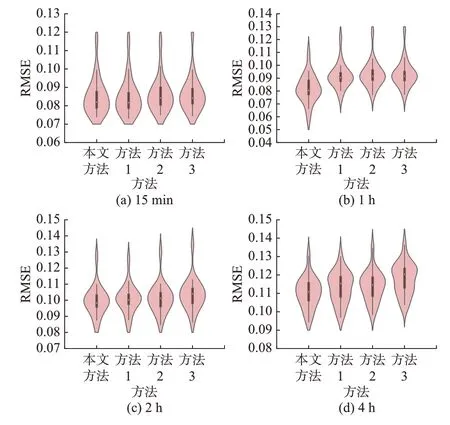
图5 不同时间尺度下各场站预测精度分布Fig.5 Distribution of forecasting accuracy of each site at different time scales

4 结语

准确的分布式光伏功率预测为有源配电网运行管理、调度运行、分布式新能源消纳等起到关键支撑作用，对于有源配电网安全稳定运行具有重要意义。为此，本文提出了一种基于时空关联动态表征与GCN 建模的分布式光伏超短期功率预测方法，所得结论如下：

1）利用VMD 将复杂的分布式光伏出力序列分解为多个波动较小、模式简单的子序列，可以有效降低各场站关联关系挖掘难度，提高功率预测精度。

2）利用动态时空关联性表征方法，挖掘节点特征中的相关信息来描述突发波动，可实现节点间动态短时关联关系的有效表征，用以提升GCN 的时空特征挖掘效果，实现功率预测精度的有效提升。

3）利用动态邻接矩阵构建方法，将传统GCN 模型改进为了DGCN，实现了功率预测精度的有效提升。仿真结果表明，与静态图卷积预测效果相比，所提方法在4 h 时间尺度的预测精度可以获得11.4%的提升。在不同天气类型下均能获得理想的集群预测效果，并且在各场站的出力预测中均表现出良好的预测性能，具备优越的适应性和预测性能。

值得注意的是，本文方法在较长预测尺度上对真实功率的拟合效果较差，一方面是由于模型挖掘长时间依赖性的能力不足，另一方面是信息源较少。为此，未来将引入多源卫星遥感信息［30-31］、改进算法提升其长期相关性挖掘能力，以进一步提升功率预测精度。

本文研究得到新型电力系统运行与控制全国重点实验室开放基金课题(SKLD22KM1 4)资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。