水平砂垫层加速城市固体废弃物降解固结理论研究

李艳梅，梅国雄,2，田乙，吴文兵,2，徐美娟

(1.中国地质大学 工程学院，湖北 武汉，430074；2.浙江大学 海洋学院，浙江 舟山，316021；3.浙大城市学院 土木工程系，浙江 杭州，310015)

近年来，城市生活垃圾产生量迅速增加，引发了严重的环境问题。我国城市固体废弃物(municipal solid waste，MSW)中厨余垃圾含量高，具有压缩性强、易降解的特点，其变形和沉降是卫生填埋场的主要岩土问题之一[1]。设计填埋场的填埋量时，需要准确预测填埋体沉降量。填埋场关闭后，沉降过快或过多会影响填埋体的稳定性[2]，从而造成不同程度的工程事故以及环境污染问题。因此，研究MSW降解固结计算理论在填埋场工程设计中至关重要[3]。

与土体类似的是，MSW 也存在成层性的特点。谢康和等[4-7]通过理论推导，得到双层土的一维固结解答和热固结解答。但是，正常土体骨架不会压缩，而MSW 以可压缩的有机物充当骨架，且MSW 本身组分也可压缩，这使MSW 具有不同于正常土体的压缩性。学者们提出了几种预测城市生活垃圾沉降的模型，包括土力学压缩理论模型[8-9]、经验模型、流变蠕变模型[10]和生物降解类模型[11-12]。结合CHEN 等[13]的一维压缩模型、VAVILIN 等[14]的一阶水解动力学模型、POWRIE等[15]的渗透系数计算模型，陈云敏等[16]推导出了考虑可降解固体水解、胞内水释放为孔隙水及降解导致压缩性衰变的简化一维固结模型。其中，一维压缩模型将应变分解为主应变和次应变2个部分，分别由渗流固结和生物降解产生，主应变和次应变相加形成最终总应变。

在填埋体的辅助处理手段中，加设排水体是处理导排系统淤堵和加速排水固结的有效方法。近年来，固结排水理论的研究多与竖向排水体有关，如铺设塑料排水板[17-18]、砂井[19-20]、透水管桩[21-22]、预制排水管[23]等；而对水平排水体如砂垫层[24-25]、水平塑料排水板[26]、土工布等的研究仍不足。冯健雪等[27-29]研究了单、双层地基水平砂垫层位置及砂垫层几何物理参数对地基固结速率的影响。目前，针对MSW固结的研究主要集中在机理方面，对如何提高固结速率的研究相对较少。由于垃圾填埋场是分层填埋的，相比于竖向排水体，在MSW中铺设水平排水砂垫层不仅易于施工，而且能够有效缩短排水路径长度，从而提高MSW固结速率，但相关理论仍有待研究，以满足工程设计需求。

本文针对水平砂垫层加速城市固体废弃物降解固结问题展开研究。首先，建立双层MSW一维降解固结模型，旨在探究不同排水边界条件下的砂垫层最优铺设位置的分布规律。其次，采用连续排水边界模拟底部导排层的排水情况，考虑水平砂垫层的铺设，从而搭建双层MSW一维降解固结控制方程。再次，结合有限元软件COMSOL Multiphysics 的PDE 模块，得到相应的数值解答。最后，对参数进行分析，深入探究双层MSW的一维降解固结特性，以便为工程设计中水平砂垫层的位置优化提供理论依据。

1 模型建立

1.1 问题描述

城市生活垃圾填埋场结构如图1所示。填埋体边界具有不同的排水能力，因此，传统一维固结理论中将排水边界视为完全透水或完全不透水都不准确[30]。梅国雄等[31]提出了更贴近工程实际的连续排水边界。研究表明[32-35]，连续排水边界比透水或不透水边界更适用于实际工程情况。因此，在本研究中将MSW顶面边界视为不排水边界，水平砂垫层视为完全排水边界，底面导排层视为连续排水边界。计算示意图如图2所示。图2中，Hj为第j层的层厚度；kwj为第j层的渗透系数；mvj为第j层的体积压缩系数；Esj为第j层的压缩模量；CVj为第j层的固结系数；ui为各部分孔压(j=1，2，表示原两层MSW 的层数；i=1，2，3，表示铺设水平砂垫层后被分为三层的MSW层数)；h为水平砂垫层铺设深度；p为瞬时荷载。

图1 城市生活垃圾填埋场示意图Fig.1 Schematic diagram of municipal solid waste landfill site

图2 铺设水平砂垫层双层MSW降解固结模型示意图Fig.2 Schematic diagram of degradation consolidation model for double-layer MSW with horizontal sand blanket

1.2 假设条件

模型中采用如下假设：

1)MSW 均质且完全饱和，固相颗粒和孔隙水、胞内水不可压缩；变形由孔隙水排出和固相水解导致，变形是小变形，不考虑热固耦合作用。

2)孔隙水渗流服从达西定律，渗透系数由经验公式kw=0.2/[σ′(z，t)]3确定。

3)胞内水、孔隙水密度相同，忽略固相溶解引起的孔隙水体积变化。

4)忽略降解对先期固结压力的影响，计算初始时刻尚未发生次应变。

5)先期固结压力沿深度均匀分布，且假设荷载p为瞬时均布荷载。

1.3 控制方程

根据陈云敏等[16]的一维压缩固结模型，新鲜固体废弃物的应力与应变满足关系：

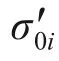
生物降解服从式(3)所示的水解一阶动力学模型[14]：

式中：msdi和mswi分别为第i层剩余可降解固相和胞内水质量；msd0i和msw0i分别为第i层单位体积内的可降解固相和胞内水的质量；fmsi和fmwi分别为第i层可降解固相的水解程度和胞内水释放程度；csi和cwi分别为第i层可降解固相水解速率和胞内水释放速率。

根据有效应力原理，随着孔压消散，深度z处有效应力σ′i(z，t)=σ′ci+p-ui(z，t)。考虑次应变受可降解固相水解影响，采用可降解组分质量损失程度Umi描述次应变完成程度Uci，ci为第i层次应变速率系数：

结合一维压缩固结模型、水解一阶动力学模型以及达西定律，得到控制方程为

式中：fi(z，t)为降解导致的源汇项，其作用效果等同于施加随时间变化的荷载fi(z，t)，

固结系数CVi(z，t)为

1.4 定解条件

设初始荷载为瞬时均布荷载，水平砂垫层铺设深度为h。为方便讨论，设h/H=β。连续排水边界界面参数为α。初始条件为

根据前面假设，顶面、底面和砂垫层处边界条件为：

层间连续条件为：

2 固结解答

2.1 数值解答

经以上推导得到非齐次非线性控制方程，该方程的求解较复杂，本文借助有限元软件COMSOL Multiphysics，通过数值方法对其进行求解。COMSOL Multiphysics软件具有强大的多物理场仿真建模能力，能够方便、快捷、正确地对多物理场耦合问题进行求解。这里使用其“数学接口” PDE 模块求解数值解。通过建立模型、添加变量、定义系数、设置边界条件、计算、输出结果，对双层MSW 一维降解固结控制方程进行求解，得到数值解。

2.2 简化解析解

本节对固结过程中压缩性和渗透性的非线性变化进行简化，并求得相应解析解。假设如下：

1)降解固结期间MSW压缩性质和渗透性质不随孔压消散和有效应力变化而变化，根据初始有效应力状态取值。

2)不考虑最终次应变受有效应力变化的影响，最终次应变按初始状态取值。

3)忽略蠕变作用，次应变速率由胞内水释放速率控制。

总应变与应力满足关系：

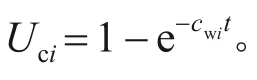
源项为

控制方程为

2.3 孔压解答

当水平砂垫层铺设在上层MSW 即0 ＜h＜H1时，孔压记作uu(z，t)，对水平砂垫层上部MSW，将定解条件式(10)和(11)齐次化，令V1(z，t)=uu1(z，t)-pe-t(h2-z2)/h2，则uu1(z，t)=V1(z，t)+pe-t(h2-z2)/h2，F1(t)=f1(t)+pe-t(h2-z2+2)/h2，得到齐次定解条件下的线性非齐次二阶偏微分方程：

用分离变量法求解式(21)得到

同理，可得到水平砂垫层下部MSW的固结方程。设

则Fi(t)=fi(t)+αpe-αt(h-z)/(h-H)，得到方程组：

采用分离变量法，可得式(24)的解为

其中：

Am1、Bm1、Cm1和λm1为待定系数。将式(25)和(26)代入到层间连续条件式(12)中，解得

式(28)是确定λm1的特征方程。将式(25)代入式(24)中，得到：

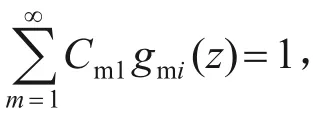
解得：

由边界条件可得到：

因此，Bm1=0。将Am1、Bm1、Cm1、βm1、λm1和Tm1代入式(23)和式(25)可得到MSW孔压为：

当水平砂垫层铺设在下层MSW中即H1＜h＜H时，孔压记作ud(z，t)，与前文同理，根据分离变量法求解得水平砂垫层上部MSW孔压：

对于水平砂垫层下部MSW，令A2=∫eCV3λ2t f3(t)dt，求解得

2.4 固结度解答

对于降解固结，以孔压定义的固结度Up与以沉降定义的固结度Us是不相同的。按孔压定义的固结度Up表达式为

根据式(1)所示应力与应变关系，得到最终应变为

按沉降定义的固结度Us表达式为

2.5 解答验证

在COMSOL Multiphysics 数值模型中，按照2.2 节中的简化方式对模型中的有效应力和次应变速率系数进行简化，得到简化模型数值解。图3所示为α=0.5 d-1时水平砂垫层铺设于MSW顶部的孔压数值解与解析解对比结果，从图3 可见：2 条曲线基本重合，这验证了解析解的正确性。

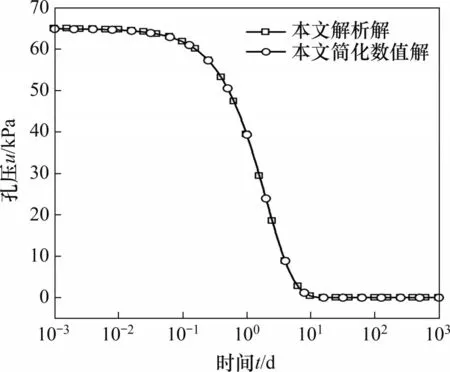
图3 本文简化模型解析解与数值解的比较Fig.3 Comparison between analytical and numerical solutions of simplified model

当水平砂垫层铺设于顶部即h=0时，可认为边界条件为双面排水，顶部边界为太沙基完全排水边界。当k=b=1，可得到μ=1，则CV1=CV2，双层MSW 变成均质MSW 问题，此时根据式(28)，可得到：

将式(43)代入式(32)，因为当m为偶数时，Cm1=0，令M=(2m-1)π/2，则Cm1=2/M。孔压解答式(34)和式(35)可以简化为：

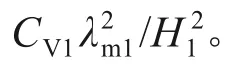
根据连续排水边界定义，界面参数α可描述边界排水能力。当界面参数α趋于无穷大时，连续排水边界退化为太沙基完全排水边界，在此基础上不考虑降解作用，即式(19)所示的降解源项f(t)为0，可得到：

所得孔压解答形式与太沙基完全排水边界下的饱和土体一维固结解答一致，可以看作厚度为(H1+μH2)的均质单层饱和土体固结问题，这进一步验证了本文解答的合理性。

3 界面参数α 对MSW 降解固结的影响

不考虑水平砂垫层厚度和渗透系数的影响，借助数值软件COMSOL Multiphysics 的PDE 模块求得数值解，分析单个填埋体固结特性，讨论连续排水边界界面参数对MSW降解固结特性的影响及水平砂垫层最优铺设位置。结合苏州七子山填埋场实验数据[36]，取e0=4.2，σ′0i=5.5 kPa，整理典型MSW参数，得到表1，并将其代入2.3节的公式中进行计算。

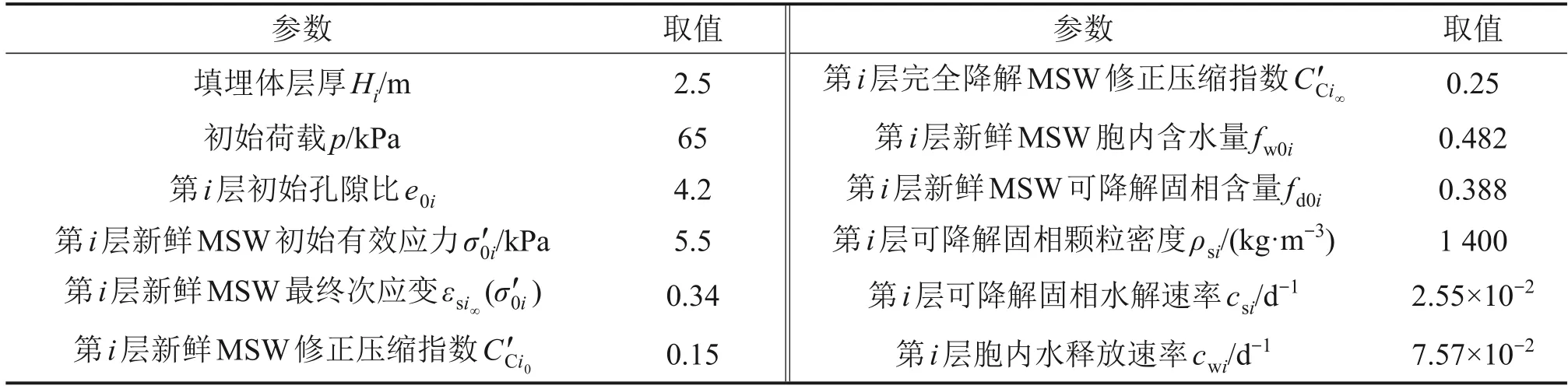
表1 我国典型MSW基本参数Table 1 Basic parameters of typical MSW in China

为分析排水条件对加砂垫层MSW降解固结特性的影响，考虑实际工程铺设习惯，将水平砂垫层铺设于上层填埋体中间位置(即β=0.25)。为了表示边界排水能力从弱至强的变化，对界面参数α分别取0.1、0.5、5、50 和300 d-1，讨论底面不透水时MSW降解固结特性。

图4所示为界面参数α对MSW 降解固结特性的影响。从图4(a)可见：根据边界定义，孔压在水平排水砂垫层处为0 kPa，因此，本文中MSW 顶部的孔压随时间消散几乎不受界面参数的影响。为了讨论界面参数对孔压的影响，选取0.75H处(下层填埋体中部)孔压进行讨论。当底面为连续排水界面时，界面参数α增大，界面排水能力增强，孔压消散速率随之加快；当底面为不透水边界时，孔压消散被抑制，此时，孔压会略大于当界面参数α较小(α=0.1 d-1)时的孔压，孔压消散速率也略慢，不过最终都消散为0。

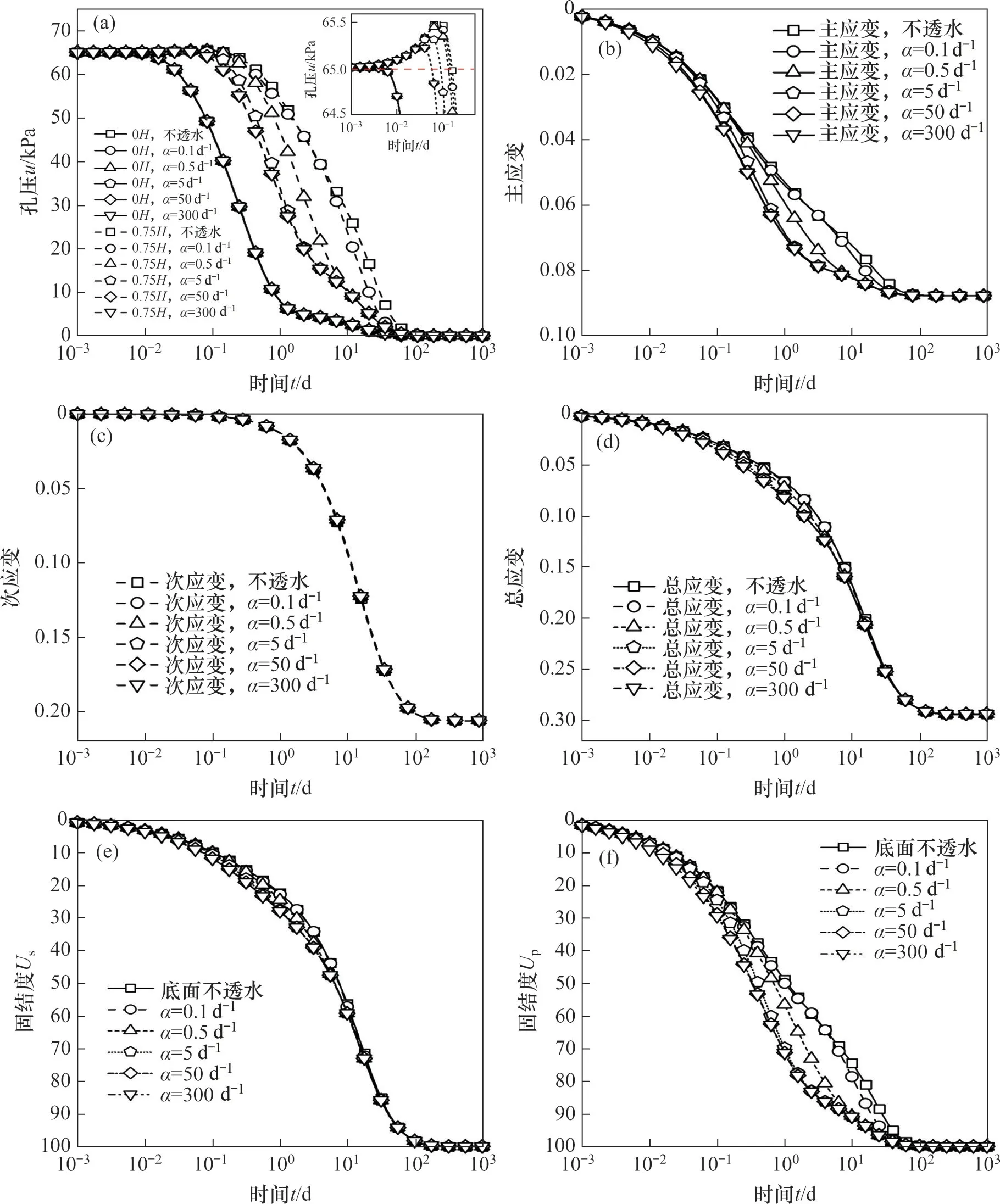
图4 界面参数α对MSW降解固结的影响Fig.4 Influence of interface parameters αon degradation and consolidation of MSW

在前期固结阶段均出现孔压大于初始荷载的情况，这是降解固结的特点之一，这是因为在前期固结阶段，MSW中固相发生水解以及胞内水释放，导致MSW压缩性增大，进而孔压增大，并且增大量大于固相质量损失导致的孔压减小量。随着固结进程发展，此现象逐渐缓解。

从图4(b)～4(d)可见：次应变由固相水解产生，MSW先期固结应力相同，因此，边界排水能力的改变几乎不影响次应变曲线的发展，且最终次应变均为0.21。主应变的变化由应力状态改变导致，受边界排水能力影响较明显。当边界是连续排水边界时，随着界面参数α增大，孔压消散速率加快，主应变发展进程随之加快；当底面不透水时，主应变发展速率小于底面排水情况下的应变发展速率，但最终主应变均为0.08。对于总应变的变化，在数值方面主要受次应变的影响；在随边界排水条件的变化方面，主要受主应变的影响，当界面参数α较大时，总应变的发展速率也更大，最终发展至0.29。

从图4(e)～4(f)可见：固结度Us主要反映了沉降完成程度，因为总应变与最终应变始终为正，所以固结度Us始终大于0。当边界是连续排水边界时，随着边界排水能力提高，固结度Us发展速率加快，同时，界面参数α越大，固结度越高，在固结前期对比更加明显。固结度Up主要反映了孔压消散程度。在固结前期，因为砂垫层处孔压为0 kPa，抵消了由于降解过程带来的孔压反向增大现象，所以，固结度Up始终大于0。与孔压发展规律类似，当底面为连续排水界面时，界面参数α增大，固结度发展进程加快；当底面为不透水边界时，受孔压的影响，固结度Up的发展速率降低，在同时刻下要低于排水边界的固结度Up发展程度。

4 水平砂垫层位置优化设计

传统水平排水砂垫层的铺设多选择在填埋体中间位置或者沿深度等距铺设。为了使孔压消散速率最大，水平排水砂垫层的铺设位置宜设置在填埋体不排水对称面上，但是不排水对称面的位置随着固结进程而变化。因此，传统铺设位置的选择不一定能最大限度地提高固结效率。对于确定工期的MSW，其时间确定时，总有一个砂垫层铺设位置使固结度达到最大值，在数学表达上当∂U/∂β=0时，固结度U取得最大值，对应的β即为此时水平砂垫层的最优铺设位置。为探究水平砂垫层的铺设规律，这里取μ=1、k=1，借助软件COMSOL Multiphysics计算，得到水平排水砂垫层在不同界面参数及时间下最优铺设位置。

图5所示为砂垫层最优铺设位置随时间变化曲线。从图5可见：水平排水砂垫层最优铺设位置随时间发展而变化，2条曲线变化规律基本一致。在相同时刻，边界排水能力逐渐变弱的情况下，其水平砂垫层最优铺设位置逐渐下移，其中，考虑固结度Up的曲线较考虑固结度Us的曲线位置略靠下。

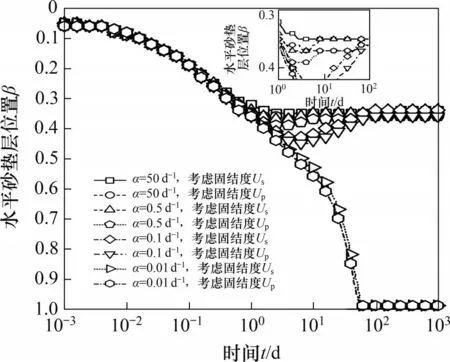
图5 砂垫层最优铺设位置随时间变化曲线Fig.5 Variation in optimal laying position of sand blanket with time

1)在固结初期，水平砂垫层最优铺设位置靠近上层固体废弃物层顶面，随着固结进度发展而逐渐下移。

2)在固结中期，当边界排水能力极弱(α=0.01 d-1)时，水平砂垫层最优铺设位置逐渐下移至接近下底面，以改善边界排水情况；当边界排水能力变强时，水平砂垫层最优铺设位置随着固结进程发展而下移至一定深度后，继续上移至一定深度，且铺设深度主要集中在上层固体废弃物中。这是由于上顶面为不排水边界，当底面排水能力逐渐变强时，靠近底面的排水条件得到改善，而靠近顶面的排水依然困难，因此，砂垫层铺设位置上移。

3)在固结后期，降解固结完成程度较高，砂垫层最优铺设位置保持不变。

堆载排水固结法中常用固结度达到85%～90%作为卸载的标准。因此，将固结度达到90%作为标准，考虑到实际工程中底面导排系统易受渗滤液等的影响而排水能力降低，这里取界面参数α=0.5 d-1。

图6所示为水平砂垫层铺设在不同位置时的MSW 固结度曲线，从图6(a)可见：β=0.35 是固结度Us达到90%时对应的最优铺设位置。在固结度Us达到10%之前，砂垫层铺设在0.1H(β=0.1)处MSW固结最快，在固结度Us达到10%之后，砂垫层铺设在最优位置(β=0.35)处MSW 固结最快。当β=0.10、0.35、0.50、0.70、0.90 时，固结度Us达到90%的时间分别为41、40、41、42和44 d。

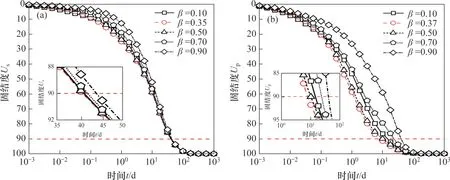
图6 水平砂垫层铺设在不同位置时的MSW固结度曲线Fig.6 Consolidation curves of MSW with sand blanket laid at different positions

β=0.37 是固结度Up达到90%时对应的最优铺设位置。从图6(b)可见：铺设砂垫层对孔压消散影响大于对应变发展的影响。β=0.10、0.37、0.50、0.70、0.90时固结度Up达到90%的时间分别为16、7、10、25和40 d。由此可见，合理铺设水平砂垫层对加速MSW排水固结具有显著作用。

5 结 论

1)考虑MSW降解固结中的渗流—降解—压缩耦合作用，修正对次应变速率系数，建立了双层MSW一维降解固结模型，其解答更具普遍性，且反映了有效应力变化对降解固结特性的影响。连续排水边界的设置反映了边界排水能力的变化，使得本文解答能够更真实反映MSW 的边界排水情况。

2)孔压、应变和固结度随着界面参数的变化而呈现非线性变化。界面参数增大，边界排水能力增强，对孔压消散速率、应变发展速率和固结度发展速率有着正面的影响。次应变由固相水解产生，改变界面参数对次应变发展的影响极微弱。

3)水平砂垫层的铺设改变了降解固结过程中孔隙水的排出路径，加速了孔压消散和应变发展。水平砂垫层的位置设置对固结度Us的影响弱于对固结度Up的影响；水平砂垫层的最优铺设位置随着界面参数和时间的变化而变化；当时间一定时，随着界面参数增大，最优铺设位置上移；当水平砂垫层设置在最优铺设位置时，与铺设在其他位置相比，可以大幅度提高MSW降解固结效率。