基于能量最小原则的高铁填料压实过程振动参数优化
2023-10-30陈晓斌谢康尧俊凯惠潇涵王业顺邓志兴
陈晓斌,谢康,尧俊凯,惠潇涵,王业顺,邓志兴
(1.中南大学 土木工程学院,湖南 长沙,410083;2.中南大学 教育部重载铁路工程结构重点实验室,湖南 长沙,410083;3.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京,100081;4.中国铁路广州局集团公司,广东 广州,510440)
为了保证高铁路基的安全性并提高列车运行的舒适性,对路基填料的级配、最大粒径、形状均有着严格的标准[1-3]。相比于堆石坝、公路的填料选取,高铁填料填筑时需要沿线设立填料厂,从而保证高铁填料质量[3]。传统的高铁路基振动压实质量检测一般采用试坑取样法,分别对采用静压、弱振、强振等振动参数下的压实结果进行抽样检测[4]。然而,该方法忽略了填料离散性问题,导致压实效率低、压实不均匀等问题。
压实过程控制是近期研究的热点,学者们提出了许多理论和技术,并将其应用于压实过程控制[5-8],主要包括连续压实控制(continuous compaction control,CCC)和智能压实(intelligent compaction,IC)。CCC 是指在振动压实过程中,基于机土耦合相互作用原理处理振动轮竖向振动信号,建立压实质量控制体系[9]。虽然CCC 已在铁路建设中得到广泛应用,但是仍然存在缺陷,主要表现在缺少对压实过程中振动参数的改进研究[10]。填料压实状态会随着压实过程不断发生变化,根据填料压实状态不断调整振动参数,而不是采用固定的压实参数。国外将CCC 与压路机振动工艺参数调节功能结合起来,又被称作“智能压实(IC)”[9-10]。在振动过程中,如何调整振动参数一般由驾驶员操作来实现,其本质上属于人工控制的范畴。智能压实则是在没有人员参与的情况下,利用压路机的自动调节控制装置,基于填料的压实状态自动调整振动参数。目前,智能压实很难到达自动调参的功能,仍需要进一步完善。
现阶段针对振动参数(振幅A0、振动频率f、振动时间t)研究仍为不同振动参数下动力响应问题。文献[11-13]分别采用有限元法和离散元法对振动压实过程进行模拟,量化出振幅、频率等振动参数对压实质量的影响,难以在模型中精确模拟机理。文献[14-15]基于试验方法,研究振动参数对压实质量的影响,但是以上研究主要是揭示单一振动参数对压实效果的影响,缺少压实过程中的振动参数的改进成果。伴随着无级调幅调频压路机出现,可以在压实过程中对压路机进行连续调频、调幅。德国BOMAG公司、瑞典Dynapac公司以及日本SAKAL公司等能根据填料的压实状态自动选择振动参数以达到较高的压实效率[16]。然而,上述的研究均通过调整振动参数,使得下一次压实度取得最大值,属于局部改进。而在压实过程中振动参数需要实时改进,使得填料更好、更快地达到最佳密实状态。同时,激振能量过大,容易导致振动压实设备出现“跳振”现象,这会减少振动压实设备的使用寿命,也会造成颗粒破碎增多,形成路基不均匀沉降病害[17-18]。因此,有必要在压实过程中实时改进振动压实参数,即基于填料的压实状态来实时调整压实参数,优化压实方法。
综上所述,目前缺乏压实过程中振动参数的动态优化方法,这限制了智能压实的发展,同时,振动参数过大容易引起压实设备损耗、颗粒破碎问题。为此,本文提出了一种基于能量最小原则的振动参数动态改进方法。首先,开展不同振动参数的振动压实试验,揭示振动参数与干密度的关系;其次,采用改进BP神经网络建立了干密度增量预测模型,根据能量最小原则采用遗传算法构建了压实过程振动参数优化方法;最后,基于Modbus 通讯,设计可振动参数可调的智能振动压实仪,并通过振动压实试验对改进结果进行验证和应用。
1 试验材料与方法
1.1 试验材料
试验材料取自于广湛高铁新兴段路基粗粒土填料,为花岗岩隧道矿渣,具有质地紧密、棱角较多等特点。填料的级配如图1所示。该填料级配最大粒径为45 mm,曲率系数为1.0,不均匀系数为80,最优含水率为6%。
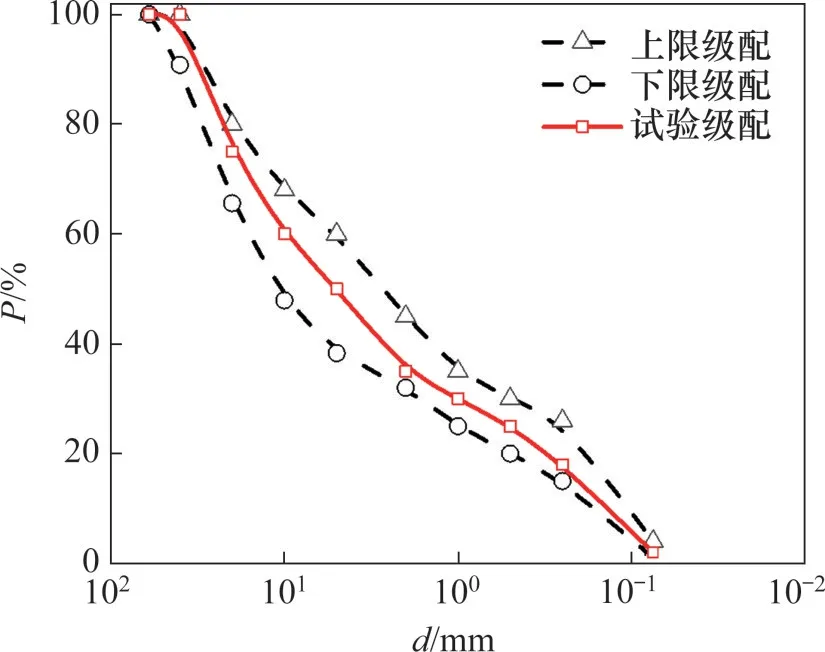
图1 试验材料的级配曲线Fig.1 Grain-size distribution curves of tested materials
1.2 试验仪器
试验采用自主研发的多参数可调式智能振动压实仪,如图2所示。设备振动单元空载单元质量为500 kg,配重块的质量M调节范围为0~480 kg,偏心距e0的调节范围为0~8 cm,偏心块m0质量范围为4.8~14.4 kg,振动频率f为0~40 Hz。在压实过程中,内置位移传感器可实时采集填料沉降,基于表面沉降理论[19],可自动输出干密度-时间曲线。

图2 智能压实设备示意图Fig.2 Diagram of intelligent compaction equipment
1.3 试验方法
振动压实试验主要包括以下3个步骤。
1)制样。将筛分得到的填料晒干,取质量分数为6%的水均匀喷洒于填料上,充分拌匀;将压实桶(内径为152 mm)内部涂润滑油,装入5 kg 填料拌匀;将压实桶置于振动压实仪下端固定位置处,使压缩板能恰好进入压实桶内。
2)振动压实。接通电源后,在图2所示的智能振动压实仪中预设f和t这2 个参数,并点击开始按钮。
3)数据采集。振动压实过程中采集试样干密度。压实桶与填料颗粒最大粒径比为3.8,满足规范[3]中对压实桶尺寸的要求。试验过程中模拟了多种工况,其中设t为4 min,振幅A0为0.15、0.30和0.60 mm,振动频率f为10、15、20、25和30 Hz。
2 粗粒土填料压实特性
2.1 振动参数
试样干密度随振动时间变化规律如图3(a)所示。从图3(a)可见:试样的干密度均随振动时间增加而呈现对数增长趋势。在不同振动频率下,试样获得最大干密度的振动时间是不同的。经对比发现,设置振动时间为4 min是合理的,即获得各组工况下的试样干密度稳定值。如无特殊说明,以下的干密度均代表振动4 min之后的干密度。
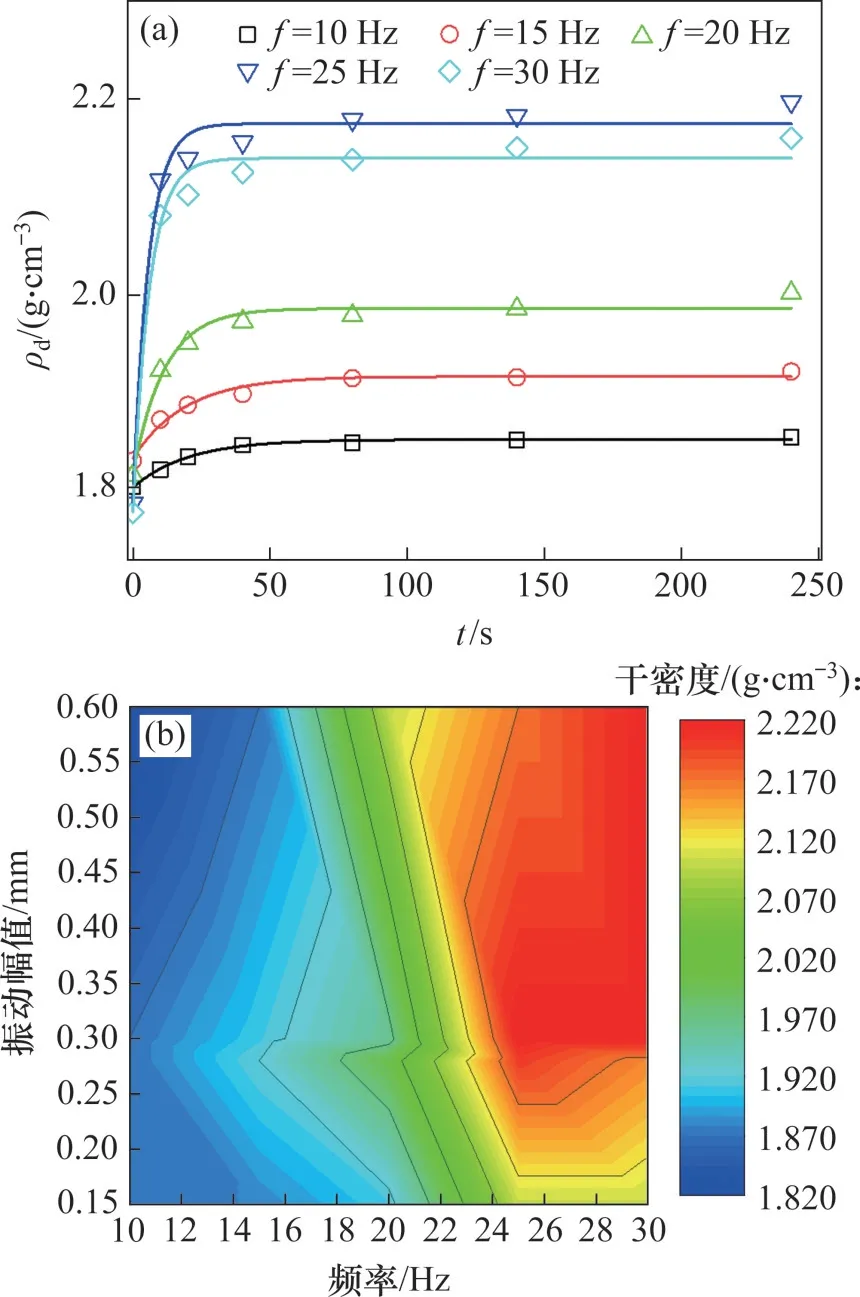
图3 不同工况试样干密度演化Fig.3 Evolution of dry density of specimens with different working conditions
从图3(a)可以发现:在不同振动频率下,填料的干密度不一样,这表明振动频率和振动幅值也会对填料干密度有重要的影响。图3(b)所示为振动频率和幅值与填料干密度的关系云图。无论振动参数为小频率、大振幅,还是大频率、小振幅,都很难获得较大的干密度,这主要是因为外界提供给填料压实条件使得填料颗粒只能在原位置附近进行小范围振动或者颗粒之间没有相对运动,无法有效填充填料颗粒结构中的大孔隙。只有在f≥25 Hz,A0≥0.3 mm时,试样能到达到最大干密度为2.22 g/cm3。当外界振动频率处于填料固有频率(25~30 Hz)时,填料颗粒处于共振状态,颗粒之间相对运动加剧,同时,振动幅值主要与填料高度相关,当外界振动幅值为0.3 mm 时,容器底部填料运动加剧,进而获得较大的干密度。
2.2 振动荷载和振动强度
在振动压实中,填料受到周期性的激振力作用,而使内部产生剪切应力,压实填料,激振力F计算式如下:
式中:Mp为振动系统质量;Ao为振幅;f为振动频率。
压实桶的直径×高度为15.2 cm×11.2 cm,填料上振动荷载Ps计算方法如下:
式中:S为激振头与压实桶的接触面积。
进一步,完整的振动压实工艺主要由设备静载、振动频率以及激振力所组成,三者的影响可以归纳为振动强度E的作用,计算方法如下:
式中:W为压实仪静载。振动荷载、强度与干密度的关系如图4所示。

图4 干密度与振动荷载、强度的关系Fig.4 Relationship between dry density and vibration load and strength
由图4(a)可知:干密度随着振动荷载增加而呈现出“缓慢增长—快速提高—平稳”3个阶段。
1)当振动荷载≤20 kPa时,试样干密度处于缓慢增长阶段,此时,试样所受动应力较小,颗粒之间相对运动较弱。
2)当振动荷载为20~110 kPa 时,试样干密度处于迅速提高阶段,颗粒之间振动响应增强,细颗粒可以迅速填充到粗颗粒孔隙中。
3)当振动荷载>110 kPa 时,干密度增长趋于稳定。而较大的振动荷载会加剧试样的破碎,造成试样级配变异,进而影响压实质量。振动荷载与试样干密度之间有一个包络区域,处于上包络线区域的振动荷载对应的共振频率为25~30 Hz,相反,下包络线区域的振动荷载对应的振动频率较低。即对于上包络线而言,较小的振动荷载可达到较大干密度。
同样地,振动强度与干密度之间也呈现出“缓慢增长—快速提高—平稳”3 个阶段。同时,振动强度存在阈值使得干密度达到最大值,后期的干密度趋于稳定。进一步增大振动强度会导致设备产生“跳振”现象,颗粒破碎加剧,严重影响设备寿命。
3 基于能量最小原则粗粒土压实质量动态优化方法
3.1 粗粒土压实质量动态优化算法
试样干密度并不是随着外部振动能量增加而增加。激振能量过大会导致振动压实设备出现“跳振”现象,也会造成试样颗粒破碎增多。随着试样压实度增加,试样的压实性能不断发生改变。理论上,每个压实状态均对应一个最优振动参数。因此,可以将试样的振动参数改进过程看作一个多阶段决策问题,每次振动参数的调整均对应一次决策。试样从松散状态到密实状态是一个完整的振动压实过程,对于每个阶段的振动参数选取需要考虑该阶段的决策对整个振动压实阶段的影响。
以填料压实度达到规范中要求的压实标准为基础,压实度计算如式(4)所示。为了保证整个振动压实过程中的能量输出最小,进而提高压实效率,将整个振动压实过程中的输出能量相加,输出总能量计算如式(5)所示。
式中:ρdi为第i状态下试样干密度;Δρdi为振动压实过程中试样的第i次相比于i-1 次的干密度增量;ρdi-1为第i-1 状态下试样干密度;A0i为第i状态下所选择的振动幅值;fi为第i状态下所选择的振动频率;K为压实度,高铁基床压实度取95%。
参数n通过干密度增量函数确定,每振动一次所增加的干密度与试样当前压实状态、振动频率和振动幅值有关,即满足式(6)。i=0,代表静压状态。当i>0时,第i状态下的试样干密度等于第i-1状态下试样干密度与第i状态下试样干密度增量之和,第i状态下试样干密度增量则通过第i-1状态下试样干密度与第i状态下试样所选择的A0i和fi来确定,计算公式如式(7)所示。
为了实现上述动态优化过程,首先,采用改进BP 神经网络建立了干密度增量预测数学模型;然后,基于GA 求解振动参数优化方法,其中GA的适应度函数是根据能量最小原则建立;最后,通过室内试验验证优化结果。优化算法流程图如图5所示。
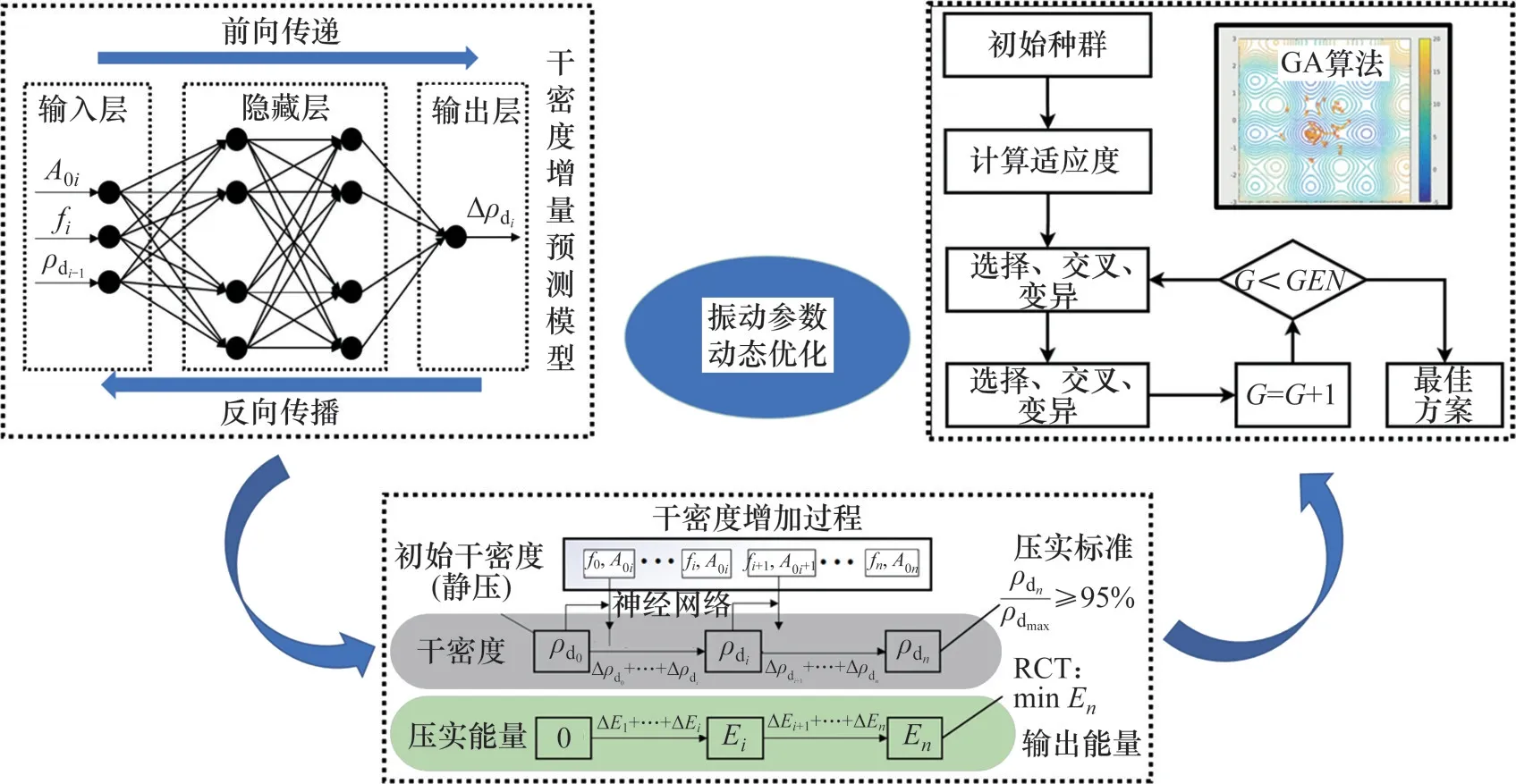
图5 基于能量最小的动态优化算法流程图Fig.5 Flow chart of dynamic optimization algorithm based on energy minimization
试样的干密度根据改进的BP 神经网络预测得到的干密度增量值累加得到,干密度增量预测模型构建主要包括3个部分即构建数据集、模型训练和模型测试,如图6所示。
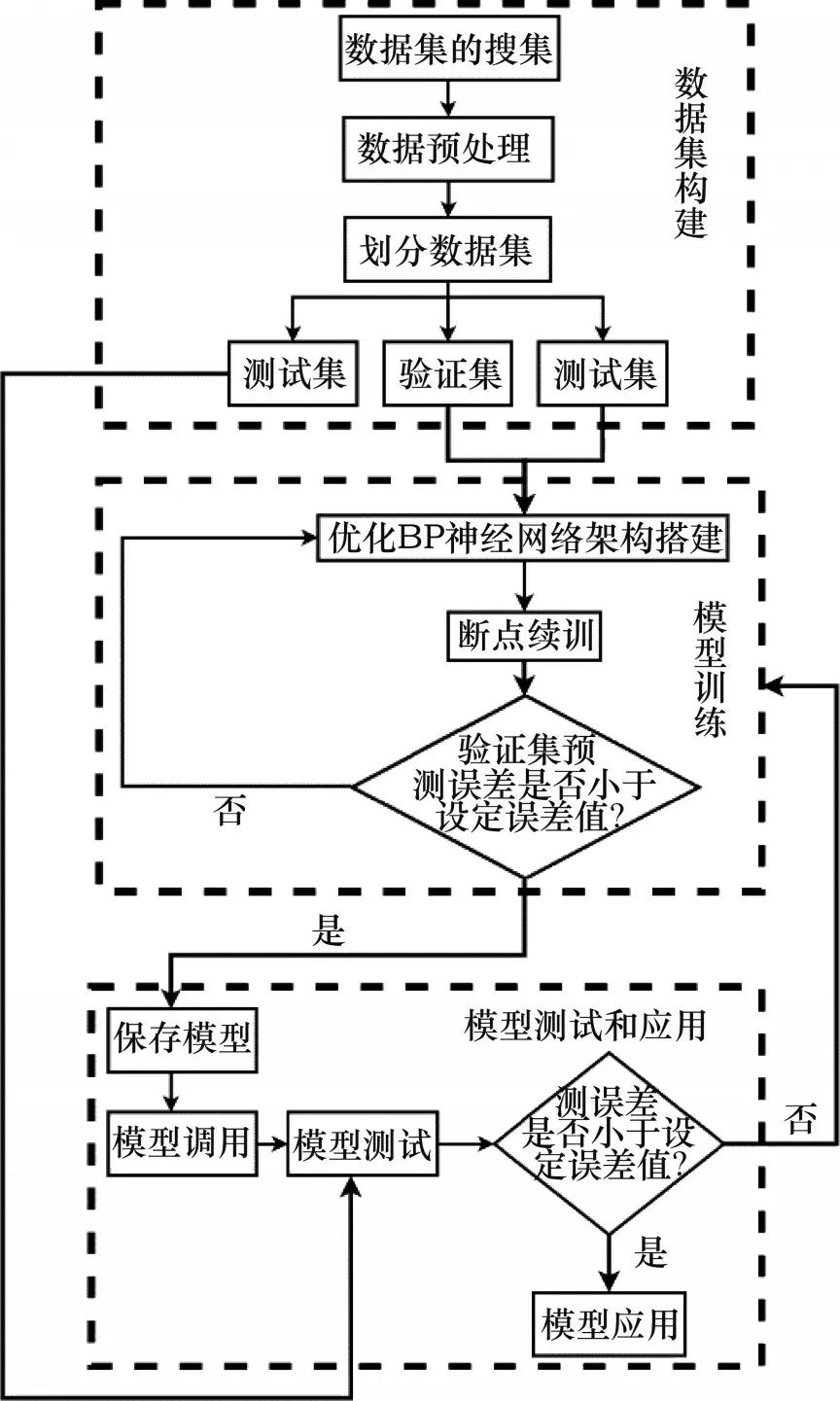
图6 改进BP干密度增量预测模型流程图Fig.6 Flow chart of improved BP dry density incremental prediction model
1)构建数据集。基于干密度-时间试验结果,建立试样振动压实过程振动次数与干密度间预测模型。基于试验发现,各个工况下干密度与振动次数关系符合双曲线模型。
式中:a和b分别为变量参数。
为消除不同变量的维度关系,需要对干密度进行归一化处理。
式中:y*为标准化后值;y、ymin和ymax分别为变量实际值、标准化区间的最大值和最小值。
将式(8)代入式(9),即得到干密度与振动次数预测模型:
式中:ρd为当前状态密度;ρmax为当前工况下压实稳定状态干密度,即最大干密度;ρ0为初始状态干密度;n为振动次数。
根据式(10)计算得到各工况下的模型参数,如表1所示,从表1可见:采用双曲线模型对压实过程干密度变化进行预测具有较高精度。
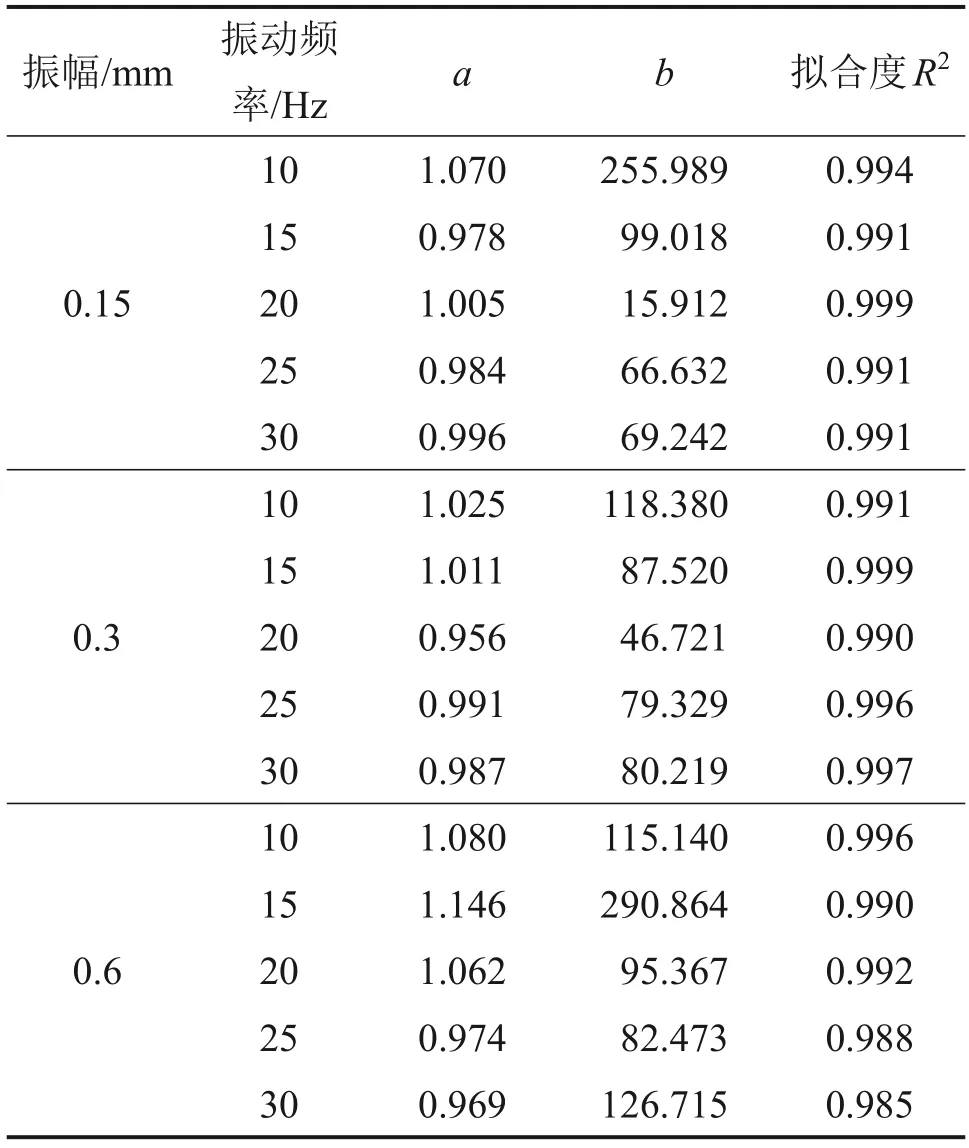
表1 模型参数及相关系数Table 1 Model parameters and correlation coefficients
以连续振动20 次为1 次完整振动,然后进行调频调幅操作,获得7 500组训练数据集。将数据集随机划分为训练集、验证集和测试集3 个部分,数据量占比分别为70%、15%和15%。
2)模型训练。在实际应用中,BP 神经网络算法也有几个不足之外,包括容易陷入局部最优、样本依赖性和学习率不可调等,从而使得干密度增量预测模型收敛速度慢甚至不收敛,最终影响干密度增量预测的精度。为了解决以上的问题,在传统BP神经网络的基础上引入改进学习率改进器AdamOptimizer算法,该方法根据损失函数的变化合理调整学习率,加速模型收敛速度[20-22]。
3)模型测试。干密度增量预测模型训练完成后被保存,测试时调用该模型,并将测试集输入。测试完成后,判断测试结果的误差是否小于设定误差,若满足则可应用该模型,反之重新执行步骤2)。
3.2 GA算法超参数优化
遗传算法的主要参数包括种群数量(PS)、选择概率(SP)、交叉概率(CP)和变异概率(Mu)[23-24],参数的取值影响着模型的精度和计算效率。取改进后的能量和遗传代数分别作为精度和计算效率判断的标准。为了保证计算速度和改进效果,在实际改进之前设置不同的初始参数并进行对比,最终确定遗传算法的合理参数。
在保持遗传代数为200 代,选择概率为0.90,交叉概率为0.70,变异概率为0.005不变的前提下,分别设置种群数量为50、100、150、200、250 和300个开展试验。不同种群数量适应度随遗传代数的变化曲线如图7(a)所示,由图7(a)可见,遗传到125 代时,这6 种适应度均逐渐收敛,收敛速度随种群数量增加而减小。为提高计算效率,最终确定种群数量为150个,遗传代数为200代。
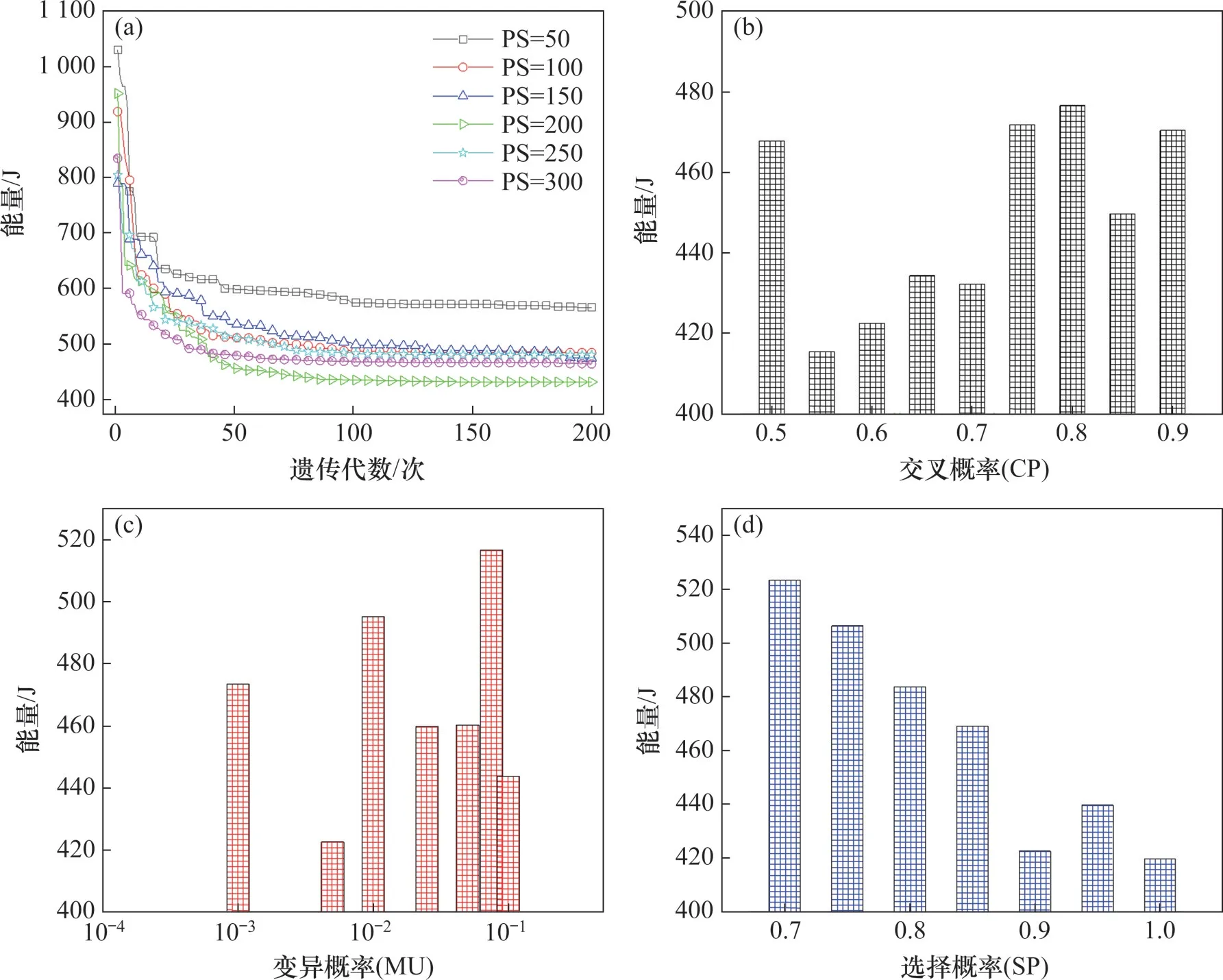
图7 GA算法参数选取Fig.7 GA algorithm parameter selection
遗传算法中建议的交叉概率为[0.50,1.00]之间。因此,设置交叉概率为0.50,0.55,0.60,0.65,0.70,0.75,0.80,0.85,0.90,在保证种群数量为150 个、选择概率为0.90、变异概率为0.005 不变的前提下,得到适应度变化如图7(b)所示,当交叉概率在[0.55,0.70]之间时,改进结果较为稳定,最终确定交叉概率为0.60。
遗传算法中建议的变异概率为[0.001,0.100]之间。设置变异概率为0.001、0.005、0.010、0.025、0.050、0.075、0.100,将种群数目设置为150,将选择概率设置为0.9,将变异概率设置为0.60,得到适应度与变异概率关系如图7(c)所示,变异概率过大容易使得适应度高的个体发生变异,导致改进结果收敛速度过慢,当变异概率位于[0.010,0.050]之间时,改进收敛速度快且改进结果较稳定,最终确定变异概率为0.025。
设置选择概率为0.70,0.75,0.80,0.85,0.90,0.95,1.00,种群数量为150,交叉概率和变异概率分别设置为0.60 和0.005,根据其计算的适应度来评估此组参数下改进结果的精度,适应度变化如图7(d)所示。从图7(d)可见:选择概率越大,改进后能量越小,为防止求解过程陷入局部最优解,最终确定选择概率为0.90。
通过分析遗传算法参数,最终设置种群数量(PS)为150,选择概率(SP)为0.9,交叉概率(CP)为0.6,变异概率(Mu)为0.05。
4 粗粒土压实质量动态优化算法应用
4.1 干密度增量模型预测结果
在训练集和测试集上,分别对传统的BP 神经网络和改进的BP神经网络进行模拟训练,得到模型在训练过程中的训练集损失值(简称loss)与验证集损失值(简称val_loss)变化规律如图8所示。
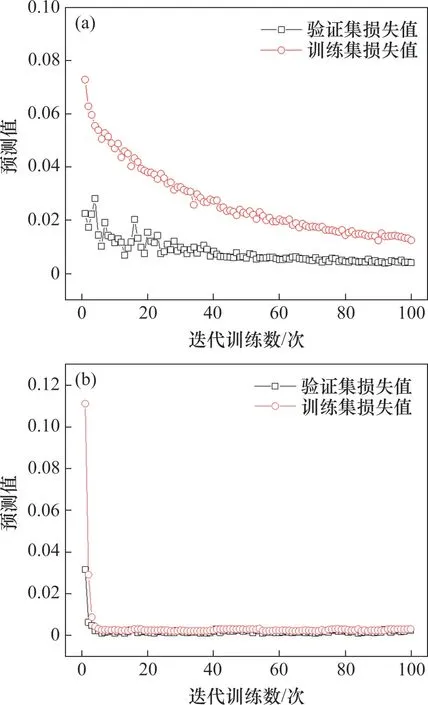
图8 两类模型的训练集和验证集损失函数曲线Fig.8 Loss function curves for training and validation sets of two types of models
从图8(a)可见:传统的BP 神经网络模型在训练过程中训练集损失值和验证集损失值下降速度慢且持续震荡,在100轮结束时,训练集损失值曲线仍未收敛,这主要是由于传统的BP神经网络使用SGD 算法,并没有引入动量法,并不能使梯度向量向相关方向加速变化,导致震荡现象。从图8(b)可见:改进的BP 神经网络模型在训练过程中训练损失和验证损失下降速度非常快;在第5轮迭代后,训练集损失值和验证集损失值便开始收敛,且未出现震荡现象,这是由于改进的BP神经网络引入了动量法,从而达到加速收敛的目的。同时,在整个迭代运算过程中,验证集损失值均小于训练集损失值,在迭代结束时,训练集损失值和验证集损失值都已经收敛完成,两者均接近于0,说明改进的BP神经网络模型训练效果较好,且在验证集上具有较强的泛化能力。
综上所述,改进的BP 神经网络模型具备可调节、收敛快的特点,解决了传统的BP神经网络模型收敛慢、容易陷入局部最优点的问题。
为了进一步测试模型的准确性,选择未参与训练的1 125组振动试验数据,同时采用已经训练好的传统BP 和改进BP 模型分别进行预测,并采用均方误差MSE和平均绝对误差MAE来评估预测结果。计算方法如式(11)和(12)所示,预测结果与实际值进行对比如图9所示。
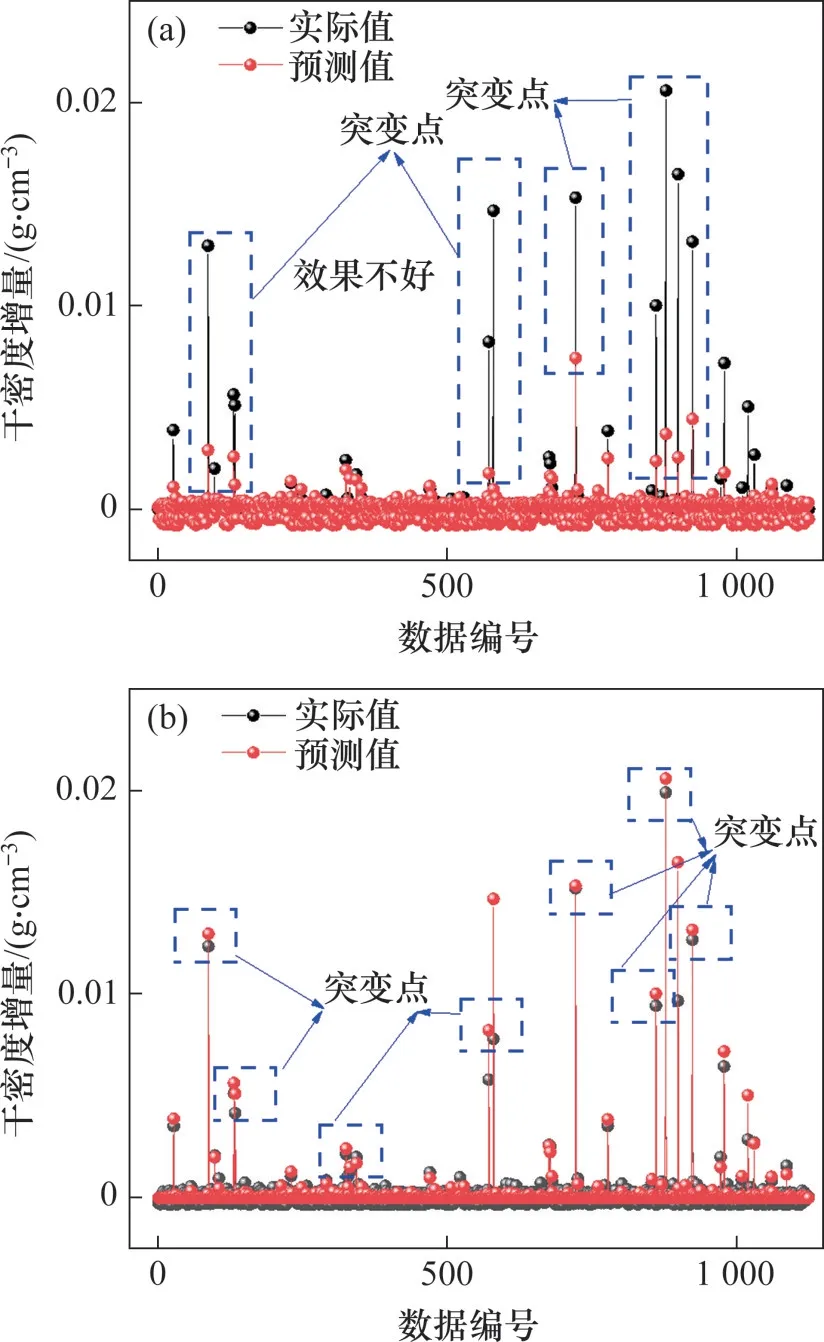
图9 两类模型干密度增量的实际值和预测值Fig.9 Actual values and predicted values of dry density increments for two types of models
式中:N为预测样本数量;yt和y′t分别为参数的实际值和预测值。
由图9 可知:传统BP 神经网络模型可以较好预测到绝大部分数据,但是对于某些干密度增量突出点预测效果不好;而改进的BP神经网络模型具有较强的预测能力,对干密度增量的起伏趋势都能很好地进行预测。改进的BP神经网络模型计算的MSE和MAE分别为4.5×10-6和1.4×10-3,而传统的BP 神经网络模型计算的MSE和MAE分别为6.35×10-4和5.1×10-3。因此,改进的BP神经网络模型不仅在训练集和测试集上表现优异,而且在测试集上的预测精度高,泛化能力强,能够很好地适用于干密度增量的预测。在后面的动态优化过程中,采用改进的BP神经网络进行干密度增量预测。
4.2 压实质量动态优化结果
振动压实过程的优化结果如图10所示。从图10(a)可见:优化后,振动频率随着振动压实过程由最初的10 Hz 逐渐增大到27 Hz,这一优化结果符合现有“最优频率会随着土体刚度增加而增加”的认识[25],证明了频率优化方案的可行性。同时,优化后,振动振幅随着振动压实过程先从0.15 mm开始逐渐增大,到连续振动120次时,振幅变化逐渐稳定,最终为0.34 mm。这是因为振动振幅为控制激振荷载及激振强度的重要因素,随着土体压密,需要更大的激振荷载来克服颗粒间的动摩擦力,使得颗粒发生相对位移[26-27],因此,选择逐步增大的振幅调整方案进行压实是可行的。从图10(b)可见:改进后的能量输出在整个压实过程中皆小于改进前的能量输出,并且最终有效减小了能量127.58 J,占改进前能量输出的25.61%。
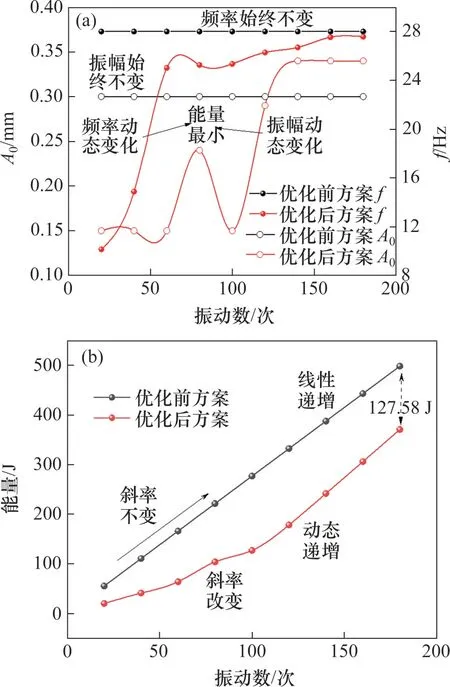
图10 优化前后试验方案下的振幅和能量演化Fig.10 Evolution of amplitude and energy under preoptimized and post-optimized tests schemes
综上可得,基于GA算法的动态优化方法能根据当前土体密实状态选择合适的振动参数,且在保证95%压实度的前提下能够有效减小振动过程中的能量,有效提升压实效率,减小对仪器的磨耗。
4.3 压实质量动态优化对比验证
为进一步确定优化后振动参数调整结果的准确性,采用改进后的方案进行室内振动压实试验。由于振动压实仪无法连续调幅,需要对振幅的输出方案进行调整,调整后的振动参数输出方案如表2所示。采用变频器对电机转速进行调节,采用Modbus 通讯协议开发振动压实仪配套智能控制软件,实时调节振动参数,实时监控仪器工作状态,结果如图11所示。
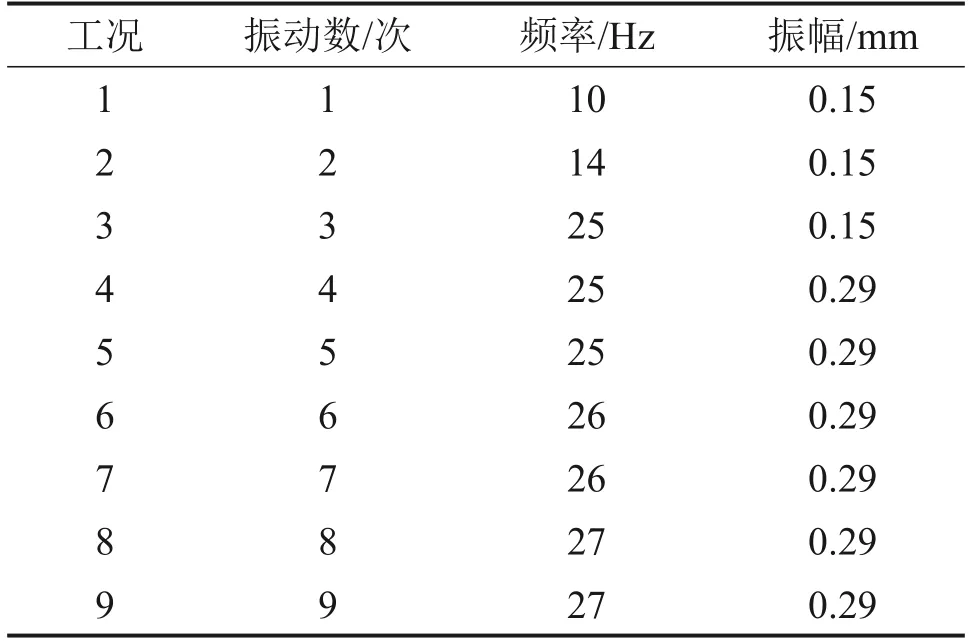
表2 优化后振动压实试验参数Table 2 Optimized parameters for vibratory compaction tests
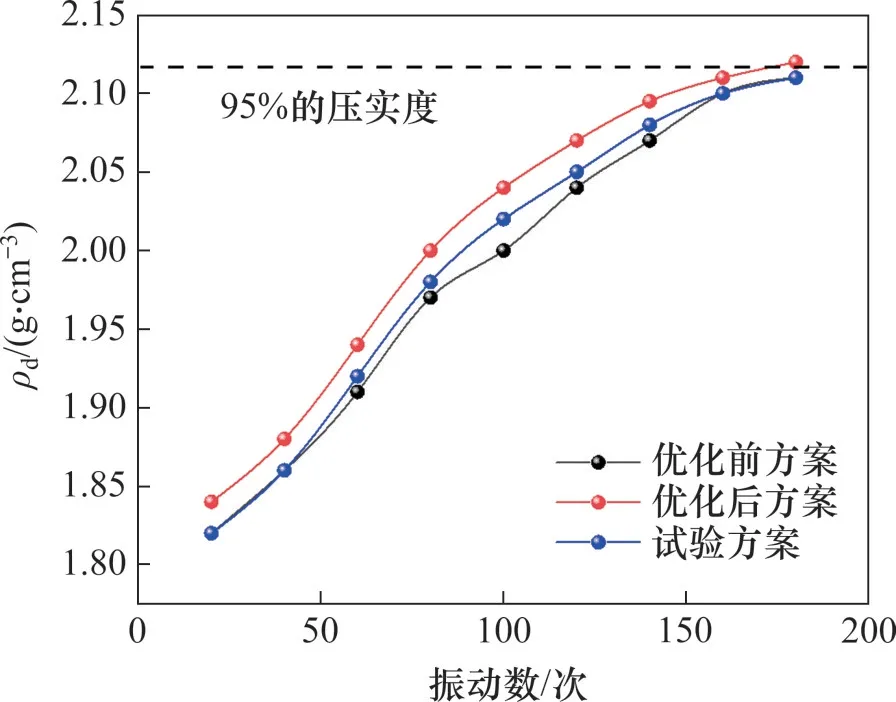
图11 优化前后试验方案下的干密度演化Fig.11 Evolution of dry density under pre--optimized and post-optimized test schemes
图11 展示了优化前后试验方案下,干密度与振动次数之间的关系。其中,优化后方案的干密度是根据建立的改进BP神经网络预测得到。从图11 可以看出:经过180 次连续振动(9 次完整振动)后,这3 种方案均能够达到压实度为95%的要求,且3种输出方案所需要的时间基本一致,整个过程需要12.5 s。统计压实前后土样级配,并计算相应的颗粒破碎率,发现采用改进调整后的试验方案进行压实的颗粒破碎率为3.2%,小于采用改进前的方案进行压实的颗粒破碎率(4.1%)。
因此,本文提出的基于改进BP 神经网络算法和GA的振动参数动态优化方法能够根据当前土体密实状态选择合适的振动参数,使得整个压实过程中压实器械输出的能量最小。
5 结论
1)振动强度存在阈值,使得干密度达到最大值,而进一步增大振动强度,会使得振动压实仪“跳振”。较大振动荷载会使得填料的破碎加剧,增加设备损耗,严重影响设备使用寿命。
2)引入AdamOptimizer 算法改进传统的BP 神经网络,建立干密度增量预测模型,有效提高了预测的收敛速度和精度,对于干密度增量突出点预测的适用性好。
3)提出适用于动态优化的GA 算法的模型参数。当种群数量为150,选择概率为0.9,交叉概率为0.6,变异概率为0.05 时,可有效保证动态优化方法的准确性。
4)经动态优化方法调整后,振动压实试验方案能减小振动能量127.58 J,较改进前的方案减少了25.16%,填料破碎率减小了0.9%,证明了方法的合理性。基于动态优化过程中振动频率和名义振幅的变化规律,建议在振动压实过程中可逐步增大其数值,以减小振动过程中的能量。
