基于PSO-BP神经网络的隧道内气动压力幅值预测
2023-10-30崔峰王汉封舒卓乐
崔峰,王汉封,2,舒卓乐
(1.中南大学 土木工程学院,湖南 长沙,410075;2.中南大学 高速铁路建造技术国家工程研究中心,湖南 长沙,410075)
高速列车在穿越隧道时,由于周围流场空间的突然变化,会产生压缩波和膨胀波。这2种压力波在隧道内以声速传播,导致隧道内的气动压力反复变化[1]。在这种气动压力的长期作用下,隧道衬砌和灯具、漏缆等附属设施可能会产生疲劳破坏的现象,使用性能和寿命都会受到严重影响[2-3]。因此,了解隧道内的气动压力变化特性,对保证铁路安全运营有着重要的意义。
目前,针对该问题的研究手段主要有:现场实测、动模型试验以及数值模拟等。刘峰等[4]通过实车测试研究了CRH 高速列车通过双线隧道时的瞬变压力及其变化规律。SAITO等[5]利用缩尺比为1/97的动模型试验平台,研究了变截面隧道内的压力变化规律。骆建军等[6]利用二维数值模拟方法对高速列车突入隧道时的压缩波进行了研究。但是,这些传统的方法存在着严重的不足。例如,现场实测只能针对既有隧道,且受环境因素影响较大,测试费用高,组织协调难度大;动模型试验前期准备工作繁杂、耗费时间长、费用高、数值模拟对计算资源要求高,周期长[7-8]。因此,寻找一种更为方便快捷的研究方法尤为重要。过去的研究已经积累了大量关于隧道内气动压力的数据,这为神经网络的在该问题上的运用奠定了基础。
神经网络具有强大的容错能力、自适应学习能力和优秀的非线性映射能力[9],在众多方面都有广泛的运用,如可靠性评估、图像识别、数据预测等。田明杰等[10]利用BP神经网络对隧道建设过程中的稳定性指标进行了较为精准的预测。FU等[11]通过模糊神经网络技术对大跨屋盖结构的风压进行了预测,实现了由部分测点的风压数据预测整个结构风压的目的。但是,关于神经网络在隧道内气动压力方面的应用目前尚无相应的研究。
基于以上分析,本文将BP 神经网络技术用于隧道内气动压力的预测,选取压力变化的幅值作为预测的指标。考虑到传统的BP神经网络存在容易陷入局部最优,导致训练效果不佳的问题[12],在模型建立的过程中引入PSO算法,建立PSO-BP神经网络模型,以实现对压力幅值精准预测的目的,为隧道内气动压力的研究提供参考。
1 数据收集与分析
1.1 隧道内气动压力幅值的影响因素分析
压力幅值ΔP(正负压极值之差,Pmax-Pmin)作为衡量隧道内气动压力变化程度的一个重要指标,受多个因素的影响。其中列车速度vtr、阻塞比α、列车长度Ltr、隧道长度Ltu和测点相对位置x等是最主要的5个影响因素。LIU等[13]研究了不同时速的列车通过隧道时的ΔP,发现ΔP与vtr的二次方呈正比。LI 等[14]通过改变隧道横截面积的方式研究了α对ΔP的影响,发现ΔP近似正比于α。NIU等[15]对不同编组列车通过隧道的情况进行了数值仿真分析,发现ΔP随Ltr增大而增大,当列车由3编组增加至16 编组时,ΔP的极大值也由3 578 Pa增长至5 267 Pa。周丹[16]研究了Ltu与ΔP之间的关系,发现两者的关系并不是单调的,ΔP会随Ltu增大先增大后减小的趋势,一辆8 编组的列车以350 km/h 的速度通过单线隧道,当Ltu取800 m 时,ΔP达到极大值6 985 Pa。沿隧道长度方向布置一系列测点,比较不同位置的ΔP,可以发现ΔP随x增大呈先增大后减小的趋势,ΔP的极大值一般出现在隧道长度的1/5~1/2处[13,15,17-19]。
ZHANG 等[20]对5 种不同形状的隧道入口进行了研究,发现隧道入口的形状对压力梯度有较大影响,对ΔP的影响很小。另外,本文的研究只针对流线型列车,根据CHEN 等[21]的研究,对于流线型列车,车头的长度对ΔP的影响很小,基本可以忽略不计,所以本文不考虑隧道入口形状和车头长度对ΔP的影响。
基于上述分析,本文选取的BP 神经网络输入变量为vtr、α、Ltr、Ltu和x,输出变量为ΔP。
1.2 数据收集与分析
可靠的数据是保证神经网络预测准确率的关键,本文从文献[14-18]中收集了575 组数据构成本次的数据集,其中部分数据如表1所示,收集的数据只考虑单车过隧道的情况。数据来源于现场实测、数值模拟和动模型试验3个方面,所占的比例分别为13.0%、70.9%和16.1%。
由于数据是从不同文献中收集而来,而且是通过不同的研究手段得到的,所以数据之间难免存在差异。例如,当8编组列车以300 km/h通过隧道时,不同的研究论文中距入口300 m 位置的ΔP如图1所示[19,22-24]。由图1 可知:数值模拟与现场实测值之间的最大差值为232 Pa,相对偏差为5.6%;数值模拟之间的最大差值为430 Pa,相对偏差达10.89%。也就是说,对于同一工况,不同研究方法所得结果会存在明显的差异;即使同样是数值模拟方法所得的结果也会存在较为显著的差异,这主要是因为网格尺寸、时间步长、湍流模型等的不同所带来的。

图1 不同文献中距入口300 m处的ΔP对比Fig.1 Comparison of ΔP at 300 m from entrance in different literatures
2 基于PSO-BP 神经网络的压力幅值预测模型
2.1 BP神经网络
BP 神经网络是一种基于误差反向传播训练的多层前馈神经网络,学习过程可以概括为:信号的正向传播、误差的反向传播、权值和阈值的更新。作为一种多层网络模型,BP 神经网络的结构一般由输入层、隐藏层和输出层构成,其中隐藏层可以是一层,也可以是多层。根据通用逼近定理[25],当隐藏层中具有足够多的神经元时,单隐藏层神经网络就可以以任意精度逼近任意函数。参考此定理,本文选择一个隐藏层,由此建立的BP神经网络结构如图2所示。
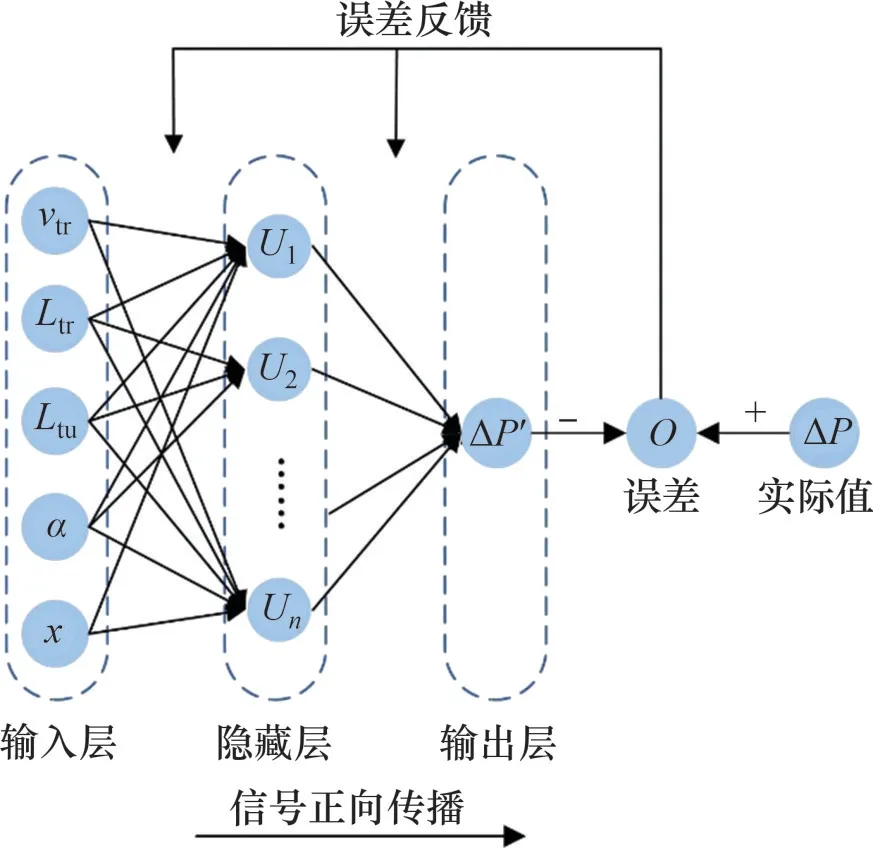
图2 BP神经网络结构示意图Fig.2 Structure diagram of BP neural network
2.2 PSO算法
PSO 算法是一种受自然启发的群体智能优化算法,源于对鸟群捕食的行为研究[26],其基本思想为:通过个体间的协作和信息共享来寻找最优解。在求解寻优问题时,会随机产生n个粒子,每个粒子都代表被优化问题的一个潜在最优解,携带位置信息X和速度信息v。粒子会通过自身的个体极值Pi和种群的全局极值G对速度和位置进行动态调整,过程为:
式中:ω为惯性权重;i=1,2,…,n;d=1,2,…,D;D为被优化参数的个数;t为当前的迭代次数;c1和c2为学习因子,取c1=c2=1.5;r1和r2为[0,1]之间的随机常数。为防止粒子的盲目搜索,将粒子位置限制在[-Xmax,Xmax],取Xmax=1.5;将粒子速度限制在[-vmax,vmax],取vmax=1.5。
为了更好地平衡PSO 算法的全局搜索和局部搜索能力,本文采用线性递减惯性权重[27]:
式中:ωstart为初始惯性权重,取ωstart=0.9;ωend为最大迭代次数对应的惯性权重,取ωend=0.4;tmax为最大迭代次数。
2.3 三阶段评估过程
为了减小预测结果的随机性,在整个过程中引入“三阶段评估过程”方法,即训练—验证—测试[28],过程如图3所示。首先,将整个数据集分为2部分:将90%的数据用于训练、评估模型,余下10%的数据作为模型的测试集;其次,利用交叉验证法选择模型的最佳参数,并通过交叉验证的结果比较2种模型的优劣;最后,建立一个基于整个训练集的模型,并使用测试集中的数据进一步测试模型的预测效果。

图3 “K折交叉验证法”和“三阶段评估过程”示意图Fig.3 Schematic diagram of "K-fold cross-validation method" and "three stage evaluation process"
交叉验证包括留一法交叉验证和K折交叉验证2种。本文中选择K折交叉验证方法,其大致思路为:将数据集等分为K个子集,每次选取K-1个子集训练模型,然后将余下的子集用于模型的验证,共进行K次交叉验证,最后返回K个测试结果的平均误差值作为模型的性能评估,这里取K=10。
2.4 PSO-BP神经网络模型
PSO-BP 神经网络的本质是通过PSO 算法对BP神经网络的初始权值和阈值进行优化,解决BP神经网络易产生局部极值的问题,从而提高预测精度。基于此原理建立的PSO-BP神经网络算法流程如图4所示。
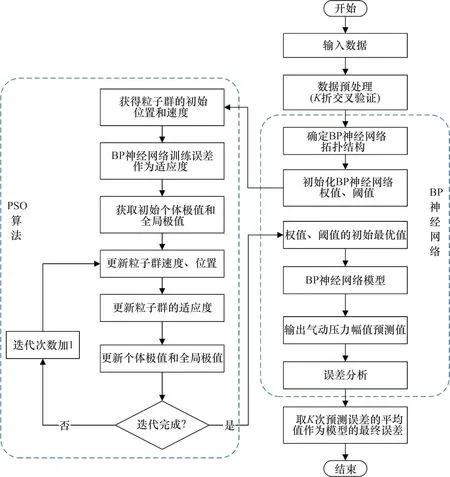
图4 PSO-BP神经网络流程Fig.4 Flow chart of PSO-BP neural network
在PSO-BP神经网络模型中,适应度函数的构造是一个关键的步骤。通过比较适应度,确定个体极值和全局极值,对粒子的位置和速度进行更新,从而完成PSO 算法的迭代寻优工作。本文以BP 神经网络的训练误差作为粒子的适应度,计算公式为
式中:S为训练样本的个数;Yj和Yj′分别为第j个训练样本中ΔP的实际值和预测值。
3 PSO-BP 神经网络模型参数的确定与优化
3.1 数据预处理
由于数据集内的数据属于不同的变量,其量纲不同、数量级差异巨大。若将这些原始数据直接输入BP神经网络中进行训练测试,则可能会出现梯度爆炸或者网络难以收敛的问题[29]。因此,数据输入模型前需要对其进行归一化处理,使之量纲一化并处于同一数量级。
本文采用的归一化方法为线性变换法,将数据通过最大-最小标准化映射到[0,1]之间,处理公式如下:
式中:y为归一化处理后的数据;x为原始数据;maxA和minA分别为某个变量对应的数据极大值和极小值。
3.2 确定BP神经网络结构
对于本文的神经网络结构而言,输入层和输出层中的神经元个数已经确定,关键在于如何确定隐藏层中神经元的个数。根据文献[9]的描述,隐藏层神经元个数可以通过下式进行确定:
式中:l为神经元的个数;m和n分别为输入变量和输出变量的个数;a为1~10之间的整数。在本文中,m=5,n=1,则l∈[3,13]。
为了进一步确定隐藏层中神经元的个数,以K折交叉验证的平均相对误差为评价指标,比较不同神经元个数对应的误差,结果如图5所示。由图5可知:当神经元个数为12时,训练集的平均相对误差最小。所以本文中BP神经网络的隐藏层神经元个数取为12,网络结构为5-12-1。BP神经网络的循环次数、学习率和学习目标分别设定为1 000、0.01和0.001。
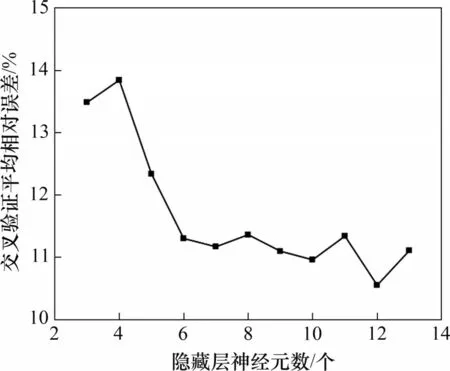
图5 不同神经元个数对应的平均相对误差Fig.5 Average relative errors corresponding to different numbers of neurons
3.3 PSO算法参数选取
对于PSO算法,种群规模(即粒子的数量)和迭代次数的取值起着至关重要的作用,种群规模和迭代次数太少,优化效果不理想;种群规模和迭代次数过多,又会导致计算时间过长。本文结合K折交叉验证,比较不同种群规模下适应度收敛时的平均迭代次数以及收敛后的平均适应度,以此选取较为合理的取值。
表2所示为不同种群规模迭代试验结果。由表2可知:随种群规模增大,适应度呈先减小后增大的趋势,当种群规模为100时,收敛后的适应度最小,说明此种群规模下的优化效果较好。随种群规模增大,计算完成所需的时间也在快速增加。另外,观察不同种群规模下适应度收敛时的迭代次数,发现所有的收敛迭代次数都在500 次以内。基于上述结果,本文设置种群规模为100,最大迭代次数为500。
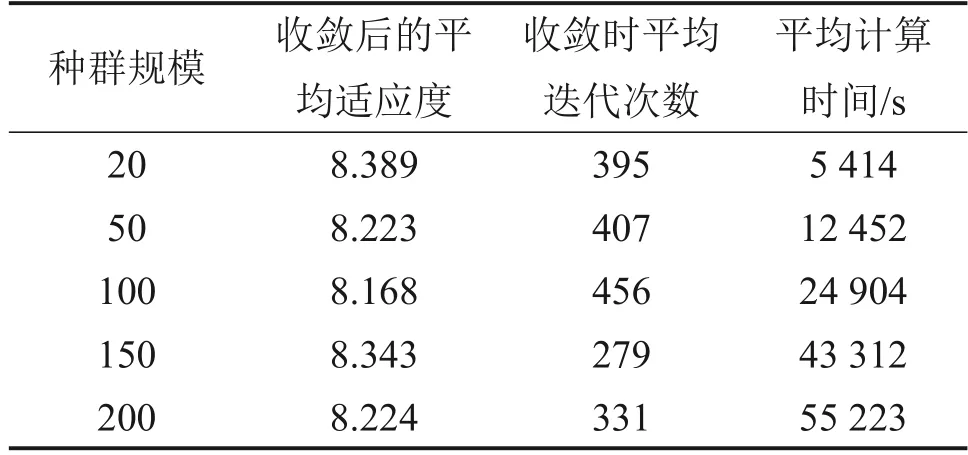
表2 不同种群规模迭代试验结果Table 2 Iterative test results of different population sizes
4 结果分析
4.1 PSO-BP压力幅值预测模型的验证
4.1.1 模型的评价指标
为了衡量模型的预测效果,采用决定系数(R2)、平均相对误差(EMAP)、平均绝对误差(EMA)和均方根误差(ERMS)作为评价指标,计算公式分别为:
式中:Yj和Yj′分别为第j个样本中ΔP的实际值和预测值;为样本中ΔP的平均值;N为样本个数。
4.1.2 交叉验证结果分析
表3所示为2 种模型的交叉验证结果对比结果,模型的各项评价指标均取K次预测结果的平均值。由表3可知:相比于BP神经网络,PSO-BP神经网络的预测值更接近实际值,决定系数由0.919增至0.961,平均相对误差(EMAP)、平均绝对误差(EMA)和均方根误差(ERMS)由11.08%、395 Pa 和551 Pa 分别降至7.26%、263 Pa 和381 Pa,分别降低了34.48%、33.42%和30.85%。以上结果表明,说明PSO算法在一定程度上解决了BP神经网络在训练过程中易陷入局部最优的问题,增强了BP神经网络的预测效果。

表3 交叉验证结果对比Table 3 Comparison of cross validation results
4.1.3 测试集预测结果分析
基于3.2 和3.3 求出的模型参数,利用全部的训练集数据训练模型,并使用测试集中的数据测试模型的预测效果。图6、图7 和表4所示分别为测试集的预测结果对比、2种模型的相对误差分布情况对比和2种模型的评价指标对比。

表4 2种模型的评价指标对比Table 4 Comparisons of evaluation indicators of two models

图6 测试集预测结果对比Fig.6 Comparisons of test set prediction results
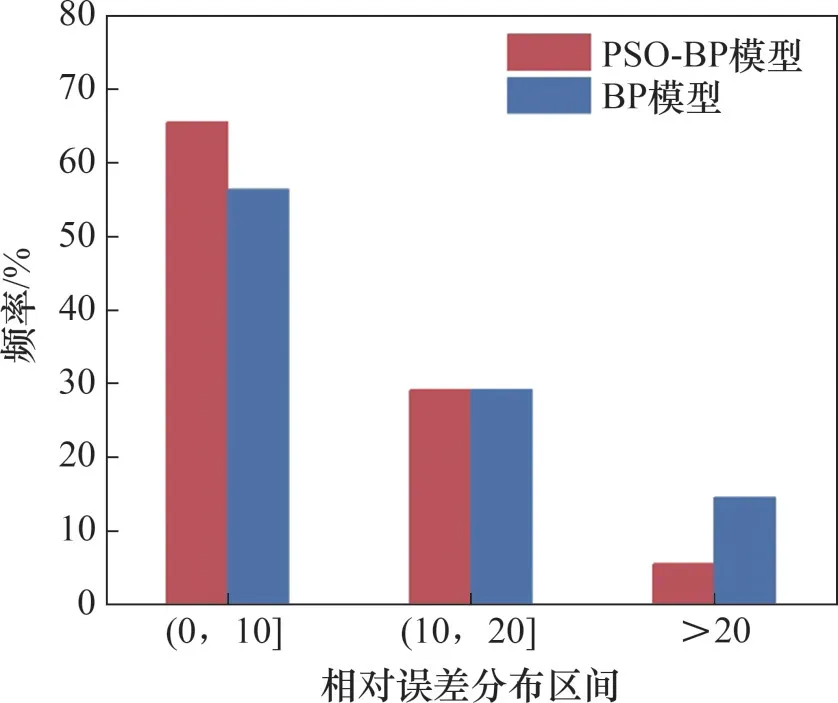
图7 2种模型的相对误差分布情况对比Fig.7 Comparisons of relative error distributions of two models
由图6 可知:对于测试集的预测,PSO-BP 神经网络的决定系数为0.953,比BP 神经网络的大,拟合优度更高,预测值和实际值更加吻合。由图7可知:PSO-BP神经网络中相对误差小于20%的比例高达94.55%,大于20%的比例只有5.45%;BP神经网络中相对误差小于20%的比例有85.46%,大于20%的比例有14.54%,说明PSO-BP神经网络的预测结果更加稳定,较少出现预测值和实际值之间偏差过大的情况。
由表4 可知:PSO-BP 神经网络的平均相对误差为7.84%,相比于BP 神经网络的13.06%,预测精度提高了39.97%。而且PSO-BP神经网络的平均绝对误差和均方根误差分别为295 Pa和390 Pa,较BP 神经网络的405 Pa、523 Pa,分别降低了27.16%和25.43%。结果表明PSO-BP 神经网络对于未知数据的预测效果比未优化的BP神经网络的效果好。
综上分析可知,PSO-BP 神经网络能够较为准确地预测隧道内的气动压力幅值,而且各项误差指标均比未优化的BP神经网络的指标小,具有更高的预测精度。
4.2 探讨压力幅值与各影响因素的关系
利用本文创建的PSO-BP 压力幅值预测模型,通过控制变量的方式,研究隧道内的气动压力幅值与各影响因素间的关系,相关规律如图8~12所示。

图8 ΔP与x的关系Fig.8 Relationship between ΔP and x

图10 ΔP与α的关系Fig.10 Relationship between ΔP and α
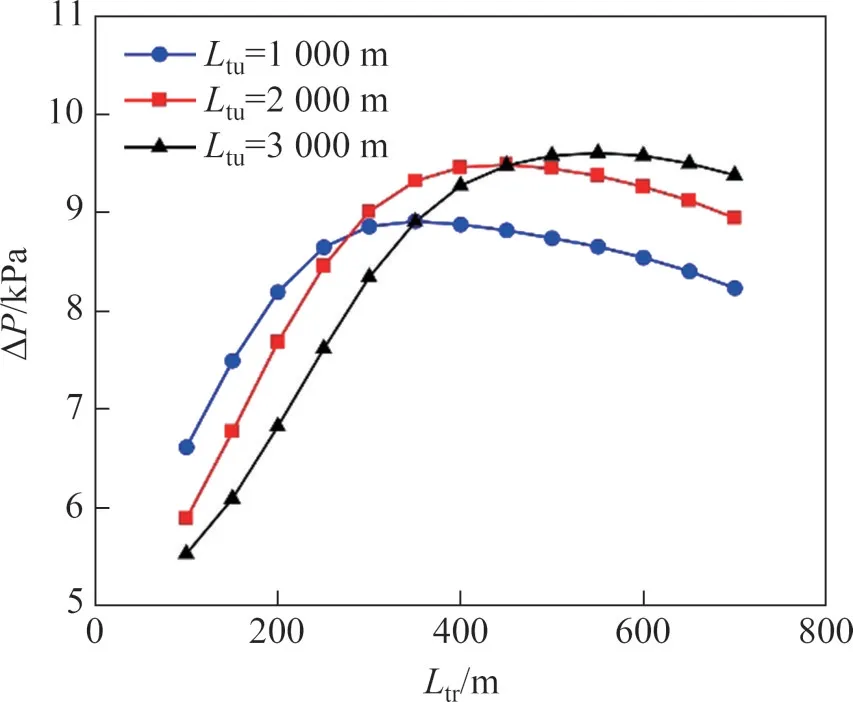
图11 ΔP与Ltr的关系Fig.11 Relationship between ΔP and Ltr

图12 ΔP与Ltu的关系Fig.12 Relationship between ΔP and Ltu
由图8~12可知:
1)ΔP随x增大呈先增大后减小的变化趋势,但极大值出现的位置并不固定。当车速为300 km/h时,极大值出现在隧道长度的0.4 处;当车速为400 km/h时,极大值出现在隧道长度的0.3~0.5处,说明ΔP极大值出现的位置与Ltr、Ltu以及vtr等多种因素有关。
2)ΔP与vtr的二次方呈正比,且与α呈正比。
3)ΔP随Ltr增大先快速增大后缓慢减小,存在一个最危险列车长度。最危险列车长度随隧道长度增加而增加,当隧道长度由1 000 m增至3 000 m时,最危险列车长度也由350 m增大至500 m。
4)ΔP随Ltu增加先增大后减小,同样存在一个最不利隧道长度。最不利隧道长度随列车长度增加而增加,当列车长度由200 m增大至400 m时,最不利隧道长度也由600 m增大至2 500 m。
通过上面的分析可以发现,通过PSO-BP神经网络模型得到的压力幅值变化规律与文献[13-19]的研究结果具有相似性,而且更为全面。这主要是由于PSO-BP神经网络模型能从数据样本中挖掘出规律,从而对未知条件下的压力幅值进行预测。
5 结论
1)对隧道内气动压力幅值的影响因素进行分析,提出了一种基于PSO-BP神经网络的压力幅值预测模型。
2)利用K折交叉验证法选择了模型的最佳参数,并证实了PSO对BP 神经网络的优化作用。
3)对于测试集的预测结果,PSO-BP神经网络的平均相对误差、平均绝对误差和均方根误差较未优化的BP神经网络分别降低了39.97%、27.16%和25.43%,具有更高的预测精度。
4)与相关文献中的研究结果相比,采用PSOBP 神经网络模型所得到的隧道内气动压力幅值变化规律更为全面。
