采用变分模态分解的微型燃气轮机发电系统混合储能功率分配策略

李月明,丁泽民,余又红,刘永葆

(海军工程大学动力工程学院,430033,武汉)

目前,电磁发射装置、轨道炮、大功率雷达和其他一些脉冲功率载荷在船舶上的应用日益广泛[1]。当脉冲负载连接到船舶电力系统运行时,短时间内消耗大量的电能[2]。与陆用大型电网不同,船舶电力系统是一个惯量小、容量小的孤立电网。由于作为原动机的微型燃气轮机的功率响应过程较慢,影响同步发电机的升压能力,电力系统无法提供并维持脉冲负载[3]的功率需求。因此,一旦接入脉冲功率负载,船舶电力系统短时间内很难保持稳定。储能系统被认为是缓解船舶电力系统功率波动的最有效的解决方案[4-6]。

飞轮储能系统(flywheel energy storage system, FESS)和超级电容器储能系统(supercapacitor energy storage system, SCES)具有低配置成本、高功率密度和良好的暂态调节性能等显著优势,是脉冲功率负载应用中最受欢迎的两种能量储能系统[7-8]。尤其是FESS,具有工作温度范围宽、瞬态响应及时、可靠性高、使用寿命长等特点[9],被广泛应用于新能源发电系统和船舶动力系统[10-15]。但是,FESS的能量密度相对较低,待机损耗较高[16]。蓄电池具有储能容量大、充放电功率小的特点。考虑到蓄电池与飞轮的互补特性,蓄电池通常与FESS一起组成混合储能系统(hybrid energy storage system, HESS)来提高电力系统的性能。此类HESS通常用作可再生能源系统的调频和负荷调节措施[17-18],也可以应用于船舶电力系统[19-20]。在船舶电力系统中,负载的功率变化比较明显,电源输出功率相对稳定。这与由采用光伏和风能发电组成的可再生能源系统的功率和负载特性有很大不同。船舶电力系统和可再生能源系统中HESS的总体控制策略也有较大差异。

关于应用FESS和蓄电池组成的HESS来缓解脉冲负载波动的研究,其对象集中在可再生能源领域的电力系统,而较少涉及船舶电力系统。对于船舶电力系统,HESS一般作为设备级储能,脉冲负载连接在其末端,此时HESS仅为脉冲功率负载[14]供电。这种架构虽然可以避免脉冲功率负载对船舶电力系统的影响,但并不能充分发挥船舶电力系统的性能,HESS也不能平滑其他负载的波动,如推进负载的变化[16,19-20]。一般情况下,脉冲负载比推进载荷对电网的冲击更大、要求的时间响应更快,所以本文主要研究脉冲负载的波动。

HESS补偿微电网功率波动的基本思想是将不平衡的功率按照频率高低进行分解[21],分解后的功率由各个储能系统通过控制变流器来响应,共同调节直流母线电压稳定[22]。常用的功率分配方法有滤波分解[23-24]、小波分解[25-26]、经验模态分解[27-28]和变分模态分解[29-30]等。但是,滤波分解中的低通滤波器在滤波过程中容易产生一定的延迟,这会导致储能系统功率的不合理分配。小波分解的结果对基函数的选择有很强的依赖性[29]。经验模态分解在递归分解过程中不能精确地将频率相同的模态函数分离,分解后的各模态函数存在模态混叠现象。变分模态分解(variational mode decomposition, VMD)可以自适应地确定各模态的最佳中心频率和带宽,并可以完成固有模态函数(intrinsic mode function,IMF)的有效分离和信号的频域划分。Dragomiretskiy等[31]于2014年提出了VMD算法,该算法通过多次迭代寻优,确定各分量的中心频率和带宽,最后获取分解分量,实现信号的准确分离,运算效率更高。VMD算法被广泛应用于变压器放电信号的提取[32]、风速监测[33]和可再生能源中混合储能系统的功率分配[29-30,34]等领域。变分模态分解的关键是设定合适的模态数K和二次惩罚因子α。文献 [29-30]分别通过粒子群算法和麻雀搜索算法优化VMD的参数,对风、光等可再生能源发电系统输出的波动功率进行分解,根据分解信号的频率特性,将各部分功率分别输送到不同的储能装置。仿真结果表明,参数优化的VMD算法优于滤波分解和经验模态分解(empirical mode decomposition, EMD)。文献 [34]提出了一种基于自适应VMD的HESS以平滑光伏功率波动,该算法可以自适应地确定分解模态个数和并网模态数,将HESS的功率分配给铅碳电池和超级电容器。为了验证该算法的优越性,建立了HESS的经济评价模型,结果表明,经过自适应VMD,不同天气情况下的光伏功率波动得到了明显的降低,与使用经验模态分解相比,在最大天气波动的条件下,HESS的生命周期年化成本也得到降低。

相比于可再生能源发电系统,燃气轮机作为发电原动机的船舶直流微电网电源的输出功率稳定,但是负载的突变会造成系统的功率供需不平衡,在利用HESS补偿船舶直流微电网系统功率不平衡时,同样面临HESS系统功率分配问题。在公开的文献中,VMD算法在船用燃气轮机直流微电网混合储能功率分配中应用还未见报道。本文根据VMD的算法特点,针对船用微型燃气轮机发电系统负载波动的问题,运用算术优化算法(arithmetic optimization algorithm, AOA)[35]优化VMD参数,提出一种基于算术优化算法优化的变分模态分解(AOA-VMD)算法,并在此基础上提出一种船用燃气轮机微电网混合储能功率分配策略。根据各储能装置的工作特性,实现HESS功率的初次划分。考虑到储能装置的安全稳定运行,设置飞轮、蓄电池模糊控制器,对初次分配功率进行修正,实现功率的二次分配。通过仿真验证了所提控制策略的有效性。

1 燃气轮机发电系统建模

本文建立船用微型燃气轮机发电系统整体模型,如图1所示。该系统由微型燃气轮机、带有励磁系统的三相同步发电机、二极管整流器、负载和混合储能系统组成。船用微型燃气轮机发电系统的电力由带励磁系统的同步发电机产生,可以满足系统的电力需求。同步发电机由一个100 kW的微型燃气轮机驱动,同时通过一个不受控的整流器(AC/DC)连接到直流母线。混合储能系统由蓄电池和飞轮储能系统组成;负载主要由日用负载、推进负载和脉冲负载组成,混合储能系统和负载经由变流器连接至直流母线。

1.1 微型燃气轮机建模

微型燃气轮机主要由压气机、燃烧室、涡轮机、转子4部分组成。本文根据各部件的气动热力学参数计算过程,对其进行模块化建模。

1.1.1 压气机

压气机的特征参数有折合流量Gcnp、压比πc、折合转速ncnp、效率ηc。已知其中两个参数,通过在通用特性图上插值的方法可得到另外两个参数值。选定压比πc和转速n作为输入量。压气机流量Gc、出口温度Tcout和耗功Nc计算式[36]如下

(1)

(2)

Nc=hcout-hcin

(3)

式中:Tcin为压气机进口温度,K;ka为空气的比热比;T1为压气机特性线测试进口温度,K;Pcin为压气机进口压力,Pa;P1为压气机特性线测试进口压力,Pa;hcout为压气机实际出口热焓值,kJ/kg;hcin为压气机实际进口热焓值,kJ/kg。

1.1.2 涡轮机

涡轮机的效率ηt、折合流量Gtnp、膨胀比πt、折合转速ntnp的计算方法与压气机的计算方法相似,都是通过在特性图上取插值的方法得到。涡轮机出口温度Ttout和输出功Nt计算式[37]如下

(4)

Nt=htin-htout

(5)

式中:Ttin为涡轮机进口温度,K;kb为燃气的比热比;ηt为涡轮机效率;htout为涡轮机实际出口热焓值,kJ/kg;htin为涡轮机实际进口热焓值,kJ/kg。

1.1.3 燃烧室

燃烧室进出口压力关系可以表示为

pbout=pbinσ

(6)

式中:pbin和pbout分别为燃烧室进出口压力,Pa;σ为燃烧室进出口压力损失系数。

燃烧室出口温度T3可由能量守恒方程[37]求得

(7)

式中:Ga和Gf分别为空气和燃料的流量,kg/h;Jf为燃料的热值,J/kg;ηb为燃烧效率;cp,a和cp,f分别为空气和燃料的比等压热容;T2a和T2f分别为燃烧室空气和燃料的进口温度,K。

1.1.4 转子

转子是将压气机和涡轮机以及负载连接起来的装置,涡轮机输出的功率用来带动压气机转动以及带动发电机运行,根据动量矩定律可以获得转子的数学模型[38]

(8)

式中:J为转子的转动惯量,kg·m2;n为转子转速,r/min;PG为发电机功率,W。

1.2 同步发电机建模

同步发电机在dq0坐标系下的电压、磁链和转矩方程[39-40]分别为

(9)

(10)

Te=ψdid-ψqiq

(11)

式中:ud、uq为机端电压d、q轴的分量,V;id、iq为负载电流d、q轴的分量,A;if为励磁电流,A;uf为励磁绕组电压,V;rf为励磁绕组电阻,Ω;iD、iQ为d、q轴阻尼绕组电流,A;uD、uQ为d、q轴阻尼绕组电压,uD=0,uQ=0;Xd、Xq为d、q轴同步电抗,Ω;Xad、Xaq为d、q轴电枢反应电抗,Ω;XD、XQ为d、q轴阻尼绕组电抗,Ω;ψd、ψq为d、q轴磁链,Wb;ψf为励磁绕组磁链,Wb;ψD、ψQ为d、q轴阻尼绕组磁链,Wb。

1.3 混合储能系统建模

HESS由蓄电池和FESS组成。将蓄电池的荷电状态SB和飞轮的当前转速ω定义为状态变量。控制变量为蓄电池的电流IB和飞轮转矩TF。HESS模型描述[17]如下

(12)

(13)

式中:QB为蓄电池最大容量,A·h;b和JF分别为飞轮的阻力系数和转动惯量。蓄电池和飞轮的输出功率如下

PB=IBVOC

(14)

PF=ωTF

(15)

式中:VOC为蓄电池开路电压,V。

1.4 脉冲负载建模

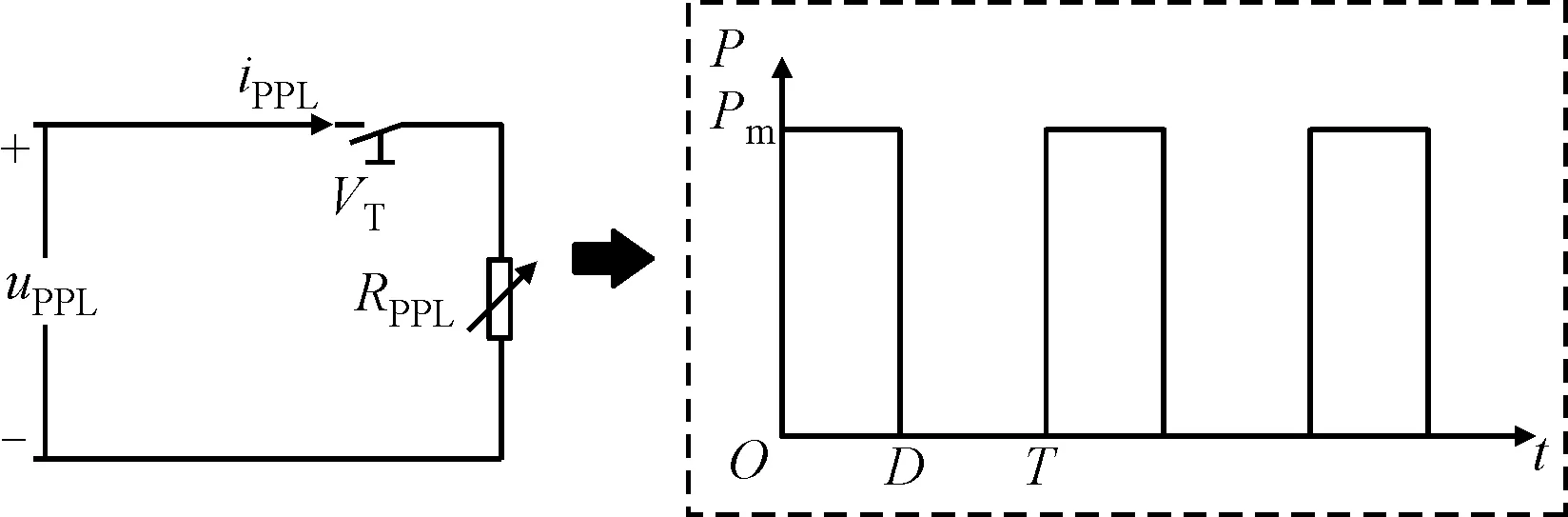
图2 单个脉冲负载等效结构Fig.2 Equivalent structure of a single pulse load

当脉冲负载接入时,其电阻很小,相当于短路状态。当脉冲负载不工作时,其电阻很高,相当于开路状态[41]。因此,脉冲负载可以用开关函数和可变电阻的形式来描述[42-43]。单个脉冲负载的等效结构如图2所示。图中:iPPL为流过脉冲负载的电流;RPPL为可变电阻,可用于设置脉冲负载的峰值功率Pm;D为开关管VT的占空比,代表脉冲功率在一个周期内的开启时间。

2 基于参数优化的变分模态分解原理

2.1 变分模态分解

为了发挥各储能元件的运行特性,通过VMD算法对微型燃气轮机发电系统脉冲负载功率波动信号进行分解。该算法是一种完全非递归信号处理方法,可以将时间序列数据分解为一系列具有特定带宽的IMF,每个IMF围绕确定的中心频率和带宽形成,并且带宽的总和值最小化[31,44]。在VMD算法中,每种模式带宽uk的导出过程[31]如下。

应用Hilbert对每种模式的功率波动时间序列数据进行分解,得到每个本征模态函数的解析信号,并得到其单边频谱A

A=[δ(t)+j/πt]*uk(t)

(16)

式中:*为卷积运算符;uk为VMD分解得到的第k个IMF分量。

通过加入指数算子e-jωkt,将每个本征模态函数的频谱调制到相应的基频带B,表示为

B=[(δ(t)+j/πt)*uk(t)]e-jωkt

(17)

式中:ωk为第k个IMF分量的中心频率。计算解调信号梯度的平均范数,估计出各本征模态函数的带宽。

带宽估计后,假定原始信号x(t)分解为K个IMF分量,保证分解序列为具有中心频率的有限带宽的模态分量。同时,各模态的估计带宽之和最小,约束条件为所有模态之和与原始信号相等,对应的约束变分问题为

(18)

式中:δ(t)为狄拉克分布函数。

为求取约束变分问题的最优解,引入二次惩罚因子α和拉格朗日乘法算子λ,将约束变分问题转变为无约束变分问题

L(uk,ωk,λ)=

(19)

采用乘法器的交替方向法来求解上述问题,在迭代计算中不断更新优化uk和ωk。对于所有ω′≥0,解表示为

(20)

(21)

重复上述步骤,直到满足迭代停止条件

(22)

2.2 算术优化算法优化VMD参数

由VMD算法原理可知,在对信号分解时需预设分解模态数K和二次惩罚因子α。K和α的选取不当会导致VMD分解后的信号与原始信号出现偏差。因此,选择合适的K和α是正确采用VMD算法分解功率波动信号的关键。在已有的研究中,粒子群算法和麻雀搜索算法被用于优化VMD的参数[29-30],但是其计算时长较长。Abualigah等[35]于2021年提出了AOA算法,是一种根据算术操作符的分布特性实现全局寻优的元启发式优化算法。该算法具有收敛速度快、精度高等特点。文献 [35]通过不同的场景对AOA的性能、收敛行为和计算复杂度进行了评估。实验结果表明,与包括粒子群算法和麻雀搜索算法在内的其他11种典型优化算法相比,该算法在解决具有挑战性的优化问题方面具有很好的效果。本文将AOA应用于VMD中,依据功率波动信号的特点自适应地调整VMD的参数K和α,避免了其选取不当而导致信号出现偏差的问题。

AOA优化算法分为3个阶段:初始化阶段、探索阶段和开发阶段。具体实现原理[35]如下。

(1)在初始化阶段,AOA随机生成一组候选解,每次迭代中的最佳候选解被视为获得的最佳解或迄今为止的近似最优解。

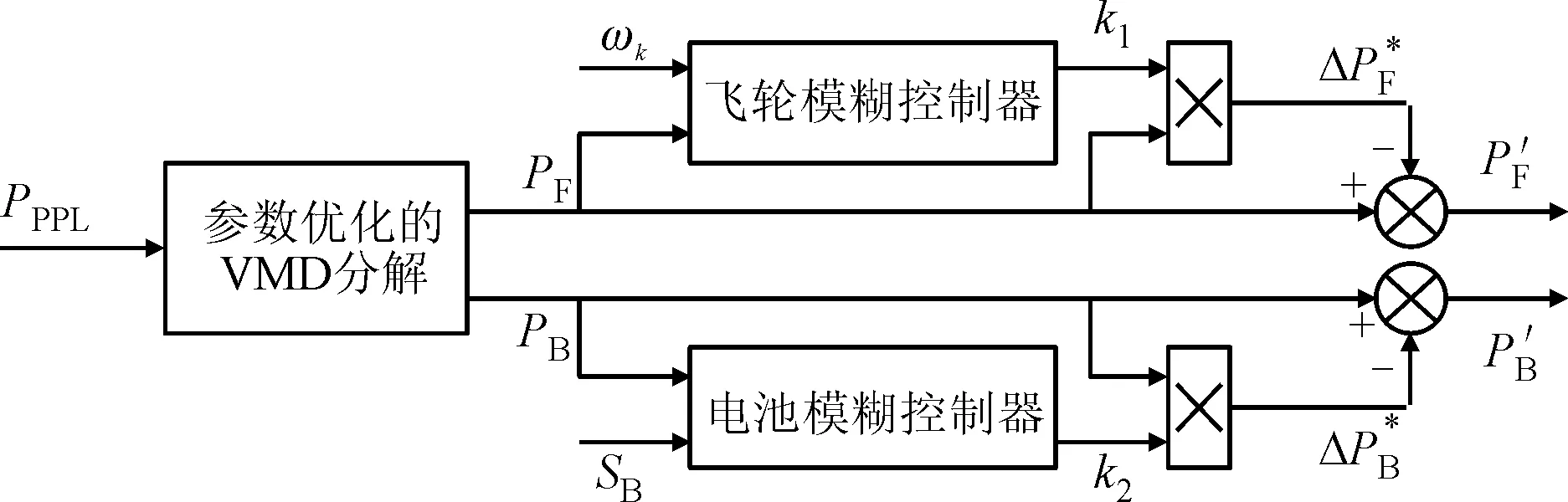
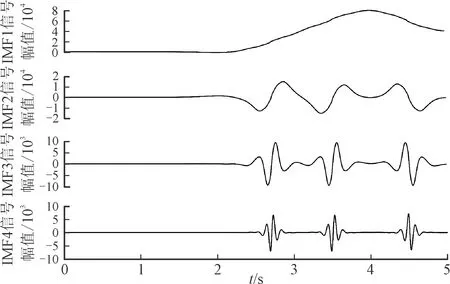
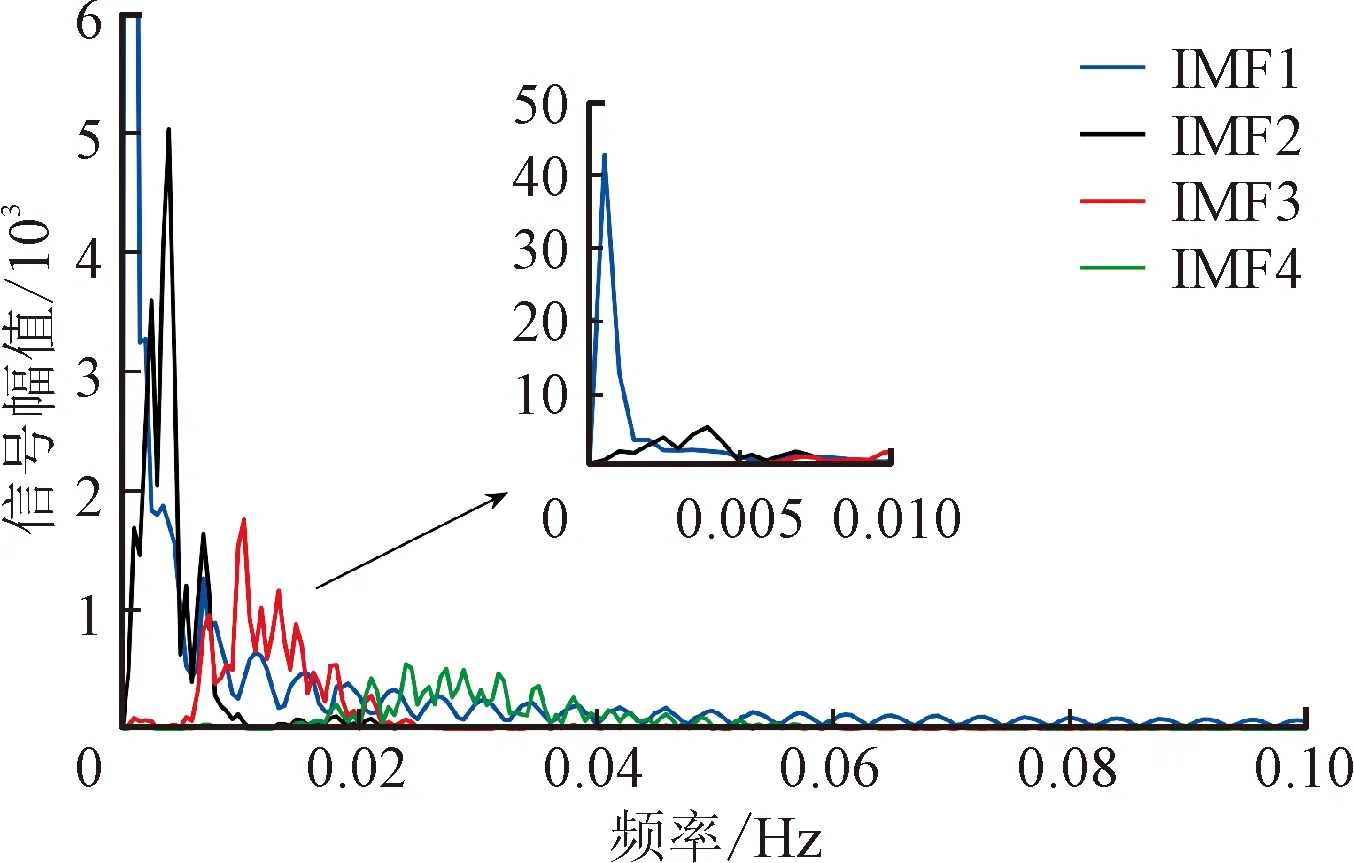
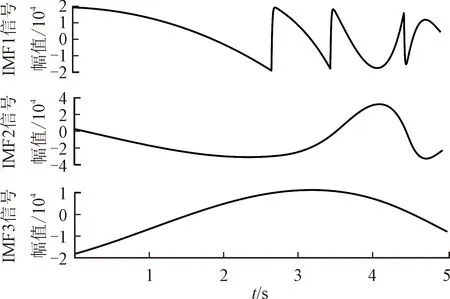
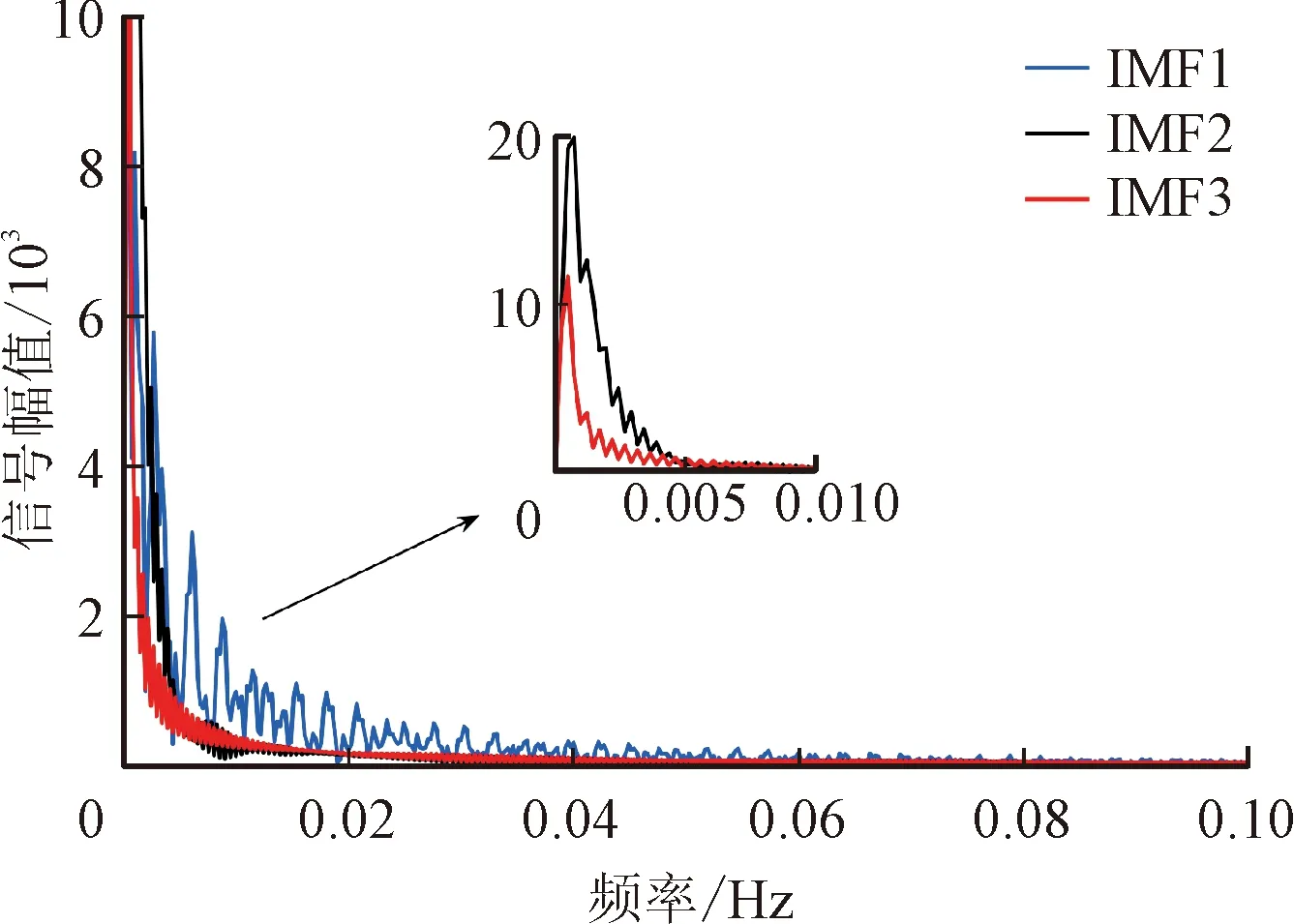
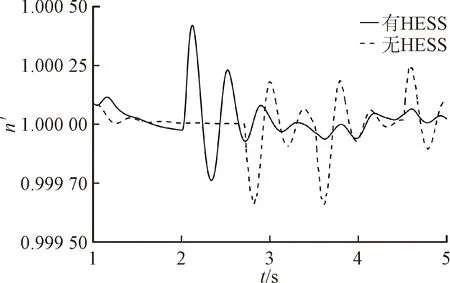
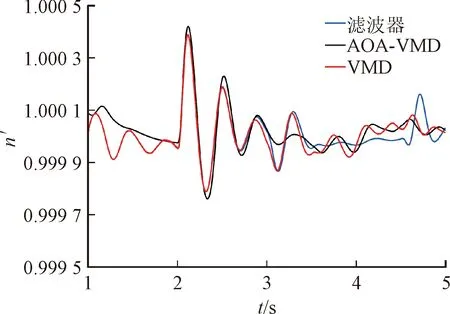
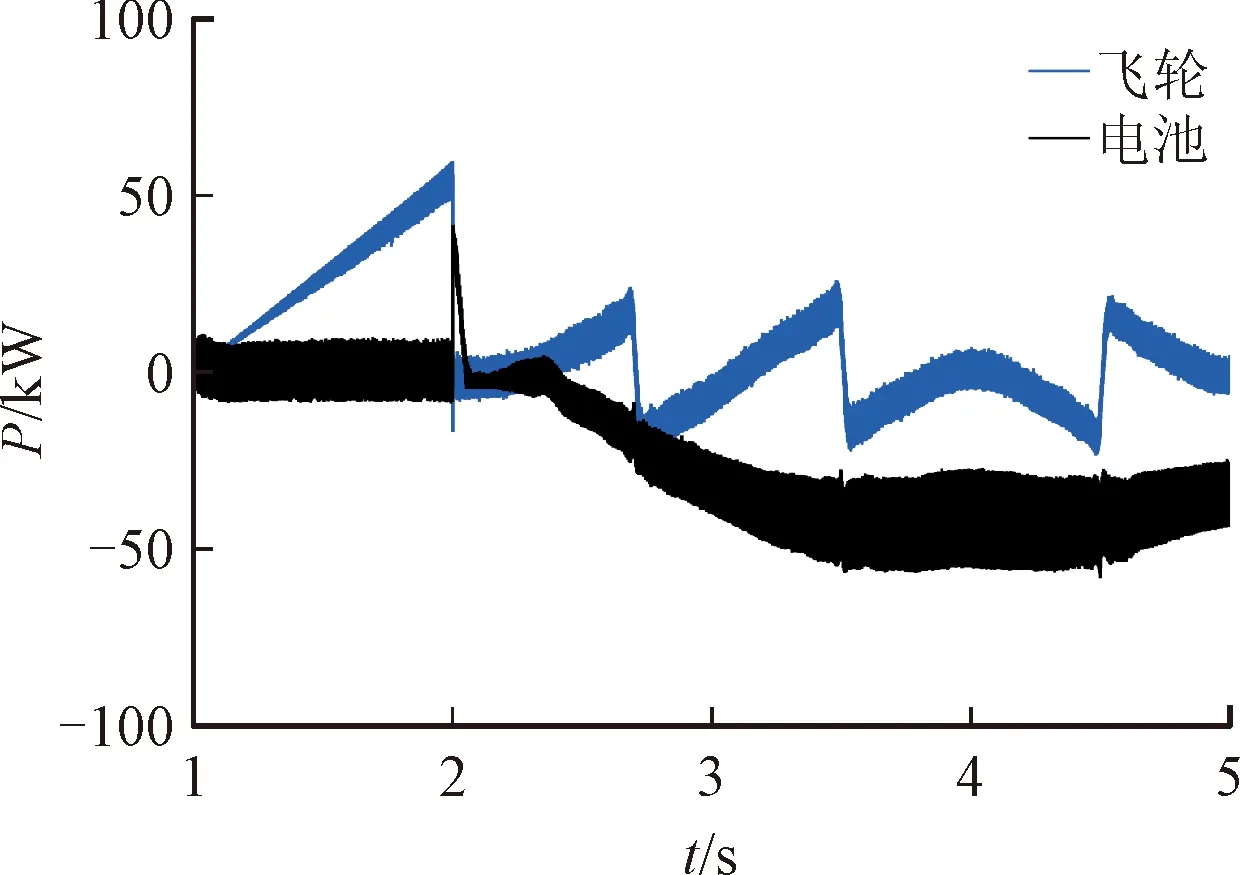
AOA通过数学优化器加速函数选择搜索阶段。r1代表0～1之间的随机数,F(t)代表第t次迭代时的加速函数值。当r1>F时,AOA 进行全局探索;当r1

F(t)=Min+t(Max-Min)/T

(23)

式中:Min与Max分别是加速函数的最小值和最大值,其值分别为 0.2 和 1;T是最大迭代数。

(2)在探索阶段,AOA通过乘法运算与除法运算实现全局搜索。r2代表0～1之间的随机数,H(t)代表第t次迭代时的数学优化器概率。当r2<0.5时,执行除法搜索策略;当r2≥0.5时,执行乘法搜索策略。位置更新公式如下

X(t+1)=

(24)

式中:μ是调整探索过程的控制参数,设为0.499;ε为一个极小值;LA和LB分别表示给定搜索空间的上边界和下边界。数学优化器概率计算公式如下

(25)

式中:α′是敏感参数,定义了迭代过程中的局部开发精度,α′越大,则迭代次数对H(t)的影响越大,此处取值为5。

(3)在开发阶段,AOA利用加法运算与减法运算实现局部开发,位置更新公式如下

X(t+1)=

(26)

式中:r3代表0～1之间的随机数。

3 微型燃气轮机发电系统混合储能功率分配策略

燃气轮机的燃烧机理导致输出机械功率变化缓慢,这种缓慢的响应特性不能满足脉冲负载功率快速变化的要求。为了保证船用微型燃气轮机发电系统持续稳定提供电能,减少脉冲负载对微型燃气轮机的影响。本文利用HESS主动提供微燃机发电系统脉冲负载的功率需求,在稳态运行的模式下,燃气轮机为系统提供能量。当脉冲负载接入时,优先由HESS提供能连,只有当HESS提供的功率无法满足需求时,微燃机才额外为脉冲负载提供能量。脉冲负载的功率由HESS补偿,通过设置HESS的分配策略,将HESS所需补偿的功率进行合理的分配。混合储能系统需要补偿的功率为

PHESS=PPPL

(27)

式中:PPPL为脉冲负载的功率。

3.1 混合储能功率的初级分配

本文将脉冲负载的功率作为VMD算法的输入量,经AOA-VMD算法自适应地将脉冲负载的功率分解为一系列频率由低到高的IMF,然后对各IMF进行Hilbert变换,观察各IMF在边际频谱域上的信号特征,利用各模态混叠现象严重程度来确定高低频分量界限。考虑到混合储能系统中各储能元件的特性,将低频分量分配给蓄电池、高频分量分配给飞轮储能系统。各储能装置功率的计算公式如下

(28)

式中:N为高、低频分量的界限;PB(t)和PF(t)分别为对应的蓄电池和飞轮的初始功率参考值。

3.2 混合储能系统功率的二次分配

运用VMD算法实现了HESS功率的初级分配,但初级分配没有考虑电池的荷电状态和飞轮的转速,在投入过程中如果造成过充过放,不仅会严重影响储能装置的性能和寿命,也会影响下一次脉冲负载接入时系统能量的补偿。在混合储能功率分配过程中,模糊控制器具有改善储能系统的充放电功率的特点[45-46]。因此,本文设计了两个模糊控制器,如图3所示。

图3 本文设计的两个模糊控制结构Fig.3 Fuzzy control structure

设置相应的模糊控制规则,对蓄电池和飞轮储能系统充放电功率进行修正,实现HESS功率的二次分配,修正后的充放电功率为

(29)

飞轮储能模糊控制器的输入为PF(t)和ω,输出为修正系数k1,输入输出选用梯形和三角形隶属度函数,ω的论域为 [0, 1],模糊子集为{VS, S, M, B, VB},表示{很低,低,中,高,很高}。PF(t)的论域为 [-1, 1],模糊子集为{D, C},表示飞轮放电或充电。k1的论域为 [-1, 1],模糊子集为{NB, NS, ZO, PS, PB},表示{负大,负小,零,正小,正大}。对应的飞轮储能模糊控制器规则如表1所示。

表1 飞轮储能模糊控制规则

蓄电池模糊控制器的输入为功率PB(t)和荷电状态SB,输出为修正系数k2,输入输出选用梯形和三角形隶属度函数,SB的论域为 [0, 1],模糊子集为{VS, S, M, B, VB},表示{很低,低,中,高,很高}。PB(t)的论域为 [-1, 1],模糊子集为{D, C},表示蓄电池放电或充电。k2的论域为 [-1, 1],模糊子集为{NB, NS, ZO, PS, PB},表示{负大,负小,零,正小,正大}。对应的蓄电池模糊控制器规则如表2所示。

表2 蓄电池模糊控制规则

4 仿真案例

为验证所提控制策略的有效性,对如图1所示的船舶微型燃气轮机直流电力系统进行仿真分析。直流母线电压参考值为513 V。蓄电池的类型为锂电池,标称电压为400 V,额定容量为100 A·h,初始荷电状态为50%。FESS的最大充放电功率为60 kW,最大转速为1 200 rad/s。蓄电池和飞轮的上、下限边界分别为SB,min=30%、SB,max=90%、ωmin=30%和ωmax=80%。脉冲负载的峰值功率为40 kW,周期为3 s,占空比为60%。初始状态下,电网中连接10 kW日用负载,2.7 s时接入一个脉冲负载,3 s时加入10 kW的日用负载,3.5 s时接入另一个脉冲负载,这两个脉冲负载的功率都为40 kW。考虑HESS时,在1 s时给飞轮储能系统充电,2 s时飞轮储能系统充电结束,达到额定转速。

考虑HESS时,脉冲负载的功率需求由HESS主动提供,微型燃气轮机作为备用功率源,在HESS无法提供足够的功率时,微型燃气轮机提供不足的功率。同时,微型燃气轮机也承担日用负载的功率需求。对于利用HESS来满足脉冲负载的功率需求:首先,采用参数优化的VMD算法对脉冲负载的功率进行分解,得到各储能装置的初次分配功率;然后,经由各储能装置的模糊控制器,对初次分配功率进行修正,得到各储能装置的二次分配功率,即各储能装置需要提供的功率。采用AOA算法迭代计算可得VMD中最优参数组合 [K,α]= [4, 3 140]。

为了进一步验证本文所提参数优化VMD算法的优势,分别采用VMD和EMD算法对脉冲负载的功率PPPL进行分解,将对分解后的结果进行Hilbert变换,并对比分解后的IMF频谱特性。图4(a)为脉冲负载功率经参数优化VMD算法分解得到的结果,对其进行Hilbert变换,得到的各IMF频谱如图4(b)所示。

观察图4(b)可以看出,IMF1和IMF2间模态混叠现象较为轻微,IMF2～IMF4混叠较明显。因此,选择IMF1分解信号作为蓄电池需要平抑的初级功率,选择IMF2～IMF4分解信号作为FESS需要平抑的初级功率。然后,经模糊控制器对初级功率进行修正,得到电池和FESS各自需承担的功率,实现对HESS功率的合理分配。

(a)分解结果

(b)各IMF频谱

图5(a)为脉冲负载功率经EMD算法分解的结果,图5(b)为分解结果经Hilbert变换后得到的各IMF频谱。从图5(a)中可以看出,PPPL经EMD分解为3个IMF,这3个IMF在整个仿真期间都有所波动。从图4(a)可以看出,PPPL经VMD分解为4个IMF,这4个IMF只有在脉冲负载功率波动时才会产生相应的信号,相比于EMD分解,参数优化的VMD分解更加精确。从图5(b)可以看出,经EMD分解后不同频率成分混叠严重,高低频分量不易区分。从图4(b)中可以看出,经VMD分解后不同IMF的频率较易区分,分布较为规律。因此,相对于EMD,参数优化的VMD能更准确地通过区分高低频量的方式完成对HESS功率的合理分配。

(a)分解结果

(b)各IMF频谱

在接入或不接入HESS的情况下,脉冲负载造成的直流母线电压(Udc)波动和微燃机转速(n′,标幺值)波动分别如图6(a)和6(b)所示。从图6(a)可以看出,不接入HESS时,在2.7 s和3.5 s分别连接峰值功率为40 kW的脉冲功率负载,Udc瞬间由513 V跌落至478 V,跌落幅度为6.8%,给系统带来较大扰动。接入HESS时,脉冲负载的功率需求主要由HESS补偿,因此其对直流母线电压的影响很小。在FESS充电结束,即2 s时,直流母线电压由510 V上升至534 V,上升了4.7%,该扰动小于接入40 kW脉冲负载所带来的扰动。从图6(b)可以看出,不接入HESS时,2.7 s连接脉冲负载,微燃机的转速变化率为0.036%。接入HESS时,2 s飞轮储能系统充电完成,微燃机转速变化率为0.04%。《GB/T 13030—2009 船舶电力推进系统技术条件》对船舶电网供电系统要求,转速波动率应控制在±0.5%[47]。因此,两种情况下同步发电机的转速都在稳定运行的范围内。由图6可以看出,不接入HESS,脉冲负载对系统产生周期性的冲击,影响直流母线电压和微燃机转速的稳定运行。接入HESS,脉冲负载产生的冲击由HESS平抑,转速变化率最大为0.02%,母线电压波动量最大为3 V。由此可以看出,接入HESS后,脉冲负载几乎不会对直流母线电压和微燃机转速产生影响。这进一步体现了本文设计的储能装置控制策略的有效性。

(a)Udc变化特性

(b)n′变化特性

为了验证采用本文AOA-VMD算法对船用燃气轮机直流微电网混合储能中飞轮储能和蓄电池功率分配的控制效果,分别运用滤波器、VMD和AOA-VMD对脉冲负载的功率进行分解,得到FESS和蓄电池的初级分配功率,然后经相同的并联模糊控制器调节,得到FESS和蓄电池的二次分配功率。3种混合储能功率分配策略下,直流母线电压Udc和微燃机转速变化率n′的波动如图7所示。

(a)Udc变化特性

(b)n′变化特性

由图7可以看出,在3.5 s接入一个峰值功率为40 kW的脉冲功率负载,采用AOA-VMD算法分解脉冲功率负载所造成的Udc和n′波动最小,其中母线电压Udc由513 V跌落至511 V,跌落幅度为0.4%,转速变化率n′跌幅为0.008%。4.5 s时突卸峰值功率为40 kW的脉冲功率负载,同样地采用AOA-VMD算法所造成的Udc和n′波动最小,采用未优化的VMD算法的波动次之,而采用传统的滤波器方法分解脉冲功率负载所造成的波动最大,ΔUdc和Δn′具体的变化情况如表3所示。对比采用滤波器和未经优化VMD的算法,采用AOA-VMD算法分解脉冲负载的功率波动信号,投入峰值功率为40 kW的脉冲功率负载时,直流母线电压波动量ΔUdc分别减小3 V和2.4 V,对应的微燃机转速波动率Δn′分别减小0.012%和0.014%。切除上述负载时,ΔUdc分别减小2.7 V和0.6 V,Δn′分别减小0.018%和0.012%。由以上分析可知,针对船用燃气轮机直流微电网混合储能中飞轮储能和蓄电池的功率分配,AOA-VMD的控制效果优于滤波器方法和未经优化的VMD算法。经参数优化的变分模态分解算法的应用有效地提高了系统的稳定性。

图8给出了发电机、负载、电池和飞轮功率变化特性。由图8(a)可以看出,与负载投切时的快速功率变化相比,发电机的功率变化相对缓慢,不能及时响应脉冲负载功率需求。

表3 不同功率分配策略下Udc和n′的波动特性

(a)发电机和负载的功率变化特性

(b)电池和飞轮的功率变化特性

从图8(a)可以看出,在2.7 s接入脉冲负载时,微型燃气轮机的输出功率基本不变。此时,脉冲负载的功率需求由FESS和电池共同提供,如图8(b)所示。从图8(b)可以看出,飞轮在2.7 s放电之前会预充一部分能量,预充电时间约为0.2 s,保证飞轮转速不会跌落过低,飞轮预充电所需的功率由电池提供,避免飞轮充电对直流母线电压和微型燃气轮机的稳定运行造成影响。在3 s接入10 kW的日用负载时,微型燃气轮机动作提供这部分功率需求,如图8(a)所示。飞轮在3.5 s接入脉冲负载之前会预充一部分能量,这部分能量由蓄电池提供,预充电时间大约0.2 s,最大充电功率为20 kW。在3.5 s接入另一个峰值功率为40 kW的脉冲负载时,FESS由充电状态瞬间转变为放电状态,为系统提供20 kW的瞬态功率,此时蓄电池向系统提供的总功率为45 kW,燃气轮机提供的功率为35 kW。

在3.5～4.5 s之间,两个脉冲功率负载处于叠加状态,而HESS可提供的功率有限,无法满足两个脉冲负载叠加所需的功率。因此,脉冲负载需求的功率与HESS提供的功率的差值由微型燃气轮机提供。在4 s时燃气轮机输出功率达到最大,为51 kW,如图8(a)所示。此时功率波动恢复平稳,但功率需求较大。由于FESS被用来补偿瞬态功率波动,因此在4 s时FESS处于待机状态,无功率输出。蓄电池用于补偿系统长时间的功率需求,因此在4 s时蓄电池处于最大功率放电状态,功率输出为49 kW,如图8(b)所示。在4.5 s突卸脉冲功率负载之前,飞轮储能会释放一部分能量,释放的能量提供给脉冲负载,减少了微型燃气轮机和蓄电池的功率输出,同时可以避免飞轮转速在突卸脉冲负载后上升过大。在4.5 s突卸其中一个峰值功率为40 kW的脉冲负载时,飞轮瞬间由放电状态转变为充电状态,最大充电功率为20 kW,此时蓄电池和微型燃气轮机向系统提供的功率分别为44 kW和36 kW。

在4.5～5 s之间,FESS逐渐恢复到待机状态。此时,微型燃气轮机与蓄电池提供给系统的功率逐渐减小,直至减小到维持一个脉冲负载的功率需求。由以上分析可知,采用本文所提出的能量分配和储能协调控制策略,微型燃气轮机与HESS具有良好的配合能力,保证了在多样化负载脉冲负载条件下发电燃机、电网、混合储能装置之间的协同运行。

5 结 论

本文将参数优化的VMD算法应用到考虑蓄电池和飞轮组成的混合储能系统的船舶微燃机直流微电网中。在不接入HESS时,微型燃气轮机提供系统的能量需求。接入HESS时,脉冲负载的功率需求主要由HESS提供,微型燃气轮机的功率需求与HESS提供的功率的差值由微型燃气轮机提供。运用经算术优化算法优化的VMD算法实现对混合储能功率的初级分配。同时,为了保证储能装置运行在安全稳定的范围内,实时监测飞轮转速和蓄电池的荷电状态,采用两个并联的模糊控制器,实现了储能装置的二次功率分配。对所提出的控制策略进行了仿真分析,结果表明。

(1)HESS的应用可有效改善系统对大功率脉冲负载的响应能力。接入船舶微型燃气轮机发电系统时,HESS主动提供脉冲负载所需的功率,当HESS无法提供足够功率时,由微型燃气轮机提供剩余的功率需求。考虑混合储能后,脉冲负载投切所造成的直流母线电压最大波动减小6.4%,对应的微燃机转速最大变化率减小0.02%。

(2)经参数优化的变分模态分解算法的应用有效地提高了系统的稳定性。对比采用传统滤波器和未经优化VMD的算法,采用AOA-VMD算法分解脉冲负载的功率波动信号,投入峰值功率为40 kW的脉冲功率负载时,直流母线电压波动量分别减小3 V和2.4 V,对应的微燃机转速波动率分别减小0.012%和0.014%。切除上述负载时,电压分别减小2.7 V和0.6 V,转速波动率分别减小0.018%和0.012%。