基于延时等概率符号化传递熵分析的脑肌耦合双向神经信息传递规律研究

张凯,徐光华,2,李文平,江开元,田沛源,郑小伟,韩丞丞,张四聪

(1. 西安交通大学机械工程学院,710049,西安; 2. 西安交通大学机械制造系统工程国家重点实验室,710054,西安)

随着我国老龄化程度的持续加深,脑卒中疾病和意外脑损伤引发运动功能障碍的患者数量大幅增加[1],而手作为人体的精细感知和运动交互器官,在大脑皮层中面积占比大、功能复杂,因此手部运动功能极易受到损伤且难以修复[2]。神经接口作为一种融合生命科学与工程技术的前沿技术,能够通过有效提取患者神经信号中包含的运动意图。利用信号处理将其数字化为外部设备的控制指令,以辅助患者实现对外部设备的控制,从而实现主动运动意念参与的康复训练,促进其手部运动功能恢复,因而得到了广泛的研究和应用[3-5]。其中,脑电信号(EEG) 能够从中枢层面反映患者残存神经的运动意图[6],而肌电信号(EMG) 能够体现肌肉的活动状态,体现了四周神经对于运动任务决策的神经响应[7]。同步耦合EEG与EMG不仅能够更加全面地反映大脑对于肢体运动控制神经环路的工作机制,以有效指导神经接口界面的设计,从而帮助有一定自主性运动能力的患者进行手部精细动作的康复训练[8]。同时,可以利用两种信号的同步耦合关系来分析运动控制通路的功能状态,为脑卒中患者的运动机能进行客观量化的评价[9]。

然而,现有的研究只关注脑肌电信号模式识别的问题,忽略了对脑肌耦合的内在作用规律和双向传递机制的研究,从而导致现有脑肌耦合神经接口存在着可解释性差,控制准确率低等问题。脑肌电耦合通常指的是大脑皮层的运动控制信息会引起相关肌肉组织的同步振荡活动[10-11],且该种振荡存在双向性,研究脑肌电耦合分析方法,不仅能够有效揭示运动控制环路的神经信息内在作用机制,且能为高鲁棒性的多层次脑肌耦合神经接口模型提供理论支撑[12]。现有应用于脑肌电信号的耦合分析方法从原理上可以分为线性方法和非线性方法[13-14]。其中,以相干性分析、格兰杰因果分析为主的线性分析方法虽然具有计算简便、可靠性高的优点,但不能满足对脑肌电信号耦合的非线性特征的提取与辨识[15-17]。以互信息为主的非线性方法虽然可以对脑肌电的非线性过程进行刻画,但是不能衡量系统状态变化所带来的动态信息变化。传递熵[18]通过计算转移概率衡量系统间的动态信息传递,能够分析时间序列间的非线性信息传递关系,是衡量两个时间序列信息定向传递的指标,为脑肌电信号的耦合分析提供重要研究手段[19-20],然而,传递熵计算前需通过相空间提取和还原信号的动态特性,因此要求信号的长度足够长,且传递熵的计算复杂度却较高,极大限制了其应用。

基于此背景,本文面向脑肌耦合双向神经信息传递规律开展研究,结合脑肌电信息传递的特征,将时间序列符号化的方法与传递熵计算相结合,提出了延时等概率符号化传递熵方法,以实现在粗粒化信号序列降低计算复杂度的同时保留脑肌电信号的动态特性,避免符号化过程中未考虑信号中出现幅值较大的突变噪声会造成区间划分不恰当,导致少数符号代替大部分原始观测值的问题,以防损失大量原始时间序列中的信息。同时,基于所提方法开展在线实验验证,以揭示从脑肌电层面上的大脑皮层和运动肌肉间的双向信息传递内在作用机制,为强鲁棒性神经接口设计提供有力的理论支撑。

1 脑肌融合的神经传导功能延时等概率符号化传递熵分析

传递熵通过衡量系统之间的信息交换来获得系统的结构化信息,能够获得系统中的动态信息和信息交换的方向性,该方法能够衡量两个时间序列间的双向非线性耦合特征,是研究脑电与肌电间信息交互的理想方法。为了避免传递熵相空间提取和还原过程的计算复杂度,研究人员将时间序列符号化的方法与传递熵计算相结合[21],一种典型的变尺度符号化的方法如下

R=

(1)

式中:R为符号化后的序列;x(i)为原始信号序列;k为符号化的数量;δ为递增常量,其取值为(max(x)-min(x))/k。

基于该思路,研究人员提出变尺度符号化传递熵方法对脑肌电信号进行同步分析[22],其数学表达式为

(2)

式中:xn+τ为时间延迟τ时的信号X符号化观测值;xn为信号X的符号化观测值;yn为信号Y的符号化观测值。

符号化传递熵能够保留系统的动态特性并简化传递熵的计算,由于其在符号化过程中未考虑信号中出现幅值较大的突变噪声会造成区间划分不恰当、导致少数符号代替大部分原始观测值的问题[23],损失了大量原始时间序列中的信息。同时,脑肌电信号间的耦合关系并不仅是简单直接的信息传递,由于大脑皮层到手部肌肉之间通过神经通路连接,而神经元信息传递存在延迟,可以推断大脑与肌肉间的控制信息传递和感知反馈间必然也存在一定延迟[24-25]。传统的传递熵分析方法仅考虑两个时间序列间信息定向传递的方向,并未考虑两个时间序列之间存在时间延迟的情况,所以直接使用传统的传递熵方法对同步采集的脑肌电进行同步性分析并不能准确表达这种传递延迟。

因此,本文提出改进符号化传递熵计算方法,主要从符号化方法和传递熵的计算两个方面进行改进。在符号化方法基础上提出等概率符号化方法,在符号化区间划分时尽可能保留信号的原始动态信息;在传递熵计算基础上提出延时传递熵计算方法,在脑肌耦合分析时加入对脑肌电信号的信息传输延迟的考虑,算法流程如图1所示。

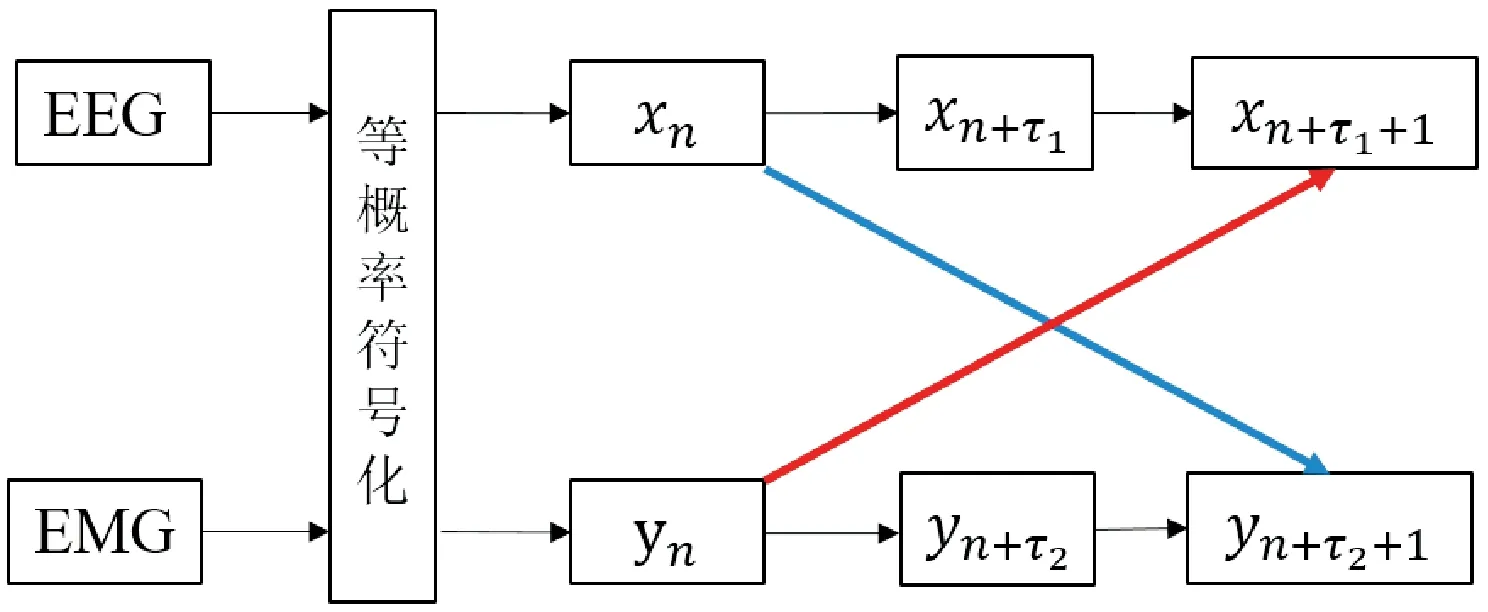
图1 基于延时等概率符号化传递熵的脑肌电信号耦合分析方法 Fig.1 Brain-muscle coupling analysis based on delay equal probability-symbolized transfer entropy

1.1 等概率符号化方法

本文所提等概率符号化方法,使符号化时间序列中各符号的出现概率相同,并可以根据需要动态调整符号数量。从而更好地保留原始时间序列中的信息,具体算法思路如下:对原始时间序列X(n)={x(1),x(2),…,x(n)}由小到大排序,排序后的序列为V(n)={v(1),v(2),…,v(n)};设定一个可变的尺度参数k,k表示需要划分的符号数,则每个符号中对应的采样点数j的计算式为

(3)

式中:round(·)为四舍五入运算。

取区间划分参数

d(k)=v(kj)

(4)

式中:k为1,2,…,k-1。

然后,对原始时间序列X(n)进行符号化,符号化过程的函数形式为

(5)

由于n≫k,因此不必考虑边界点的归属和边界区间极少数据点数差异,可以认为通过等概率划分区间的方法,能够保证每个区间内的数据点数近似相同。

从符号化时间序列包含的信息量角度进行考虑,符号时间序列中包含的信息量可以由香农熵表示,其计算式为

(6)

式中n为符号数量。可知当各个符号的出现概率p(xi)相同时,系统的不确定性和信息量最大。

传统变尺度符号化方法对生理电信号进行符号化可能导致少数几个符号代替大量的观测值,因而其符号化时间序列中的不确定性较低,包含的信息量少,而等概率符号化方法使各个符号的出现概率相同,能够包含原始时间序列中更多的动态信息,同时也具有传统符号化方法降低信号中动力学噪声和测量噪声影响的优点。

1.2 延时等概率符号化传递熵

式(2)描述的方法仅对被预测样本x(n+τ)添加延时参数,这种方式能够一定程度上分析两个时间序列的延迟,但它忽略了序列自身的信息传递,当时间序列间的信息传递延迟远小于时间序列自身内的信息传递延迟时,这种改进传递熵方法并不能去除序列自身的信息传递影响,因而得不到准确的序列间信息传递结果。

本文所提延时等概率符号化传递熵(ETST),对于符号化时间序X(n)={x(1),x(2),…,x(n)}和Y(n)={y(1),y(2),…,y(n)},定义ETST(Y→X)为

ETST(Y→X)=

(7)

式中τ为序列Y(n)到X(n)的信息传递延迟。

按照传递熵的定义,本文定义的ETST(Y→X)的物理意义是已知信号Y和延迟τ后的信号X,去除信号X自身的信息量,信号Y能够对延迟为τ+1的信号X的预测起到较大的作用。

2 脑肌电信号耦合分析实验流程与数据采集

为了验证所提方法的有效性,面向手部功能康复训练中的常用手势——手部抓握运动,开展手部运动过程中的EEG和sEMG信号的实时采集与分析实验。实验共招募了10名无精神类疾病的健康被试,7名男性和3名女性,均为右利手,平均年龄为24岁。所有被试者在实验前均已阅读实验说明并签署了知情同意书。每次实验持续时间为12～17 s,具体流程如下:实验开始,在t=0 s时,屏幕中央以文字提示被试者实验即将开始,被试者得到提示后注视屏幕;以屏幕显示静止的左手和右手,屏幕中心显示注视十字,被试者注视十字并保持静息状态,为排除被试自身节律或时间期待等因素的影响,静息状态持续时间随机地设置为5～10 s;范式随机提示左侧或右侧手部的运动想象任务,屏幕中心十字变为指向左或右的箭头,根据范式提示,被试使用同侧的手与范式进行持续5 s的同步抓握运动,且将抓握力保持在低于20%最大自主收缩的水平;单次任务结束,进入下一次的实验准备阶段。

本实验使用gUSBamp设备同步采集脑电和肌电信号,脑电信号采集选取覆盖运动皮层的脑电通道,具体包括F3、FZ、F4、FC3、FCZ、FC4、C3、CZ、C4、P3、PZ、P4;肌电信号采集两侧手臂的指浅屈肌(FDS)和肱肌(BM)处的肌电信号。

实验要求被试者集中精力想象手部活动,实验要求在安静、微暗的环境下进行,避免外界噪声对被试者造成干扰,实验现场如图2所示。最后获得被试者每侧手部以较小力度抓握时的脑肌电数据,选取每名被试者每侧手部各20个试次,用来研究手部运动过程中大脑运动皮层和运动肌肉间的耦合关系。

图2 脑肌电同步采集实验环境示意图Fig.2 Schematic diagram of experimental environment for synchronous EEG EMG acquisition

3 脑肌电传递延迟分析

对脑电信号进行1～100 Hz带通滤波,以去除高频噪声和低频运动伪迹的影响,然后使用延时等概率符号化传递熵对10名被试者的脑电信号和肌电信号进行分析,以获得被试者的脑肌电间信息传递延迟时间。进行EEG至EMG的传递分析时,本文选使用等概率符号化方式对脑电信号和肌电信号分别进行符号化,设定参数k=10。

根据大脑对躯体的对侧控制机制,选取右手指浅屈肌的肌电信号与C3通道脑电信号进行信息传递延迟分析,左手指浅屈肌的肌电信号与C4通道脑电信号进行信息传递延迟分析,现有研究表明皮层与肌肉的信息流延时大约在20～30 ms左右,因此本文选取1～50 ms延迟时长内的传递信息为分析对象,由此测量每个被试EEG至EMG信息流传递延迟时间,并对每个被试者的实验数据多个试次进行叠加平均,从而完成进一步的观察。其中,被试S1的两侧手部EEG→EMG传递熵随延迟时间变化的分析结果,τ为最优延迟时间,如图3、图4所示。

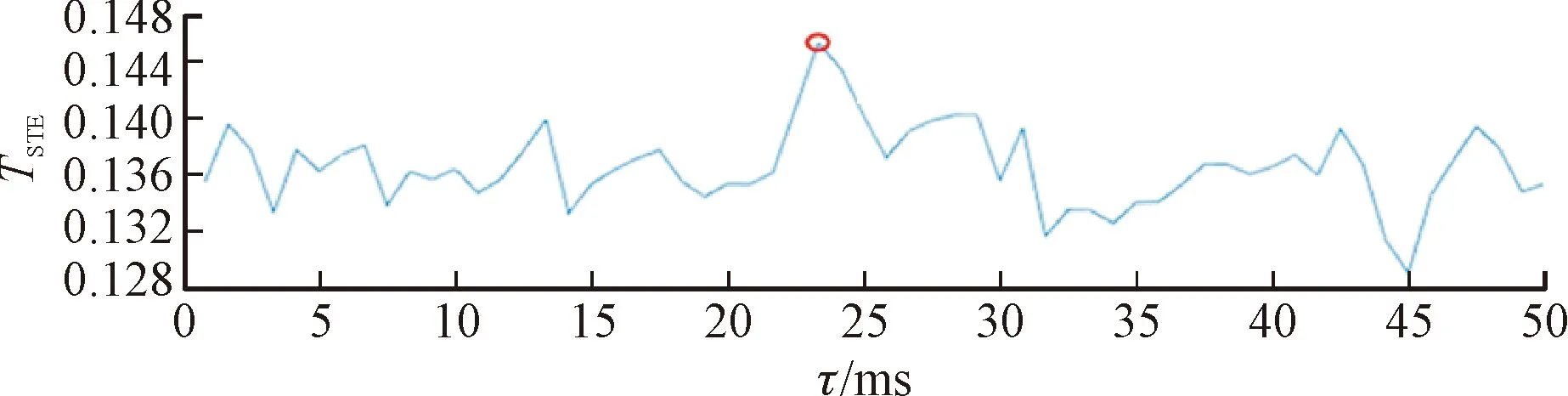
图3 左手EEG至EMG信息传递延迟分析Fig.3 The delay analysis of left hand EEG→EMG information transmission

图4 右手EEG至EMG信息传递延迟分析Fig.4 The delay analysis of right hand EEG→EMG information transmission

可以看到,进行左侧手部抓握时,在延迟时间为23.3 ms时出现传递熵峰值,在该时间延迟下脑电信号与肌电信号间存在最强的单向信息传递,可以认为是肌肉对大脑控制信号的响应延迟。在右手手部抓握时延迟时间为23.3 ms时出现传递熵峰值。

对EMG至EEG的信息传递延迟进行分析时,同样采用C3、C4通道脑电信号与对侧手部的指浅屈肌的肌电信号进行符号化传递熵的分析,结果如图5、图6所示。

图6 右手EMG至EEG符号化传递熵分析Fig.6 The transfer entropy of right hand EMG to EEG information transmission

与EEG至EMG相似,被试S1的左手和右手抓握时EMG至EEG的信息传递延迟分别为29.2、30.8 ms。由于信息传递延迟可能存在一定波动,有的被试者可能出现峰值不显著的情况,例如被试S1的右手EMG至EEG的传递熵峰值相对不显著,但人体的神经传导速度基本确定,在20～35 ms范围内选择峰值最可能符合实际信息传递延迟。记录其他被试者的脑电与肌电的符号化传递熵分析结果,最优延迟时间的分析结果如表1所示。

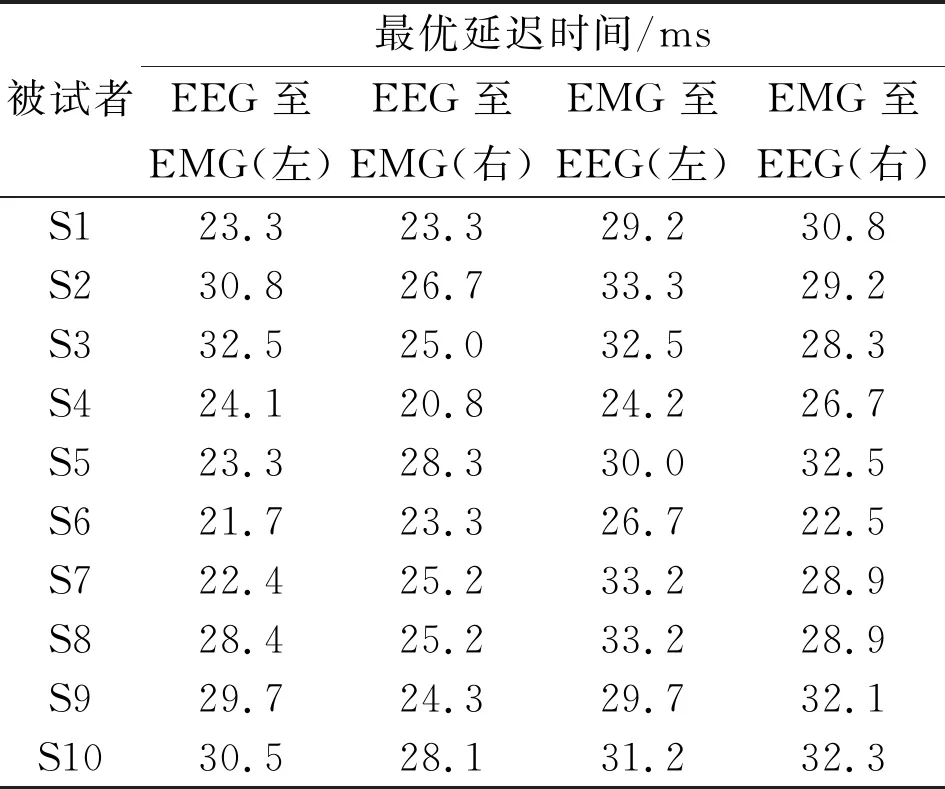
表1 被试者S1～S10的最优延迟时间

由表1可知,在被试群体中,从EEG至EMG方向的最优延迟时间普遍短于从EMG至EEG,且EEG至EMG的延迟时长为21.7～32.5 ms,而EMG至EEG的时长约为24.2～33.2 ms。由于不同被试者之间存在个体差异,其最优延迟时间也存在差异,但该差异仅在毫秒之内,可以忽略不计,实验得到最优延迟时间具有普适性。

4 多通道脑肌电符号化传递熵分析

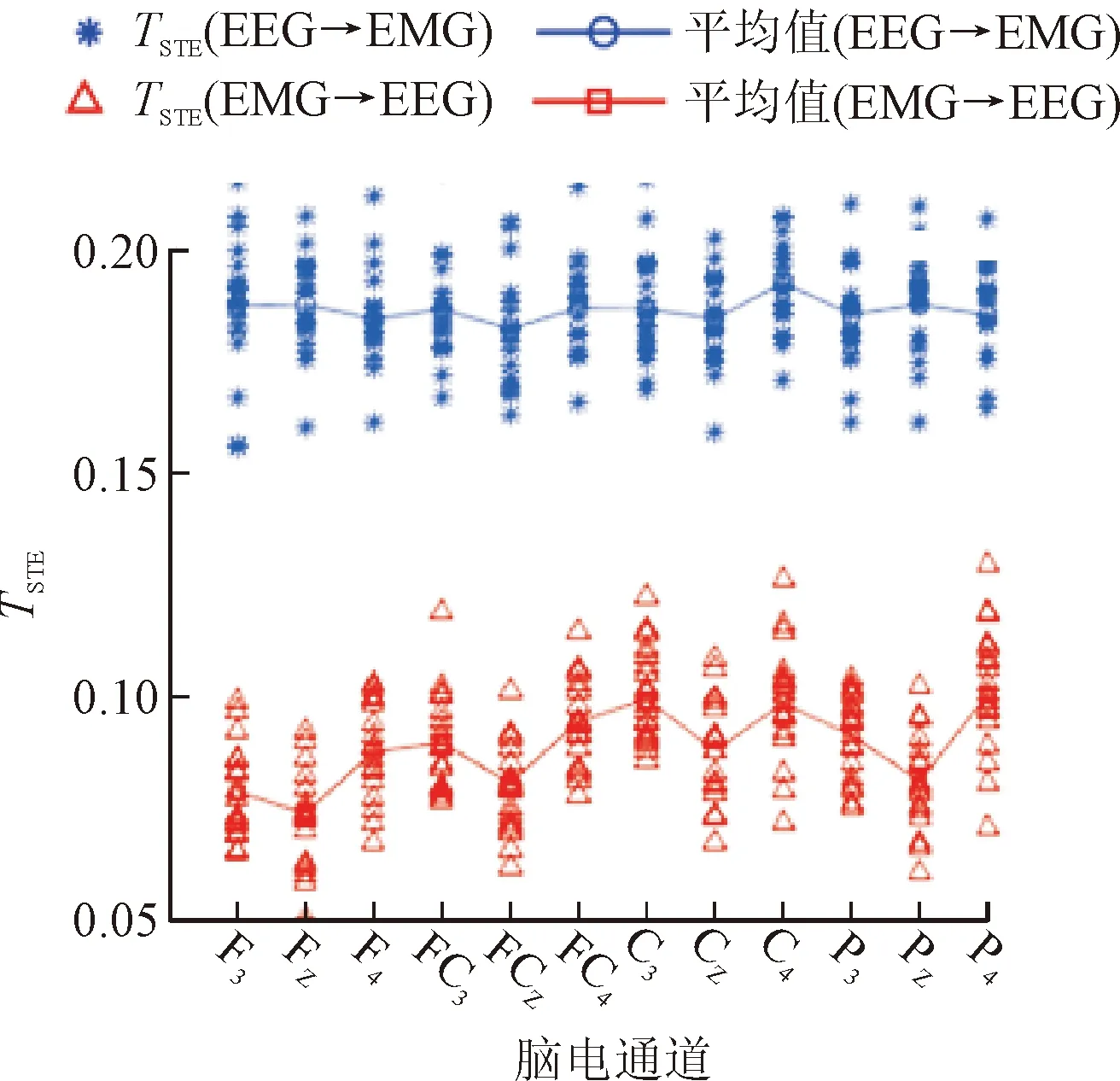
为了分析手部运动过程中上臂肌肉与大脑运动功能区之间的耦合关系,本文对各被试者左、右手进行抓握时运动一侧的指浅屈肌肌电信号与各导联脑电信号和进行延时等概率符号化传递熵进行分析,延迟τ使用表1中确定的最优延迟时间,以被试S1为例,被试S1的延时等概率符号化传递熵分析结果如图7所示。

(a)左手

(b)右手

由图7可以发现,左侧手部抓握时,C4通道的脑电信号与左手指浅屈肌的肌电信号存在最强的单向(EEG至EMG)信息传递,并且左手指浅屈肌的肌电信号与P4通道的脑电信号存在最强的单向(EMG至EEG)信息传递。右侧手部抓握时,C3通道的脑电信号与右手指浅屈肌在两个方向上的信息传递均是最强。对其他被试者的脑肌电符号化传递熵的分析也呈现类似的结果,例如对于被试S3,其左手和右手进行抓握时EEG至EMG方向信息传递最强的脑电通道分别为C4、FC3,这也恰好符合大脑的对侧控制机制,实验表明本文改进符号化传递熵能够分析出脑电和肌电间的双向信息传递关系,从而体现手部肌肉与大脑的运动皮层的双向耦合关系。

同时可以观察到脑电到肌电的延时等概率符号化传递熵显著高于从肌电到脑电,从因果性的角度分析,可以认为脑电是因,肌电是果,主要的信息传递是由脑电到肌电。这与一般认知是相符的,当肢体运动发生时:一方面,大脑的运动皮层会发出信号,沿着运动传导通路下行传导至肢体的神经和肌肉;另一方面,本体感觉信息通过运动感知传导通路上行传导至大脑的运动感觉区域,大脑对感知到的运动信息加以分析后发出调节运动的指令,大脑在运动调控中起主导作用。

5 运动过程中的符号化传递熵变化分析

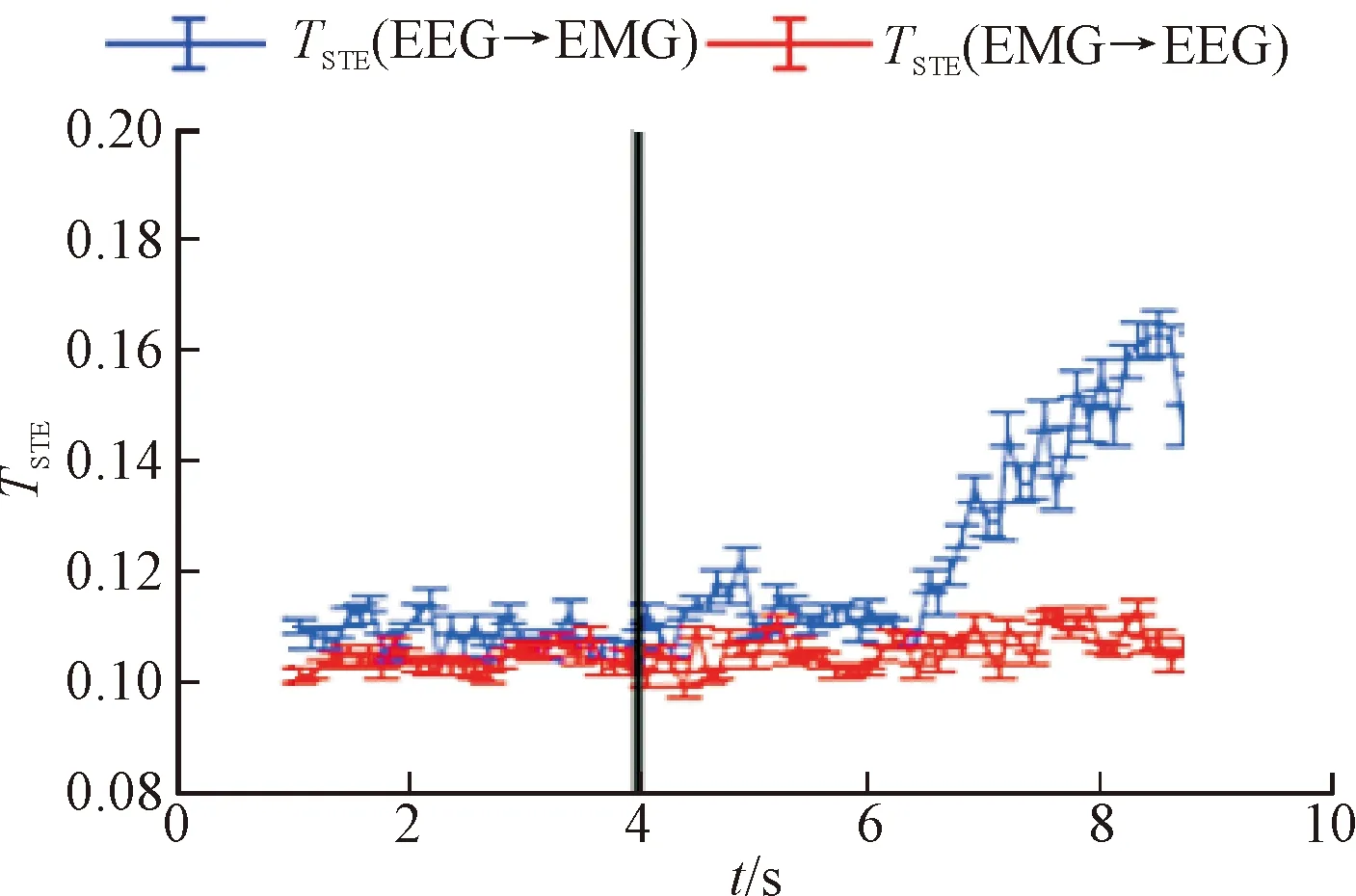
为了研究运动执行过程中的脑电和肌电的耦合强度变化情况,本文分析了静息态到运动态的脑电及肌电信号符号化传递熵变化。具体步骤如下:选取多通道脑肌电耦合分析中得到的信息传递最强的脑电和肌电导联的数据,进行去噪和1～100 Hz的带通滤波处理;对单个试次的脑肌电数据进行分析,从单个试次静息态开始,以1 s的时窗,以0.1 s间隔滑窗截取信号,分别对每段数据计算EEG至EMG和EMG至EEG的在表1中确定的最优延迟时间下的延时等概率符号化传递熵,构成符号化传递熵随时间的变化曲线;分别对左右手的20个试次的符号化传递熵随时间的变化曲线进行叠加,计算均值和方差,得到每个被试者左手和右手在抓握时的符号化传递熵变化曲线。对于被试S1和S2手部抓握过程的平均符号化传递熵分析结果如图8所示,图8中方差为实际计算结果的1/10。

(a)被试S1左手

(b)被试S2左手

(c)被试S1右手

(d)被试S2右手

图8中黑色竖线表示屏幕提示被试者开始手部抓握运动的时刻,可得如下结论:在提示被试者开始手部抓握动作前,脑电与肌电信号的传递熵幅值均较低,EEG至EMG的符号化传递熵值仅略高于EMG至EEG,说明二者并未表现出直接的因果关系,且静息状态时大脑皮层与手部肌肉间的信息传递较少;在提示被试者开始手部动作1～2 s后,被试的EEG至EMG符号化传递熵值有显著上升趋势,在运动结束后上升趋势逐渐消失;被试者EMG至EEG的符号化传递熵值有一定上升趋势,但幅度较小,不如EEG至EMG的变化明显,能够说明在手部主动运动时,大脑皮层向肌肉发送调控指令,从而引起肌肉的活动,肌肉活动也会通过上行的通道向大脑皮层发送感知反馈信息,从而引起肌电到脑电方向的耦合强度上升;在两侧手部均使用较小抓握力度的情况下,各被试者右手EEG至EMG的符号化传递熵值要明显高于左手,推测是由于本文被试者均为右利手,右手肌肉与大脑皮层的耦合性更强,一定程度上说明了本文符号化传递熵方法能够较好地分析出脑肌耦合强度。

综上所述,本文改进符号化传递熵方法可以分析大脑皮层和运动肌肉间的双向信息传递,能够体现脑肌耦合的时间延迟和耦合强度。经过分析,在人体手部以较小力度运动时时EEG至EMG方向的信息传递要高于EMG至EEG,并且不同方向上主动运动时的耦合强度均高于静息状态时。这可能能够作为识别运动是由患者主动发起还是由于被试者的手部肌肉痉挛或其他症状引起的病态运动的依据,对于临床康复训练有一定的价值。

6 结 论

本文围绕人体手部抓握运动过程中脑肌电神经信息的耦合规律开展研究,提出了延时等概率符号化传递熵分析方法,通过在线实验同步采集手部运动任务中的EEG与EMG信号,进行了手部抓握过程中脑电信号和肌电信号间的双向神经信息传递延迟检测,开展了多通道的脑肌电耦合过程中的功能区定位与强度变化分析。通过延时等概率符号化传递熵对采集得到的EMG与EEG进行分析,可以得到如下结论。

(1)等概率符号化方法使各个符号的出现概率相同,能够包含原始时间序列中更多的动态信息,可以更加精确的脑肌电信号的耦合特征,延时化的传递熵能够有效能够准确地检测到两个时间序列间信息传递,更能准确定位其信息传递延迟,在两个序列间不存在信息传递时计算结果也保持了较好的鲁棒性。

(2)通过对人体手部抓握运动的脑肌电信号进行分析,得到人体左右手的脑肌信息传递具有不对称性,且该传递时延约为20～35 ms。左侧手部抓握过程,C4通道的脑电信号与左手指浅屈肌的肌电信号存在最强的单向(EEG至EMG)信息传递,而右侧手部抓握时,C3通道的脑电信号与右手指浅屈肌在两个方向上的信息传递均是最强,且从脑电到肌电的传递熵峰值显著高于从肌电到脑电的,指明了大脑在运动调控中起主导作用。同时,运动执行任务过程中,脑肌电耦合强度的变化规律表明了不同方向上主动运动耦合强度均高于运动静息状态。

综上,本文不仅提出了全新的脑肌耦合分析技术方法并证明了该方法的有效性,同时揭示了抓握运动过程大脑皮层和手部肌肉的神经作用机制与双向耦合关系,为新的康复方案和康复评价方法提供了理论依据,为神经接口技术的发展提供有力的算法支撑。