拉杆转子接触界面参数识别和动力学研究进展

李浦,袁奇

(西安交通大学叶轮机械研究所,710049,西安)

拉杆组合式转子具有刚度大、重量轻和便于布置冷却通道等优点,被广泛应用于燃气轮机和航空发动机。与整体转子不同,拉杆转子接触界面多,接触状态复杂,工作在高温、高压、高转速环境。据统计,燃气轮机转子系统的故障率占比高达45%,运维费用占整个电厂的60%以上[1]。因此,结构可靠性和完整性对机组安全、稳定运行具有决定性作用。拉杆转子的设计主要考虑以下因素:压气机和透平部分的通流形状、叶片安装及叶片承受的载荷、冷却和密封气体流道的布置、额定载荷和故障状态下传扭的可靠性和结构完整性等。

深入开展螺栓连接拉杆转子的动力学机理研究,是重大装配体可靠性的重要支撑,但对于螺栓连接拉杆转子的固有频率和动力学特性研究,目前并没有给出统一的设计准则。由于多组合界面非线性行为受激振力和运行状态的影响,需要考虑几何结构、界面参数不确定性和多支撑边界条件等因素,因而导致传统的正向分析无法准确预测结构的模态特性和动力学响应。有限元模型修正理论广泛应用于工程技术领域,线性模型修正理论经过多年发展已日趋成熟,但作为线性理论的重要推广,非线性参数识别和模型修正目前尚处于起步阶段。近年来,非线性参数识别技术已成为燃气轮机和航空发动机建模的重要方法之一,例如普惠公司在MIT燃气轮机实验室建立双转子涡扇整机实验平台[2],开展了转子模态参数和气动阻尼识别研究。

针对接触界面建模、模态试验和参数识别,学者们开展了大量的研究工作。从转子设计角度出发,如要保证转子的结构完整性,预紧力是一个关键参数。本文主要讨论了拉杆转子接触界面参数识别和转子动力学特性方面的研究进展,首先总结了燃气轮机拉杆转子结构完整性方面的研究结果,包括转子结构、端面齿连接和完整性分析等;其次归纳了接触界面刚度分析模型;然后,介绍了非线性参数识别方法并总结了拉杆转子接触参数识别的相关研究;最后,讨论了拉杆转子动力学的研究成果和拉杆预紧力设计方法,并展望了未来的研究方向。

1 拉杆转子结构完整性

重型燃气轮机常用于发电领域,可认为是大功率工业燃气轮机。另一种常用的燃气轮机由航空发动机改型而来,称为航改燃气轮机,常用于舰船和机车驱动。与重型燃气轮机相比,航改燃气轮机的效率相对较高,结构紧凑且功率密度大。

1.1 拉杆转子结构特点

根据拉杆的布置结构,重型燃气轮机转子可分为周向拉杆和中心拉杆转子,如图1所示。周向拉杆转子采用周向均布的多拉杆预紧连接,如美国通用公司、日本三菱重工等企业的燃气轮机均采用此结构。中心拉杆转子采用一根拉杆将整个转子轮盘预紧,如德国西门子公司的燃气轮机采用此结构。2种转子结构的对比如表1所示,中心拉杆转子采用端面齿轮盘传递扭矩,拉杆预紧力大,位置在轮盘中心,温度相对较低,且沿轴向布置有阻尼元件,可调节拉杆振动频率以避免共振;周向拉杆转子采用带凸台的多拉杆结构,拉杆温度相对较高,轮盘采用平面摩擦或端面齿盘传递扭矩。

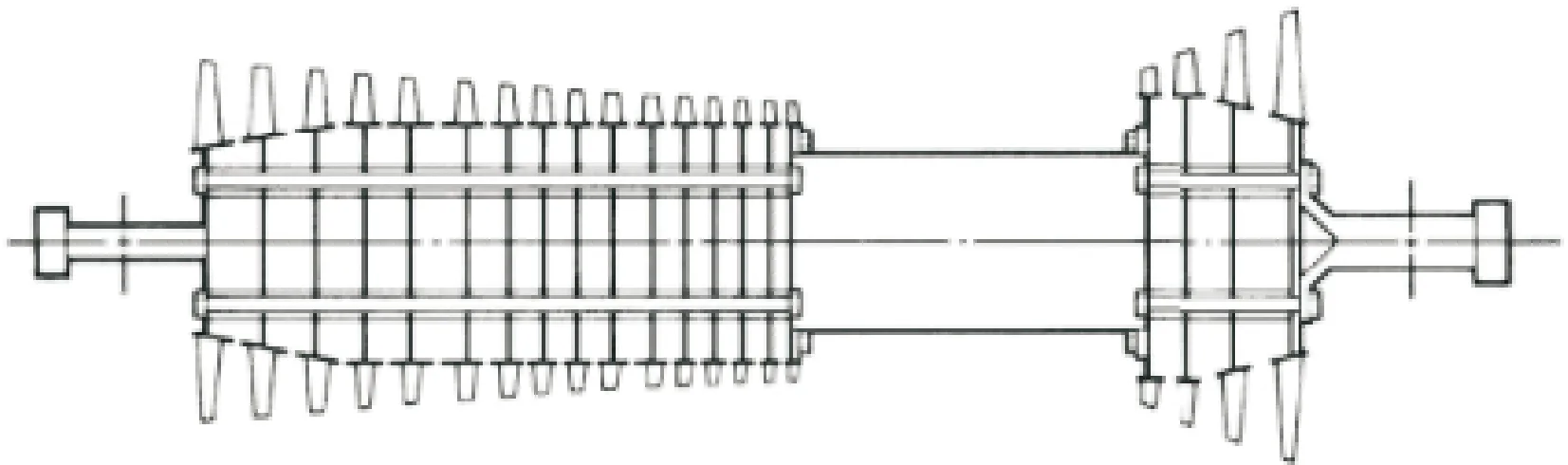
(a)周向拉杆转子

(b)中心拉杆转子

表1 中心拉杆和周向拉杆转子结构对比

1.2 端面齿连接结构

根据传扭方式,拉杆转子的连接结构可分为平面摩擦传扭和端面齿传扭。端面齿盘具有自定心和传扭大等优点,因此在重型燃气轮机和航空发动机中得到广泛应用,例如三菱公司M701F重型燃气轮机的透平轮盘采用弧形齿(Curvic coupling)传扭,西门子公司V94.3A重型燃气轮机的压气机和透平轮盘均采用平面齿(Hirth coupling)传扭。通用、西门子和三菱重工等厂商的F和H级重型燃气轮机拉杆转子盘轴的连接方式如表2所示。端面齿盘连接的可靠性更高,但齿形结构不可避免地会引入应力集中,齿面微动滑移非线性更加复杂,且对齿面加工精度的要求更高。

表2 重型燃气轮机拉杆转子典型连接方式

端面齿结构紧凑且刚性大,被广泛应用于传动装置。由于全齿啮合精度高,也可作为分度装置。根据齿面形状可将端面齿分为平面齿和弧形齿,其加工示意见图2,特点对比汇总于表3。平面齿最早由Albert Hirth于1928年提出[3],主要用于机械传动,通过侧铣刀加工齿面,加工刀路铣削角γ导致齿形向心收缩。弧形齿为格里森(Gleason)公司发明,由一对曲率相同的凹齿和凸齿啮合组成,采用成形砂轮或齿盘在专用磨齿机床上加工,得到要求的齿形齿面,弧形齿主要用于航空发动机以及燃气轮机(如三菱公司)盘轴连接。

(a)弧形齿

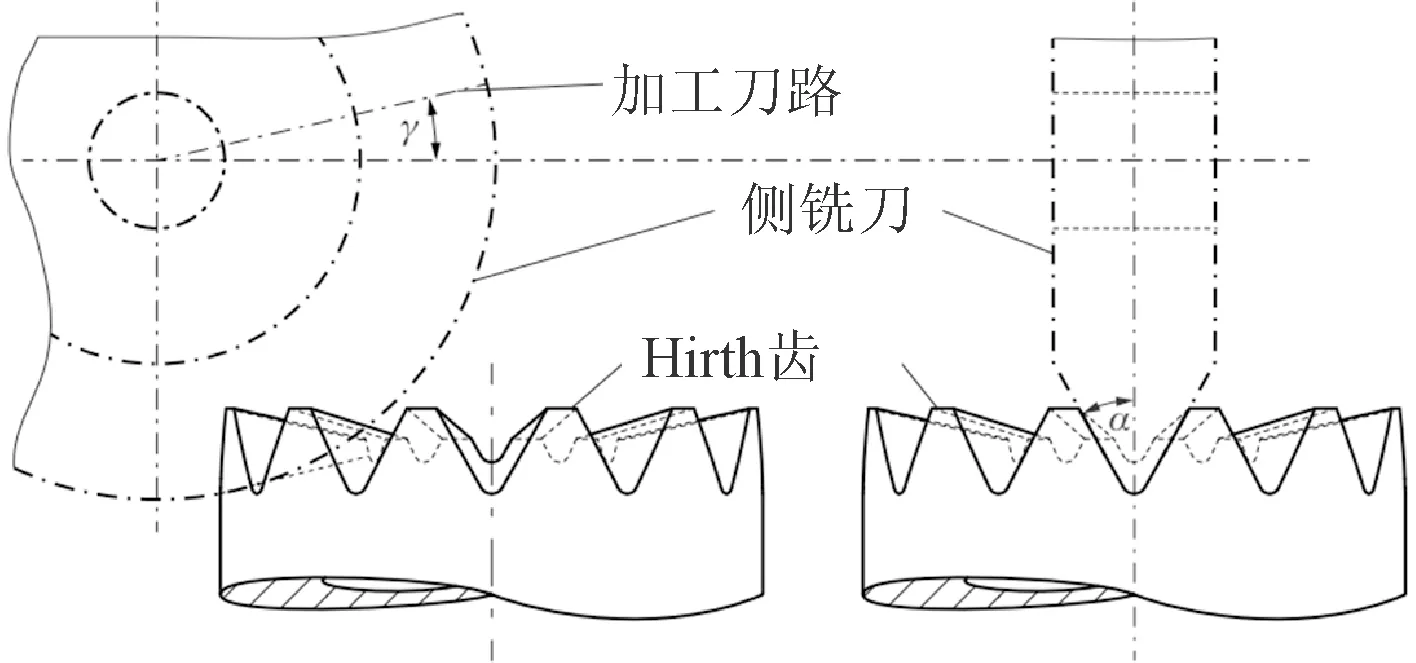
(b)平面齿

表3 平面齿和弧形齿特点对比

1.3 结构完整性分析

燃气轮机结构完整性主要是指在热结构载荷和氧化腐蚀环境下,燃气轮机强度、变形、振动和疲劳等特性能够满足设计要求[4]。拉杆转子动力学是结构完整性的重要研究内容之一,多接触界面诱发的非线性特征往往会导致振动异常甚至结构失效,因此结构完整性是保证其功能性的重要前提。从部件角度而言,需要对压气机叶片、透平叶片、转子和气缸等部件分别开展完整性分析。

拉杆转子界面接触刚度随着预紧力的增加而增加,当预紧力达到一定程度时,拉杆转子模态特性和整体转子保持一致,此时称为预紧饱和状态,可采用转子动力学的常规线性方法进行等效分析。随着高温、高转速、大扭矩燃气轮机的发展,拉杆预紧力在复杂载荷下无法保证接触界面的连续性,不同转速下转子可能出现幅值突跳的“双稳态”现象。拉杆在热疲劳和热腐蚀的耦合作用下产生应力松弛和裂纹,可能会导致整机振动甚至结构失效,例如某工业燃气轮机的中空连接扭矩套筒螺栓在高温和拉扭耦合载荷下曾发生了疲劳断裂[5]。

图3展示了拉杆转子结构完整性分析的具体内容,并梳理了本文的思路。结构完整性分析主要包括结构强度分析和动力学分析两方面,结构强度分析包括静强度分析、蠕变分析和疲劳寿命分析等,动力学建模是动力学分析的基础,包括轴承基础建模和转子部分建模。本文在第2章讨论了基于接触刚度的跨尺度接触界面模型对拉杆转子动力学特性的影响;在第3章总结了不确定非线性边界条件下,基于模态试验的用于确定螺栓连接结构和动力学响应的参数识别方法;第4章主要分析了线性和非线性转子动力学模型和相关研究成果;在第5章讨论了拉杆转子的预紧力设计。

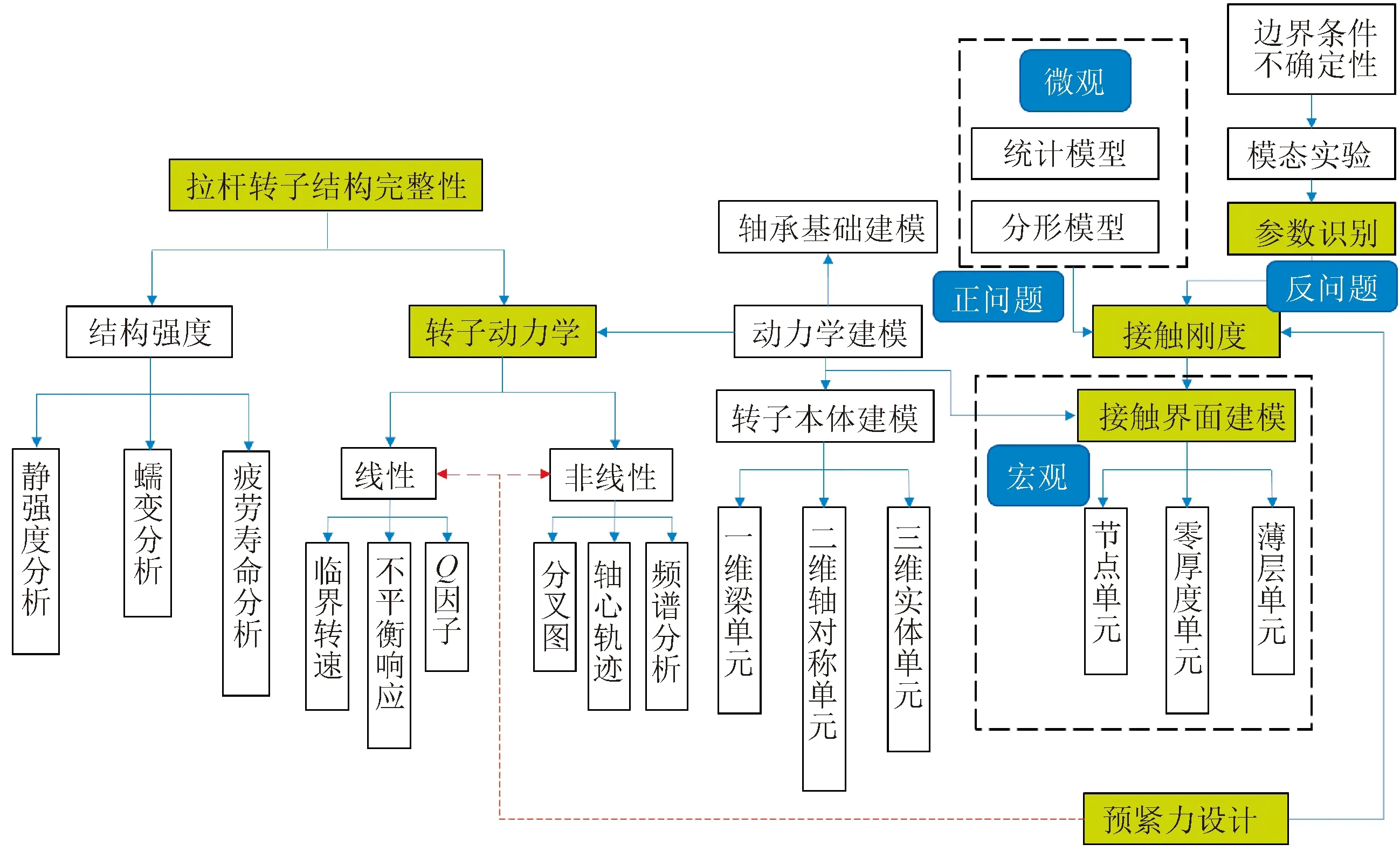
图3 拉杆转子结构完整性分析框图Fig.3 Mechanical integrity analysis of tie-bolt rotors

2 接触界面特性研究

2.1 接触刚度模型

由于机加工表面在微观上具有粗糙形貌,导致两轮盘的实际接触面积小于名义接触面积,因此拉杆转子的刚度可认为是由转子基体刚度和接触层刚度两部分串联而成。不同于连续基体结构,接触刚度呈现出频响函数随预紧力和激振力变化的非线性特征。因此,接触刚度分析是拉杆转子精确建模和动力学响应计算的基础,一般可分为正问题和反问题。正问题即基于微观接触模型建立接触刚度和预紧力、微观形貌参数以及材料参数的关系,反问题即通过模态试验识别接触界面参数。

针对粗糙表面微凸体接触,理论分析模型主要可分为统计学模型和分形模型[6]。赫兹(Hertz)接触给出了刚性球体与弹性平面之间接触压力、渗透量和接触半径的表达式,是接触力学模型的基础[7]。Archard指出平面弹性接触面积和压力近似成正比关系[8]。Greenwood和Williamson等基于统计学理论,指出粗糙面微凸体服从高斯函数假设,并建立了两平面弹性接触(GW)模型,将Hertz接触模型扩展到平面接触[9]。Pullen和Williamson研究了粗糙面塑性接触的表面力学行为[10]。Chang等基于微凸体体积守恒理论,构建了粗糙表面的弹塑性接触(CEB)模型,并通过塑性指数对弹塑性变形进行定量化分析[11],从而建立了联系微凸体弹性和塑性接触的桥梁。Zhao等采用对数函数和多项式函数发展了微凸体的微接触模型[12-13]。

分形模型假设粗糙接触面具有自仿射分形特征,利用分形粗糙度和分形维数描述接触特性。Mandelbrot等提出了用分形参数表征金属表面的分形特征[14]。针对粗糙面接触的多尺度效应,Majumdar和Bhushan指出微凸体尺寸服从幂律分布[15],并建立了弹塑性接触分形(MB)模型,揭示了接触压力、接触面积和分型参数之间的关系[16]。Yan和Komvopoulos基于两变量Weierstrass-Mandelbrot函数,建立了粗糙接触面的三维形貌模型,并用于弹塑性力学分析[17]。张学良等建立了具有尺度独立性的接触刚度和切向刚度分形模型[18-19]。Pohrt和Popov采用边界元法分析了法向接触刚度和分形参数的关系[20]。Zhang等基于接触界面参数识别方法,建立了接触刚度和分形参数的理论模型,并和Pohrt-Popov接触刚度模型进行了对比分析[21]。

综上所述,统计学模型基于微凸体高度概率密度函数,能够描述刚度和阻尼能量耗散特性,但微观形貌特征与采样长度和仪器分辨率有关;分形模型根据分形参数建立了微凸体接触面积分布密度函数,也能够得到界面刚度和阻尼能量耗散特性,但并非所有的接触表面都具有分形特征。

2.2 拉杆转子接触界面建模

开展拉杆转子模态和动力学特性分析,需要先构建微观接触刚度与宏观弯曲刚度和扭转刚度之间的关系,即考虑接触界面的拉杆转子模型。饶柱石和夏松波等采用刚度修正的传递矩阵法,对拉杆转子进行了模态分析[22]。Kim等针对发电机组合转子,研究了预紧力对刚度的影响,提出了预紧饱和概念[23]。王艾伦等采用键合图法对拉杆转子的刚度进行了理论分析[24-25]。

近年来,有限元模型被广泛应用于转子动力特性分析,主要包括一维梁单元、二维轴对称单元和三维实体单元等,其中一维梁单元需要对转子进行简化,二维轴对称单元和三维实体单元可实现CAD和有限元分析的直接转换。针对接触界面的模型单元主要有3种:节点接触单元、零厚度单元和薄层接触单元[26]。节点接触单元在接触节点之间建立了一个等效的弹簧阻尼单元,以表征接触刚度的影响,适合模拟一维梁单元接触效应。对于面单元接触,需要界面节点一一对应,如果考虑所有节点的非线性刚度,瞬态计算将非常耗时。何鹏等基于GW模型,得到了采用集总铰链表征的等效刚度,并建立了拉杆转子的一维有限元模型[27]。Gao等基于GW模型建立了考虑弯矩和轮盘分离故障下的弯曲刚度[28],通过扭转弹簧考虑轮盘接触刚度,并基于一维耦合有限元单元开展了转子模态试验和数值分析,试验实物图如图4所示。

图4 拉杆转子模态试验实物图[28]Fig.4 Modal experiment of a bolt-fastened rotor[28]

零厚度单元是一种等参数接触单元,通过形函数和节点位移定义接触法向刚度和切向刚度矩阵,最早用于地质力学中的岩石耦合模型[29]。Oh等基于GW模型构建了接触刚度和应力分布之间的关系,提出了一种考虑接触刚度的预应力模态分析方法[30]。Balaji等采用零厚度单元法建立了螺栓连接的多尺度非线性模型,将其用于螺栓搭接结构的非线性模态分析[31]。薄层接触单元(也称虚拟材料法)是在接触面之间构建一个薄实体单元,通过接触层的线性本构关系考虑接触刚度对系统的影响。Yao等针对航空发动机螺栓连接结构,提出了一种改进的薄层接触单元,通过分区域修正接触刚度提高了模型精度[32]。Ma等基于薄层单元建立了螺栓法兰连接转子的有限元模型,并采用区间法开展了转子不确定性分析[33]。Du等基于分形接触模型和虚拟材料法开展了拉杆转子模态分析和动力学分析[34]。Rimpel等提出了一种虚拟薄层的弹性模量修正方法,通过拉杆转子模态分析进行验证,并用于某离心压缩机的中心拉杆转子试验,如图5所示[35]。研究表明,接触面止口配合会引起接触状态改变,导致测量模态频率发生阶跃变化。赵润超等根据转子接触特性给出了虚拟材料参数的建模方法,并将其用于动力学特性计算,结果表明预紧力变化对第四阶临界转速的影响达2.31%[36]。

图5 离心压缩机拉杆转子模态试验实物图[35] Fig.5 Modal experiment of a tie-bolt rotor of a centrifugal compressor[35]

相比于平面摩擦接触,端面齿盘广泛用于燃气轮机和航空发动机,是更加可靠的拉杆转子定位和传扭结构。尹泽勇等针对端齿连接转子,采用端齿梁单元开展了转子动力特性分析和轴向预紧力设计研究[37-38]。Yuan等分析了弧形端面齿连接的重型燃气轮机的界面等效刚度,基于弯曲中性层理论推导了节点接触刚度,结果表明端面齿的界面波纹度对转子等效刚度和动力学特性具有显著影响,而对粗糙度的影响较小[39]。Liu等针对弧形端面齿盘结构建立了三弹簧等效刚度模型,并采用三维有限元进行验证,结果表明压力角对端面齿盘接触刚度弱化效应的影响显著[40]。Liu等采用节点单元法模拟了端面齿对的黏滞滑移效应,并对预紧力松弛下的端面齿盘转子进行了数值分析[41]。Yu等考虑了微凸体高度分布标准差、平均半径和接触角等影响因素,基于GW模型分析了端面齿盘接触弯曲刚度,研究表明端面齿盘连接的弯曲刚度要小于平面接触的弯曲刚度[42]。Kim等基于GW模型,构建了三维有限元多尺度迭代接触模型和模态分析流程,开展了端面齿盘模态试验,提出了连接刚度和应力协同分析方法[43-44]。图6展示了Hirth齿盘连接的转子模态试验实物图。

图6 Hirth齿盘连接结构模态试验实物图[43]Fig.6 Modal experiment of a tie-bolt rotor with Hirth couplings[43]

综上所述,采用节点单元法和零厚度单元法可以直接模拟接触界面的非线性特性,但建模相对复杂;薄层单元法采用等效线性模型表征界面非线性特征,有限元建模相对简单,但无法从物理机理层面描述其接触行为。端面齿盘模型一般采用等效梁单元或三维实体单元,多齿面微观弹塑性接触模型的研究还很不充分,多尺度接触刚度和动力学响应的耦合机理更是有待深入研究。

3 拉杆转子接触界面参数识别

3.1 非线性参数识别方法

在“双碳”目标的大背景下,复合材料在燃气轮机和航空发动机转子、机匣等部件应用广泛。由于螺栓连接的拉杆转子结构日趋轻量化和复杂化,非线性在结构动力学的分析中不可忽略。由于材料参数和接触参数的不确定性,一般需要采用非线性识别方法来进行模型修正和确定。非线性系统辨识包括非线性检测、非线性特征描述和参数估计等[45]。Kerschen等将非线性系统辨识方法分为回复力面法(或力状态映射法)、直接参数估计法、非线性自回归滑动平均(NARMAX)模型法、Hilbert变换法、Volterra级数法、模态参数法等[45]。Kerschen等在2017年进一步将识别方法归总为线性化法、时域法、频域法、时频域法、模态方法、黑盒法以及模型修正方法[46]。

非线性参数识别可以分为全局非线性和局部非线性两大类。全局非线性是指大部分结构发生非线性行为,如大载荷引起的结构几何非线性等。局部非线性只是在局部有限范围内发生的非线性行为,其他部分仍然是线性的,大多数螺栓预紧的组合结构都存在局部非线性。对于多自由度动力学系统,Zhang等提出了基于频响函数重构试验的非线性参数识别法,得到了对应线性系统的等效刚度和等效阻尼[47]。考虑非线性力的多自由度动力学方程可表示为

(1)

基于等效刚度和等效阻尼的非线性系统可以表示为

(2)

式中:Keq、Deq分别为参数识别法得到的等效刚度矩阵和等效阻尼系数矩阵。

拉杆转子是一种特殊的螺栓连接结构,国内外开展了大量关于螺栓搭接和螺栓法兰连接的研究工作,螺栓连接跨尺度模型为拉杆转子建模提供了一种研究方法。但是,拉杆转子的静态模态分析不能预测转动下复杂非线性特征,且多种组合接触状态(法向接触、切向止口接触和齿盘接触等)不确定性诱发的转子振动异常现象的机理尚不清楚。

3.2 拉杆转子接触参数识别

相比螺栓搭接结构和螺栓法兰连接,拉杆转子一般具有多对接触面,可能会承受预紧力、不平衡力和扭矩等组合载荷。如图7所示,Zhang等采用均布弹簧模拟接触界面,根据不同粗糙度和预紧力下的模态敲击试验结果,识别和修正了有限元模型的界面弹簧刚度,给出了接触刚度随名义压力的变化曲线,并应用于某实际燃气轮机转子的模态分析[48]。结果表明:透平和压气机轮盘接触刚度在1013N/m3量级,真实燃气轮机拉杆转子融合接触刚度的有限元分析和模态试验结果最大误差为1.14%,证明了所用模型的正确性。

图7 拉杆转子自由敲击模态试验[48]Fig.7 Modal experimental of a rod-fastened rotor under free-free boundary condition using a hammer excitation method[48]

张子阳等提出弹簧刚度矩阵和有限元模型刚度矩阵融合修正方法,分析了航空发动机拉杆转子的接触状态[49]。高进等基于弹簧连接的梁单元建立了拉杆转子模型,采用弹簧线性刚度表征了梁单元的阶梯轴结构突变和接触效应双重刚度弱化,并基于灵敏度分析开展了转子模型修正,如图8所示[50]。

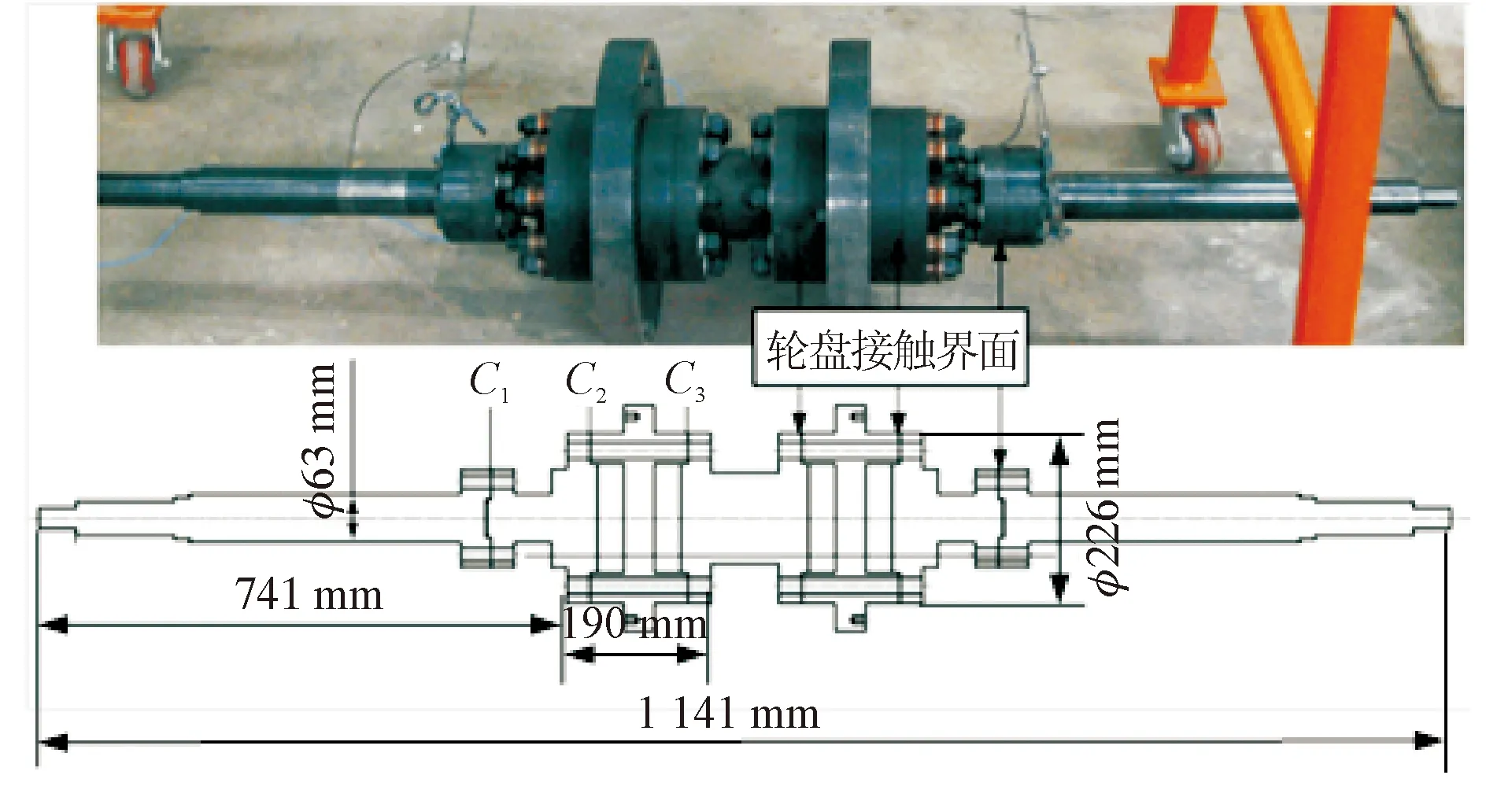
图8 拉杆转子模型修正试验[50]Fig.8 Model updating of a rod-fastened rotor[50]

缪辉等采用薄层单元开展空气循环机拉杆转子界面动力学研究,提出了部件模型修正和连接模型修正的分层模型修正方法[51],基于灵敏度分析选择待修正参数,通过修正分层模型对接触界面连接刚度进行了准确识别,并与试验结果作对比验证了方法的正确性。图9展示了空气循环机拉杆转子模态试验实物图。

图9 空气循环机拉杆转子模态试验[51]Fig.9 Modal experiment of a rod-fastened rotor of an air cycle machine [51]

Li等采用虚拟材料法开展了拉杆转子模态试验分析和接触刚度阻尼参数识别,结果表明:过盈止口连接导致接触刚度随着预紧力的增加呈现双线性特征,由于接触面状态发生改变,接触阻尼在双线性转折点出现了突跳现象[52]。赵广等采用双薄层单元法建立了盘鼓螺栓连接结构的接触刚度模型,并基于模态试验开展了刚度识别研究[53]。Zou等针对高压发动机盘鼓式转子开展了预紧力和接触状态参数识别研究,试验如图10所示,采用力矩扳手控制24个周向均布螺栓预紧力,分别在20%和40%预紧不均状态下,通过敲击试验识别各阶模态频率,结果表明响应频率对于局部螺栓松动的识别灵敏度较低,由此提出了低阶模态相移法和高阶模态响应偏差法的综合识别方法[54]。边涛等采用Hilbert-Huang变换方法对拉杆转子模态参数进行了识别[55]。颜正杰等基于BP神经网络,采用粒子群法对拉杆转子结合面的特性参数进行了优化识别[56]。

图10 高压发动机拉杆转子模态试验[54]Fig.10 Modal experiment of a rod-fastened rotor of high pressure engine[54]

综上所述,针对螺栓连接界面的不确定性,众多学者开展了界面参数识别研究。目前,大多数参数识别研究聚焦于平面连接的螺栓连接结构,针对端面齿盘连接的参数识别研究较少。此外,参数识别大多数基于自由模态敲击试验,通过改变预紧力实现改变接触刚度转子的模态分析。但实际上,非线性转子动力学特性与激振力密切相关,在不同激振力作用下了解转子的响应峰值频移现象和迟滞特性具有十分重要的意义。从数学模型角度而言,由于特征值和特征向量与转子频率和振型相对应,因此分析拉杆转子振动频率的变化趋势需要结合振型特征进行综合评判。

4 拉杆转子动力学分析

螺栓连接的转子-轴承系统动力学建模和振动特性分析,主要包括线性动力学和非线性动力学两个方面,从数值方法角度可分为时域计算和频域计算。线性动力学分析采用线性弹簧耦合接触面节点,或线性薄层单元修正接触刚度,对临界转速和不平衡响应进行分析。高锐等考虑接触面刚度对转子动力学的影响,采用线性铰链单元和一维梁单元对某型重型燃气轮机开展了临界转速分析[57]。Jam等采用一维梁单元建立了某商业燃气轮机中心拉杆转子模型,通过考虑预应力刚度矩阵对预紧力的影响,计算出的固有频率最大误差达10%,说明仅考虑预应力载荷无法准确模拟界面接触对动力学的影响[58]。Wagner等针对某拉杆转子,采用两步法进行拉杆转子临界转速计算,根据静态应力分析确定接触面状态,并通过多点耦合方法(MPC)建立了考虑接触状态的动力学分析模型。与整个界面耦合模型相比,此方法考虑了局部应力不均匀导致的刚度弱化效应,可认为是一种应力-动力单向耦合模式[59]。Xu等在不同预紧力作用下,采用节点单元法推导了拉杆转子的运动方程,计算了转子的弯曲固有频率[60]。

拉杆转子非线性动力学包括界面非线性、轴承参数非线性以及故障(碰摩、不对中等)引起的非线性。钱征文等针对盘式拉杆转子出现的“双稳态”振动问题,将接触刚度等效为非线性刚度的抗弯弹簧,采用谐波平衡法和同伦算法分析了转子的振动特性[61]。Hei等采用三次方刚度非线性弹簧表征接触刚度,建立了拉杆转子-滑动轴承系统的动力学模型,并基于Newmark方法开展了非线性动力学分析[62]。Hu等考虑油膜力、不平衡载荷以及拉杆预紧力等因素影响,建立了周向拉杆转子的运动微分方程,并采用Runge-Kutta法进行数值求解,分析了转子在不同参数下的非线性响应[63]。Li等针对多盘拉杆转子定点碰摩,采用直接数值积分法开展了非线性振动分析,研究了不同碰摩位置下的转子动态响应[64]。Liu等采用三维有限元缩减模型,分析了界面加工误差对拉杆转子动态响应和稳定性的影响规律[65]。Wang等基于三维有限元模型分析了裂纹对拉杆转子动力学特性的影响[66]。金淼等针对端面齿预紧的拉杆转子,基于梁单元模型建立了中心拉杆-转子-叶片耦合系统动力学分析模型,并进行了临界转速和不平衡响应分析[67]。Wang等分析了拉杆转子轮盘之间的内阻尼对转子动力学响应和稳定性的影响,指出内阻尼会减小失稳阈值转速[68]。Liu等针对拉杆裂纹故障,引入裂纹修正系数来描述拉杆松动,通过建立时变刚度矩阵,研究了周向拉杆裂纹对转子非线性动力学性能的影响[69]。Zhang等基于集总参数法和立方非线性刚度建立了双盘拉杆转子轴承系统的动力学方程,并采用数值积分法分析了多参数对非线性特性的影响[70-71]。Hong等考虑螺栓松动引起的残余预紧力,提出了一种新的非对称螺栓预紧力的呼吸模型,通过建立转子参数机理分析模型,研究了不对称残余预紧对航空发动机组合共振的影响,并采用某实际双转子进行了试验验证[72]。王奇等针对拉杆预紧不均引起的振动局部化现象开展了理论研究,提出当激振频率位于一定频段内时,振动能量在局部集中从而诱发了振动局部化现象[73]。罗忠等总结了组合支承转子系统模型建模法、高维降维法、非线性动力学微分方程求解法、组合支承非线性问题等对转子系统振动特性的影响机理,指出了组合支承转子系统研究中值得关注的问题[74]。

综上所述,近年来针对拉杆转子的动力学分析主要集中于故障引起的非线性特性,如碰摩、拉杆松动和突加载荷等,具体分析方法可分为时域和频域两种,如直接数值积分法和谐波平衡法。相比于一般的线性转子动力学分析,由于非线性分析计算耗时严重,一般采用一维梁单元或三维缩减模型对拉杆转子进行简化;对于拉杆松动、动压油膜润滑轴承等引起的非线性力,一般采用等效模型进行处理。

5 拉杆转子预紧力设计

复杂边界条件下,拉杆转子的动力学响应一般都是非线性的。对于大多数重型燃气轮机转子,只要拉杆预紧力足够大,就能保证转子在运行转速范围内始终处于接触状态,但预紧饱和并无统一的量化标准。对于航空发动机转子,由于频繁变工况运行,大量螺栓连接结构呈现复杂的非线性特征,因此拉杆预紧力是拉杆转子十分重要的设计参数之一。

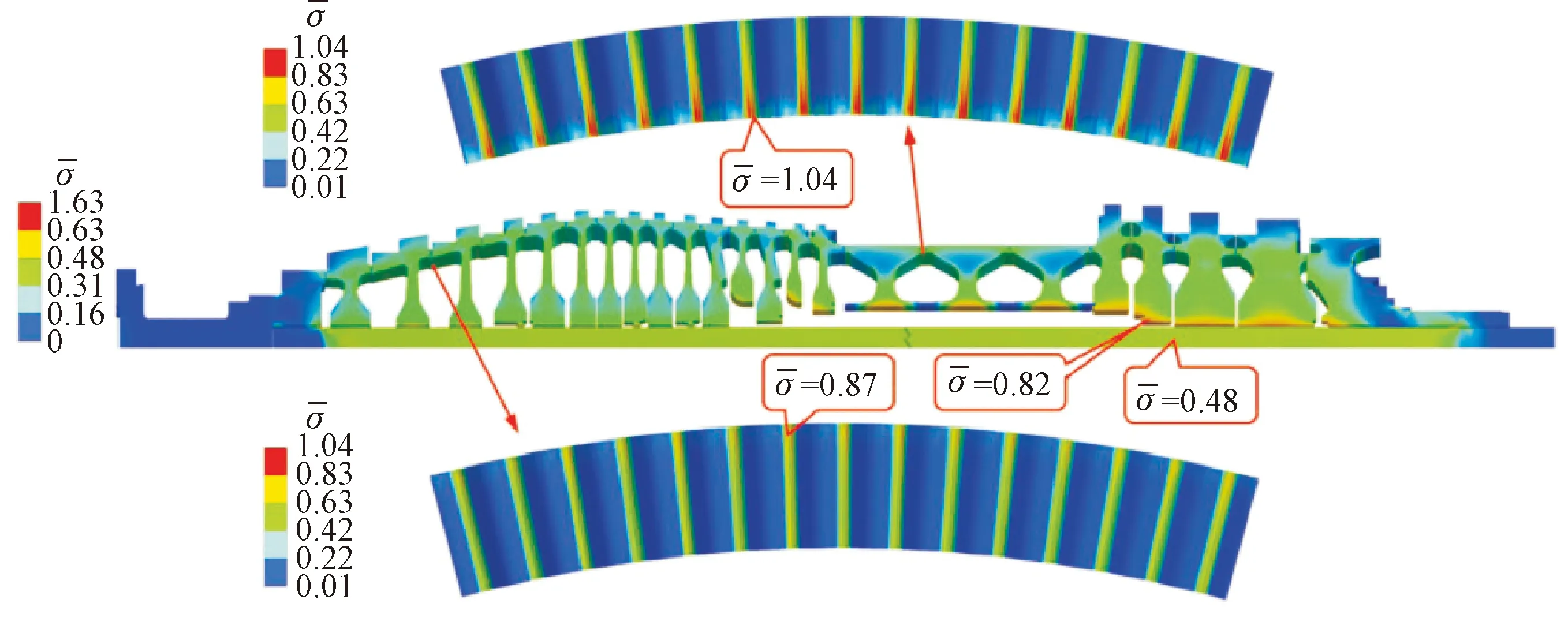
图11 F级拉杆转子稳态运行应力分布图[76]Fig.11 Stress distribution of a F class gas turbine tie-bolt rotor under steady state conditions[76]

典型商业燃气轮机轮盘预紧力名义压力如表4所示[77]。可以看出,预紧力下的名义应力高达数十甚至上百兆帕,并没有一个统一的标准。对于重型燃气轮机,工程中一般将无量纲预紧力,即预紧力与轮盘自重所引起的弯曲产生的轴向脱开力比值,作为设计准则。为了保证轮盘不脱离,无量纲预紧力应大于1。考虑一定的安全裕度,实际工作中燃气轮机的无量纲预紧力应保证在4～8之间。此外,预紧力设计还需要考虑转子传递扭矩的能力。随着预紧力增加,转子能够传递更大扭矩,但接触应力增大会带来强度问题[78]。对于航空发动机转子,由于重量小且大多为鼓筒薄壁结构,多螺栓预紧的不确定性和大载荷的残余预紧力更易诱发转子产生非线性振动。

表4 典型F级重型燃气轮机转子接触界面名义压力

6 总结与展望

拉杆转子作为燃气轮机和航空发动机的重要旋转设备,了解其界面接触状态和动力学响应的耦合机理,对整机动态性能的预测和可靠性分析具有重要意义。拉杆转子结合界面主要包括平面接触和端面齿盘连接两种类型,还需考虑止口、拉杆孔等配合面的接触状态。从宏观角度而言,拉杆转子可认为是一种螺栓连接的装配体。针对平面接触的拉杆转子,如何提升和保证装配界面接触压力的均匀性,以及如何减小应力集中,是解决整机振动和零部件疲劳失效的关键所在。端面齿盘具有定位准确和传扭可靠等优点,但同时也引入了新的挑战和问题:①齿形结构决定了其固有的应力集中现象,无法保证界面应力均匀;②齿盘接触刚度需要综合考虑齿面微观形貌特征和宏观齿形参数;③齿面非对称接触下的黏滞-滑移现象更加复杂;④对弹性耦合的多齿对开展接触分析,需要兼顾模型精度和计算耗时。

随着高温、高转速、变工况发动机的发展和轻型复合材料的广泛应用,螺栓连接多接触界面的非线性接触刚度和阻尼特性对结构动力学响应的影响越发明显。基于模态试验的参数识别是多组合体精确建模的重要方法之一。对于螺栓搭接和法兰连接结构,国内外学者开展了深入的理论分析和试验研究,但其本构模型和计算结论无法直接应用于燃气轮机拉杆转子的动力学分析。这是因为,拉杆转子的边界条件十分复杂,需要考虑诸如高温、高转速、变工况下等环境下的拉杆残余预紧力和响应的动态耦合。另外,拉杆转子的结构和连接状态也非常复杂,如多级轴流式转子法向平面接触、切向止口定位和端面齿盘等多接触面之间的耦合关系,并非简单的螺栓板状搭接结构能够反映。综上所述,可归纳出以下有待解决的问题。

(1)针对拉杆转子微观形貌到宏观动力学跨尺度问题,有必要建立更为准确可靠的本构模型和参数映射关系,尤其是对于端面齿连接结构,需要综合考虑宏观齿形结构和微观形貌特征,用以阐明多尺度协同作用机理。

(2)针对不同边界条件下模型非线性界面参数的不确定性开展模型参数识别研究,建立不同激励水平下的非线性响应变化关系。随着深度学习技术的快速发展,数据驱动的动力学建模方法和参数识别,为拉杆转子精确建模提供了新的思路和方法。

(3)开展多物理场耦合的拉杆转子非线性动力学分析,需要兼顾计算效率和精度。考虑建立描述拉杆转子动力学性能的降阶模型和协同仿真数值计算方法,为复杂转子动力学分析提供可能。

(4)考虑拉杆预紧失谐和装配界面典型故障,建立不同结构参数和运行工况下的转子饱和预紧力设计准则,为转子界面的加工和装配工艺提供理论指导。