分接开关快速机构时变运动可靠性与灵敏度分析

段金燕,赵强强,汪可,李戈琦,张进华,洪军

(1. 西安交通大学机械工程学院,710049,西安; 2. 西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安; 3. 中国电力科学研究院有限公司,100192,北京)

快速机构是特高压换流变有载分接开关的关键部件之一,通过能量的储存与释放,带动有载分接开关运动,从而使换流变阀侧电压在网侧电压产生波动时保持稳定,实现不停电、带负载调节[1-2]。由于存在零件加工与装配误差的不确定性,快速机构在能量的储存与释放过程中不可避免地会出现失效。储能过程是释能过程顺利完成的前提,为保障有载分接开关实现功能切换,避免产生上百千安的电弧放电或起火爆炸问题,要求快速机构在整个储能过程中运动可靠,即其运动误差在整个储能过程中应处于安全范围。因此,从保障特高压电网安全运行的角度出发,开展分接开关快速机构运动的可靠性分析至关重要。

根据所涉及的时间长度,将可靠性分析分为非时变可靠性与时变可靠性[3-5]2种类型。非时变可靠性又称点可靠性,指的是在某一个时间点上极限状态函数处于安全区域的概率,不受前面时刻运动失效的影响;而时变可靠性评估的是整个时间段上的可靠程度,受前面时刻失效的影响,即只要在这段时间上出现失效,则整个时间段上失效。上述分类同样适用于运动可靠性。考虑到有载分接开关重点关注的是快速机构在整个储能过程中的运动可靠性,但传统机构的运动可靠性大多集中于点可靠性,而时变运动可靠性分析能为工程设计阶段提供更为客观的服役性能评估,则仅考虑单个时刻点快速机构运行是否可靠已无法满足设计需求。因此,进行机构时变运动可靠性分析,针对有载分接开关快速机构运动机制确定运动失效的影响因素,探讨构件在整个运动区间内是否可靠,进而分析储能过程中构件实现预期运动轨迹的可靠度,具有重要的工程意义。

目前,针对有载分接开关可靠性的研究,大多集中于开关使用过程中的故障诊断与故障预测。Seo等[6]为避免噪声的耦合干扰,采用概率小波变换方法提取电弧信号,研制出一种电弧信号与振动数据相集成的状态监测系统,并对2种不同类型的有载分接开关实现了现场在线监测。王丰华等[7]根据有载分接开关切换时的振动信号特征,将贝叶斯估计与支持向量数据方法相结合,建立了机械故障诊断模型,并对某CM型有载分接开关在正常工作与发生故障时的状态进行有效识别。刘志远等[8]提出一种有载分接开关弹簧储能故障的识别方法,构建了神经网络响应面模型,并与有限元仿真结果进行比较,实现了不同激励力下故障特征的有效检测。李小双[9]对有载分接开关常见机械故障的类型和原因进行了分析,开发出多信号融合的机械故障诊断平台,利用万有引力搜索(GSA)优化算法对快速机构开展了故障诊断并具有较好的效果。金雷等[10]结合近年来真空有载分接开关发生的典型故障案例,分析了故障产生的原因,从多角度阐述了保证开关可靠运行的详细举措。毋庸置疑,运行阶段的故障诊断与预测对于有载分接开关可靠性保障具有重要意义,但遗憾的是,上述方法均不能应用于有载分接开关的时变运动可靠性分析。

本文结合分接开关快速机构的运动机制,研究了其运动失效影响因素,通过构建时变运动可靠性分析模型,提出了一种新的首次穿越率解析求解方法,并基于此求解方法得到了快速机构时变运动失效概率序列。与蒙特卡罗方法相比,该方法在计算效率方面具有明显的优势。最后,根据该方法进行了灵敏度分析,研究变量的分布参数对时变运动可靠性的影响程度,从而为分接开关快速机构可靠性分析的评估与参数优化设计提供支撑。

1 快速机构运动分析

快速机构组成构件示意图如图1所示[11],主要包括偏心凸轮、摆杆、齿轮1、拨钉、储能弹簧、拉杆、齿轮2和齿轮3。在储能过程中,偏心凸轮在电机输出转矩的驱动下,带动与其相配合的摆杆绕定轴摆动,摆杆在摆动过程中推动固连在齿轮1上方的拨钉运动,从而实现齿轮1绕中心轴顺时针转动,与齿轮1外啮合的齿轮2作反方向逆时针转动,此时,一端固接在齿轮2上的连杆被拉长,储能弹簧缓慢压缩并储存能量;当弹簧经过死点位置时,在储存能量的作用下会发生快速回弹,推动齿轮3转动,从而带动底层凸轮机构作90°转动,完成释能动作,此即释能过程。

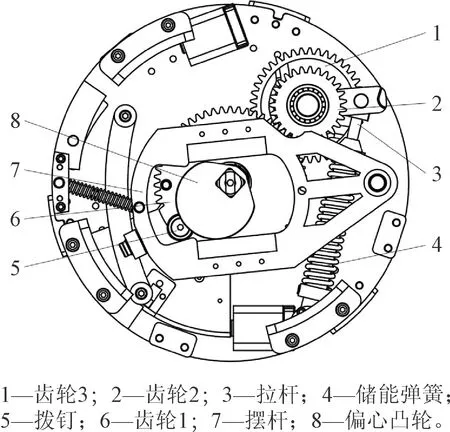
图1 快速机构组成构件示意图Fig.1 Components and motion analysis of quick mechanism

图2 储能弹簧形变量与力矩差值随时间的变化曲线Fig.2 Deformation and torque variations of energy storage spring with time

在实际工程中,由于不确定性因素的存在,快速机构不可避免地会存在运动误差[12-14]。图2给出了储能过程中,储能弹簧在理想状态下形变量的变化曲线,以及理想与实际状态下齿轮2所受弹簧力矩的差值。结合图1可知,理想状态下偏心凸轮的回转运动带动摆杆进行往复摆动,导致拉杆伸长,储能弹簧被压缩,满足规定的形变量条件,所受载荷沿轴心线方向。若拉杆的运动精度未达到预期要求,储能过程在规定时间段内出现运动偏差,当偏差超出一定范围后,一旦弹簧形变扭曲而引起贮存的能量不足或冗余,有载分接开关动作就会发生故障,严重时还会造成机构卡滞、拒动等,进而影响整个产品性能。因此,结合快速机构运动机制,对储能过程进行失效模式影响因素分析,研究其在整个运动时段上的可靠性具有十分重要的意义。

2 快速机构运动失效影响因素分析

如上所述,在机构运动可靠性分析中,一般存在非时变运动可靠性与时变运动可靠性两种情况。对于快速机构而言,由于要保障整个储能过程的可靠运动,因此开展时变运动可靠性分析更为重要,分析结果亦更为保守。进行时变运动可靠性分析的第一步是构建机构运动输入与输出间的关系,表示如下

ψ(θ,λ,X)=0

(1)

式中:ψ为独立运动方程;θ为机构输入角度;λ为机构输出角度;X为机构结构件参数。研究结构件参数即运动失效影响因素很有必要,因此,本文首先分析了快速机构的失效影响因素,为之后时变运动可靠性的分析提供数据基础。

2.1 关键构件磨损影响分析

结合图1中的快速机构二维示意图,可知在单次运动过程中,拨钉与偏心凸轮始终和摆杆保持接触状态,不可避免地会产生因机械运动而造成的磨损,因此接触碰撞所引起的构件磨损是快速机构运动失效的影响因素之一。本文所设计的拨钉与偏心凸轮的材料均为45钢,拨钉外径为30 mm,偏心凸轮偏心圆半径为44.5 mm。

如图3所示,从同批次样机中随机抽取3台,选取45 000次切换运动为试验步长开展切换试验。对试验采集到的拨钉外径数据进行多项式拟合,拟合后的曲线绘制于图4。

图3 快速机构样机切换试验Fig.3 Prototypical experiment of quick mechanism

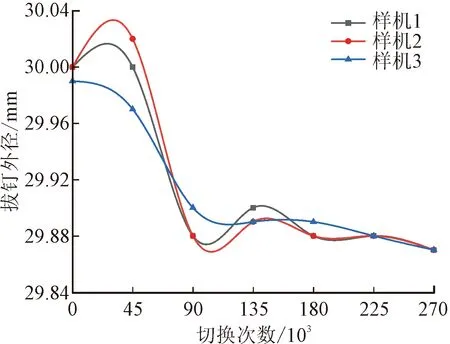
图4 快速机构拨钉外径拟合曲线Fig.4 Fitting curve of pin outer diameter of quick mechanism

对图4数据进行分析可知,在允许测量误差的情况下,当切换次数达到270 000次时,拨钉外径的最大磨损量仅为0.13 mm。由此可知,当快速机构在整个储能过程中单次运动时,快速机构的拨钉外径变化较小。由试验还可得到,偏心凸轮的磨损量在整个运动过程中变化缓慢。综上可知,由于关键构件的磨损对于快速机构单次运动可靠性影响很小,因此本文在进行时变运动可靠性建模时,可不考虑磨损的影响。

2.2 加工与装配误差影响分析

在快速机构加工装配过程中,针对同一批次零部件,构件尺寸可看作是服从正态分布的独立随机变量。下面,本文分析了此类不确定因素造成的随机误差对快速机构运动特性的影响。

采用机构等效替代方法,绘制快速机构运动学简图,如图5所示。利用快速机构储能过程的平面机构运动方程,基于矢量环方法构建运动误差函数,分别建立了封闭环路AEDCB与AHGB的机构矢量运动方程。

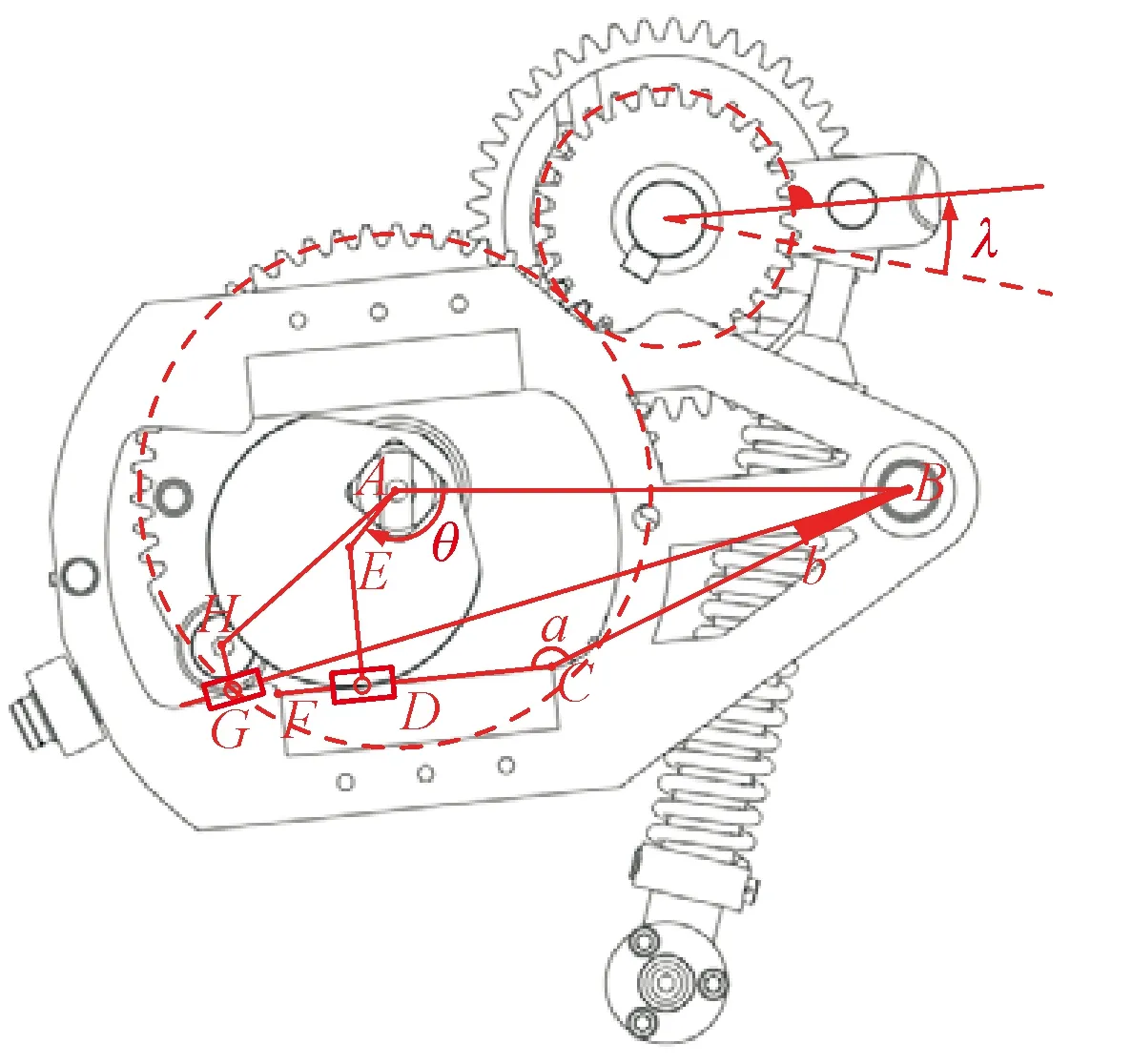
图5 快速机构运动学简图Fig.5 Kinematical diagram of quick mechanism

对于图5中的封闭环路AEDCB,得到机构水平方向与竖直方向的运动方程分别为

(2)

式中:l1、l2、l3、lCD和l4分别为杆AB、AE、ED、DC、CB的长度;a为∠BCD的角度;θ为杆AE的输入角度,即机构输入角度,则封闭环路AEDCB的输出角度λ1,即∠ABC,可表示为λ1(θ)。

将式(2)整理后,得到运动输入与输出之间的关系为

l2sin(a+θ+λ1)-l3+l4sina=l1sin(a+λ1)

(3)

同理,对于图5中的封闭环路AHGB,可得机构的水平与竖直方向的矢量运动方程分别为

(4)

式中:l5、l6和lBG分别为杆AH、HG和GB的长度;b为∠CBG的角度;λ2为杆AH的输出角度。将上式整理后,可得

-l1sin(λ1-b)+l5sin(λ1-b+λ2)+l6=0

(5)

至此,图1中偏心凸轮、摆杆、拨钉、齿轮1传动系统的运动输入与输出关系式构建完成。

图6 齿轮系统偏心参数Fig.6 Parameters of eccentricity for gear system

对于齿轮系统运动精度,主要考虑其因零部件加工和装配而造成的长周期误差,包括几何偏心和运动偏心[15-16]。如图6所示,主动齿轮(直径相对较大)与传动齿轮的回转中心分别为O′1、O2,假设主动齿轮运动时相对回转中心存在一当量偏心O1O′1,其偏心距为d,此时主从齿轮相啮合的点将不再在连心线上(见图7),从动齿轮实际转角与理论转角间会产生运动误差s,表达式可写为

(6)

式中:αn是渐开线圆柱齿轮压力角;γ是O1O′1与O1O2之间沿顺时针方向的夹角,在 [0,2π]内服从均匀分布;d是几何偏心和运动偏心的综合,服从瑞利分布,可由齿轮切向综合误差F′i估计如下

(7)

其中F′i可参考国家标准GB/T 10095.1—2008。

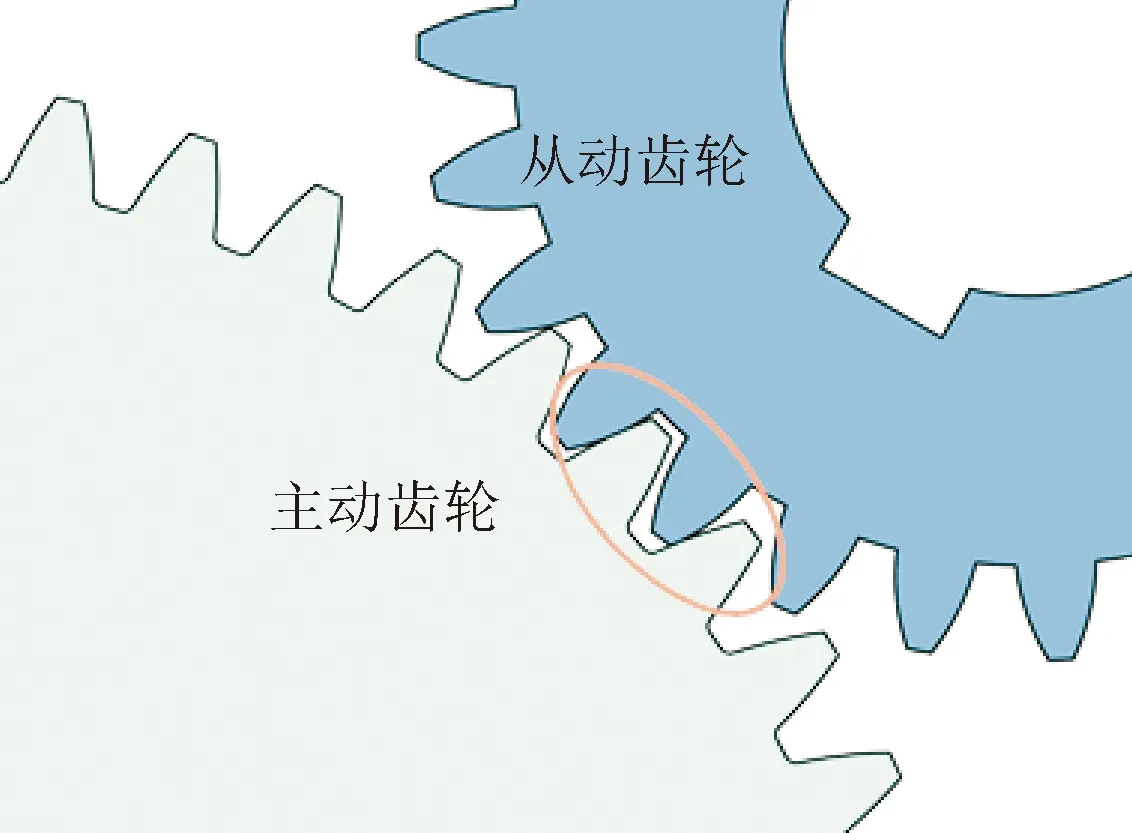
(b)偏心齿轮副

在实际工程应用中,为了便于描述,一般将运动误差s的线值转化为角度值。对于圆柱直齿轮,运动误差角度值φ与运动误差线值s间的关系可写为

(8)

式中:mn是从动齿轮法面模数;Z2是从动齿轮齿数。

考虑到γ在 [0,2π]内服从均匀分布,d服从瑞利分布,γ与d又相互独立,因此有

(9)

(10)

式中:f(·)表示概率密度函数;σ表示正态分布的标准差。进而可得到

(11)

令l7=dsinγ,l8=dcosγ,则有

(12)

将式(12)代入式(11)进行换元,根据概率变换得到,l7、l8满足l7～N(0,σ2)、l8～N(0,σ2),且l7与l8相互独立。

因此,从动齿轮运动角可写为

(13)

式中:λ20是杆AE与AB的初始夹角;Z1是主动齿轮齿数。

至此,快速机构在储能过程中的构件输入与输出间关系已全部得到。

2.3 快速机构失效模式影响因素确定

一般地,对于一个确定构型的输出机构,实际运动输出为λ(X,θ),理想运动输出为λ*(θ),则实际输出与理想输出之间的运动误差函数可写为

g(X,θ)=λ(X,θ)-λ*(θ)

(14)

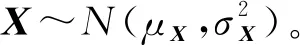
3 快速机构时变运动可靠性分析

对于时变可靠性,主要的分析方法包括蒙特卡罗法、极值分布法、代理模型法和首次穿越法等[17-20]。考虑到首次穿越法可实现时变可靠性的半解析求解,且能够在单次计算中给出时变失效概率序列,因此本文采用首次穿越率法开展分析。

假设不同时刻的穿越事件是相互独立的随机过程,则在 [t0,tf]时间段内从安全域到失效域的穿越次数服从泊松分布[21-22]。考虑到θ=ωt,其中角速度ω为机构输入角速度,则时变运动失效概率可表示为

(15)

式中:v(θ)为首次穿越率,指的是单位时间内发生穿越事件的概率;θ0和θf分别为机构运动的初始与终止时刻;pR(θ0)为输入为θ0时刻的非时变运动可靠性概率。

由式(15)可以看出,时变运动失效概率pF(θ0,θf)的求解依赖于首次穿越率v(θ)的计算。针对此问题,本文将采用一阶线性展开对运动误差极限状态函数进行估计,并利用高斯截断矩推导得到首次穿越率的解析解。

3.1 首次穿越率推导

首次穿越率是指单位时间内发生穿越事件(即穿越安全边界)的概率。图8给出了输入为θ时刻,运动误差极限状态函数g(X,θ)穿越上安全边界的示意图,其中“×”表示穿越安全边界,emax和emin分别为上安全边界和下安全边界的误差值。

图8 穿越事件示意图Fig.8 Representation of the outcrossing event

首次穿越率的表达式可写为

v(θ)=

v+(θ)+v-(θ)

(16)

式中:S是以emax和emin分别为上、下边界的安全区间;v+(θ)为穿越上边界的穿越率;v-(θ)为穿越下边界的穿越率。本节只进行上边界穿越率的求解,下边界穿越率可用相同的方法推导得到。

为了简化表达,假定式(16)中的g(X,θ)为变量ζ,g(X,θ+Δθ)为变量η,如图9所示,则根据积分变换可得到穿越上边界事件发生的概率为

Pr{g(X,θ)emax}=

(17)

式中:fg(X,θ),g(X,θ+Δθ)(ζ,η)为g(X,θ)和g(X,θ+Δθ)的联合概率密度函数。

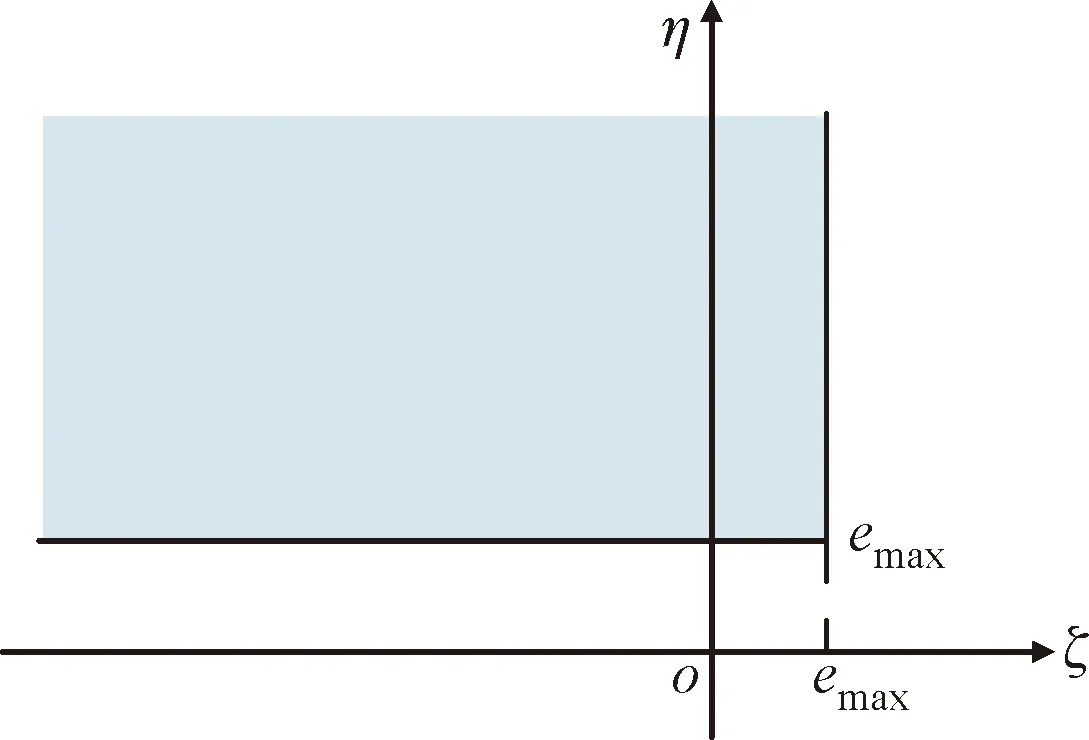
图9 穿越上边界事件发生概率积分变换示意图Fig.9 Schematic diagram of probability integral transformation of events outcrossing the upper region

(18)

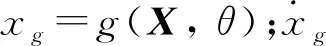
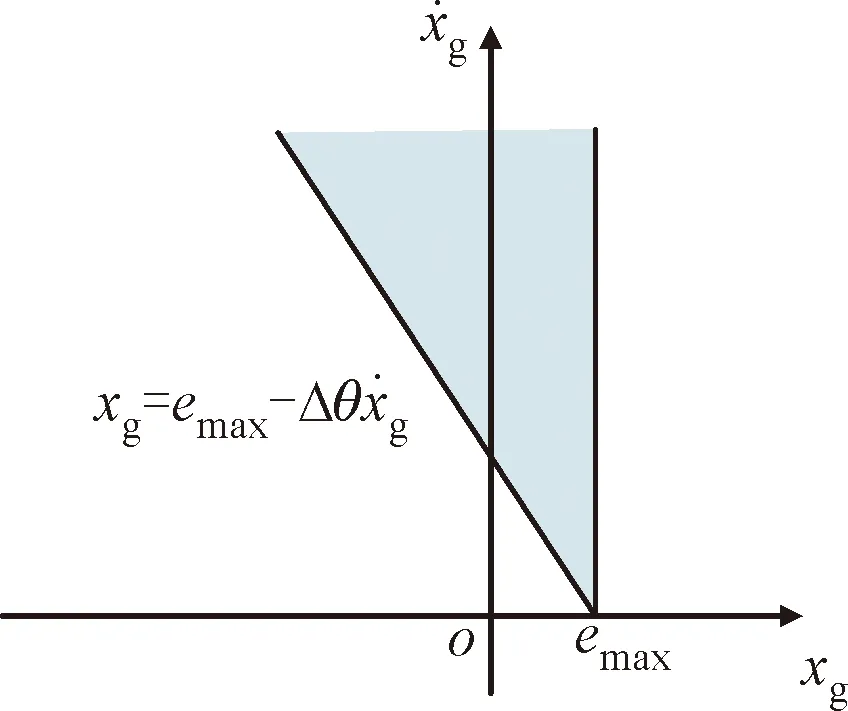
图10 坐标转化示意图Fig.10 The diagram after the coordinate transformation

根据上述坐标变换,式(17)中穿越事件发生的概率可以改写为

Pr{g(X,θ)emax}=

(19)

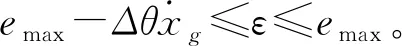
(20)

(21)

已知运动误差极限状态分布函数及其导数的联合分布是二维高斯分布,其均值与协方差分别为μ1和Σ1,可得μ1=02×1,Σ1可从多维高斯分布协方差矩阵Σ中得到,表示如下

(22)

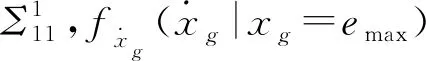
(23)

(24)

由此可得穿越上边界的穿越率,表示如下

(25)

将式(25)后半部分定义为

(26)

(27)

式中:erf(·)是高斯误差函数。

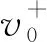
(28)

为了简化表达,令

(29)

(30)

(31)

将式(31)代入式(25),可以得到穿越上边界的穿越率

(32)

同理可得穿越下边界的穿越率

(33)

将式(32)和(33)一同代入式(16),就可得到首次穿越率v(θ)的解析表达式。

3.2 快速机构运动可靠性

在极限状态函数服从高斯分布的前提下,推导得到了首次穿越率的解析解,但实际上运动误差极限状态函数g(X,θ)并不能直接满足这个条件。由于快速机构中各构件的名义尺寸远远大于其制造公差或装配误差,即尺寸变量的标准差σl远小于其均值μl,故可将误差函数g(X,θ)在均值μl处进行一阶线性估计,将其从非高斯分布转化为高斯分布,以满足上述首次穿越率解析解的应用条件。

首先利用泰勒展开对g(X,θ)进行一阶估计,得到

(34)

为简化计算,令

li=μi+σiUi

(35)

式中:Ui～N(0,1)。

(36)

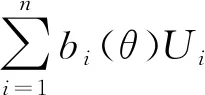
(37)

根据式(36)计算快速机构的随机误差,易得

b(θ) = [b1(θ),b2(θ),…,bn(θ)]

(38)

已知极限状态函数g(X,θ)满足式(14),由于机构的理想运动输出λ*(θ)只与输入的θ值有关,与构件的尺寸无关,则可通过

(39)

得到b(θ)的值。

(40)

(41)

式中:b′(θ)为b(θ)对θ的一阶导数。

(42)

(43)

对于输入为θ0时刻的非时变运动可靠性概率pR(θ0),可通过下式计算

pR(θ0)=Pr{emin≤g(X,θ0)≤emax}=

(44)

式中:Ф(·)是标准正态分布累积分布函数;μg(θ0)、σg(θ0)分别是运动误差极限状态函数在初始时刻的均值和标准差。

综上所述,可先通过式(32)和(33)对快速机构误差过程上、下穿越率进行求解,再由式(15)计算得到快速机构时变运动失效概率,具体过程总结如下。

步骤1确定运动误差极限状态函数g(X,θ),给定安全边界S。

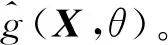
步骤3采用数值积分方法,由式(15)得到有载分接开关快速机构时变运动失效概率pF(θ0,θf)。

4 分析验证

根据图5中的封闭环路运动学模型,得到有载分接开关快速机构储能过程的输入角度θ,满足θ∈ [105°, 205°],输出角度为拉杆转动角度λ,理想输出角度为λ*。

根据工程经验,快速机构中各构件的名义尺寸及参数如表1所示。其中,标准差为0表示固定值。

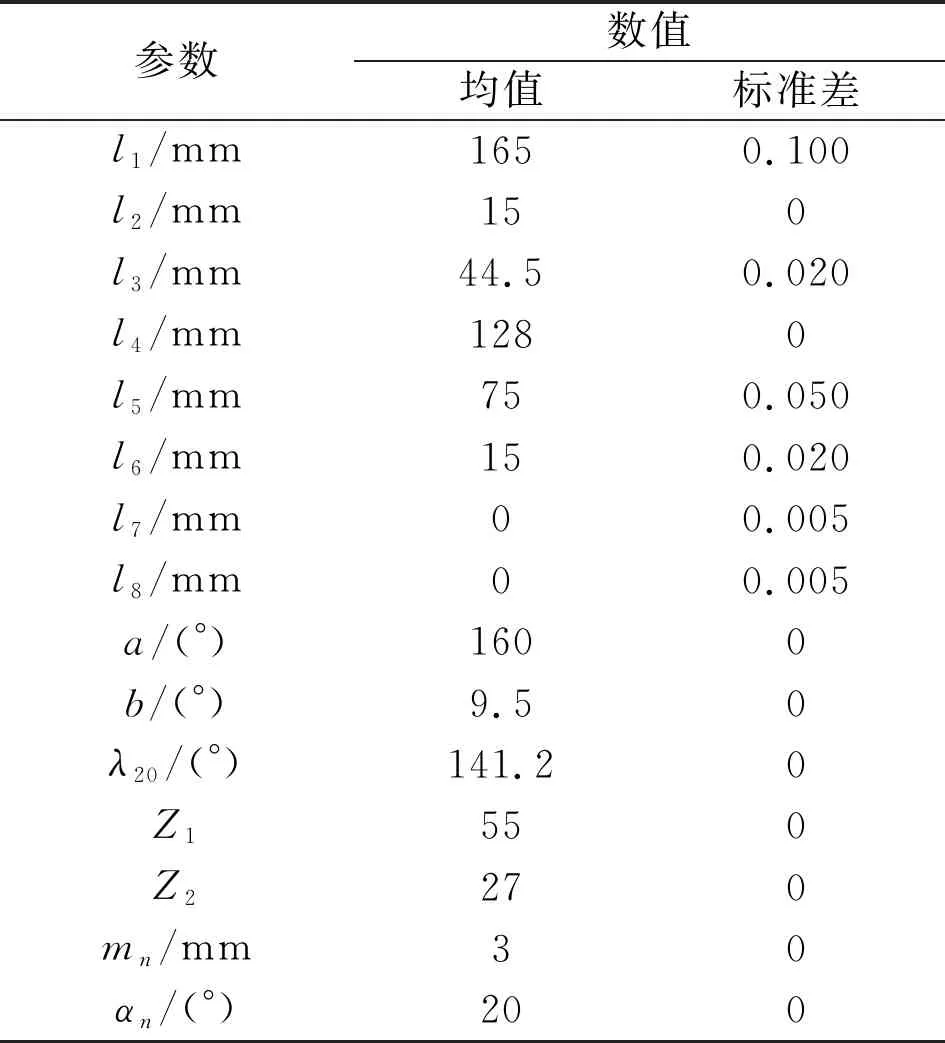
表1 快速机构基本参数

采用蒙特卡罗(MCS)算法进行验证,设定样本容量为105,时间区间内离散点的个数为200。同时结合文献 [3]中的首次穿越方法,计算各安全边界下的失效概率,如表2所示。其中,e为安全边界,pF、pF,MVFP和pF,MCS分别为本文方法、文献 [3]方法和蒙特卡罗方法所得到的时变运动失效概率。定义相对误差δ为

(45)

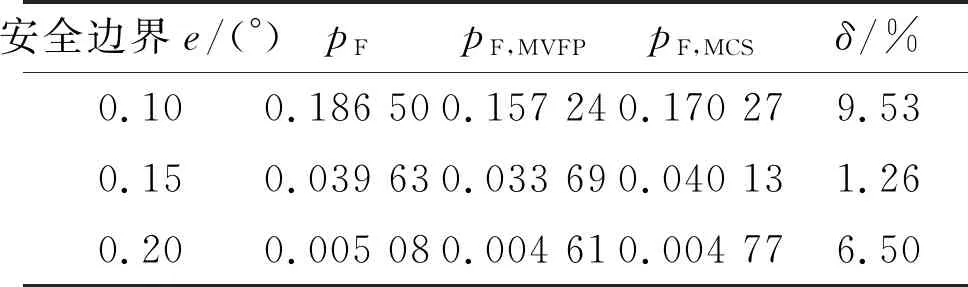
表2 3种方法得到的时变运动失效概率

针对安全边界为0.15°时的快速机构,分别采用本文方法和MCS方法计算时变运动失效概率,得到的结果如图11所示。由图可见,2种方法计算出的失效概率均随着输入角度θ的增大而增大。

图11 时变运动失效概率序列曲线Fig.11 Time-dependent kinematic failure probability sequence curves

在计算时间成本方面,本文方法针对每一个安全边界,Matlab2021b软件所需调用的函数次数为1,求解时变运动失效概率总调用函数次数为200×1=200。而蒙特卡罗方法总调用函数次数为200×105=2.0×107。2种方法所耗CPU(i7-6820HQ)时间的对比如表3所示,很明显,本文方法的时间成本远小于蒙特卡罗法,在计算效率上有着较大优势。由此可见,本文所提出的方法具有较高的求解精度与计算效率,这为机构时变运动可靠性的快速准确计算和灵敏度分析提供了理论支撑。

表3 2种方法计算时间对比

综上所述,在同一尺寸偏差下,随着安全边界范围的增大,时变运动失效概率递减。对于不同的安全边界条件,采用本文方法计算出的时变运动失效概率与蒙特卡罗法的迭代运算结果十分接近,相对误差小于10%,能够满足工程实际要求。

更改表1中部分机构尺寸参数,如表4所示,计算在此参数下快速机构的时变运动失效概率,结果列于表5。可以看到,此时的相对误差值同样符合工程需求,再一次验证了本文方法的有效性。

表4 快速机构基本参数

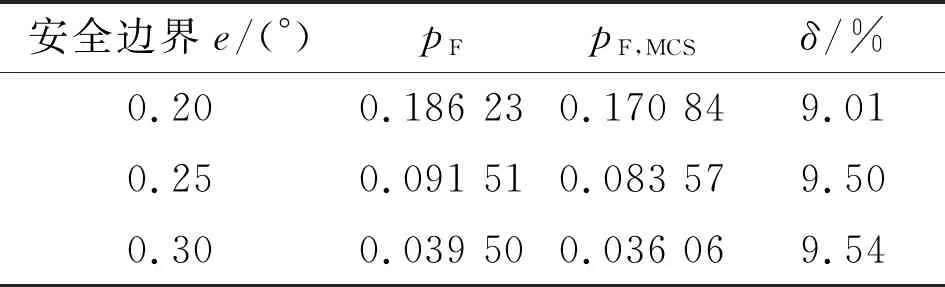
表5 2种方法得到的时变运动失效概率

根据以上结果,适用于整个时间区间上的时变可靠性模型已成功建立,这为时变可靠性问题中灵敏度的求解提供了前提。下面根据表1中机构的基本参数进行灵敏度分析。

由误差函数得到X=(l1,l3,l5,l6,l7,l8)为服从正态分布的六维随机变量,X的均值与标准差分别为μX=(μ1,μ3,μ5,μ6,μ7,μ8)和σX=(σ1,σ3,σ5,σ6,σ7,σ8)。根据式(15),可得到由于单位均值和标准差变化所引起的失效概率响应,即均值灵敏度和标准差灵敏度,分别表示为

(46)

(47)

给定安全边界e=0.15°,根据式(46)和(47),可计算出采用本文方法得到的灵敏度参数,如表6所示。

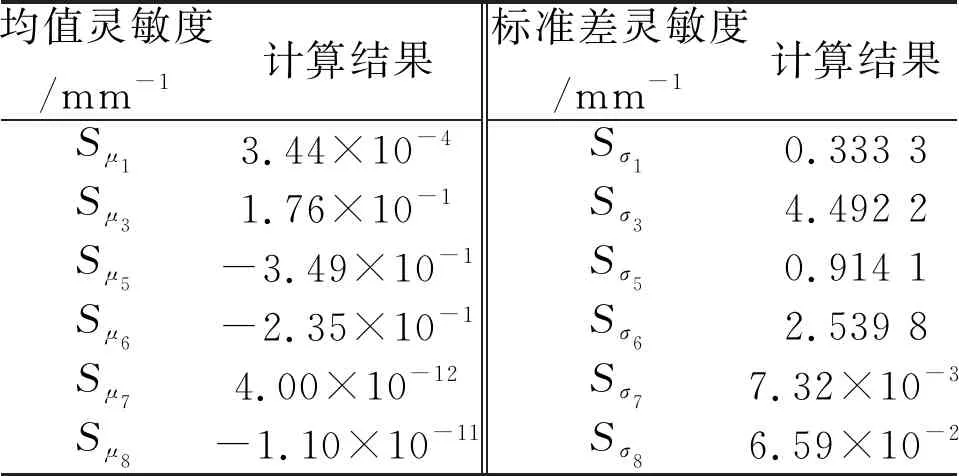
表6 快速机构可靠性灵敏度分析

由表6可知,均值灵敏度指标按绝对值由大到小排序为Sμ5、Sμ6、Sμ3、Sμ1、Sμ8、Sμ7,均值μ5对时变运动失效概率的影响最大,即μ5的微小波动便可对储能过程的可靠性产生较大影响,μ7和μ8的影响程度接近。均值灵敏度Sμ5、Sμ6和Sμ8为负值,表示时变运动失效概率随着均值的增大而减小;若灵敏度为正值,则变化趋势正好相反。标准差σ3对时变运动失效概率的影响最大,σ7的影响最小,且标准差灵敏度指标由大到小的排序为Sσ3、Sσ6、Sσ5、Sσ1、Sσ8、Sσ7。

根据以上分析,在所有的随机变量分布参数中,参数μ5和σ3对于时变运动失效概率有着重要影响。因此,在设计制造与加工装配过程中,应重点关注拨钉与齿轮1的装配精度以及偏心凸轮的偏心圆几何半径尺寸公差。

5 结 论

(1)分析了有载分接开关快速机构运动失效的影响因素,重点考虑了零部件在加工与装配过程中的随机误差,从而建立了时变运动可靠性分析模型,提出了一种以首次穿越法求解时变运动可靠性理论为基础,在均值处基于多维高斯分布随机过程的时变运动失效概率求解方法。该方法结合首次穿越方法中穿越上边界和下边界的穿越率概念,运用单变量正态函数的一阶原点矩,评估了机构随时间变化的运动可靠性。

(2)针对有载分接开关快速机构储能过程,快速准确地计算出了某一安全边界下的时变运动失效概率,实现了概率寿命预测。推导了快速机构时变运动可靠性灵敏度解析公式,计算结果表明:l7与l8的微小波动对于储能过程的可靠性影响较小,在机构设计优化时可忽略,而是需要重点考虑装配过程中安装在齿轮1上的拨钉的定位误差,以及偏心凸轮的偏心圆几何半径尺寸公差。

(3)在实际工程应用中,当构件尺寸公差较小时,本文方法精度高且计算成本低,可替代蒙特卡罗方法的多重迭代机制,用来指导关键部件的加工装配,以满足机械动作的可靠性与稳定性,避免因服役过程中的运动误差超出安全边界而造成的失效。