燃气轮机动力涡轮转子动力学相似试验模型的设计方法研究

2023-10-29黄朝晖袁奇余承智高进孔祥林

西安交通大学学报 2023年10期

黄朝晖,袁奇,余承智,高进,孔祥林

(1. 西安交通大学能源与动力工程学院,710049,西安; 2. 陕西省叶轮机械及动力装备工程实验室, 710049,西安; 3. 东方电气G50研发中心,610000,成都)

工业燃气轮机[1]广泛应用于天然气管道运输、发电、动力驱动、石油开采、取暖等关系民生[2]的重要行业。燃气轮机主要由压气机、燃烧室和涡轮3部分组成,其中涡轮是动力输出结构。较航空燃气轮机,工业燃气轮机应用在地面,它的体积较大,输出的功率较高,对于运行稳定性和工作寿命的要求也更高。

当今较为成功的工业燃气轮机主要有美国通用公司(GE)的LM2500、德国西门子(SIEMENS)的SGT-750等,工业燃气轮机的国产化[3]是我国产业升级的重要一环。工业燃气轮机大多采用双轴结构,即压缩机和高压涡轮同轴,动力涡轮与发电机或被驱动机械同轴。由于空间限制和二次空气系统的要求,动力涡轮转子一般设计为悬臂拉杆组合转子[4],多级涡轮轮盘完全悬于支持轴承外,这对于转子的强度[5]和稳定性提出了更高的要求。由于工业燃气轮机[6]造价高昂且尺寸大,难以直接开展动力学试验[7],因此以动力学相似原理构建等效缩比模型开展动力学研究十分有必要[8]。

达到动力学相似的条件[9]是缩比模型与原始模型[10]的固有频率、动力学响应特性和模态振型[11]等在工作转速范围内一致或有固定比例,对于燃气轮机动力涡轮转子[12],动力学相似[13]需要满足临界转速相似和模态振型一致。为实现动力学相似,等效缩比模型与原始模型需要在3个方面相似[14]:结构相似,保证缩比模型转子各个轴段质量分布和转动惯量空间分布一致;刚度相似,保证缩比模型转子使用材料抗弯刚度与原始模型转子抗弯刚度分布一致;边界条件相似,保证支承位置一致,若采用不同的轴承类型,刚度可以不一致。由于真实的动力涡轮转子往往含复杂结构[15],因此如果严格按照几何相似的原则建立缩比模型可能导致局部结构强度不足且难以加工,所以动力相似试验台的设计应该在符合动力学相似的基础上尽可能的简化几何结构。并且由于转子的临界转速与几何尺寸成反比,缩比系数的选取应该适当以避免动力学试验中临界转速过高。

文献 [13]基于相似理论提出了一种高速转子—支承结构系统动力学的缩尺相似设计方法,并通过建立转子的“超模型”进行有限元仿真计算验证了该方法的合理性。文献 [14]基于模型修正方法对航空燃气轮机涡轮转子缩比模型进行修正,得到预测精度较高的动力学相似模型。文献 [16]针对转子系统不平衡特征再现设计问题,提出一种基于动力学相似关系的模型再现方法,并利用有限元计算验证了方法的正确性。

目前,国内诸多类似研究的对象大多为航空燃气轮机转子,并且验证方式采用有限元仿真计算的方法。本文针对某公司研发的工业燃气轮机动力涡轮转子开展动力学特性研究,利用动力学相似原理构建缩比转子试验台,进行全转速范围试验和运行稳定性试验;同时,建立缩比转子的三维模型,对其进行模态和不平衡响应的三维有限元仿真计算;最后,对比试验和计算结果,验证了动力学相似试验转子模型的准确性和原始涡轮转子模型设计的合理性,为类似转子系统的动力学特性研究和设计提供了可靠的参考依据。

1 研究方法及模型

1.1 研究总体思路

本文通过建立某型工业燃气轮机动力涡轮动力相似等效缩比转子模型进行动力学特性研究,动力涡轮工作转速为3 075～6 457 r·min-1,根据原转子动力学特性,动力相似试验转子模型需要保证第一阶临界转速和第一阶振型相似。

研究总体思路如图1所示,主要分3步:构建动力涡轮原始模型、添加边界条件、进行模态仿真,得到的计算结果与企业提供的计算结果对比,以验证模态分析的准确性;确定动力相似关系,根据所给动力涡轮参数得到动力相似等效缩比转子模型参数以及边界条件,并同时建立动力相似试验转子模型和相应试验台;分别进行动力学特性有限元仿真计算和转子动力学特性试验,并将所得仿真结果和试验结果进行对比,并验证是否满足第一阶临界转速和第一阶振型相似,如果仿真结果和试验结果不一致或不满足相似要求,则需要调整动力相似试验转子模型参数,重新进行设计研究。

1.2 数值研究方法及理论

1.2.1 动力相似等效缩比模型的建立

本文主要针对临界转速和振型构建相似关系[17],建立动力涡轮转子的振动微分方程

(1)

式中:I为截面惯性矩;E为弹性模量;l为轴向长度;γ为合成挠度;t为时间;ω为系统的固有频率;Jρ为圆盘的极转动惯量;m为转子的质量;p为转子中不平衡力的强度。

沿转子轴中心线的倾角α和法向应力σ分别为

(2)

式中:W为抗弯截面系数;M为弯矩。

由式(1)、(2)推导出相似准则的π系数群为

(3)

式(3)中各个变量的因次之间关系为

(4)

将式(4)代入式(3),得到简化的π系数群

(5)

为了实现缩比模型和原始模型的动力学相似[18],则必须保证它们相应的π值相等。由于本文主要以转子的一阶临界转速和一阶振型为动力相似的标准,根据式(5)可以得到动力相似等效缩比模型和原始模型质量m、刚度k和临界转速ωn的等效缩比关系式[19]为

(6)

式中:Kd为直径缩比系数;Kl为轴向长度缩比系数;KE为弹性模量缩比系数;Kρ为密度缩比系数。

1.2.2 动力相似等效缩比模型的评估

建立的动力相似试验转子模型[20]需要进行评估以验证建模的准确性,针对临界转速的相似程度[21]使用相对误差Es来进行评估

(7)

式中:ωm为动力相似试验转子模型临界转速,r·min-1;Kω为临界转速缩比系数;ωp为原始模型临界转速,r·min-1。

本文通过建立动力相似试验转子模型[21]来检验原始涡轮转子模型设计的合理性,所以使用API 612高速动平衡[22-24]标准来验证转子运行的安全性。

API 612悬臂端许用不平衡量为

(8)

式中:m1为悬臂端质量,g;n为转速,r·min-1。

API 612允许转子悬臂端轴承座附近最大不平衡响应峰-峰值振幅为

(9)

式中:N为最大运行转速,r·min-1。

本文以转子各阶固有频率的对数衰减率δ是否大于0.2为运行稳定性标准[25]。Q因子是无量纲量,Q因子大表示振动模态的阻尼小,共振峰尖锐。Q因子与模态阻尼比ζ和对数衰减率δ的关系为

(10)

Qδ≈π

(11)

计算模态阻尼比ζ最常用的方法为半功率带宽法。半功率带宽法是在自振频谱图上对每一阶自振频率采用半功率点带宽求取阻尼参数的方法,其理论计算式为

(12)

式中:f0为系统固有频率;f1、f2为半功率点频率。

1.2.3 动力学仿真计算网格模型和边界条件

本文选取动力相似试验转子的材料为40Cr,密度比原涡轮转子使用的IN718略小,密度缩比系数Kρ=0.94,弹性模量缩比系数KE=1,轴向长度缩比系数Kl=0.25,直径缩比系数Kd=0.15,其余各物理量缩比关系如表1所示。

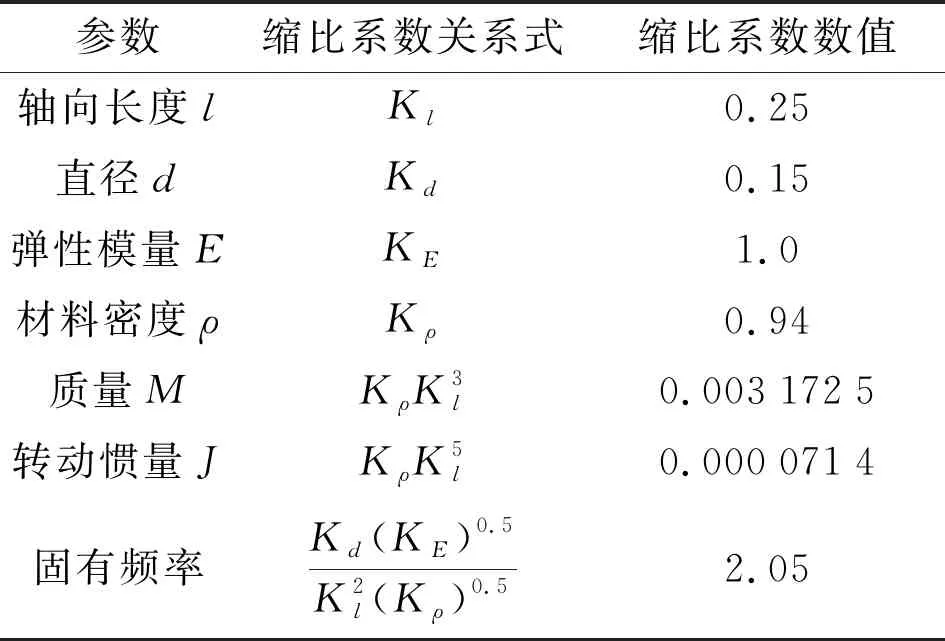
表1 动力相似试验转子模型和原始涡轮转子模型各物理量缩比关系

根据所得缩比系数和原始涡轮的参数可以求得动力相似试验转子模型的具体参数,其中动力相似试验转子模型与原始模型的跨外和跨内质量比均约为2.1,悬臂端静挠度均为54 μm,表2为原始模型和动力相似试验转子模型相关参数对比。

表2 动力相似缩比转子模型和原始涡轮转子模型相关参数对比

原始动力涡轮转子结构示意图如图2所示,边界条件为进气侧轴承座刚度5×108N/m,排气侧轴承座刚度为5×107N/m。其轴承为可倾瓦轴承,而本试验中为圆轴承,所以本文的试验和仿真计算施加的边界条件为两轴承座刚度均为8×106N/m。

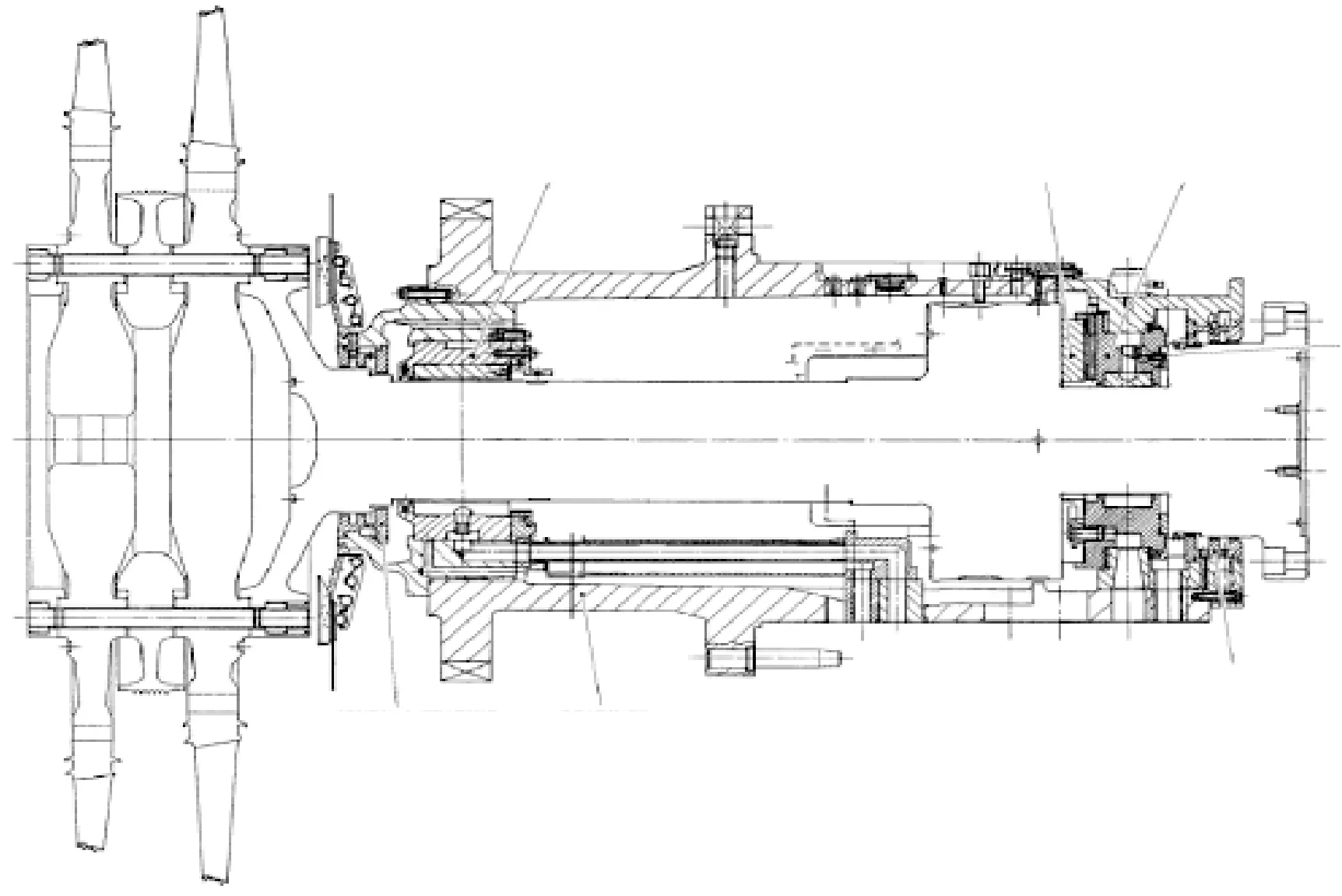
图2 原始动力涡轮转子结构Fig.2 Original power turbine rotor structure

使用三维有限元仿真软件ANSYS按照计算所得的几何参数建立动力相似试验转子模型,并使用ICEM对所得转子模型进行网格划分,网格类型为六面体网格,网格数为54 623,节点数为21 457,三角形标志处为轴承支承位置,如图3所示。

(a)几何模型

(b)三维有限元网格模型

1.2.4 动力相似试验研究方法

根据动力相似准则建立动力相似试验台,试验台包括动力相似试验转子系统、测量系统和轴承润滑油路系统。动力相似试验转子系统包括跨外悬臂轮盘、跨内轮盘、轴承座和直流驱动电机;测量系统包括位移测量、转速测量和温度测量;油路循环包括油泵、输油管和油箱。动力相似试验转子模化试验台如图4所示。

图4 动力相似试验转子模化试验台Fig.4 Dynamic similarity test rotor modeling test bench

动力相似试验转子模化试验台的测量系统共包括6个位移传感器、一个转速传感器和两个温度传感器。位移传感器和转速传感器均使用中航科技公司生产的ZA-21系列电涡流传感器,适配直径3 mm探头,最大量程500 μm,标准灵敏度20.000 V/mm,使用±15 V供电电源;温度传感器使用PT100型热电阻温度传感器,用于测量靠近悬臂端的轴承轴瓦温度。信号采集器使用FOCUS Ⅱ高精度测试系统,频率精度在0.01%以内,信号处理使用RT Pro动态信号分析处理软件。动力系统使用额定功率750 W直流电机,最大转速为7 000 r·min-1,大于原始涡轮转子最大工作转速6 457 r·min-1。试验转子采用内直径30 mm、外直径100 mm的轮盘进行配重,每个轮盘上均有等角度分布的12个直径5 mm的平衡孔用于进行转子高速动平衡。通过计算,转子悬臂端跨外部分安装70 mm厚轮盘、跨内部分安装2个10 mm厚轮盘和1个20 mm厚轮盘,此时悬臂端静挠度为54 μm,试验台传感器测点安装位置和轮盘质量分布如图5所示。

图5 动力相似转子试验台布置示意图Fig.5 Layout diagram of dynamic similar test bench

试验主要包括升速试验和稳定运行试验。升速试验的目的是通过对动力相似试验转子施加不同动平衡标准下的不平衡量来测量全转速范围内转子振动响应峰-峰值;稳定运行试验则是在施加了一定的不平衡量下,检验转子能否在临界转速附近长期稳定运行。

2 结果与讨论

2.1 原始动力涡轮转子的动力学特性分析

首先对原始动力涡轮转子进行有限元模态仿真计算并将所得结果与企业所给报告结果对比,确定原始模型的临界转速。使用UG软件建立原始动力涡轮转子模型,使用ICEM软件对模型进行网格划分,网格类型为六面体,网格数为188万,节点数为140万,图6中红色三角处为轴承约束的位置。

使用ANSYS有限元仿真软件对原始涡轮转子进行模态仿真分析,表3为模态仿真计算结果与企业所给计算结果的对比,可知仿真计算结果相对误差均在4.9%以内,说明临界转速计算结果可信。

(a)几何模型

(b)网格模型

图7为有限元仿真计算所得各阶临界转速的模态振型,其中第一阶振型为外伸端刚体摆振、第二阶振型为右端摆振、第三阶振型为跨内一阶弯曲。根据动力涡轮工作转速范围和企业要求,动力相似的参考标准为第一阶临界转速是否成比例和第一阶振型是否为外伸端刚体摆振。由1.2.3节可知固有频率的缩比系数为2.05,故动力相似试验转子的第一阶临界转速应在3 200 r·min-1左右。

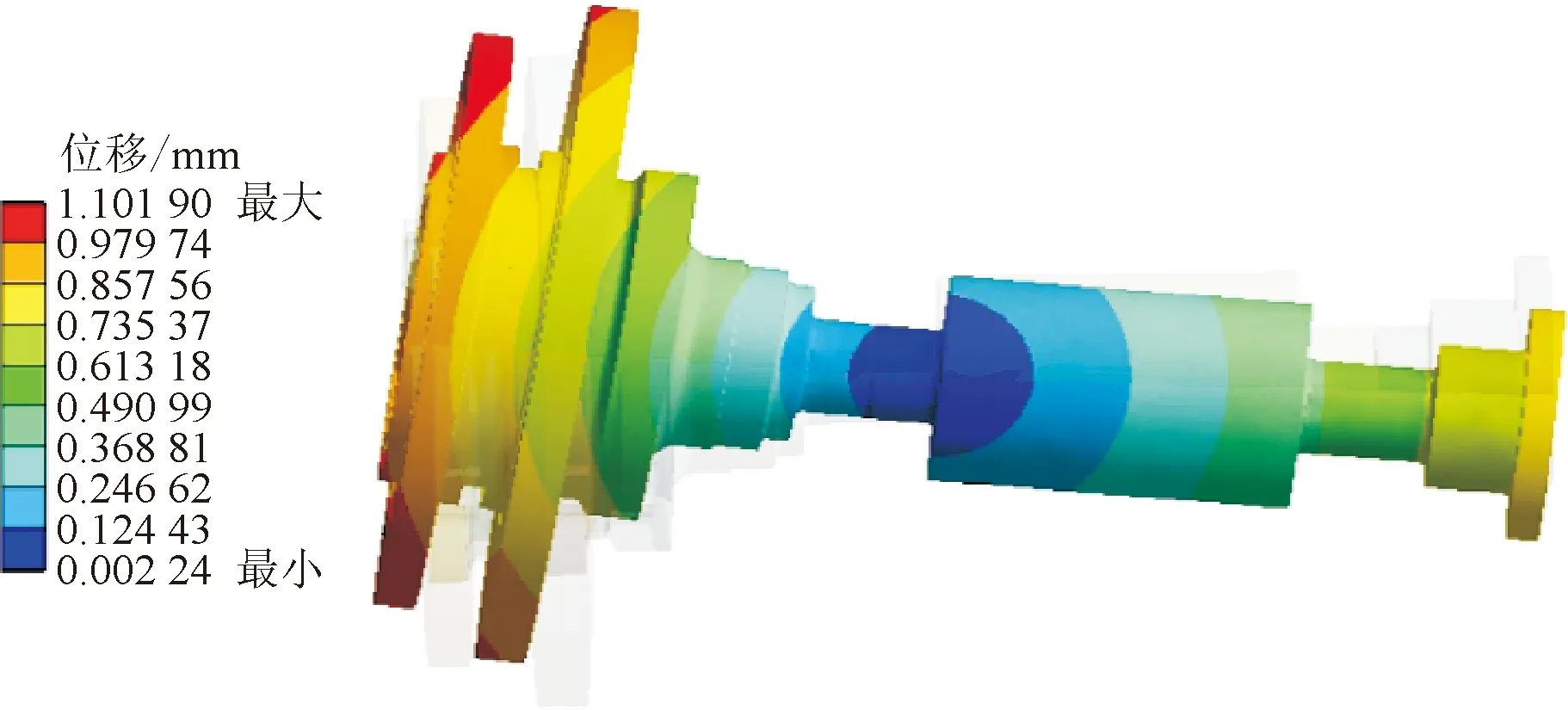
(a)第一阶临界转速为1 641 r·min-1(外伸端摆振)

(b)第二阶临界转速为3 665 r·min-1(右端摆振)

(c)第三阶临界转速为13 017 r·min-1(跨内一阶弯曲)

2.2 动力相似等效缩比转子模型动力学特性计算

使用ANSYS有限元仿真软件对动力相似试验转子模型进行模态仿真计算,施加边界条件:前、后轴承座刚度均为8×106N·m。模态分析结果如图8所示,可知:第一阶临界转速为3 120 r·min-1,振型为外伸端摆振;第二阶临界转速20 574 r·min-1,振型为右端摆振;第三阶临界转速33 240 r·min-1,振型为跨内第一阶弯曲。

(a)第一阶临界转速为3 120 r·min-1(外伸端摆振)

(b)第二阶临界转速为20 574 r·min-1(右端摆振)

(c)第三阶临界转速为30 120 r·min-1(跨内一阶弯曲)

使用ANSYS Workbench软件的Harmonic response analysis模块对动力相似试验转子进行不平衡响应分析。由于转子的第一阶弯曲振型为跨内第一阶弯曲,对应的临界转速远大于最大工作转速6 457 r·min-1,所以该转子属于刚性转子,在加载不平衡量时采用刚性转子的标准。

使用API 612动平衡标准,由式(8)计算得转子需施加的标准不平衡量为5.36 g·mm,边界条件不变,添加不平衡量示意图如图9所示,不平衡响应结果如图10所示。

图9 动力相似模化转子试验台添加不平衡量示意图Fig.9 Schematic diagram of adding unbalance on dynamic similarity model rotor test bed

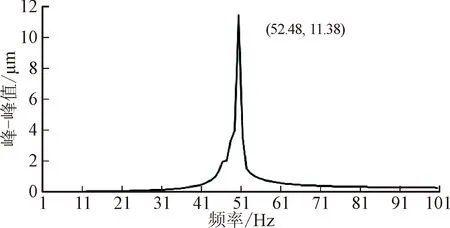
(a)动力相似试验转子振幅频率响应图

(b)动力相似试验转子相位频率响应图

由图10可知,动力相似试验转子在工作转速内、动平衡标准为API 612时外伸端轴承座附近最大响应峰-峰值为11 μm。根据式(9)可知,最大转速为6 457 r·min-1时,API 612标准允许最大峰-峰值为33 μm,说明动力相似试验转子在工作转速区间内符合安全标准。

2.3 动力相似等效缩比转子模型动力学特性试验

使用搭建的动力相似试验台开展动力学特性试验,分别开展升速试验和稳定运行试验。试验转子共设置3个测点,测点1位于跨内段近电机端轴承处、测点2位于跨内段近外伸端轴承处、测点3位于外伸段处,每个测点分别在水平方向与垂直方向布置电涡流位移传感器,以实现试验转子响应幅值的测量。为了减少试验开始时油温不稳定导致的转子振幅变化,本节试验中电机端轴承和外伸端轴承均采用油泵供油,同时在每组试验进行前完成数分钟的低速盘车以对试验台进行预热。

升速试验使用的动平衡标准有G0.4、G1.0、G2.5和API 612,不同动平衡标准下需要施加的不平衡量如表4所示。在进行试验前首先需要进行高速动平衡,确保转子的剩余不平衡量尽可能地小。经过计算,试验转子经过高速动平衡后的剩余不平衡量为4.88 g·mm,优于动平衡标准G0.4。施加不平衡量具体数值如表5所示。

表4 动力相似试验转子不同高速动平衡标准下的许用不平衡量

表5 动力相似试验转子各试验组许用不平衡量和实际不平衡量对比

升速试验过程中环境温度约为20℃,进油温度为17℃,进油压力0.15 MPa。试验中转子转速最高升至7 000 r·min-1,各测点升速过程中转速-响应幅值关系线如图11所示。当动力相似试验转子采用G2.5的动平衡标准时,转子在升速过程中最大响应峰-峰值位于测点1垂直方向,大小为70 μm。按照工业燃气轮机的运行标准,转子工作转速内的最大响应峰-峰值小于128 μm时,视为运转情况良好,因此动力相似试验转子符合安全规定。同时,当动力相似试验转子采用API 612动平衡标准时,悬臂端最大响应峰-峰值为12 μm,小于API 612标准规定的最大峰-峰值为33 μm,说明试验转子的悬臂端设计合理,符合安全标准。

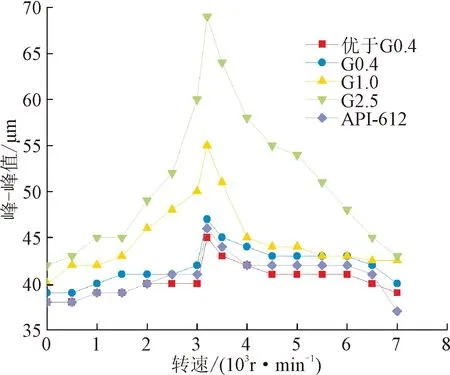
(a)测点1垂直方向

(b)测点1水平方向

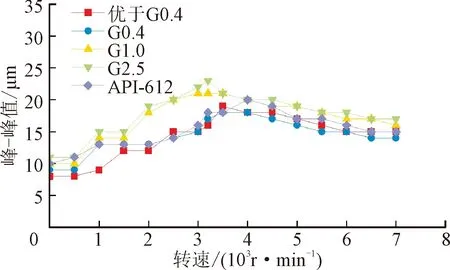
(c)测点2垂直方向

(d) 测点3水平方向

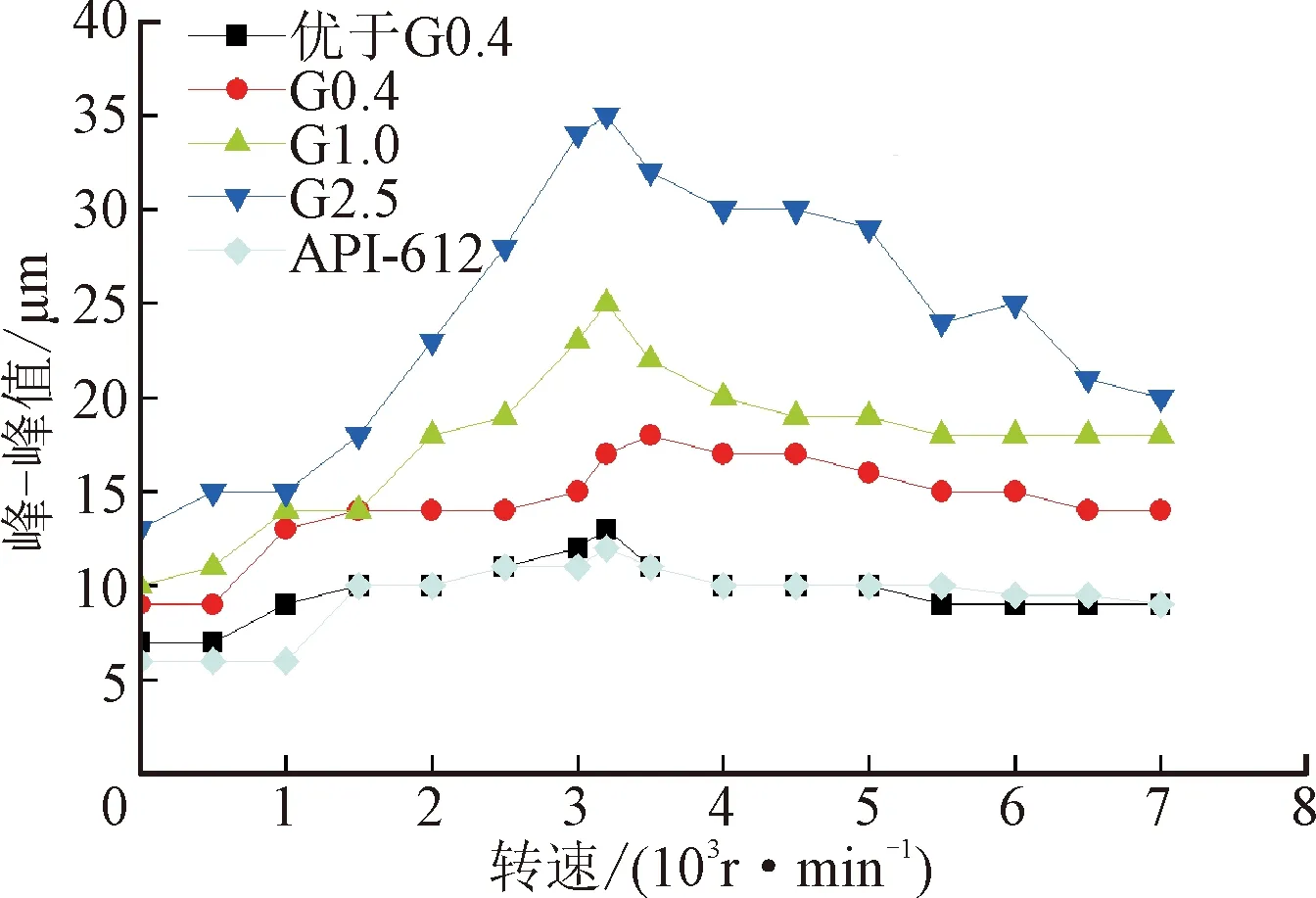
(e)测点3垂直方向

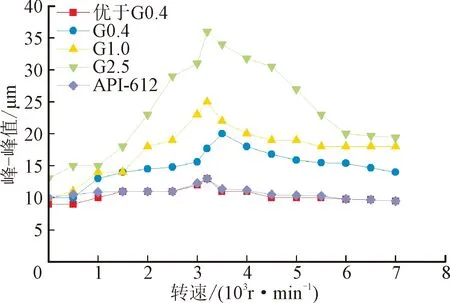
(f)测点3水平方向

各个动平衡标准下升速过程中的转子临界转速如表6所示,可知转子的一阶临界转速分布在3 100～3 300 r·min-1区间内,取API 612动平衡标准下的一阶临界转速3 266 r·min-1作为试验测得一阶临界转速值。动力相似试验转子的最大响应峰-峰值均位于测点1处,悬臂端最大响应峰-峰值为36 μm,完全符合安全稳定运行标准。

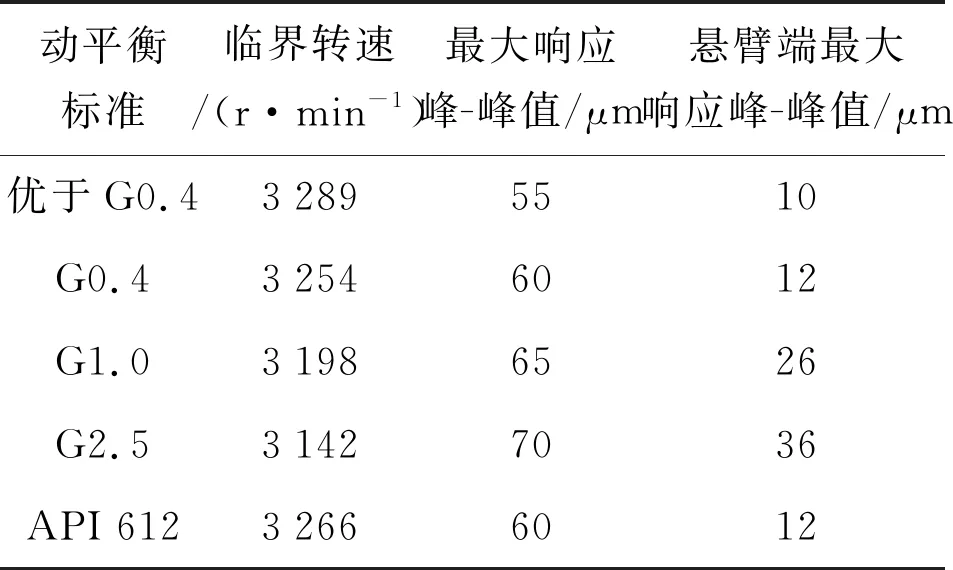
表6 不同动平衡标准下测得的动力相似试验转子第一阶临界转速

由于原始涡轮转子的工作转速为3 075～6 457 r·min-1,而动力相似试验转子的第一阶临界转速为3 266 r·min-1,位于工作转速范围内,这意味着转子在运行过程中需要在接近该临界转速长时间平稳运行。因此,将施加动平衡标准G2.5不平衡量的试验转子转速维持在3 266 r·min-1附近约1 h,转子可以在第一阶临界转速附近长期稳定运行,试验过程中响应峰-峰值曲线未出现大幅波动,如图12所示。

(a)转子运行转速随时间变化

2.4 动力相似等效缩比转子模型的验证

对动力相似等效缩比转子模型的有效性进行验证,动力相似试验转子模型的第一阶临界转速的有限元仿真计算结果和试验结果相对误差小于4.5%,说明所得临界转速结果可靠。如表7所示,动力相似试验转子的一阶临界转速与原始涡轮转子模型的一阶临界转速比值大约为2.05,说明本文所建动力相似试验转子模型可有效预测原始涡轮转子模型的临界转速。

对原始涡轮转子模型和动力相似试验转子模型进行运行稳定性评估,由表8可知,两转子的固有频率对数衰减率均大于0.2,说明原始动力涡轮转子模型和动力相似试验转子模型均可满足稳定运行的要求,转子设计安全可靠。

表8 原始动力涡轮转子模型和动力相似试验转子的稳定性评估

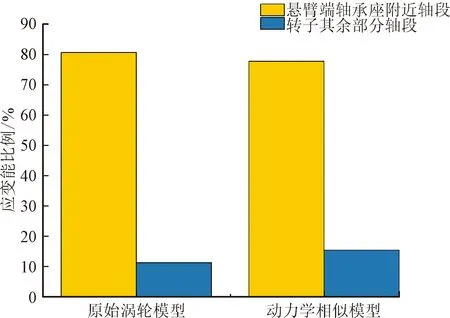
图13 原始模型和动力相似试验转子模型一阶临界转速应变能分布Fig.13 Distribution of strain energy at the first critical speed of the original model and the dynamic similarity model

图13为原始动力涡轮转子模型和动力相似试验转子模型在第一阶临界转速时应变能的分布,由图13可知,原始动力涡轮转子第一阶临界转速时的应变能主要分布在悬臂端轴承座附近。其中,原始动力涡轮转子模型在悬臂端轴承座附近的应变能占总应变能的比例为80.5%,动力相似试验转子模型为77.6%,而转子部分的应变能占比分别为11.2%和15.3%。说明动力相似试验转子模型可以较好地预测原始涡轮转子模型的应变能分布,所产生的误差应为结构简化所致。