基于小波能量熵和邻域粗糙集的电磁阀故障诊断研究
2023-10-28詹湘琳刘洪越
詹湘琳,刘洪越,荆 涛
(中国民航大学 电子信息与自动化学院,天津 300300)
0 引言
液体电磁阀是航空变量柱塞泵系统的关键组件,其作用是以通电和断电的方法改变航空变量柱塞泵斜盘倾角的大小[1],从而改变了泵缸体中柱塞的行程尺寸,导致泵的输出流量发生变化。然而液体电磁阀作为系统的关键执行部件受震动、颠簸和潮湿等工作环境影响,很容易产生弹簧刚度下降和阀芯油污阻滞等故障,使得航空变量柱塞泵系统输出不稳定,严重时导致柱塞泵发生泄漏或供油量不足[2],影响飞机飞行安全。所以为了提高系统的安全和可靠性,需要对液体电磁阀故障的及时检测和故障诊断。
目前,国内外学者对电磁阀的故障诊断进行了一定的研究。液体电磁阀故障诊断方法主要分为两类:模型驱动故障诊断和数据驱动故障诊断。模型驱动的故障诊断基于模型参数和故障特征之间的密切关系。Bayat[3]等人通过研究液压阀中的比例电磁铁,使用有限元模拟对电磁阀进行了分析,给出了所有电枢位置和不同电流下的电磁力和磁链的特性;武文韬[4]通过对电磁阀的原理进行分析,并建立电磁阀的数学方程,对已有的工况进行仿真,获得曲线并采用卷积神经网络进行故障诊断;唐勇等人[5]诊断了基于动态流量软测量的液压故障系统技术,探讨了泵压力脉动对设备的影响。但由于液压阀模型参数较多,想要模拟非理想化的电磁阀工作模型并非易事。
苏东海等人[6]利用单片机控制系统,通过步进电机和螺旋副的转动,将电机的旋转转化为线性位移,带动阀芯位移,控制变量活塞的运动,从而改变柱塞泵的输出流量;郝圣桥等人[7]通过测试液压电磁阀进出口压力,采集振动信号和压力信号对电磁阀进行故障诊断,但操作复杂,工程上难以实现,且通过干涉手段(如流量或压力)检测电磁阀可能会损坏原有的液压系统;张东来[8],马鑫等人对电磁阀的缓变失效进行了研究,利用电磁阀随开关次数增加而老化过程,提出基于电流特性的方法进行缓变失效研究,但其并未对电磁阀具体故障类型进行诊断。因此本文利用采集电磁阀驱动端电流来进行故障诊断的方法。然而小波变换在时频化局部分析上有一定的局限性,同时其处理非线性、非平稳信号时存在的缺陷。小波包分解可以有效避免小波变化的缺陷,但是在进行电磁阀故障诊断时,总会有些冗余的分量造成结果的不准确或运算的繁琐,减弱算法的推广性能。
为解决上述问题,引入属性约简算法删除冗余属性,在不丢失故障信息的情况下,选取敏感属性作为约简算法的输入。首先,对于提取的电磁阀故障电流曲线,使用小波包分解提取不同故障的频段能量值。然后,使用一种基于可变精度模糊邻域粗糙集的属性约简新方法[9],克服了原始组合的经典缺陷,可以有效地选择敏感属性,对于约简之后的属性值,用C4.5算法构建决策树[10],决策树使用自顶向下的回归方法进行划分。用特征量在内部节点决策树中进行测试,并根据特征值确定节点的分支[11],使诊断结果在节点表中显示。故障诊断流程如图1所示。

图1 电磁阀故障诊断模型
1 电磁阀故障机理分析
1.1 电磁阀结构与故障形式
电磁阀主要由阀体、阀芯、衔铁和线圈组成,基本结构如图2所示。当电磁阀断电或通电时,利用电磁力带动阀芯运动,控制阀门的通断。
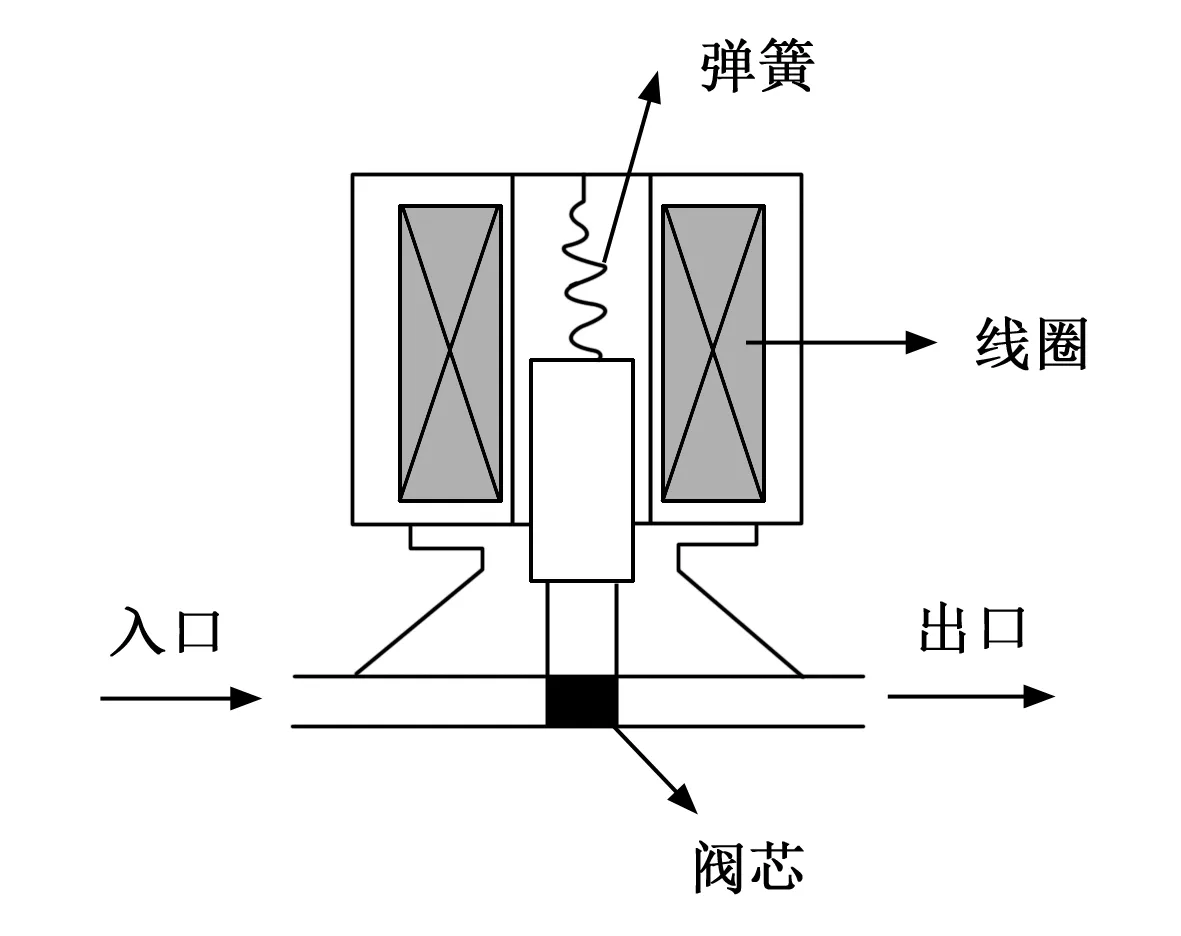
图2 液体电磁阀基本结构
由于线圈的电磁特性和阀芯的机械特性,电磁阀整个工作过程分为:吸合触动阶段,吸合运动阶段,通电保持阶段,释放触动阶段和释放运动阶段[8]。
在电磁阀的使用中,驱动电压异常、线圈绝缘材料的劣化、液体中的大粒子杂质、回位弹簧的断裂等是常见的故障类型,与其对应的引发原因如表1所示。
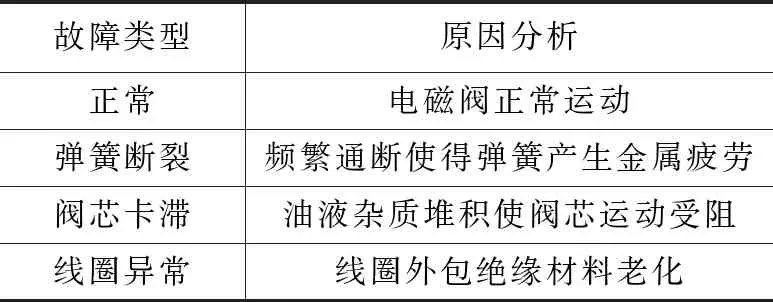
表1 故障类型与引发原因
因此,通过判断电磁阀的故障类型,可判断引发电磁阀不同故障的原因,实现对电磁阀的故障诊断研究。
1.2 电磁阀电特性分析
本文对电磁阀的通电和断电过程进行了仿真实验,并对结果进行了分析。依据电磁阀工作原理,将其整个工作过程简化为 3个数学方程:电路方程、磁路方程和运动方程。
开关电磁阀核心部件是电磁铁,通过分析电磁铁的实际工作条件[12],建立等效电路,如图3所示。

图3 电磁阀的等效电路图
得电磁铁的电路方程:
(1)
式中,U为励磁电压;R为线圈回路总电阻;i为等效回路中的电流;L为线圈电感。
电磁部分等效磁路方程为:
(2)
式中,μ0为真空磁导率;D为阀芯直径;N为线圈匝数;x为阀芯位移;lv为阀芯衔铁部分长度;l0为工作气隙最大宽度;r为工作气隙最大宽度。
在阀芯运动过程中,产生摩擦的主要有两个来源:阀芯与阀体之间的摩擦和阀芯与油液之间的摩擦。当电磁阀通电时,线圈产生的电磁力会克服弹簧的弹性力和阀芯的摩擦力,从而推动推杆通过电枢使阀芯运动。以阀芯为研究对象,当开关电磁阀通电时,根据牛顿定律,可推导阀芯的运动平衡方程为:
(3)
式中,k为弹簧系数;Cf为粘滞性阻尼系数;Cv为摩擦力系数;m为阀芯块质量;Fe为线圈通电时产生的电磁力,可以表示为:
(4)
根据上述电磁阀工作原理及数学模型,利用AMESim基本元件设计库(HCD)建立电磁阀的动态模型,如图4所示。
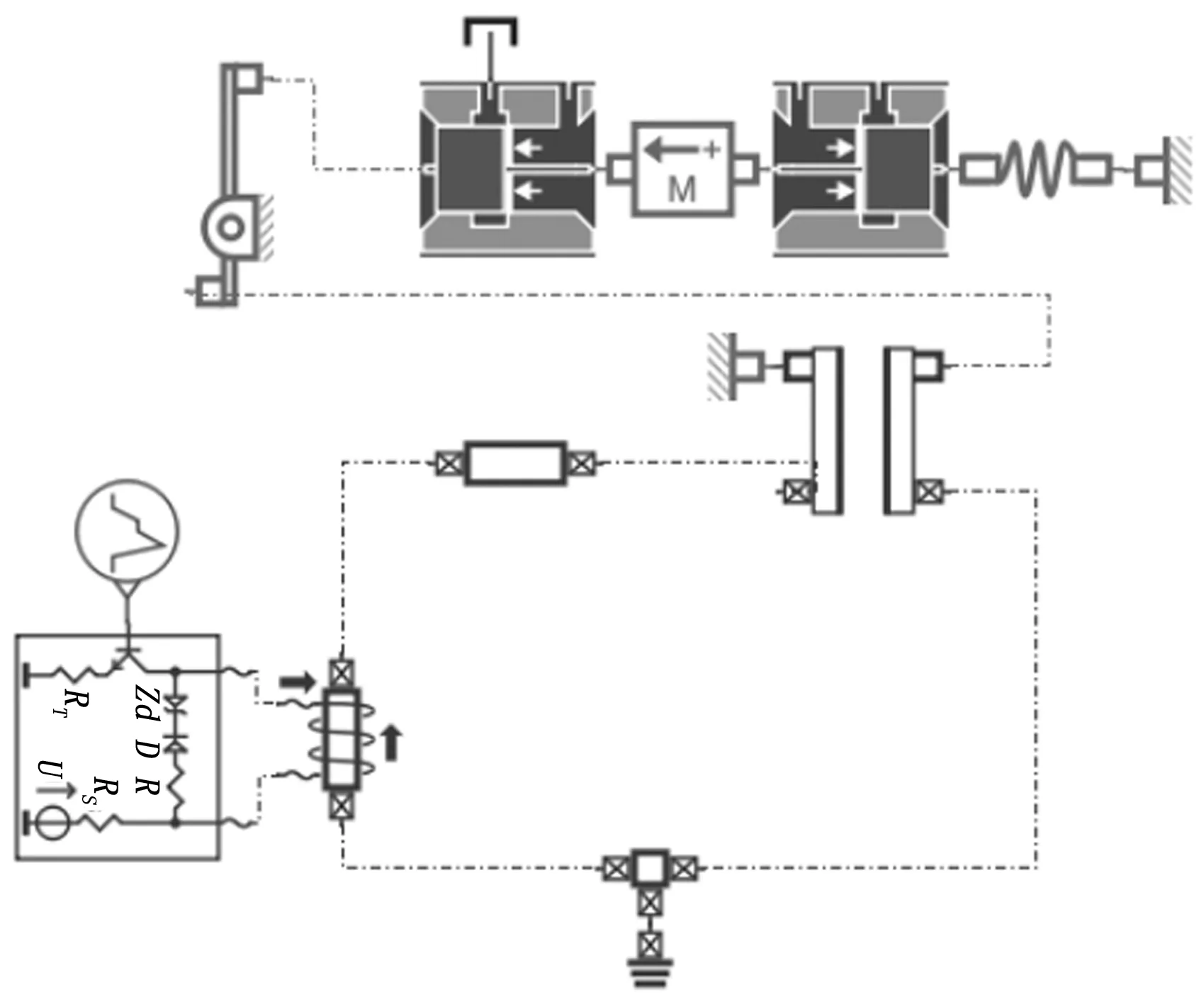
图4 电磁阀模型
建立好电磁阀仿真模型后,按图5 给出开关电磁阀的输入信号,其中0~0.125 s为通电状态,0.125~0.25 s为断电状态。

图5 开关电磁阀的输入信号
表2是电磁阀的主要参数,将下面参数输入到仿真模型中进行仿真。
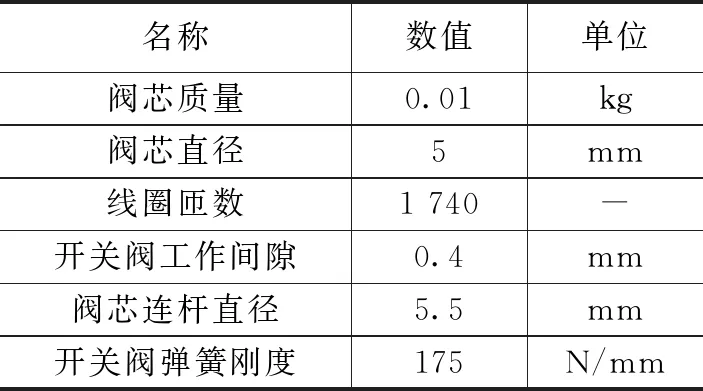
表2 仿真模型主要参数
电磁阀正常状态下开启时驱动端电流波形如图6所示;电磁阀驱动端电流与阀芯位移对比如图7所示。
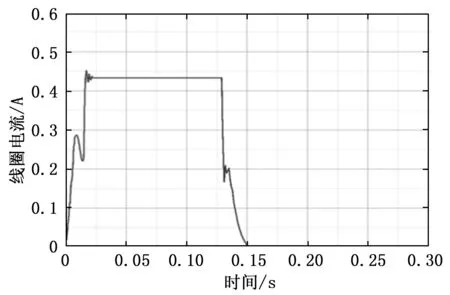
图6 电磁换向阀驱动端电流
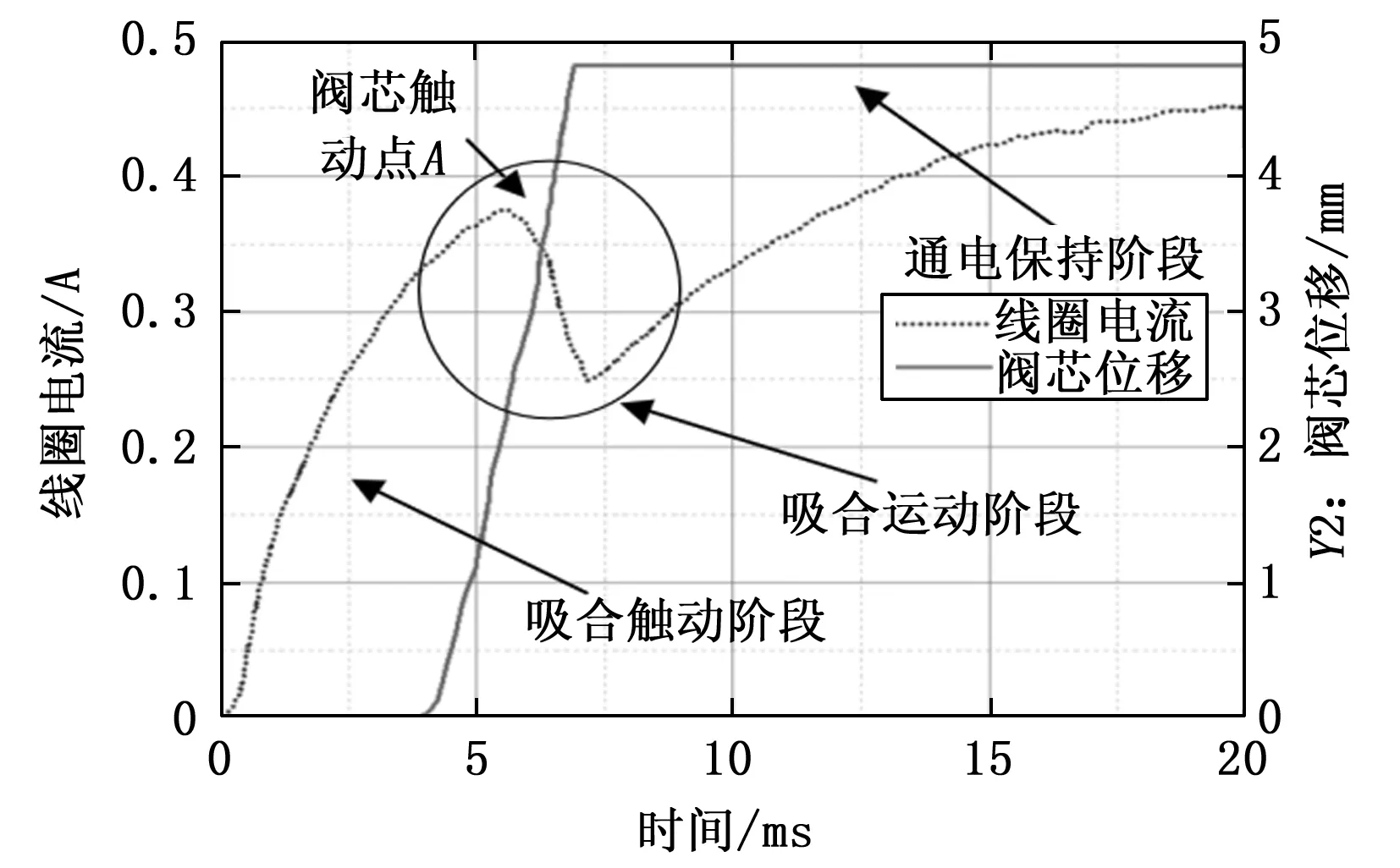
图7 电磁阀驱动端电流与阀芯位移对比图
通过该仿真结果可以得到如下结论:
1)在电磁阀没通电时,没有电流通过,此时的阀芯不运动。
2)当电磁阀通电时,由于绕线式电路中有线圈自感的存在,驱动端电流上升时不能够瞬间稳定到稳态值。此时,回路中线圈所产生的电磁力不足以克服弹簧的反作用力以及阀腔两侧之间的摩擦力。因此,阀芯仍处于静态,为吸合触动阶段。
3)如图7所示,当驱动端的电流逐渐增加到滑阀移动点A时,线圈产生的电磁力可以克服滑阀上的反作用力,滑阀开始移动。位移x不断增大,电感L增加,dL/dt增加。此时,由于阀体的运动速度小,驱动端电流的上升斜率开始降低,因此驱动端电流的上升斜率开始减少。 随着阀体速度的增加,电流略有下降。 该电流变化阶段对应阀芯的吸合运动阶段。
4)当电磁力使得阀芯运动到最大位移处时,阀芯停止运动,线圈的自感系数也不再变化,线圈电流单调上升并趋于稳态,此时为阀芯运动的通电保持阶段。
通过上述仿真中驱动端电流与阀体位移之间的分析,判断阀体的运动状况可以通过其驱动电流的状况反馈,验证了基于驱动端电流的电磁阀特性进行故障诊断的可行性。
2 数据采集方案设计
本节通过设定不同的故障,对电磁阀进行结构上的破坏来模拟电磁阀真实情况下不同故障,从而得到实际电磁阀不同故障的驱动端电流数据。
2.1 实验系统搭建
工况模拟实验台包括电磁阀、转换电源、工作装置控制器组成,数据采集系统采用NI USB 6218数据采集板卡、霍尔电流传感器以及上位机组成。实验过程中使用电源为工作装置控制器供电,将直流电转换成阶跃信号输出,并驱动不同工况电磁阀工作,通过电流传感器采集电流信号,并通过NI数据采集卡采集之后传输到上位机中。实验流程如图8所示。
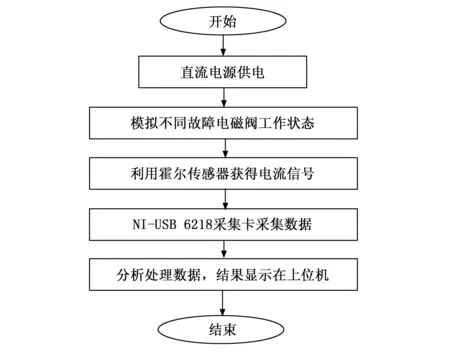
图8 实验系统流程图
2.2 故障特征分析
对电磁阀健康状态、阀芯卡滞、弹簧失效、线圈异常4种状态分别进行模拟故障实验,获取电磁阀健康与各故障状态下的驱动端电流曲线。经过处理后的电流曲线如图9所示。
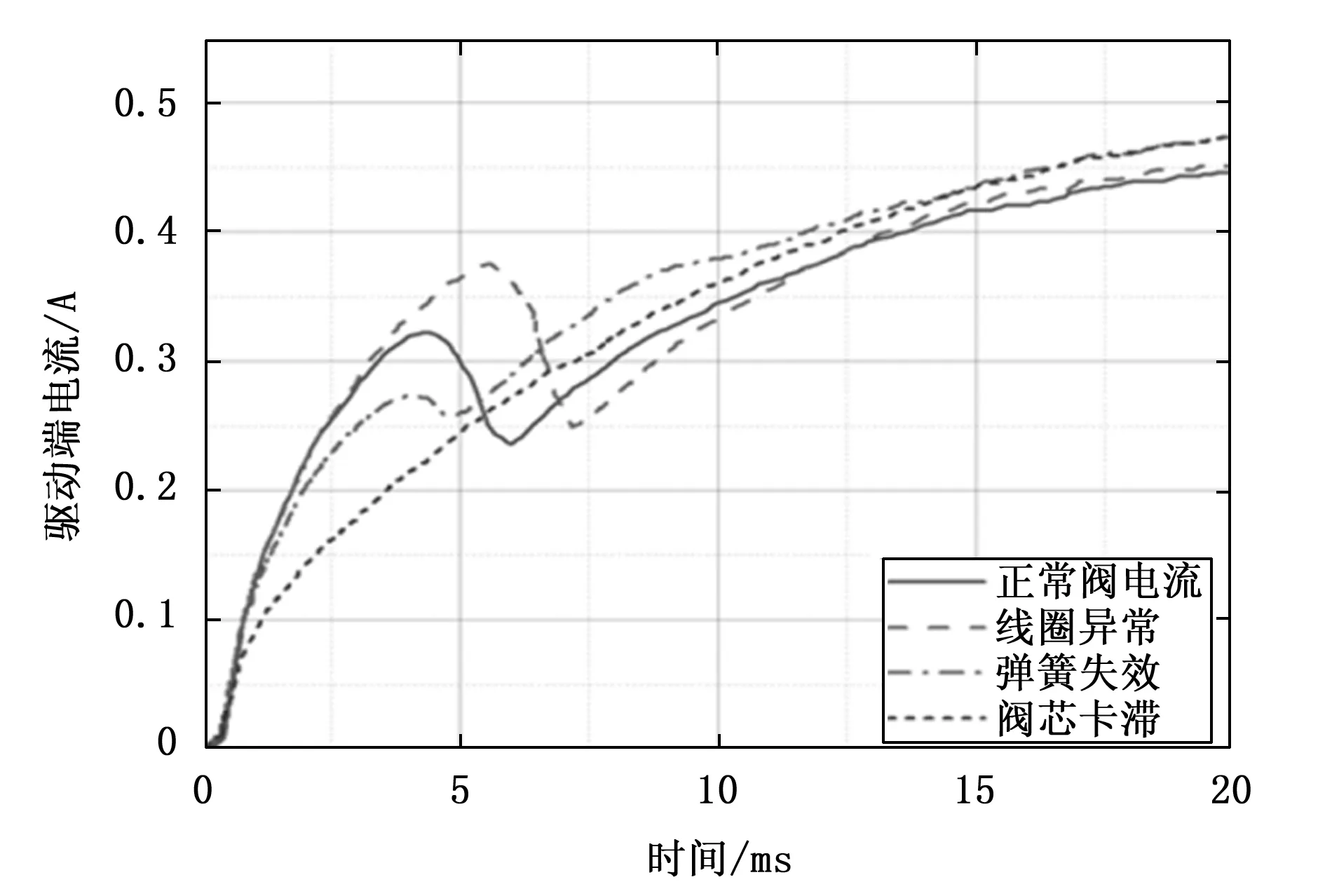
图9 电磁阀各工作状态电流曲线
结合图9,对电磁阀故障情况下的电流变化情况进行对比分析,分析结果如下:
1)当出现阀芯卡滞故障时,阀芯运动所要克服的摩擦力增大。由图分析可知,电磁阀阀芯卡滞故障时,驱动端电流波形的拐点不明显甚至消失,电流变化曲线变化速度比正常阀快。当阀芯卡住时,电流曲线趋于单调上升,这也是摩擦力增加的原因。
2)弹簧发生故障时,阀体无需克服弹簧反作用力或反作用力下降时,在相同电磁力下,阀体运动速度上升,从图中可以发现,弹簧发生故障时,电磁阀驱动端电流比在健康状态下比驱动端电流曲线在第一拐点有明显下降的趋势。
3)当电磁阀出现线圈绕组绝缘材料损坏的故障时,相邻绕组之间发生短路,线圈电感降低,使响应时间和电流曲线变化更快。
收集到的电磁阀驱动端电流分析表明,当电磁阀在健康状态下驱动时,在阀体移动到最大长度之前,阀体的运动速度持续增加,使得电磁回路中的所感应到的电动势逐渐增加,电流信号突然振动出现拐点。 因此,通过检测驱动端的电流变化率,能够提取电磁阀的故障特征信号。
2.3 故障特征量提取
频域分析法是研究控制系统的一种工程方法。该方法的显著优点是引导分析从信号的表面到其本质,揭示信号的组成成分。这一点很重要,因为了解信号的结构可以使其得到最佳利用。频域分析方法也有缺点,不直观,难以理解。获取频谱或将频谱还原为时域信号需要计算,其正弦波分量不能反映其发生的时刻。针对时域和频域分析方法的不足,提出了时频分析方法。该方法显示了信号能量在二维时频平面上的分布情况,适用于非平稳信号。
小波包分解技术可以将任意信号正交分解为独立的频带,利用能量故障特征值提取方法,建立电磁阀驱动端电流的各频带能量特征值与电磁阀不同故障状态的对应关系,利用各频带能量值统计的特征向量的形成能够有效地映射电磁阀的状态。驱动端电流利用db3小波基函数[14]进行三层小波包分解,如图10所示。
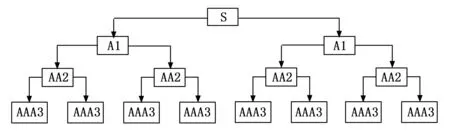
图10 小波包分解示意图
由于采集电流波形在驱动前端存在拐点,基于突变特征选择小波包分解对驱动端电流进行初步分析。通过仿真,分别采集了阀芯卡滞、弹簧断裂、线圈异常和健康状态下驱动端电流各300个数据,从不同状态中截取280个数据作为信号序列的分析计算。使用小波包db3基函数对不同状态的信号在Matlab软件分解成8个频段,有明显区别频段部分如图11所示。
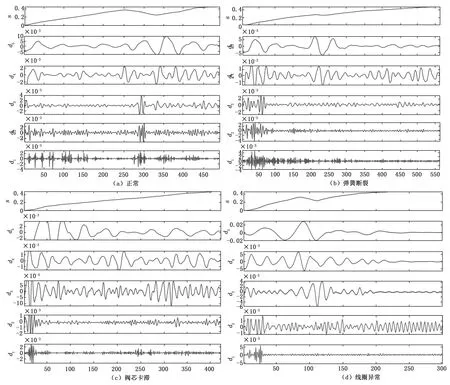
图11 小波重构信号
提取各频段信号的总能量,根据电磁阀故障时驱动端电流各频段能量变化的特征归一化各频段能量,将归一化能量值作为故障类型的特征值。设原信号为S,j表示小波包分解层数,i表示小波包分解节点数,Sj,i表示重构的第j层第i个节点信号,则信号Sj,i对应的能量值Ej,i可表示为:
(5)
其中:j为分解层数,M为离散点个数。第j层的总能量Ej表示为:
(6)
根据各频带所含能量与该层能量总和的比值,构造一个特征向量Tj:
[Tj,0,Tj,1,…,Tj,2j-1]
(7)
原信号被三层小波包分解成8个不同频段的信号,对其进行特征提取,并根据各频段能量与第三层能量总和的比值构造特征向量Tj;根据式(7)求得各故障模式下能量特征向量如表3所示。
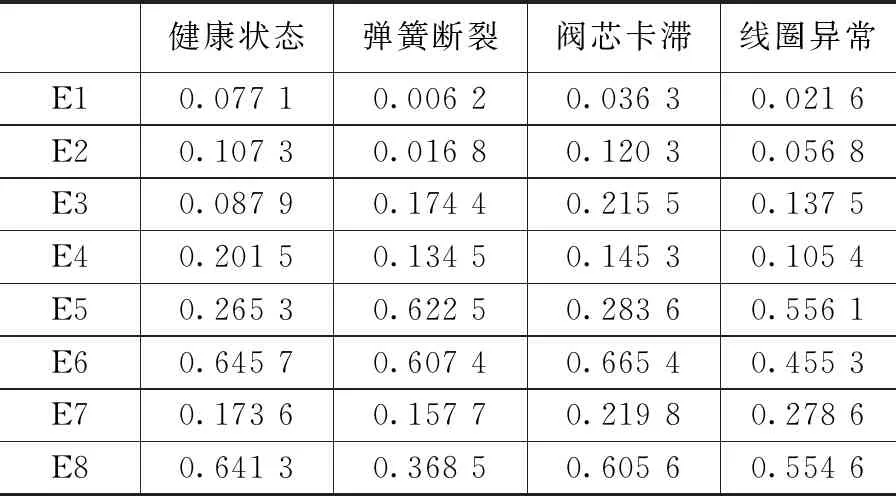
表3 各工作状态下能量值
因此根据式(7)对3种情况下所提取信号进行三层小波包分解、信号重构、能量特征向量提取,将其保存。因此,E1~E8所提取的能量值可作为样本的属性参数[15],将这8个参数作为条件属性。表中第一行是各样本故障类型,作为决策属性。为下一步故障诊断做准备。
3 故障诊断
本节基于提取的小波能量熵作为样本的属性参数,使用邻域粗糙集从原始属性中选择敏感属性作为C4.5的输入属性进行训练;最后,得到故障诊断模型,对故障进行识别。
3.1 基于邻域粗糙集的约简算法
粗糙集理论的核心是在保持知识库分类能力不变的前提下进行属性约简,得到属性“核”,这将有利于摒弃不相关或冗余的数据,降低数据处理的时间和空间复杂度[12]。
定义邻域决策系统NDS=
设
对于邻域决策系统NDS,D将U划分为N个等价类:X1,X2,…,XN,B⊆A生成上的邻域关系NB,那么决策D关于B的邻域下近似和上近似分别为:
(8)
(9)
其中:
(10)
(11)
计算决策属性D对条件属性B的依赖度为:
γB(D)=|POSB(D)|/|U|
(12)
式中,POSB(D)为决策D关于条件属性B的邻域值;U为实验样本集。
然后选择合适的邻域值计算各属性的依赖度。通常情况下,邻域大小可根据下式确定:
(13)
其中:Std(xi)表示属性xi的标准差,λ是设定的参数,不同的λ对应不同的邻域直径,一般λ取值在2~4之间。
依赖度反映了系统中能够被正确分类的样本比例,显然 0≤γB(D)≤1。正域越大,则条件B对决策D的描述能力更强。
设a∈B,则属性a对B的重要度为:
SIG(a,B,D)=γB(D)-γB-a(D)
(14)
经过计算各属性的依赖度与各属性重要度,基于变精度模糊邻域粗糙集[16]得到属性约简算法输出的最佳约简向量子集为B={E3,E8}。
3.2 C4.5决策树算法
由3.1结论可知,选择{E3,E8}作为约简后的条件属性,进行决策树构造。将E1~E8这8个参数作为条件属性。分别对应不同工作状态:F1(健康状态)、F2(弹簧断裂)、F3(阀芯卡滞)、F4(线圈异常)。
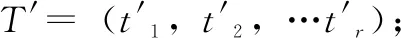
(15)
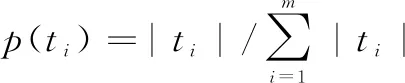
通过将训练集除以属性获得的信息熵如下:
(16)
其中:P(di|aj)表示属于aj分区中的样本属于理想分区T′中的子集dj的概率。
属性A的信息增益[18]为:
HGain(T′)=H(t)-HA(T′)
(17)
属性A的信息增益率[19]为:
(18)
信息增益率越大意味着对结果诊断的重要性越大,经过公式(15)~ (18)计算后,E8、E3属性的信息增益率分别为0.792、0.536。
3.3 故障诊断
基于3.2节内容,进行液体电磁阀故障诊断之前首先对电磁阀不同故障进行模拟。模拟的电磁阀故障类型如表4所示。

表4 故障模拟方式
按表4的方式对电磁阀故障模拟后,利用数据采集系统得到总共得到100个样本数据。
训练样本数据。采用十折交叉法[20-21]验证决策树的诊断准确性。首先,将数据随机分为10组,使用9组随机样本作为训练数据,其余数据作为检测数据对系统进行验证。迭代训练取平均值并将其放置在等宽区间内作为决策树算法的估计。
从3.2所得信息增益率可知,“E8”信息增益率最大,可作为根节点,由表3可以看出,当描述属性 E8时的样本子集对应弹簧断裂故障类别,因此,可以将其作为叶结点,同理,可描述E3对应的故障类别并生成叶结点[22]。
经过C4.5算法进行计算,所构造决策树如图12所示,分别为约简前的样本数据构建的决策树与约简后的样本数据构建的决策树。
虽然属性约简前后生成的决策树的大小和叶子节点的数目一致,但属性约简前生成的决策树使用了其中3个属性,而约简后仅使用2个属性进行建树。对决策树叶节点进行读树,可得该故障样本子集的规则如表5所示。
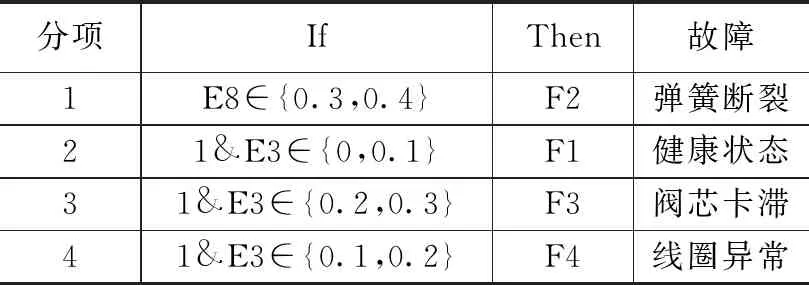
表5 规则集
由表5可知,第一条规则“if E8∈{0.3,0.4} then F2”,表示如果所提取的电磁阀特征能量值E8小于0.4大于0.3,则可能是发生弹簧断裂故障。同理,第三条规则“if 1&E3∈{0.2,0.3} then F3”,表示如果电磁阀能量值在E3大于0.2小于0.3且能量值E8大于0.3小于0.4,电磁阀可能发生阀芯卡滞故障。
每一条规则对应着一种电磁阀故障诊断分类。将检测数据送入系统进行验证,并将约简前与约简后得到诊断结果对比如表6所示。
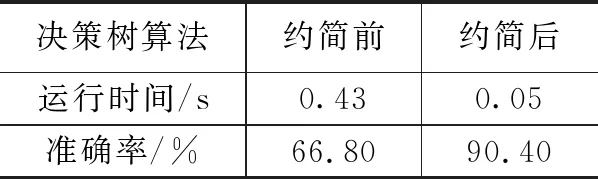
表6 诊断结果
从表6可得,经过C4.5算法进行计算,8个属性减少为2个,得出了分类规则,根据简化前后的诊断结果,提高了基于变精度模糊邻域粗集约简的决策树运行效率。而且经过迭代训练,该故障诊断方法的准确率达到90%,高于约简属性前的决策树。以上结果表明,该方法可对电磁阀进行快速有效的故障诊断。
4 结束语
本文以驱动端电流检测方法为基础,对电磁阀故障诊断问题进行了研究。主要结果如下:
1)提出基于小波能量熵和粗糙集理论的液体电磁阀故障诊断方法。模拟电磁阀健康状态、弹簧故障、阀体堵塞、线圈异常4种状态,利用电磁阀驱动端电流信号变化率进行故障诊断。
2)通过小波包分解对电磁阀不同状态驱动端电流变化率进行分解,得到各频段能量值。将提取的能量值作为故障特征值并保存,为故障诊断做准备。
3)采用可变精度模糊邻域粗集约简算法简化连续数值属性,提高了系统运算效率。 最后,利用约简后的样本数据构造决策树。 经过训练,该模型诊断准确率高达90%。
4)提出的电磁阀故障诊断方法实现了电磁阀的快速诊断,降低了维修与维护成本,具有重要的社会效益和经济效益。
