激光粉末床熔融成形仿生梯度多孔结构弯曲性能*
2023-10-28张明康邓铭坚范宏熙
张明康,邓铭坚,张 颖,范宏熙,王 迪
(1. 广东海洋大学,阳江 529500;2. 华南理工大学,广州 510000)
梯度材料结构在生物材料结构中是一种常见的材料分布模式[1],在动物骨骼[2]、鳞甲[3]和植物枝干[4]等生物材料结构中广泛存在。梯度材料结构往往具有优异的力学性能和能量吸收特性,为轻质、高强、冲击吸收等结构设计提供了设计启发灵感。
梯度材料结构的设计需要研究生物材料结构的材料分布模式。Drol 等[5]通过试验观察和模拟分析研究了刺猬的刺的弯曲行为,发现刺猬刺的内部结构特征是一种梯度变化的结构,其孔隙率由芯部至四周逐渐减小,内部的微结构以垂直于刺壁的方向为主进行分布,该梯度结构的布局极大增加了刺的抗弯性能,同时该结构的发现揭示了一个自然界很有效的结构分布模式。郑伟[6]采用CT 扫描和逆向工程建模技术重建了头骨模型,利用有限元分析方法对头盖骨多孔结构的弯曲性能仿真,发现裂纹在头骨的松质骨脆弱部位萌生,接着向密质骨部位扩展,当密质骨发生断裂时,则结构整体失去了承载能力;从不同方向对头骨进行加载,发现头骨的力学性能具有各向异性,且不同方向上加载的破坏模式也有所不同。竹子由于其独特的功能梯度结构成为了仿生结构设计的理想结构之一,该梯度结构的弯曲行为具有不对称性[7]:当弯曲加载在高纤维密度位置时,其弯曲应力较高,但是挠度较低;当弯曲加载在低纤维密度位置时,弯曲应力较低而挠度较高,微观结构特征的梯度分布引起了竹子的力学性能宏观不对称行为。Song 等[8]利用高分辨率原位力学表征技术研究了竹子的弯曲断裂失效机制,发现竹子的分层微结构在裂纹交替扩展中起到关键性作用,并进一步对竹子的不对称行为进行了定量特征研究,为梯度多孔结构的设计提供参考。
通过模仿梯度材料结构的分布模式,可实现仿生梯度结构的设计,使得结构获得生物材料的优异性能。常见的仿生梯度结构类型主要包括梯度晶格点阵结构、梯度随机多孔结构及梯度极小曲面结构等。梯度晶格点阵结构是通过模仿金属晶格点阵的分布模式,如体心立方、面心立方和简单立方等,并利用梯度函数驱动对各顶点的连线进行包覆管状结构建模,获得微杆直径具有梯度大小分布的空间微结构[9]。而梯度随机多孔结构则是在Voronoi 理论的随机多孔结构基础上,对随机多孔结构的随机性利用特定方向的梯度设计程序进行干扰,使其在随机结构的基础上具有一定的梯度分布[10]。梯度金属晶格结构虽然可以通过参数化方法实现快速设计,但是由于其设计基础是基于金属点阵模式,其桁架结构连接处为突变的尖角结构,存在着应力集中,易导致结构的局部力学性能较差而发生局部断裂现象。梯度随机多孔结构的拓扑几何更接近人体骨骼的松质骨到密质骨的分布模式,需要对仿骨小梁尺寸和孔洞尺寸的极限值进行控制,避免出现无法满足制造工艺要求的微结构。梯度极小曲面结构是基于三周期极小曲面结构(TPMS)设计发展而来的,常见的三周期极小曲面结构包括Gyroid、Diamond、Primitive 和I–WP 4 种结构[11]。上述极小曲面结构可通过隐式三角函数生成,由于其具有光滑连续、高比表面积、内部互联互通的曲面结构,在轻量化结构应用方面具有更大优势。其中Gyroid 结构是极小曲面中研究最为广泛的结构,通过研究其力学、声学等性能,发现其表现出优异的能量吸收性能[12]、高疲劳寿命[13]和声学吸收性能[14]。在均匀极小曲面结构设计基础上,可通过增加控制结构孔隙率的梯度函数,如线性函数[15]、三角函数[16]等,实现线性梯度结构和非线性周期函数梯度结构极小曲面的快速设计。梯度Gyroid结构的压缩曲线呈现阶梯上升的趋势,与均匀Gyroid 结构等均一孔隙率的多孔结构压缩曲线的单一屈服平台不同[17],梯度Gyroid 结构具有更优的能量吸收性能和力学性能。
除了基于常见函数驱动的极小曲面结构设计方法外,Li 等[18]还在变密度拓扑优化结构材料密度基础上,利用插值方法建立材料密度与Gyroid 极小曲面的孔隙率的映射关系,获得了梯度极小曲面多孔结构,并实现了无人机机臂结构的轻量化设计,该梯度多孔结构使结构的最大冯米塞斯应力降低到原来均匀多孔结构的26%。对于医学植入体,如股骨柄、膝关节假体等,除了轻量化需求外,还要求结构具有大量的微结构以提供环境给骨细胞和毛细血管进行生长,因此基于拓扑优化的梯度多孔结构被认为非常适合于医学植入体的设计。Arabnejad[19]和Wang[20]等结合拓扑优化算法和梯度晶格结构设计方法,设计了基于股骨柄拓扑材料密度分布的梯度晶格结构,分别将骨质流失量减少25%和41.9%,降低了骨折和翻修手术的风险。
仿生梯度材料结构由于具有复杂的空间结构且一般单元尺寸结构较小,难以利用传统加工工艺(铸造、锻造、铣削等)成形,而增材制造技术的发展则在仿生梯度材料结构制造方面展现出极大优势。激光粉末床熔融(Laser powder bed fusion,LPBF)技术是激光增材制造技术的一种,其成形原理是采用逐层铺粉的方法,利用高能量激光光束沿着扫描路径使合金粉末经历熔化–凝固过程,结构逐层堆叠,从而实现金属零件的快速成形,可获得精度较高的金属仿生微结构。已有学者对LPBF成形的均匀多孔结构的弯曲性能进行了相关的研究。Tian 等[21]利用LPBF 技术制备了AlSi10Mg 正八面体多孔三明治结构,发现其结构的弯曲强度与相对密度呈现线性函数关系,且裂纹源由底板中间部位产生;Bartolomeu 等[22]研究了LPBF技术成形的Ti6Al4V 简单立方多孔结构的弯曲性能,发现其多孔结构的弯曲弹性模量接近密质骨的弹性模量;但是针对LPBF 成形的梯度极小曲面方面,主要是集中研究其压缩性能和准静态能量吸收性能[23–25],对于LPBF 成形的梯度极小曲面的弯曲力学行为及其失效机理研究较为缺乏。
本研究提出通过模仿竹子结构梯度模式设计梯度极小曲面结构,并结合变密度拓扑优化方法实现拓扑梯度多孔结构设计,利用LPBF 技术制备上述几种梯度极小曲面结构,通过弯曲试验和数字图像相关技术(Digital image correlation,DIC),研究结构孔隙率、孔隙率梯度分布模式等结构因素对仿生梯度材料结构的弯曲行为的影响,为高性能抗弯轻量化结构设计提供参考。
1 试验及方法
1.1 均匀Gyroid 弯曲结构设计
本研究所有模型均采用课题组开发的MATLAB 代码进行结构设计,其中,生成Gyroid 的隐式函数见式(1),FGyroid是Gyroid 的曲面结构函数。
式中,a 为单元体尺寸大小,mm;t(x,y,z)为可控制多孔结构的相对密度变化参数。
建立设计参数t 与多孔结构的相对密度的关系,如图1(a)所示,根据该函数关系设计了孔隙率70%~90%的多孔结构,多孔结构的设计空间为70 mm×10 mm×10 mm,单元体尺寸大小为2 mm×2 mm×2 mm,并在上下底面设计0.3 mm 厚的面板,其结构编号见表1,设计模型见图1(b),模型局部放大图见图1(c)。

图1 均匀Gyroid 结构设计Fig.1 Design of uniform Gyroid structure
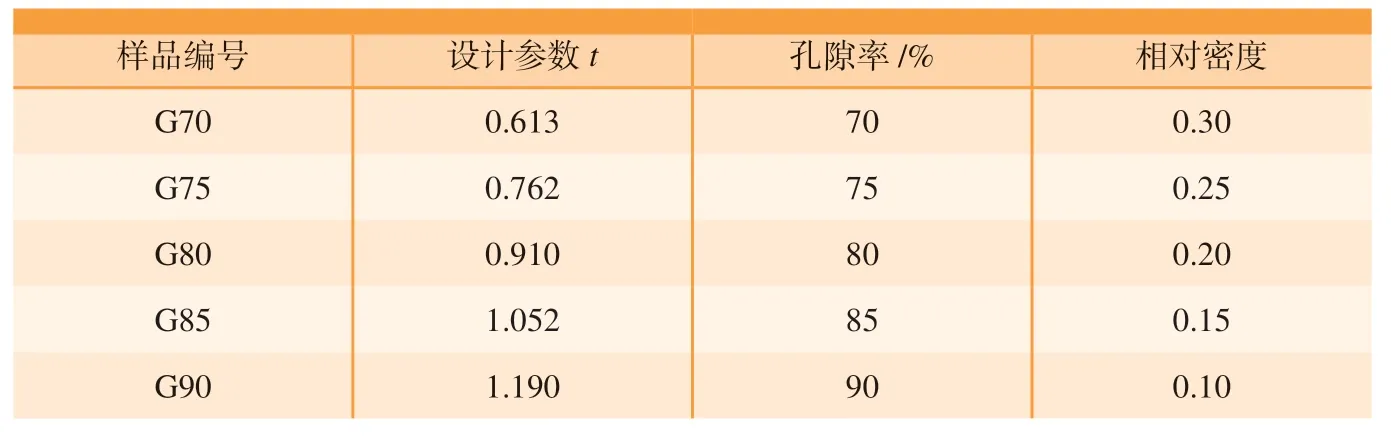
表1 均匀Gyroid 结构设计参数Table 1 Design parameters of uniform Gyroid structure
1.2 线性梯度Gyroid 弯曲结构设计
该梯度结构设计参考竹子梯度结构分布模式,见图2[26],并基于设计参数t 值与Gyroid 相对密度的关系函数及梯度变化控制需求,计算出线性梯度结构的设计函数,如表2 所示。在MTLAB 中将结构梯度控制方程代入式(1),得到不同梯度大小变化的线性梯度多孔结构,如图3 所示。当多孔结构孔隙率增加方向与受力方向一致时,称之为正向线性梯度结构(z–axis linear graded,ZLG);当多孔结构孔隙率增加方向与受力方向相反时,称之为反向线性梯度结构(Reverse z–axis linear graded,RZLG)。ZLG 结构的孔隙率由结构顶部至结构底部逐渐递增,而RZLG结构的孔隙率由结构顶部至结构底部逐渐减小,其孔隙率分布见表2。

图2 竹子横截面的梯度结构[26]Fig.2 Cross section of bamboo showing graded structure[26]
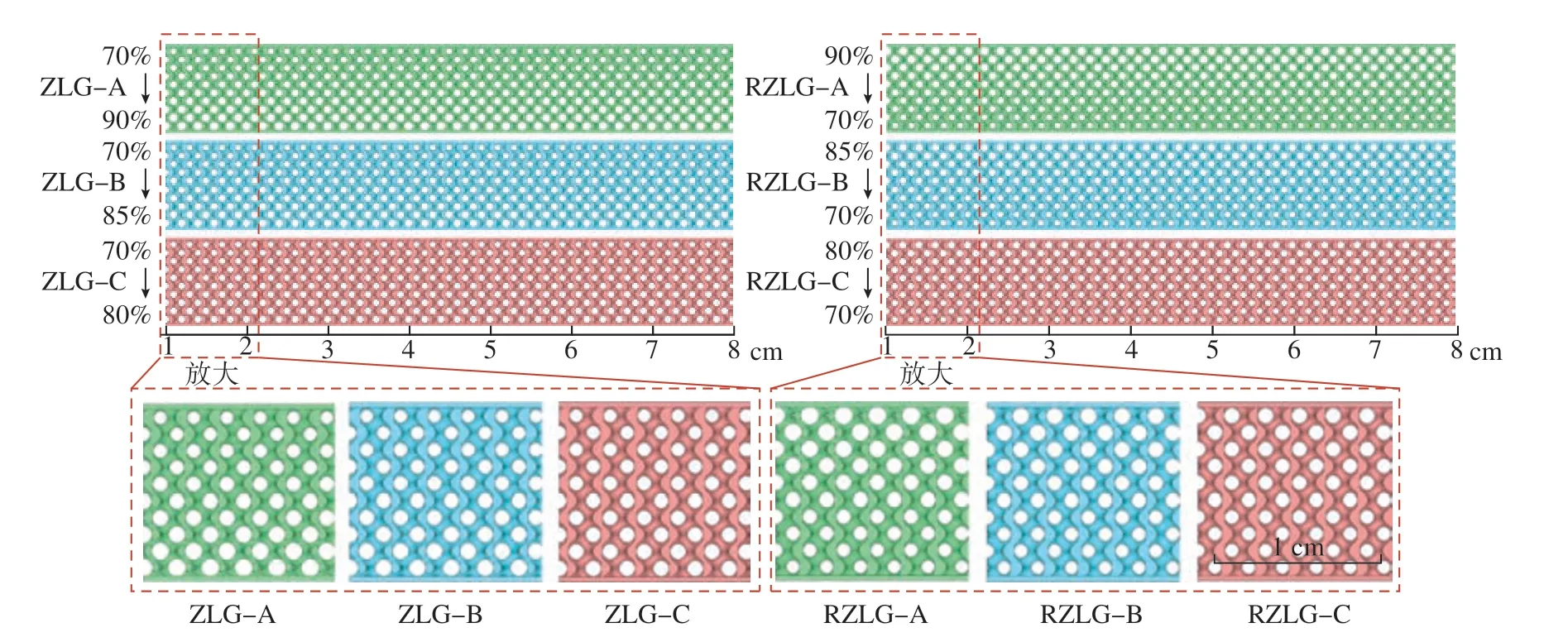
图3 线性梯度Gyroid 弯曲设计模型Fig.3 Design model of linear graded Gyroid for bending test

表2 线性梯度Gyroid 结构设计参数Table 2 Design parameters of linear graded Gyroid
1.3 基于拓扑优化梯度TPMS 弯曲结构设计
基于拓扑优化密度云隐式曲面梯度多孔结构设计方法,是在拓扑优化设计方法基础上进一步对结构进行轻量化与自支撑结构设计,以三点弯曲受力模型为例,其具体设计流程描述如下。
(1)输入.STEP 格式的设计零件,模型为长方体70 mm(长)×10 mm(宽)×10.6 mm(高),至ABAQUS,定义材料属性(316L 弹性模量E=187 GPa,采用弹性模型进行优化)。
(2)模拟三点弯曲试验,在距离中心位置左右各25 mm 处设置固定约束(U1=U2=U3=UR1=UR2=UR3=0),并在顶部中间区域施加z方向的集中载荷F=100 N;对模型进行网格划分(网格尺寸设置为1 mm,网格类型选择六面体网格)。
(3)利用ABAQUS 结构优化模块Tosca 进行拓扑优化分析。定义设计区域为上述的长方体模型,定义材料密度范围为0.1~0.4;设置优化算法,本节中选择基于变密度法的SIMP 算法进行优化计算;设置SIMP 的惩罚值p=3,可通过调整惩罚值从而调整梯度结构的材料分布;创建设计响应,分别设置应变能响应和体积响应;目标函数设置为应变能最小;定义约束函数,约束函数的目标体积小于或等于初始体积的67%;创建拓扑优化进程,提交作业进行优化计算分析。
(4)完成拓扑优化计算后,输出拓扑优化结果中的拓扑优化材料密度与坐标信息,如图4(a)所示,并在MATLAB 中利用csvread 读取信息文件,建立材料密度与t 值的关系函数,利用三次插值函数“interp3”拟合函数F(x,y,z,t)。

图4 Topo–G 结构模型设计Fig.4 Design of Topo–G model
(5)利用MATLAB 代码生成梯度多孔结构,并输出.obj 文件,将.obj文件转换为.stl 文件,并打印测试。
(6)结构通过承载测试,则输出优化梯度模型;如未通过承载测试,则返回至拓扑优化阶段,通过修改惩罚值和材料密度范围进行下一次循环优化。
基于上述流程,获得的拓扑优化Gyroid 梯度多孔结构(Topology graded,简称Topo–G)的总孔隙率为67.34%,见图4(b),其微结构Gyroid 单元体的孔隙率随着材料密度云的分布变化而变化,材料密度高的部位孔隙率较低,材料密度低的部位孔隙率较高,并且实现不同孔隙率之间的结构平滑过渡。
1.4 LPBF 制备弯曲试验试样
利用激光粉末床熔融成形装备(Dimetal–100H,广州雷佳增材科技有限公司)制备Gyroid 弯曲结构,其成形工艺参数:激光功率170 W、扫描速度1000 mm/s、铺粉厚度0.03 mm、扫描间距0.07 mm。所使用的粉末为316L 不锈钢粉末(中航迈特粉冶科技(徐州)有限公司),粒径分布范围为15~53 μm(D10=18.5 μm,D50=34.5 μm,D90=52.7 μm),其元素含量见表3。基于上述工艺参数,利用LPBF 技术制备成形的Gyroid 多孔弯曲结构见图5。

表3 316L 粉末化学成分Table 3 Chemical composition of 316L powder

图5 LPBF 制备的弯曲试样Fig.5 Specimen for bending test manufactured by LPBF
1.5 弯曲试验
多孔结构的弯曲力学性能测试参考中华人民共和国黑色冶金行业标准YB/T 5349—2014《金属材料弯曲力学性能试验方法》,采用电子万能试验机(CMT5105,珠海市三思泰捷电气设备有限公司)进行弯曲试验分析,每种多孔结构使用3 个重复试样进行测试,其施力辊的移动速率为2 mm/min。压辊直径为20 mm,支撑辊直径为20 mm,则支辊间距离l 为50 mm。跨距Ls为50 mm,试样高度h 为10.6 mm,上下板厚均为0.3 mm,试样宽度b 为10 mm,试样长度为70 mm。将多孔结构看作一种低密度实体材料,试样截面对中性轴的惯性矩I 和试样的抗弯截面系数W 的计算公式分别为
弯曲弹性模量E 和弯曲强度σ通过式(4)和(5)计算,其中为弯曲曲线的斜率,Fmax为最大弯曲力。当弯曲测试过程不出现断裂,参考塑性材料的弯曲强度计算方法,将挠度为1.5 倍试样厚度时的弯曲应力作为最大弯曲强度,在本研究中,即当挠度为15.9 mm 时的弯曲应力为最大弯曲强度。
1.6 DIC 测试
使用DIC 测试仪(3D–micro–DIC,法国HOLO3 公司)分析TPMS结构弯曲变形机理,如图6 所示。需要预先在TPMS 的微杆表面上利用喷漆瓶喷涂黑色随机微细斑点,用于DIC 数据采集分析。在电子万能试验机进行弯曲试验过程中,TPMS 的弯曲行为通过数据采集相机进行拍摄(相机分辨率2448×2048),摄像机采样频率设置为1 Hz,然后在DIC软件中对结构弯曲变形过程的采集图像进行计算分析。为了更准确分析杆TPMS 微杆的变形,需要在初始图像中抠除TPMS 的内部孔洞非感兴趣区域,识别感兴趣区域(Regions of interest,ROI),即TPMS 的微杆部分。为分析TPMS 的变形机理,获得了最大主应变的应变云图。在本研究中,抠除TPMS 的孔洞和无特征区域,对于多孔结构的高精度DIC 分析是非常重要的。

图6 DIC 数据采集分析装置Fig.6 Data collected by DIC equipment
2 结果与讨论
2.1 孔隙率对Gyroid 弯曲性能的影响
不同孔隙率的均匀Gyroid 结构的弯曲曲线见图7(a),分析可知,当孔隙率在70%~80%时,Gyroid 结构弯曲曲线先后经历线弹性阶段、屈服变形平台阶段及弯曲断裂阶段。弯曲断裂阶段可通过弯曲力在特定位移时存在断崖式下降的位置进行判断。随着孔隙率的增加,当Gyroid结构的孔隙率为85%和90%时,其弯曲曲线变化可分为3 个阶段:线弹性阶段、屈服平台阶段及弯实阶段。利用式(4)和(5)对弯曲曲线进行结构弯曲性能分析,获得多孔结构的弯曲弹性模量和弯曲强度,见图7(b),分析可知,Gyroid 结构的弯曲弹性模量随着孔隙率的增加而逐渐减小,而最大弯曲强度则是在孔隙率为70%~80%时,随着孔隙率增加而逐渐减小,但是当孔隙率为85%时,其结构由于无弯曲断裂出现而弯曲强度呈现突变,G85 的弯曲强度比G80 的弯曲强度高108.9%。G70和G90 对应的DIC 应变云图见图8。由DIC 结果分析可知,G70 发生较大塑性变形的位置在结构中上部和中下部,其裂纹源出现在中下部位置A处的面板,并由下至上呈现45°斜角扩展。而G90 结构的DIC 应变云图表明,最大应变位置出现在结构与压辊接触的中上位置,变形向四周逐渐减小,其塑性变形面积较大,且G90不出现断裂特征,与弯曲曲线不出现断裂的特征一致。

图7 均匀Gyroid 结构的弯曲性能Fig.7 Bending properties of uniform Gyroid structure

图8 均匀Gyroid 结构弯曲变形过程中的DIC 应变云图Fig.8 DIC strain nephogram of uniform Gyroid structure during bending deformation
上述结果表明,孔隙率的大小会影响Gyroid 多孔结构的弯曲变形行为,并且存在着临界孔隙率,当结构孔隙率小于该临界孔隙率时,Gyroid结构则会出现弯曲断裂特征。当孔隙率较低时,结构弯曲弹性模量较高,弯曲力随着位移的增加而快速上升,导致芯部结构所产生的弯曲力在较小变形时便处于较高弯曲力状态;根据弯曲结构的应力分布分析,底部结构处于拉应力状态,低孔隙率的多孔结构塑性变形较小,高拉应力状态的多孔结构通过力的传递将底部面板撕裂,从而使面板发生断裂;由于弯曲结构存在着剪切应力,且最大剪切应力位置在底部面板附近,弯曲切应力大小呈现45°分布,从而使内部的多孔芯结构也由断裂源沿着45°快速扩展到芯部上方,使整体结构发生弯曲断裂失效。当孔隙率较高时,多孔结构塑性应变较大,且需要经历较长的塑性屈服阶段才会到达弯实阶段,且高孔隙率多孔结构弯曲力较低,在进入弯曲屈服阶段后便处于缓慢增加模式,在未达到面板的断裂应力前,不会出现弯曲断裂。
2.2 梯度变化方式对Gyroid 弯曲性能的影响
根据线性梯度Gyroid 结构的弯曲曲线(图9(a)),分析获得梯度结构的弯曲弹性模量和弯曲强度(图9(b))。由图9(a)分析可知,所有线性梯度结构的弯曲曲线均存在弯曲断裂特征。线性梯度Gyroid的弯曲弹性模量随着结构总孔隙率的下降而逐渐上升。在相同总孔隙率的条件下,ZLG–A 的弯曲弹性模量比RLZG–A 的弯曲弹性模量高出18.57%,随着梯度程度的减弱,正反向线性梯度结构的弹性模量之差逐渐减小,ZLG–C 的弯曲弹性模量只比RZLG–C 的弯曲弹性模量高出1.66%。该结果说明线性梯度结构的弯曲弹性模量与孔隙率分布模式相关,当低孔隙率分布在与上压辊接触的附近而高孔隙率分布在底部时,弯曲弹性模量相对反向分布模式有所增加,该梯度弯曲结构的比较结果与竹子的梯度结构弯曲行为[7]相似:当纤维密集地分布在上部而稀疏地分散在下部时,具有高弯曲模量;当将上述结构反向弯曲加载时,纤维密集于下部,而稀疏分散在上部时,具有低的弯曲模量,但是也具有较高的挠曲韧性,该弯曲力学性能表现被称为非对称性弯曲行为。

图9 线性梯度Gyroid 结构弯曲性能Fig.9 Bending properties of linear graded Gyroid structure
结合梯度结构弯曲变形DIC 应变云图(图10)对结构弯曲变形模式进行分析。DIC 结果表明,ZLG–A和RZLG–A 在弯曲位移10 mm 前均未出现结构的宏观断裂,说明其具有较高的挠曲韧性;ZLG–A 的大应变区域集中在结构中下部位,为高孔隙率区域,而RZLG–A 的大应变区域则是集中在中上部位靠近上压辊区域,并且出现了明显的面板褶皱和芯层剪切变形。Jing 等[27]对泡沫铝三明治结构弯曲失效过程做了相关研究,认为其具有4 种失效模式,为上面板褶皱、芯层剪切、芯层与面板间界面失效和下面板断裂;Deshpande 等[28]在研究三明治点阵结构的弯曲行为时发现4 种竞争式坍塌行为,包括面板屈服、面板褶皱、芯层剪切和压实。分析该线性梯度结构发现,ZLG–A 和RZLG–A 的弯曲行为均具有面板褶皱,但是只有RZLG–A 具有明显的芯层剪切,且其褶皱变形更为明显。

图10 线性梯度Gyroid 结构弯曲变形DIC 应变云图Fig.10 DIC strain nephogram of linear graded Gyroid structures during bending deformation
当梯度变化差异减小,且结构整体致密度上升后,ZLG–B 和ZLG–C均在结构的底部发生弯曲断裂,且都是从中间撕裂,与G70 的45°剪切断裂方式不同,这是由于在弯曲过程中应力集中在结构底部,导致承载能力低的微杆(孔隙率较高部分)较早发生断裂,形成裂纹源,该裂纹源沿着底部脆弱的部分迅速扩展,从而导致结构弯曲断裂失效。而RZLG–B和RZLG–C 结构在前期较低应力状态下顶部高孔隙率结构已发生塑性变形,在应变逐渐增大后,底部低孔隙率的微结构抵抗变形和断裂能力较强,在整个弯曲过程中无危险裂纹源产生,故不发生弯曲断裂失效。由于RZLG–B 和RZLG–C 结构不发生宏观的弯曲断裂,因此其弯曲曲线呈现逐渐上升的趋势,RZLG–B 结构的弯曲强度比ZLG–B 高出21.88%,RZLG–C 结构的弯曲强度比ZLG–C 高出9.58%;在弯曲位移较大时,RZLG–B 和RZLG–C 的弯曲曲线则呈现局部波动状态,这是由顶部高孔隙率微结构的屈服变形和面板褶皱造成的。
上述结果分析表明,孔隙率梯度分布的模式会影响结构是否出现弯曲断裂:当高孔隙率在结构上方而低孔隙率结构在结构下方时,弯曲结构不会出现弯曲断裂现象;当高孔隙率在结构下方,低孔隙率在结构上方时,总的孔隙率低于一定值时则会出现弯曲断裂现象。
2.3 基于拓扑优化梯度TPMS 结构的弯曲性能
Topo–G 的弯曲曲线见图11,分析可知,Topo–G 结构弯曲过程包括线弹性阶段、屈服变形平台阶段及弯曲断裂阶段,该弯曲曲线特征与低孔隙率的均匀Gyroid 结构相似。Topo–G 结构的弯曲弹性模量为(13.42±0.70) GPa,弯曲强度为(252.15±7.67) MPa,均高于文中所有的线性梯度结构的弯曲弹性模量和弯曲强度。Topo–G 的DIC 应变云图见图12,其应变最大值发生在结构的中间高孔隙率位置,由于该区域微结构的孔隙率较高,承载性能较差,裂纹源由此产生,并沿着孔隙率梯度降低方向进行扩展,最后导致结构的弯曲断裂。由上述分析可知,基于应变能最小的SIMP 拓扑优化方法获得材料密度云,并将该密度云映射设计为变密度的梯度多孔结构,对于结构的弹性模量和弯曲强度的提升均具有一定效果,但是对于挠度韧性则较差,挠度较低。

图11 Topo–G 的弯曲力–位移曲线Fig.11 Bending force and displacement curves of Topo–G

图12 Topo–G 的弯曲变形DIC 应变云图Fig.12 DIC strain nephogram of Topo–G during bending deformation
将本研究所有结构的弯曲弹性模量、弯曲强度和孔隙率的关系进行分析,如图13 所示。利用线性函数对均匀Gyroid 结构的孔隙率与弯曲弹性模量的关系进行拟合,拟合效果较好,说明均匀Gyroid 结构的弯曲弹性模量与孔隙率变化呈现线性相关,弯曲弹性模量随着孔隙率下降而线性增加。但是均匀Gyroid结构的弯曲强度与孔隙率并无明显的函数关系,值得注意的是G85 的弯曲强度在图13 的右上方,说明该结构在相同孔隙率的条件下具有很高的弯曲强度。ZLG–A(总孔隙率为79.72%)的弯曲弹性模量比G80(孔隙率为80%)弯曲弹性模量高出16.74%,ZLG–A 的弯曲强度比G80高出30.91%;其反向线性梯度结构RZLG–A 的弯曲弹性模量比G80 低1.55%,而RZLG–A 的弯曲强度比G80 高出36.08%,该对比结果表明ZLG–A 和RZLG–A 的孔隙率分布模式能大幅度提升结构的抗弯强度,且ZLG–A 的分布模式能同时提升弯曲弹性模量和抗弯强度。随着结构孔隙率梯度变化差异的逐渐缩小,在低孔隙率范围线性梯度多孔结构的弯曲弹性模量和弯曲强度与均匀多孔结构的弯曲性能相近。Topo–G的弹性模量和弯曲强度均在图13 左上方,表明在低孔隙率范围Topo–G的结构具有更优秀的抗弯性能和弯曲刚度。上述结果说明合理的线性梯度和基于拓扑密度分布的多孔结构可提升结构的抗弯曲性能。在已有的相关文献报道中[29],选择性激光熔化(SLM)制备的316L–BCC 多孔结构(孔隙率87%)的弯曲弹性模量为(0.2±0.05) GPa,而本研究中的G90的弯曲弹性模量为(4.97±0.22)GPa,远大于316L–BCC 结构的弯曲弹性模量。SLM 制备的六面体形的Ti6Al4V 多孔结构[17],SP5(孔隙率为78.6%±0.9%)的弯曲弹性模量为11.41 GPa,比本研究中G80(孔隙率为80%)的弯曲弹性模量高出54.88%,其弯曲弹性模量也是随着结构孔隙率下降而上升。
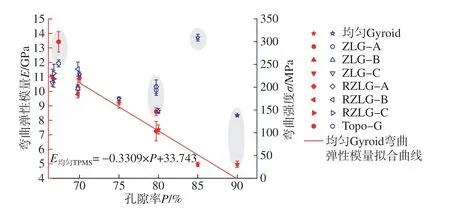
图13 多孔结构弯曲性能Fig.13 Bending properties of porous structures
3 结论
(1)均匀多孔结构Gyroid 的弹性模量与孔隙率的变化呈现线性相关,且存在着断裂临界孔隙率,当孔隙率≥85%时,Gyroid 多孔结构不会出现弯曲断裂;当孔隙率≤80%时,Gyroid 多孔结构在一定弯曲变形后出现45°剪切断裂。
(2)通过模仿竹子梯度结构,利用梯度结构函数设计了线性梯度Gyroid 结构,该梯度结构具有竹子的非对称性弯曲行为,孔隙率以70%→90%形式分布时具有最高的挠曲韧性且无弯曲断裂出现;而当孔隙率梯度差异缩小时,弯曲断裂源出现在结构底部中间并沿垂直向上方向扩展,线性梯度结构的断裂模式与均匀结构的45°剪切断裂模式不同。
(3)基于拓扑优化变密度梯度多孔结构相对于线性梯度多孔结构具有更优的弯曲弹性模量和弯曲强度,证明了可通过合理的梯度孔隙率分布优化结构弯曲性能,为轻质高强抗弯结构的优化设计提供参考。
