概率密度函数在超导重力台站背景噪声中的应用

2023-10-27张凌云薛秀秀田桂娥程海港

华北理工大学学报(自然科学版) 2023年4期

张凌云,薛秀秀,田桂娥,程海港

(华北理工大学矿业工程学院,河北唐山 063210)

引言

超导重力仪(Superconducting Gravimeter,简称SG)是一种高度灵敏且稳定的重力测量仪器,具有低噪声水平、稳定性和广泛的频率响应范围。灵敏度可达1 ngal (0.01 nm/s2),年零漂小于10×10-8m/s2,可以准确监测重力随时间的微小变化,有助于深入了解地球内部结构和各种地球动力学过程[1,2]。SG台站的背景噪声水平是评估观测数据质量和台站观测环境的关键指标,对于台站选址、仪器校准和地球动力学研究至关重要。全球SG背景噪声水平分析为全球动力学信号的探测提供了数据选择依据[3]。通过选择噪声水平较低的SG观测数据,并应用有效的叠加方法,可以进一步降低噪声水平,并有利于提取微弱信号[4-10],Peterson通过分析全球75个地震仪台站的观测记录,得出了低噪声模型NLNM(New Low Noise Model)。NLNM是全球地震仪观测台站噪声水平的下包络线,代表了仪器性能和台站综合条件最佳的地震仪台站的噪声水平[11,12]。背景噪声水平可以从功率谱密度(Power Spectral Density) 中提取,其中简正模频段为200～600 s的平均功率谱密度被称为地震噪声水平(seismologicalnoisemagnitude,SNM)[13]。SNM是描述地震频段噪声大小的无量纲参数,可用来评估台站地震频段噪声水平的高低,SNM值越大,表示地震频段的噪声水平越高[14]。

在研究噪声随功率密度的变化时,通常需要选择没有地震干扰且外部环境干扰较小的时间段进行功率谱密度 (PSD)分析。然而,这种方法的局限性在于无法全面评估台站噪声水平,且工作量巨大。为了解决这个问题,Mcnamara和Raymonnd发展了Peterson的台站噪声模型估算方法,引入了概率密度函数统计法(probability density function,PDF)来分析地震观测台站的噪声水平[15]。使用概率密度函数方法可以保持数据的连续性,并直观地将影响背景噪声的因素体现在概率密度函数 (PDF) 的概率值中。这种方法能够充分反映台站噪声水平的实时变化情况。目前,国际地震台网(IRIS)等机构已将这种方法应用于日常地震仪数据质量跟踪,但在超导重力台站的背景噪声分析方面应用较少。因此,本项目将概率密度函数方法应用于超导重力台站的背景噪声分析,并与传统的背景噪声分析方法进行比较。这将作为评估超导重力台站背景噪声的辅助方法,以提供更全面的评价和分析。通过比较2种方法的结果,可以更好地了解超导重力台站背景噪声特性,并为进一步的研究和数据分析提供重要依据。

1 传统方法分析拉萨台站地震频段背景噪声

选择2012年拉萨超导重力台站采样间隔为1 s和1 min的观测数据,进行预处理并计算SNM:

(1)重力数据标定,将2012年采样间隔为1 s和1 min的连续重力数据分割成单天数据段;

(2)格值转换,将电压值转换成重力值(μgal)和气压值(hPa),图1(a)为拉萨超导重力台站2012年1月份原始重力记录,单位为μgal;

图1 拉萨超导重力台站单日观测数据的功率谱密度

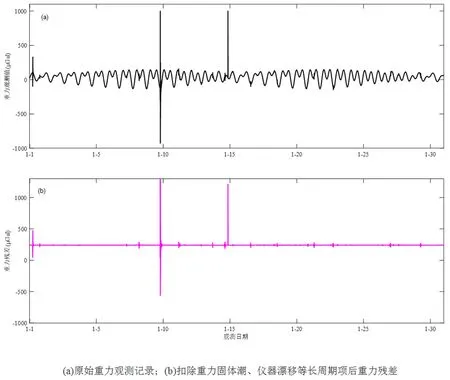
图1 拉萨超导重力台站2012年1月份观测数据预处理

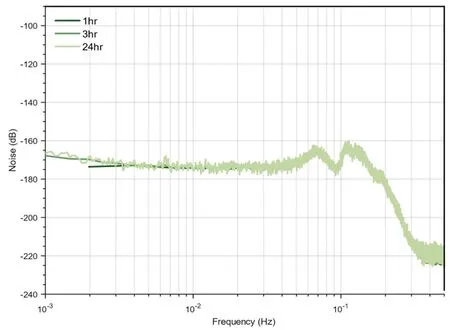
图3 数据长度分别为1h、3h和24h的平均PSD

(3)去除均值和线性趋势;

(4)扣除重力潮汐理论值和改正大气负荷效应,大气导纳值采用的是-0.3 μgal/hPa;

(5)扣除拟合得到的9阶多项式,去除残余潮汐和仪器漂移等长周期项,图1(b)为重力残差;

(6)人工剔除单天异常数据如间断、尖峰、阶跃等;

(7)计算单天重力残差数据的均方根RMS;

(8)选取该月中RMS值最小的5天数据作为该月的平静期数据,对其进行傅里叶分析,获得这5天的平均振幅谱;

(9)对选取的5天平静期数据200～600 s频率范围内的平均功率谱 (mean PSD) 计算作为该月的噪声水平;

(10)根据平均功率谱得到SNM(见式1),其中,PSD单位为μgal2/Hz。新低背景噪音模型(NLNM)为利用超导重力仪计算地震频段背景噪声提供参考和约束,其SNM接近于0。

SNM=log10(meanPSD)+2.5

(1)

由式(1)可得,采样率为1 s的超导重力数据的SNM为1.226,2012年全年最平静5天为323、209、031、100和305年积日(如表1所示),平静期5天的平均功率谱密度为0.053 23 μgal2/Hz;采样率为1 min的SNM为0.909,全年最平静5天为049、006、013、050和322年积日,平静期5天的平均功率谱密度为0.025 66 μgal2/Hz。需要注意的是,采样率为1 min的数据是通过对采样率为1 s的数据进行低通滤波得到的。该滤波抑制了高于Nyquist频率(即1/120 s=8.3 mHz)的能量,导致得到的功率谱衰减更快,因此得到的SNM(0.909)也较低。

表1 基于功率谱概率密度函数方法得到的平静期与传统方法对比

2 拉萨台站背景噪声概率密度函数分析

2.1 计算功率谱密度

为了最大程度地减少重叠后的频谱泄露效应并增加频峰的宽度,对各台各分量的数据进行以下步骤处理:将数据划分为1 h的数据段,在数据段之间进行50%的重叠,这意味着每个数据段将与相邻数据段共享一部分数据,这样做有助于减少重叠效应,并提高数据的连续性和稳定性;将每小时的连续数据分为13个时间段,各段之间进行75%的重叠。这样可以进一步减小重叠效应,并确保频谱数据的完整性;利用FFT(快速傅里叶变换)计算每个时间段的功率谱密度值;对于1 h的PSD值,选取13个时间段的PSD平均值,这样可以得到每小时更加稳定和可靠的PSD值,以用于后续分析和比较;将PSD换算成分贝。

通过以上处理,能够尽可能减少重叠后的频谱泄露效应,增加频峰的宽度,并获得更准确和可靠的功率谱密度数据。这种方法在数据处理中具有重要意义,可以提高数据的质量和可解释性。通过上述方法可产生大量的PSD光滑曲线,进而统计得到台站地震噪声功率谱密度函数。图2所示为拉萨超导重力台站单日观测数据的功率谱密度。以2012年1月2日的拉萨超导重力台站观测数据为例,得到功率谱密度如图 2(a)所示,图中包含了47条PSD最大值、最小值、均值、中值和10百分位统计值,90百分位统计值,其中(PSD)平均值为(橘色直线)、中位数(绿色实线)以及第10(黑色直线)和第90百分位统计数据(黑色虚线)。图2(b)为2012年100年积日拉萨超导重力台站功率谱密度数据,图中包含(PSD)平均值、中位数、第20和第95百分位统计值,灰色区域为平均值±95百分位统计值,由图可知谱密度(PSD)平均值和中位数相差较小,PSD数据的分布比较对称、集中,所以采用平均PSD作为每天的PSD值。

传统评估超导重力仪背景噪声的方法是对一整天的观测数据进行加窗傅里叶变换,然后计算其PSD。将数据长度为1 h、3 h和24 h的平均PSD统计值进行比较(见图 3),可以观察到小时平均值PSD更为平滑,能够反映整天PSD的变化趋势。由于超导重力仪的采样率是1 s,1 h只包含3 600个采样点,因此频率间隔较大,频率分辨率较低。可以认为1 h的数据长度PSD是一天数据PSD的平滑结果。数据长度越长,频率分辨率越高,PSD细节越丰富。地震频段背景噪声关注的是200～600 s的频段,可选择使用1 h的数据长度来计算概率密度函数(PDF),计算频段范围内的PSD平均值。

2.2 计算概率密度函数PDF

对得到的每小时PSD数据,以1/8倍频为单位间隔,滑动计算全频段内的平均功率谱。平均功率值取PSD在Tc处的值

(2)

其中,TS为起始点周期,TL=2×Ts,Ts=Ts×20.125,每次均以20.125倍数增加,滑动计算每一间隔的平均功率值,当TL达到原始数据的最长有效周期停止计算。通过计算可以得到大量的PSD曲线,之后对每条曲线以1 dB为间隔进行频数统计,这样对于某一周期Tc,它的概率密度函数可表示为:

P(Tc)=NPTc/NTc

(3)

其中NPTc是在某个1 dB区间内PSD值总数。NTc是在周期Tc上,所有PSD值的总数。对于给定的周期,利用(3)式可得出某一PSD值的概率密度P(Tc)。即可在周期-功率密度图上将其概率以不同颜色表示,得到功率谱密度概率密度函数 (见图4),色度条表征PSD的概率密度值,范围为0%至30%。通过这种方法能直接反映出噪声的时间变化分布特征。

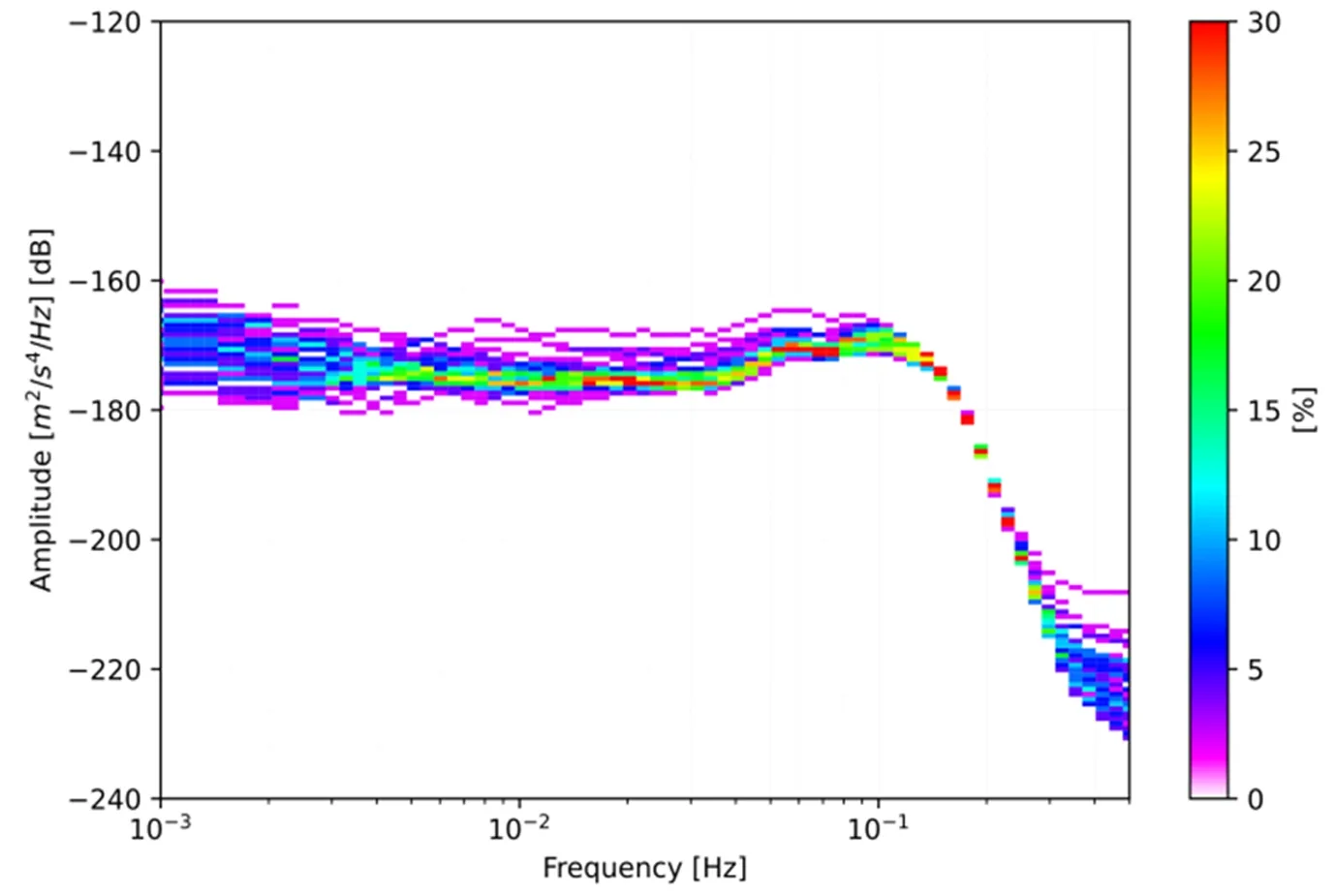
图4 2012年100年积日拉萨超导重力台站功率谱密度(PSD)

为了确认该种方法的准确性,仿照式(1),定义

DNM=log10(PSD)+3.5

(4)

DNM (Daily noise magnitude) 方法是一种用于评估超导重力台站背景噪声的方法。与传统方法不同的是,DNM方法利用每天的所有数据,而不仅仅选择最平静期的天数。这种方法更全面地反映了每天的噪声情况。DNM方法得到的SNM值为0.945(如表2所示),平均功率谱密度为0.027 85 μgal2/Hz,其介于1 s和1 min 2种采样的平均功率谱密度之间且更倾向于1 min。最平静5天为052、050、029、031和014年积日,与1 s和1 min的最平静期分布有交叉。因此,DNM方法可以作为传统评估超导重力台站背景噪声方法的有效补充。通过使用DNM指标,可以更全面地了解每日噪声幅度信息,从而更准确地评估台站的背景噪声水平。