6R焊接机器人轨迹优化及仿真研究

蔡玉强,吴汉文

(华北理工大学 机械工程学院,河北 唐山063210)

引言

工业机器人是实施自动化生产线、智能制造车间的关键设备,为推动我国机器人产业快速、健康的可持续发展,大力发展工业机器人技术势在必行。为提高装备制造现场的产品质量和效率,合理的轨迹规划至关重要。轨迹规划目标是确定一条机器人运动过程中速度、加速度过渡平缓,并保持机器人末端运动状态稳定的轨迹。并在此条件下,针对机器人运行时间进行优化,提高其工作效率。

根据轨迹规划空间不同,其主要分为笛卡尔空间与关节空间:前者直接描述末端执行器的位姿与时间的函数;后者描述的是各关节角度与时间的函数关系,该方法计算量较小,且没有奇异性,十分适用于点对点的运动问题。针对适用对象,该项目主要研究关节空间轨迹规划,当前国内外学者在关节空间轨迹规划及优化领域的研究逐步深入[1],目前主要有多项式插值法[2,3]、组合多项式插值法[4,5]、B样条插值法[6,7]以及是针对此类基础插值算法进行改进。在轨迹规划时常伴随轨迹优化的研究,优化目标主要有时间[8-10]、能耗[11,12]、脉动[13],通常采用各类智能算法来实现以上目的[14]。综上,本文以时间最优为目标,采用改进PSO算法对6R焊接机器人运行时间优化。在任务空间焊接路径上选取路径点,并将其对应的机器人末端位姿映射为关节空间各关节角度值;采用3-5-3多项式对各关节路径点插值,拟合得到关节空间连续运动轨迹;最后,采用递减惯性权重和非线性动态学习因子的PSO算法对该轨迹进行优化计算,得到机器人运行时间最优轨迹,并用MATLAB软件进行验证。

1 机械臂运动学模型

以ABB IRB1660型机器人为研究对象,如图1为机器人运动状态的CAD模型,根据D-H法建立机械臂的各连杆坐标系如图2所示。该机器人均为转动关节,末端夹持焊枪。令基坐标系 坐标系 重合,其余坐标系各方向按右手定则确定。其D-H参数及个关节变量范围如表1所示。

表1 ABB IRB1660机器人D-H参数表

图1 IRB1660机器人三维模型图 图2 IRB1660机器人连杆坐标系

其中,ai-1为连接连杆i-1的相邻两关节轴线的公垂线,即连杆的长度;αi-1为相邻的2个关节之间的扭角,即连杆扭角;di为ai-1与轴线i的交点到ai与该轴交点的距离,即连杆偏距;θi为ai-1与ai的延长线间的夹角,即关节角。

根据D-H表建立该机器人正运动学方程,相邻连杆间坐标转换通式为:

(1)

变换矩阵的一般表达式为:

(2)

将基坐标系{o}至机器人末端坐标系{6}的连杆变换矩阵依次相乘便得到IRB1660的机器人末端夹持机构相对于基座的总变换矩阵为:

(3)

(4)

式中,[n、o、a]分别为机械臂位姿的方向分量;[p]为机械臂的位置分量。通过MATLAB软件来验证机器人运动模型正确性、保证轨迹规划可行性,完成对机器人轨迹的优化设计。机器人示教模型如图3所示。

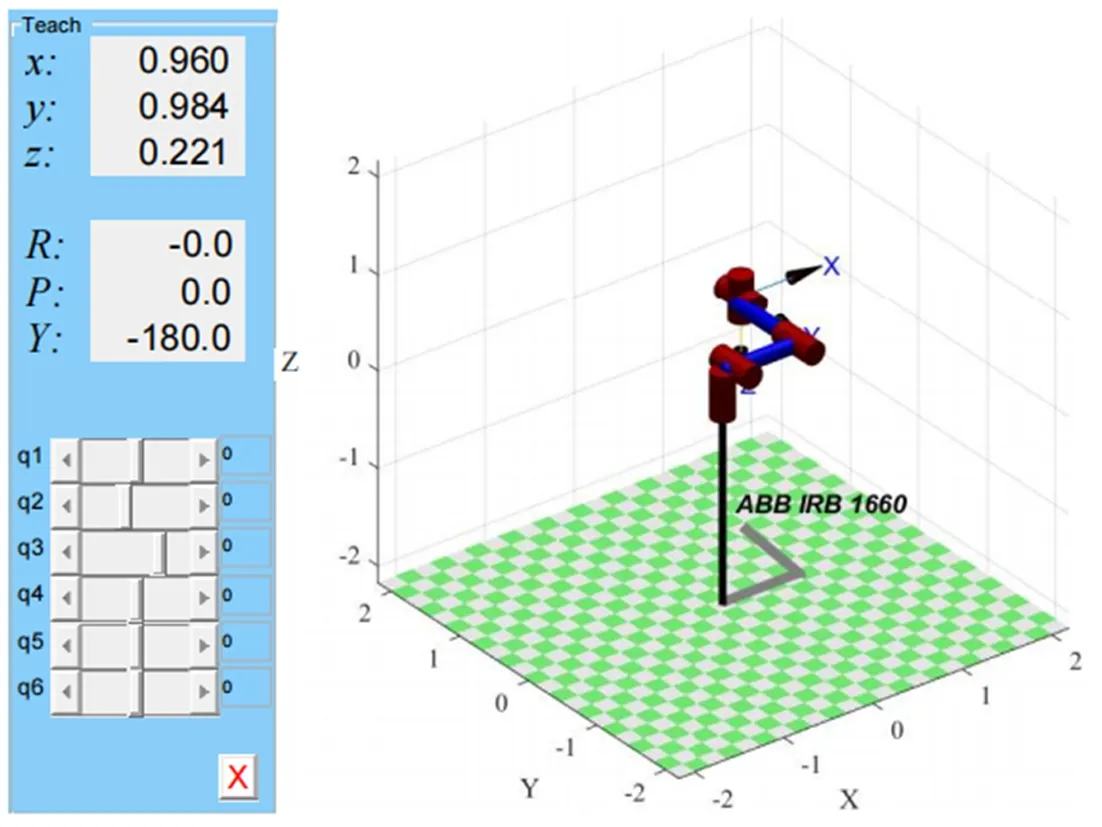
图3 ABB IRB1660机器人示教模型

为了保证机器人作业过程平稳运行且满足运动学约束条件。关节空间中一般采用三次或五次多项式插值,三次插值多项式中加速度存在突变,使得机器人磨损加剧,从而降低工作精度并增加能量消耗;五次插值多项式中加速度虽无突变避免了冲击与振动,但其计算量相对较大且对不同轨迹设计时可能会存在龙格现象,造成电机驱动系统破坏的缺点。而3-5-3多项式兼顾两者优点,在多轨迹点规划中有很强的优势,因而被广泛应用。其具体方法为将路径分为三段进行设计,即0→ta、ta→tb、tb→tf分别进行3次、5次、3次多项式进行插值。

第j关节在0→ta、ta→tb、tb→tf三段的角位移、角速度、角加速度的函数表达式,即:

当0≤t≤ta时,表示为:

(5)

当ta≤t≤tb时,表示为:

(6)

当tb≤t≤tf时,表示为:

(7)

式中,用ti(i=a、b、c)来表示第i关节3段插值多项式的时间,θji表示第j关节4个关节角度点、aj1i、aj2i、aj3i(j=1、2…6;i=0、1、2…5)表示第j关节在任意段路径中插值多项式的系数。

通过上式计算可得插值多项式系数,其表示关系为:

(8)

(9)

(10)

从上述分析可以看出,分段插值多项式系数受到各段时间t的影响,针对t合理取值可达到理想效果。

3 粒子群算法

3.1 传统粒子群算法

粒子群算法的总体思想是针对鸟类群体行为的建模与仿真,提出的一种优化算法。通过种群中信息的交流来驱动种群在空间内不断搜索最优解。首次生成包含n个粒子的初始种群X=(X1、X2、…Xn),每个粒子Xi表示其对应的一个解向量,每个粒子有一个表示其速度向量的Vi来决定其运动的方向和距离,并且根据粒子本身最优位置和种群最优位置更新其变化速度。基于粒子速度来更新粒子的位置用以寻找最优解。粒子的位置和速度随着算法迭代按照式(11)进行更新。

(11)

(12)

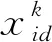
fitness=tj1+tj2+tj3

(13)

(14)

式中,Vjmax、Ajmax分别为机器人各关节运动过程中允许的最大速度、加速度。

3.2 改进粒子群算法

传统粒子群算法中各参数固定不变,易陷入局部最优且后期收敛速度慢等问题。为优化其性能,平衡全局和局部搜索能力。针对ω在线性递减惯性权重的基础上,创新性地提出对其进行非线性处理,对[(ωmax-ωmin)/Nmax]项进行平方处理,相较于传统的线性递减惯性权重,可更好地让其值在搜索前期保持较大值,以此保证各个粒子在搜索空间内充分飞行,后期保持较小值,充分保证各粒子间信息交流学习;c1、c2设置为非线性的动态函数,c1表示个体最大飞行步长,前期其值应较大,c2表示全局最大飞行步长,后期其值应较大。改进后的ω、c1、c2分别见式(15)和式(16)。

(15)

(16)

式中,ωmax表示惯性权重最大值;ωmin表示惯性权重最小值;Nmax表示最大迭代次数;cmax、cmin分别表示表示学习因子最大值、最小值。

改进后的时间最优轨迹规划流程图如图4所示。

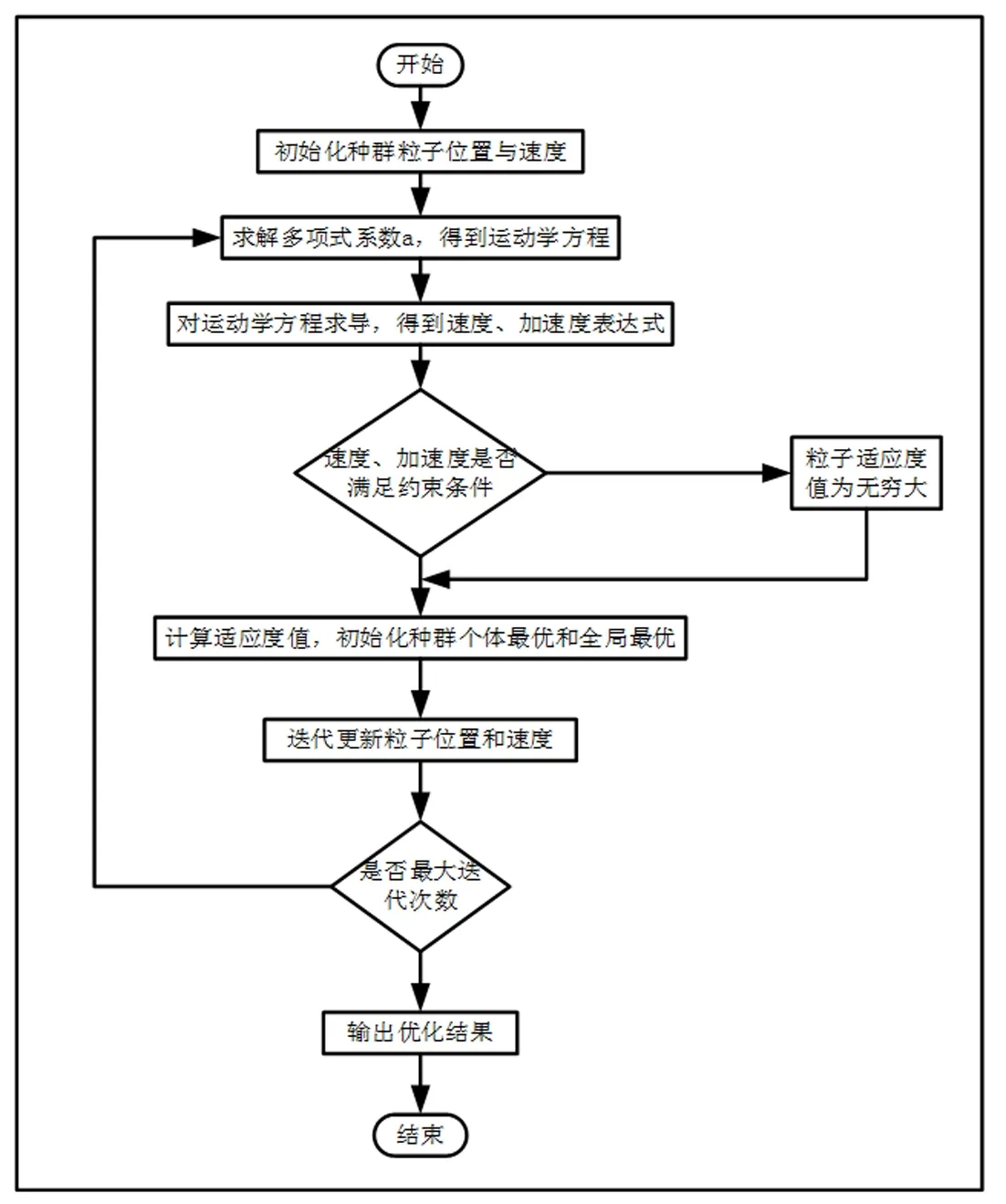
图4 改进粒子群算法优化流程图

4 仿真实验与结果分析

以改进粒子群算法为基础,结合3-5-3插值多项式对机器人轨迹优化方法的正确性和有效性进行验证。采用MATLAB R2022a进行仿真实验研究。各关节在各个轨迹点角度见表2,机器人运动轨迹见图5。

表2 关节角度插值点/°

图5 机器人运动轨迹

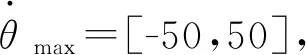
由于机器人3个腕关节(关节4、5、6)轴相交于一点。按照Pieper准则,腕关节只改变机器人姿态,对其位置不产生影响。故以前三关节为主要研究对象得出结果,将传统粒子群算法与优化后粒子群算法进行对比研究。

前三关节经过传统粒子群算法与改进粒子群算法优化后,其适应度值曲线如图6所示。各关节总用时均不同程度少于传统粒子群算法,对机器人效率的提升具有重要意义。另外,在搜索前期粒子群体能够很快地到达全局最优,并且在搜索后期相较于传统粒子群算法可更快地到达局部最优。

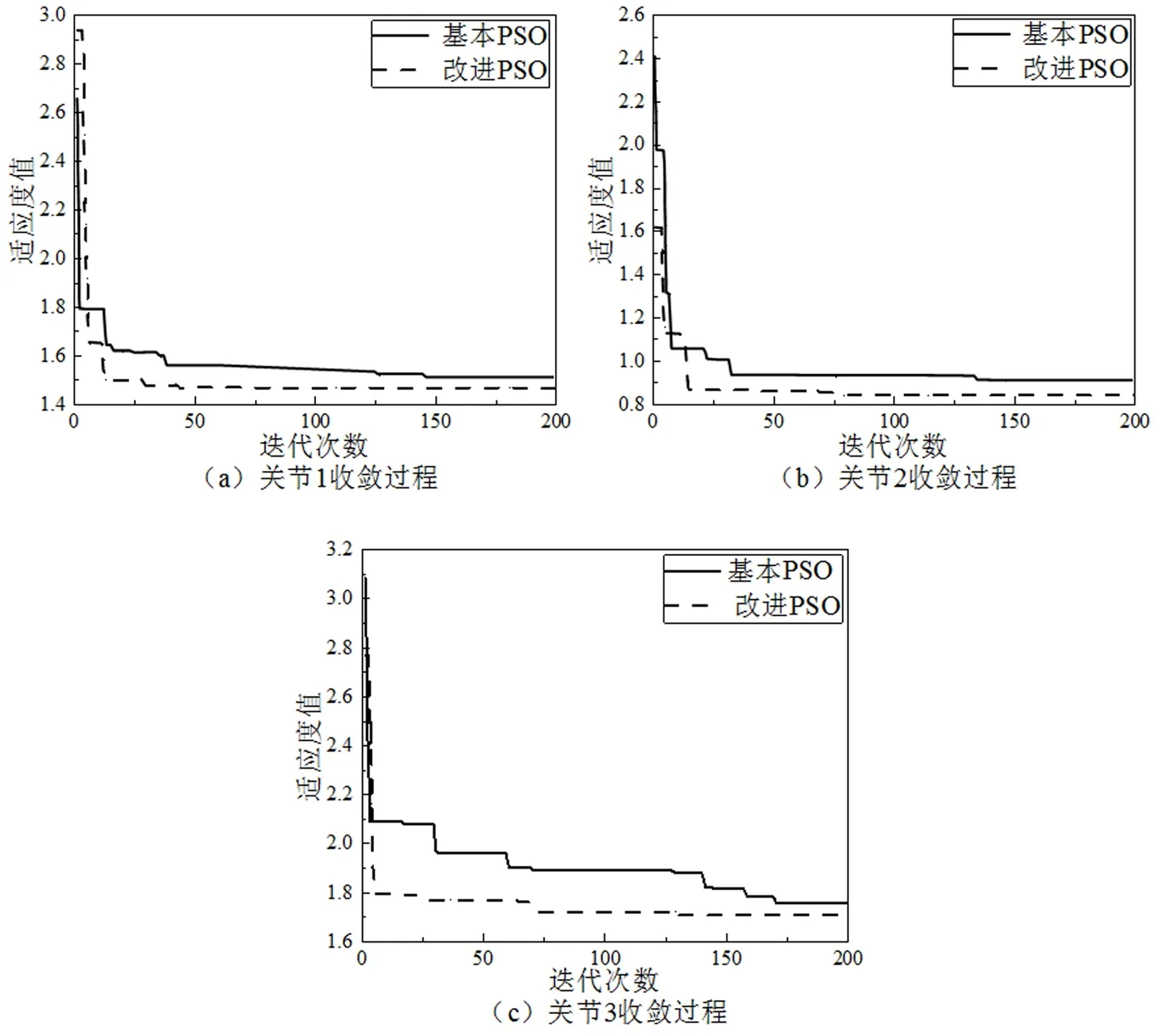
图6 前三关节优化前后适应度值迭代曲线

为确保6R焊接机器人各关节能够稳定、高效地完成既定作业轨迹,设定该轨迹起始点及终止点的加速度、角加速度均为0,且其中间衔接点处的角速度、角加速度均相等。机器人仿真实验优化后时间分量见表3,优化前后各关节位置、速度及加速度曲线对比见图7。

表3 优化后各关节时间分量

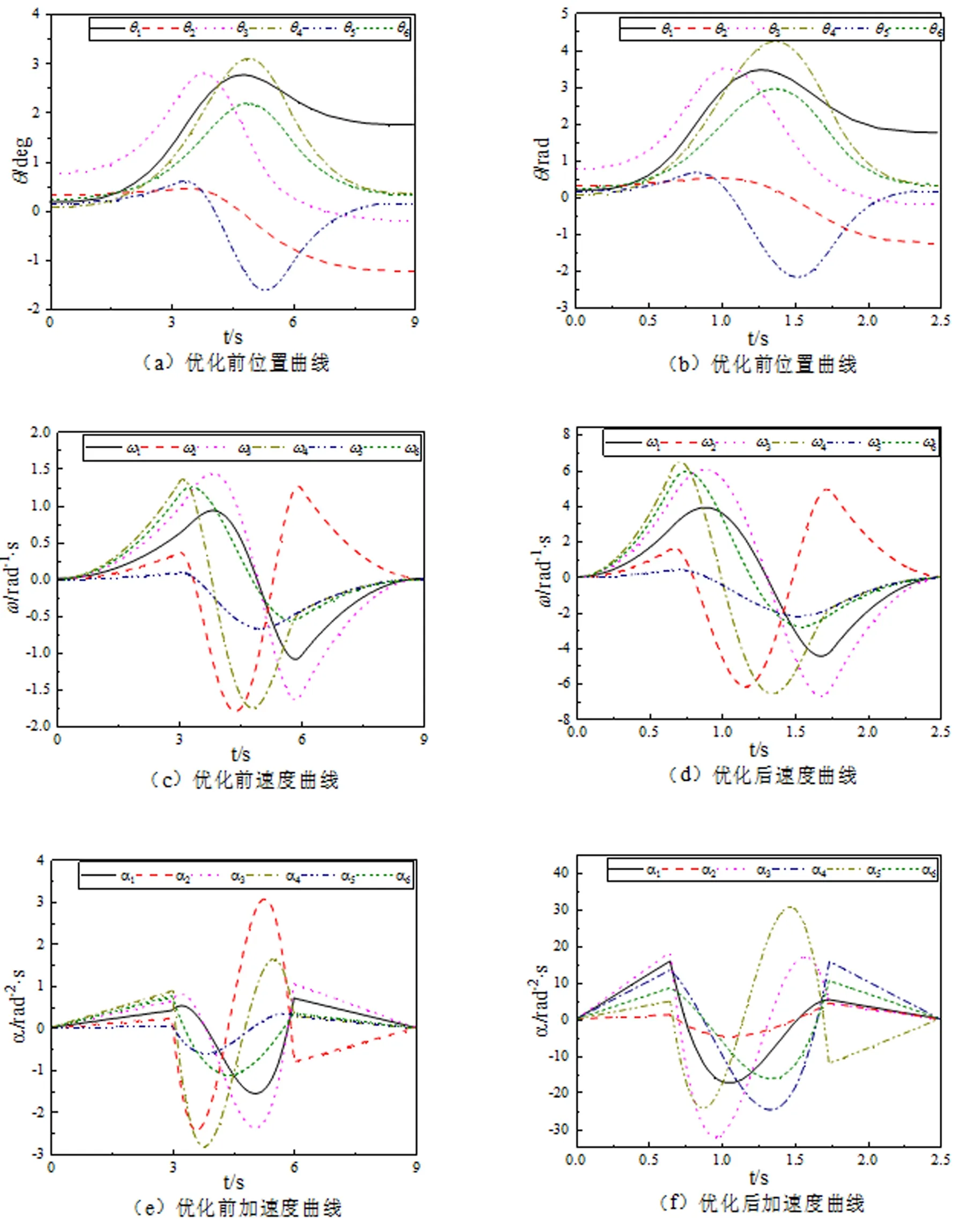
图7 改进粒子群算法优化前后各关节位置、速度、加速度曲线图

由图7机器人分析可知,各关节的位置、速度、加速度曲线更为顺滑且耗时更短。为保证各关节在每段路径中有充足时间完成其相应轨迹且满足关节运动在过程中的运动约束,选取6个关节在各分段轨迹中所用时间最大值。经过该算法优化后完成该段轨迹所需时间由9 s降低至2.49 s,极大地提高了该型号机器人生产效率,有效保证了机器人在高速运动过程中的稳定性。

5 结论

(1)提出一种改进粒子群算法结合3-5-3插值多项式方法来进行轨迹规划,以解决机器人各关节在作业中存在的位置、速度、加速度突变导致运行过程中不稳定而导致机器人磨损加剧、工作寿命降低的问题。

(2)通过采用优化后的递减惯性权重和非线性动态学习因子的方法,在满足机器人运动学约束的条件下,针对机器人轨迹以时间最优为目标进行优化。MATLAB仿真实验得出,该方法在保证了各关节角速度、角加速度曲线平滑的情况下,使得机械人轨迹运行时间极大降低,使得生产效率大幅度提高。因此验证该算法的有效性且相较于其它算法更易于实现,并为其他机器人轨迹优化问题提供借鉴。