基于 PB 试验结合 BBD 响应面法的矿井提升直驱永磁同步电动机设计及优化
2023-10-27黄良沛罗志朋胡志豪李卓军
黄良沛,蒋 浪,罗志朋,胡志豪,李卓军
1湖南科技大学机电工程学院 湖南湘潭 411201
2湖南科技大学机械设备健康维护湖南省重点实验室 湖南湘潭 411201
3湖南煤矿机械有限公司 湖南娄底 417000
提 升机作为矿山采掘和运输场合的重要辅助设备,在矿山竖井或斜井中被大量而广泛地运用于物品与人员的调度,具有较大的牵引功率和很好的安全性,是矿山生产中不可缺少的设备之一[1-2]。提升驱动系统是矿井提升机的核心部分,其可靠稳定的运转是煤炭开采正常运行的关键;然而,目前传统的异步电动机-多级减速机结构的驱动系统结构复杂,整体效率较低,已不能满足目前矿井发展的需要[3]。低速大转矩直驱系统作为传统异步电动机-减速机驱动系统的换代产品,已成为该技术领域的发展方向[4]。低速大转矩永磁同步电动机是实现矿井提升直驱的关键技术之一[5],高性能钕铁硼永磁材料的出现及其性能的日益提高,也为低速大转矩永磁同步电动机的设计、制造和应用创造了良好的条件[6]。将永磁同步电动机引入到矿井提升系统中,对系统性能多个方面将有改善和提高的作用,是未来发展趋势,其应用与发展前景广阔[7]。
对低速大转矩永磁电动机进行设计时,需要根据设计目标来进行优化设计[8]。目前永磁同步电动机的优化设计方法主要有遗传算法、神经网络法、田口法和响应面法等[9]。Bu J G 等人[10]基于最大投影 (Max Pro) 设计了自适应 Kriging 模型 (AKMMP),并建立了采用带精英策略的非支配排序遗传算法 (NSGA-2)和 AKMMP 优化飞轮电动机质量与转矩密度作为考虑转动惯量的性能参数的设计方法。Yu Y Q 等人[11]提出了一种基于响应面法 (RSM) 和非支配排序遗传算法Ⅱ(NSGA-II) 的局部优化寻优方法 (RSM+NSGA-Ⅱ-LR),以降低永磁同步电动机 (SPMSM) 的齿槽转矩。Mohammadi M.H.等人[12]利用神经网络算法搭建电动机模型,对永磁电动机非导磁部分进行优化,实现了电动机的局部尺寸优化。Deepayan G.等人[13]采用正交试验的 Taguchi 法,对永磁同步电动机中永磁体的相关尺寸及位置参数进行优化分析,实现对永磁同步电动机的线电流、负载转矩和效率等性能的优化。杜晓彬等人[14]应用基于中心组合设计 (CCD) 的方法,对响应面模型函数拟合回归求得最优参数解,结果表明:基于响应面法 (RSM) 的优化方法,能有效抑制转矩波动,提高输出转矩和起动转矩的幅值。田口法与响应面法属于局部优化算法,虽然优化精度不如全局优化法,也不能像 NSGA 等遗传算法一样选择较多的优化目标,但其操作步骤简单,收敛速度快,在实际工业电动机中具有很好的实用性[15]。
本研究设计了一套低速大转矩永磁同步电动机,并使用优化设计方法,利用 Plackett-Burman 试验设计结合 Box-Behnken 响应面[16],以齿槽转矩、电磁转矩与转矩脉动为优化目标,对电动机尺寸参数进行优化,并进行电磁对比分析,验证电动机优化设计的合理性。本研究的目的在于开展矿井提升直驱永磁同步电动机设计及优化研究,为矿山直驱电动设计及工程化应用提供理论依据。
1 矿井提升直驱永磁同步电动机设计
本研究设计的低速大转矩永磁同步电动机应用于矿场工作环境,可用于深度为 270 m 矿井运输。该电动机设计为 60 极 54 槽,额定功率为 180 kW,额定转矩为 42.97 kN·m,额定转速为 40 r/min,额定效率为 85%,绝缘等级为 H,额定电压为 660 V。
矿用低速大转矩永磁电动机电磁设计主要包括转子磁路设计、电动机主要尺寸设计、定子冲片设计、绕组设计、永磁体尺寸设计及材料选型[17-19]。
1.1 转子磁路设计
考虑到提升工况要求电动机的运行转速很低,电动机的调速范围不大,本设计选用表面凸出式的转子磁路结构,径向充磁。表面凸出式转子磁路结构的电动机表现出隐极特性,具备结构简单、制造成本低等优点[20]。在极弧系数不变的情况下,电动机的极对数越大,电动机的气隙磁密波形的正弦性越好;但是由于定子内径的限制,极对数不能取的过大,本设计取30 对极。
1.2 电动机主要尺寸设计
永磁同步电动机的主要尺寸是指定子内径Dil和定子铁芯有效长度Lef,可由式 (1) 求得。
式中:Dil为定子内径,cm;Lef为定子铁芯有效长度,cm;Temmax为性能要求最大转矩,N·m;A为线负荷,A/cm;Bδ为气隙磁密基波的幅值,T。
根据矿井直驱永磁同步电动机的设计要求,最大输出转矩
式中:Pn为额定功率,kW;ω为角速度,rad/s。
定子铁心计算长度与定子内径满足下式:
式中:λ为长径比。低速大转矩电动机的长径比一般较小,电动机呈饼状,根据经验选取可初步得到Dil。
气隙长度
式中:δ为气隙长度,m;li为单节铁心长度,m。
1.3 定子冲片设计
因 DW135 系列硅钢片具有磁导率高、低损耗与良好的加工性能,定子材料采用 DW315-50 硅钢片。采用分数槽集中绕组,能够改善永磁电动机的气隙磁场波形,使电动机空载反电势波形的正弦性增加,降低齿槽转矩的大小,有效提高电动机的运行稳定性,故定子槽取 54 槽。为了使定子齿部磁密均匀分布,避免齿部的局部饱和,故齿槽形状采用梨形槽,如图1 所示。在满足正常工作状况下的机械强度,并且考虑到定子磁密的幅值大小,在基于下线顺利的前提下,适当减小定子齿部与轭部宽度,最终槽口宽Bs0=12 mm,槽口高度Hs0=3 mm。此外,为了保证定子铁心具有足够的强度和较低的附加损耗,Hsl=5 mm,Hs2=60 mm,Bsl=44 mm,Bs2=50 mm。

图1 定子槽的尺寸Fig.1 Size of stator slot
1.4 绕组设计
为降低电动机损耗与谐波含量,使电动机的感应电动势波形更接近正弦,本设计采用了分数槽集中绕组,双层绕组。每槽绕组匝数对电动机的输出性能有很大的影响,根据预取的线负荷A,电动机的每相串联绕组匝数
式中:p为永磁体极对数;τ1为定子极距;m为输入电流的相数;IN为额定电流;Kdp为绕组的分布系数,根据所选的极槽配合及绕组跨距,Kdp为 0.933。则每层每槽导体数
式中:a为最大并联支路数;Z为定子槽数。
1.5 永磁体尺寸设计
对于本设计所选择表面凸出式子磁路结构的永磁电动机,永磁体轴向长度与电动机定子铁芯长度相同,永磁体的磁化方向长度及宽度可由下式确定:
式中:hm为永磁体磁化方向长度;bm为永磁体宽度;mm;ur为相对回复磁导率;Br为永磁体剩磁密度,T,Br/Bδ一般取值 1.10~ 1.35。
2 齿槽转矩产生原理与分析
2.1 齿槽转矩产生原理
齿槽转矩的产生是由电动机自身结构所导致。当电动机转动时,其转子上永磁体极弧部分与其对应的定子电枢齿间的磁导强度基本不变,这些电枢齿附近的磁场也基本不变;但是由于定子齿槽的存在,与永磁体两个侧面即将靠近或远离的定子齿所在的区域内,磁导产生较大的变化,故引起磁场储存能量的变化 (见图2),磁场为了稳定所带来的牵引力,从而产生了齿槽转矩。齿槽转矩会给电动机运行过程中带来输出转矩的波动,会导致振动和噪声的产生,因此在设计过程中必须对参数进行优化设计,使齿槽转矩达到设计要求范围内,实现系统运行的稳定性。

图2 齿槽转矩的产生Fig.2 Generation of cogging torque
2.2 齿槽转矩的分析
由齿槽转矩的产生原理分析可知,齿槽转矩可以定义为绕组不通电时,电动机转动所带来的磁场能量变化,表示为
式中:W为磁共能;a为永磁体与定子齿中心线间的夹角。
式 (8) 经过一系列假设推导,最终可得齿槽转矩表达式为
式中:R1为转子外半径;R2为定子内半径;Z为定子槽数;P为极对数;n为使得nZ/2P为整数的整数;u0为空气磁导率;θ s0为用弧度表示的电枢槽口宽;aP为极弧系数。
从式 (9)、(10)、(11) 可以看出,除了电动机主要外形参数尺寸外,齿槽转矩主要由n、Br和GN这3 个参数影响,其中极弧系数、永磁体参数影响着Br的大小;而GN与定子槽尺寸参数、气隙长度有关。因此,本研究主要从极弧系数aP、永磁体磁化方向长度hm、槽口宽度Bs0、槽口高度Hs0与气隙大小δ来进行齿槽转矩的优化设计,并同时考虑电动机的电磁转矩与转矩脉动。
3 参数优化试验设计与分析
基于前面所设计的 60 极 54 槽表贴式 PMSM,使用 Maxwell 软件建立仿真模型,选取极弧系数aP、永磁体磁化方向长度hm、槽口宽度Bs0、槽口高度Hs0与气隙大小δ为优化参数,以齿槽转矩τCog、电磁转矩τr、转矩脉动τripple为分析对象,采用 Plackett-Burman试验法结合 BBD 响应面法进行优化设计,过程如图3 所示。

图3 优化分析流程Fig.3 Optimization analysis flow
3.1 单因素试验分析
在极弧系数aP=0.7、永磁体磁化方向长度hm=12 mm、槽口宽度Bs0=14 mm、槽口高度Hs0=3 mm、气隙长度δ=2 mm 的恒定条件下,分别对各个因素进行考察,在考虑齿槽转矩与转矩脉动较低的同时,使转矩脉动处于一个较高水平,分别选取一个最优值进行后续试验。
3.1.1 极弧系数
极弧系数aP为一个极距下永磁磁极所占有的宽度,而永磁体的宽度直接决定了永磁体能够提供的磁通量,会影响气隙磁场中高次谐波和齿谐波分量的幅值。极弧系数过小,会导致电动机的输出性能降低;而对于表贴式永磁体转子结构,极弧系数越大,极间漏磁会上升,还会增加感应电势谐波分量,引起转矩波动和电动机损耗的增加。
单因素试验选取 0.70~ 0.86,步长为 0.04 的 5 个水平进行有限元仿真分析,其对齿槽转矩、电磁转矩、转矩脉动的影响如图4 所示。
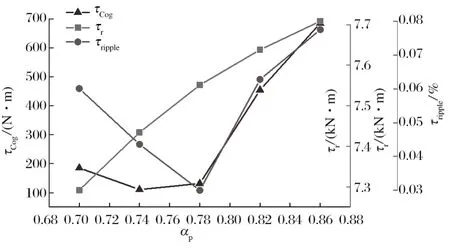
图4 极弧系数对优化目标的影响Fig.4 Influence of polar arc coefficient on optimization object
从图4 可知,随着极弧系数的变大,齿槽转矩与转矩脉动呈先降低然后再急剧增大的过程,而电磁转矩一直呈现一个稳定上升的趋势。考虑综合,选取aP最优值为 0.78。
3.1.2 槽口宽度与槽口高度
槽口宽度Bs0与槽口高度Hs0主要由电动机电气性能、冲模制造、冲压和下线工艺等因素决定[21]。槽口尺寸的变化会对电动机电动势基波幅值与齿部漏磁大小带来影响。在满足电气性能与嵌线方便的前提下,槽口宽度取较小值。取槽口宽度Bs0为 6、8、10、12和 14 mm,槽口高度Hs0为 2、3、4、5 和 6 mm,分别进行单因素试验,结果如图5、6 所示。
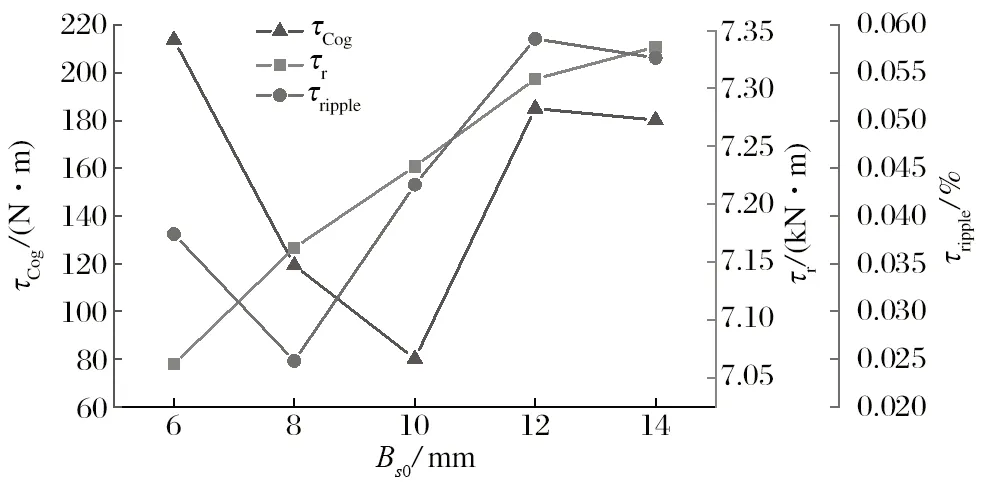
图5 槽口宽度对优化目标的影响Fig.5 Influence of slot width on optimization object
从图5 可以看出:电磁转矩随着槽口宽度的增加一直处于缓慢增加的趋势;而槽口宽度从 6 mm 到 10 mm,齿槽转矩急剧降低,在槽口宽度为 10 mm 时处于一个最低值,然后再上升;转矩脉动也呈现一个先降低再升高的趋势,在槽口宽度为 8 mm 时取得最低值,选取齿槽宽度最优值为 8 mm。由图6 可知,随着槽口高度的增加,齿槽转矩先急剧增加,而后缓慢降低;电磁转矩与转矩脉动缓慢上升,而在槽口高度为 5 mm 时,电磁转矩呈现下降趋势,故选取Hs0最优值为 4 mm。

图6 槽口高度对优化目标的影响Fig.6 Influence of slot height on optimization object
3.1.3 永磁体磁化方向长度
永磁体磁化方向长度hm影响着电动机的直轴电感,磁化方向长度的增大使得直轴方向磁导减小,进而导致直轴的电感减小,使电动机的“弱磁”调速性能降低,但可以提高电动机转矩的幅值。永磁体磁化方向长度太小,使得电动机的抗去磁能力下降,容易退磁,导致电动机性能不能满足设计要求[22]。对磁化方向长度选取 8~ 16 mm,步长为 2 mm 的 5 个水平进行分析,结果如图7 所示。
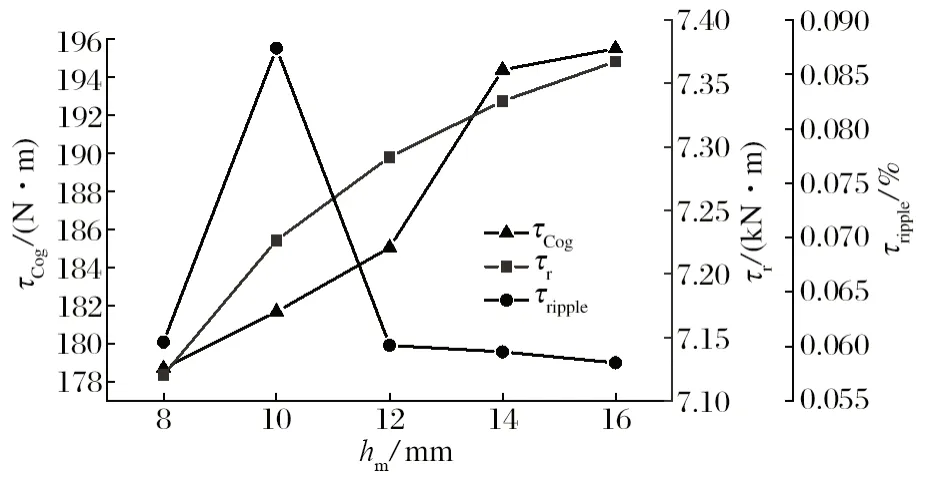
图7 永磁体磁化方向长度对优化目标的影响Fig.7 Influence of magnetization direction length of permanent magnet on optimization object
从图7 可以看出,优化参数的变化,转矩脉动在hm=10 mm 时处于一个极大值,其余位置水平相差不大;电磁转矩处于增加速度逐渐变缓的过程;而齿槽转矩的趋势是快速增加,在hm=14 mm 时增速开始减缓,在hm=16 时为最大值。因而,选取磁化方向长度hm=12 为最优参数进行后续试验。
3.1.4 气隙长度
气隙作为能量交换场所,气隙尺寸δ对电动机性能是一个重要的影响参数。气隙过小,容易导致电动机在运转过程中产生撞击,也会使安装困难,但是气隙较小可以提高电动机的功率因素;气隙较大,可以降低气隙中的谐波幅值,减少杂散损耗[23]。取气隙在1.2、1.4、1.6、1.8 和 2.0 mm 5 个水平下仿真分析,结果如图8 所示。可见,随着气隙长度的增加,3 个优化目标都处于逐渐降低趋势,考虑综合影响,取δ=1.8 mm 作为最优值进行后续试验。
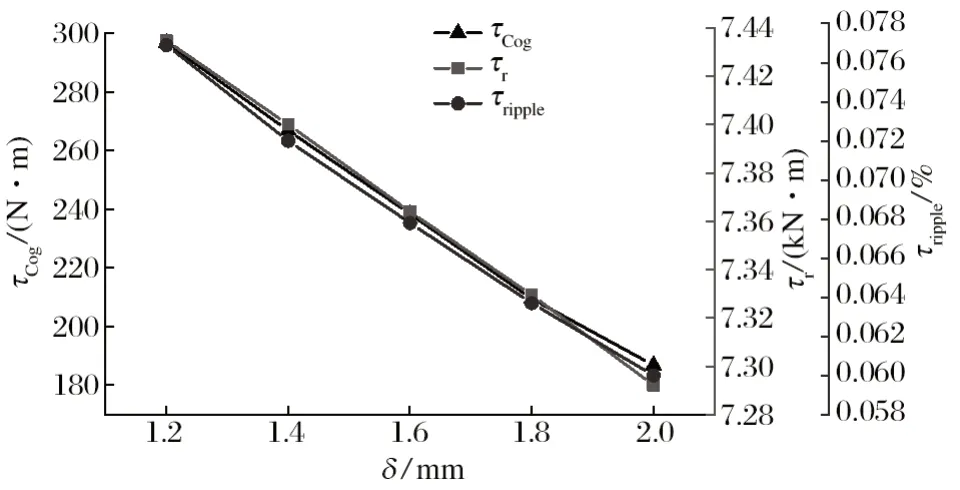
图8 气隙长度对优化目标的影响Fig.8 Influence of air gap length on optimization object
3.2 PB 试验筛选显著性因素
使用 Design-Expert 软件设计 12 次 PB 试验,对槽口宽度Bs0(因素 a)、槽口高度Hs0(因素 b)、极弧系数aP(因素 c)、气隙长度δ(因素 d)、永磁体磁化方向长度hm(因素 e) 进行齿槽转矩、电磁转矩、转矩脉动的显著性考察,每个因素根据前面的单因素试验设计高低两个水平,分别用 1、-1 表示。各因素水平如表1 所列,试验结果如表2 所列,模型方差分析如表3~ 5 所列。
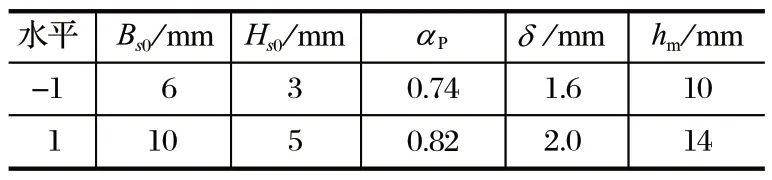
表1 PB 试验因素水平Tab.1 PB test factor levels
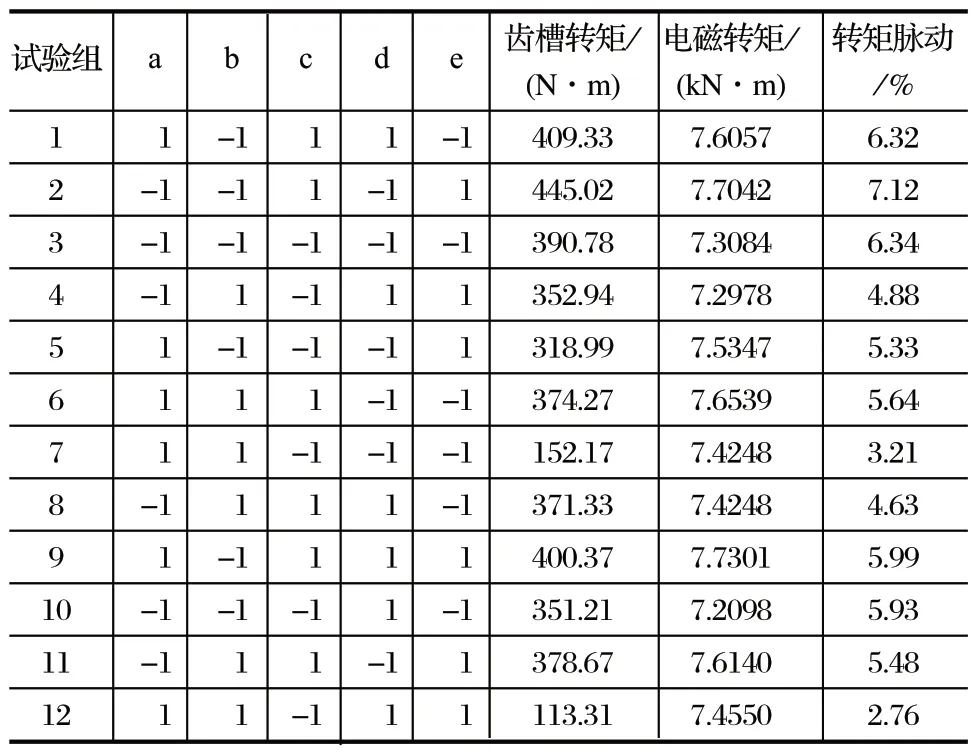
表2 PB 试验方案与结果Tab.2 PB test scheme and results
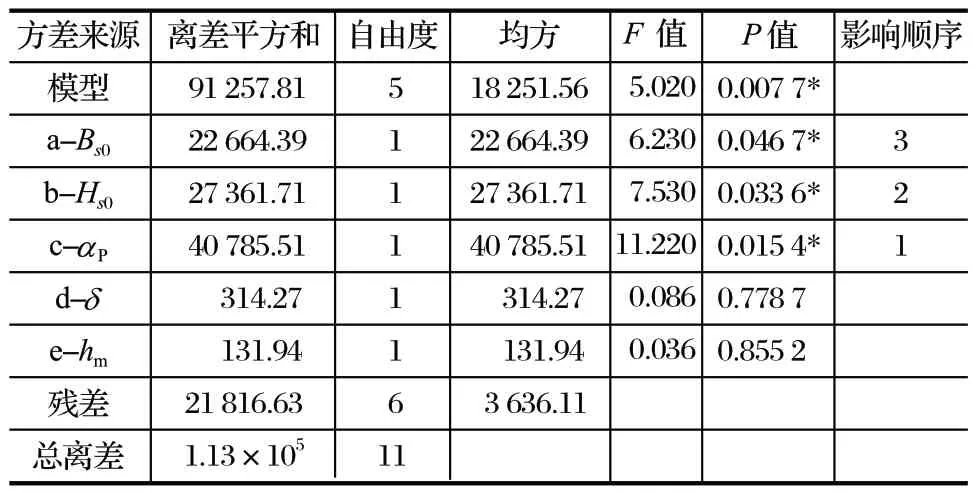
表3 PB 试验齿槽转矩方差分析结果Tab.3 Results of variance analysis of cogging torque in PB test
表3、4、5 分别表示 5 个因素对齿槽转矩、电磁转矩、转矩脉动的回归方程系数及显著性检验结果。由回归模型的方差分析结果可知,3 个回归模型的P值均小于 0.001,回归模型较显著;其中,电磁转矩的回归模型的P值小于 0.000 1,回归模型高度显著,满足试验可行性要求。从表3 的P值大小可以看出槽口宽度、槽口高度与极弧系数对齿槽转矩的影响显著性,显著性大小排序为 c > b > a。表4 表明槽口宽度、极弧系数、永磁体磁化方向与对电磁转矩的影响极其显著,而槽口高度的影响最显著,大小排序为 a> c > e > d > b;同样从表5 可以看出,对转矩脉动的显著影响因素大小排序为 b > c > a。综上所述,考虑对 3 个优化目标影响都显著的三因素进行后续 BBD响应面试验分析,故选取槽口宽度、槽口高度与极弧系数三因素为建立 BBD 响应面的考察目标。

表4 PB 试验电磁转矩方差分析结果Tab.4 Results of variance analysis of electromagnetic torque in PB test
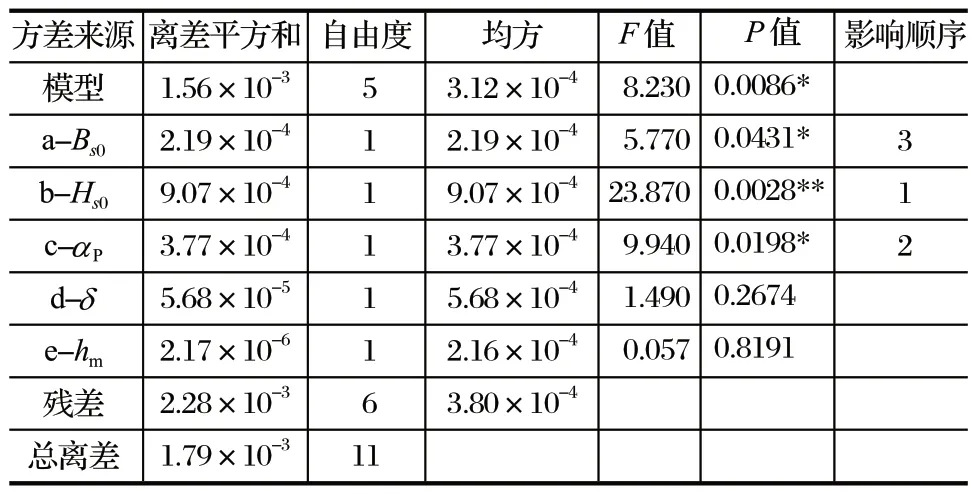
表5 PB 试验转矩脉动方差分析结果Tab.5 Results of variance analysis of torque ripple in PB test
3.3 BBD 响应面试验优化分析
3.3.1 BBD 响应面试验设计
基于单因素试验与 PB 试验结果,选取槽口宽度、槽口高度、极弧系数作为响应面模型设计的考察变量,以齿槽转矩、电磁转矩、转矩脉动为指标进行响应面分析。使用 Design-Expert 软件,每个因素都设计高、中、低 3 个水平分别用 1、0、-1 表示,因素水平如表6 所列。共设计 17 个试验组,在永磁体磁化方向为 12 mm、气隙长度为 1.8 mm 的条件下完成所有试验组,方案设计与结果如表7 所列。
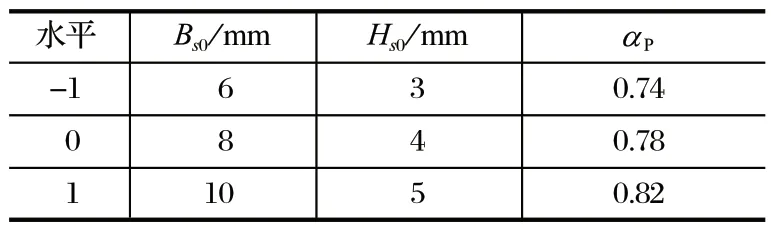
表6 BBD 响应面试验因素水平Tab.6 BBD response surface test factor levels

表7 BBD 响应面试验方案与结果Tab.7 BBD response surface test scheme and results
3.3.2 BBD 响应面试验方差分析
使用 Design-Expert 软件进行软件对试验结果进行方差分析,分别对齿槽转矩、电磁转矩与转矩脉动进行多元回归拟合方程分析,回归方程分别为:
回归模型的方差分析结果如表8~ 10 所列。3 个模型的P<0.05,说明方程线性拟合度高;失拟项的P> 0.05,不显著,说明未知因素对试验的影响小;3 个模型的R2均大于 90%,表明模型可以解释各优化目标的变化。由表8~ 10 可知,方程中的一次项 a、b、c 对优化目标的评分P< 0.05,影响显著;而 a2、b2、c2的P< 0.001,对优化目标的影响较显著,说明各因素对优化目标的影响呈二次线性关系。
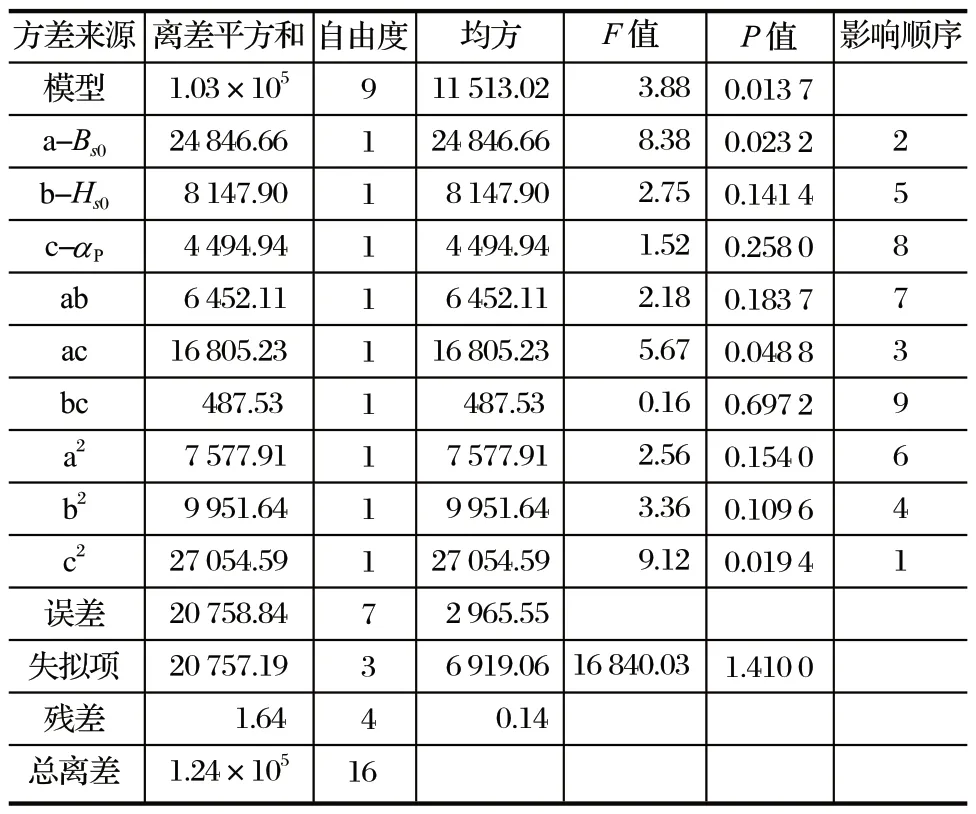
表8 齿槽转矩回归模型方差分析Tab.8 Variance analysis of cogging torque regression model
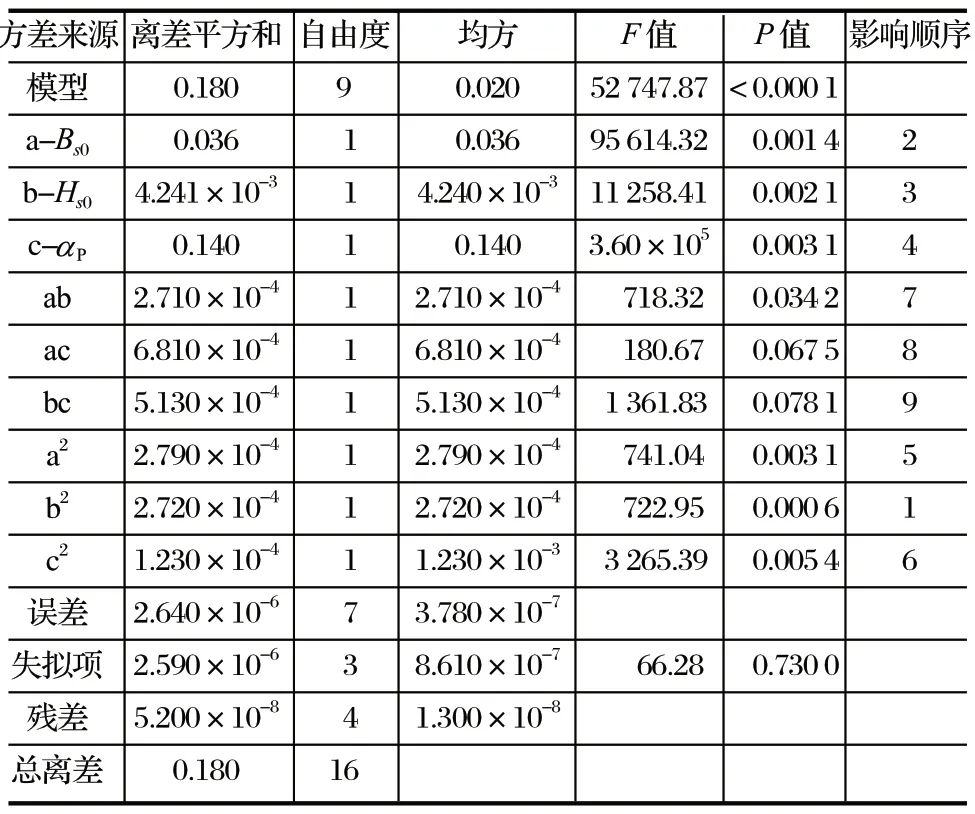
表9 电磁转矩回归模型方差分析Tab.9 Variance analysis of electromagnetic torque regression model
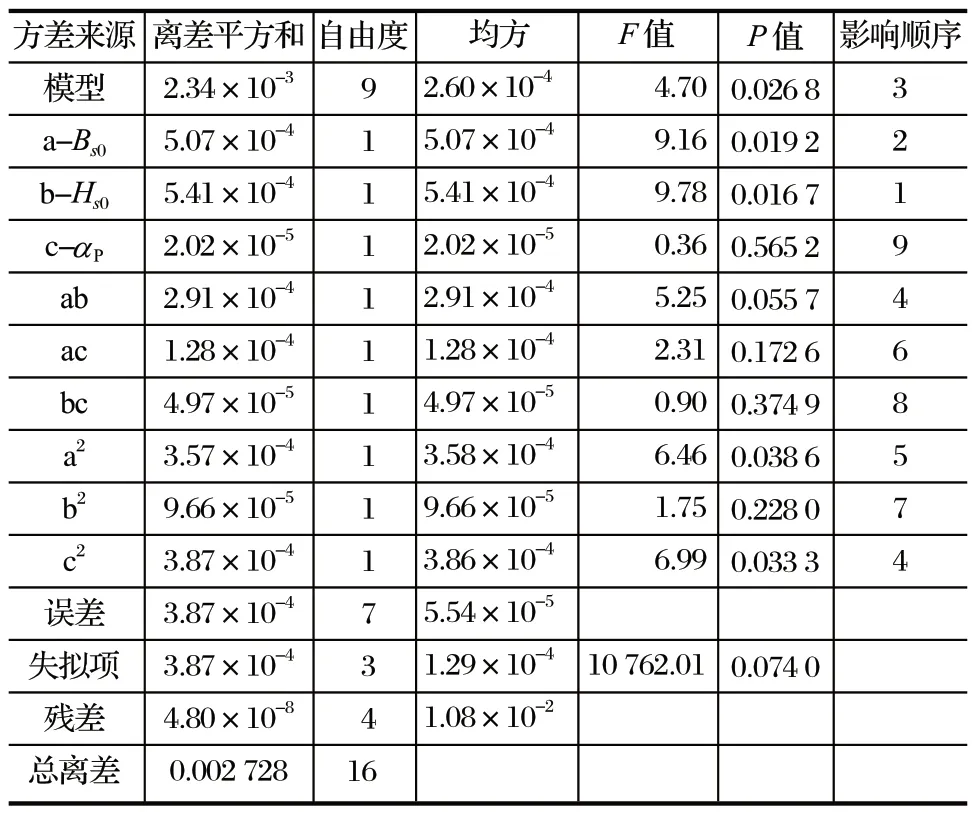
表10 转矩脉动回归模型方差分析Tab.10 Variance analysis of torque ripple regression mode
3.3.3 响应面因素间的交互作用分析
利用软件 Design-Expert,根据拟合模型绘制交互影响三维曲线图,分析各因素的交互作用对优化参数的影响。由图9 可以看出,当因素 a 保持一定水平时,随着因素 b 的增加,齿槽转矩处于一个平缓的先增加后减少的趋势,曲面变化也较为平缓,说明 a、b两因素的交互作用对模型无显著影响;当因素 a 保持一定水平,随着因素 c 的变化,齿槽转矩处于一个较大的波动,曲面的波动也比较大,与模型分析的结果一致,a、c 的交互作用对齿槽转矩有着显著影响;当因素 b 水平保持一定时,随着因素 c 的变化,齿槽转矩处于一个先减少后增加的平缓趋势,曲面平缓,表明 b、c 的交互无显著影响。同理,根据图10、11 分析 a、b、c 三因素的交互作用对电磁转矩与转矩脉动的影响,与方差分析的结果一致。
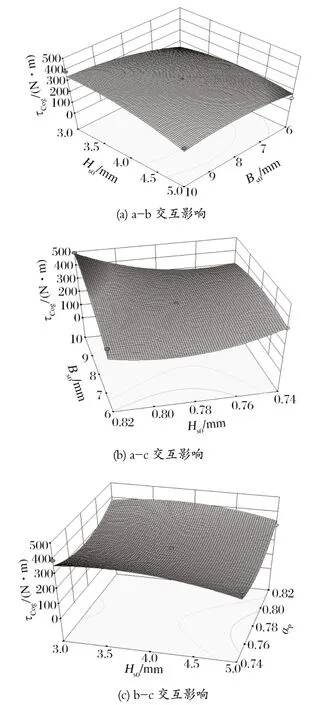
图9 a、b、c 两两交互对齿槽转矩影响的三维效应面Fig.9 Three-dimensional effect surfaces of interaction between a,b and c on cogging torque
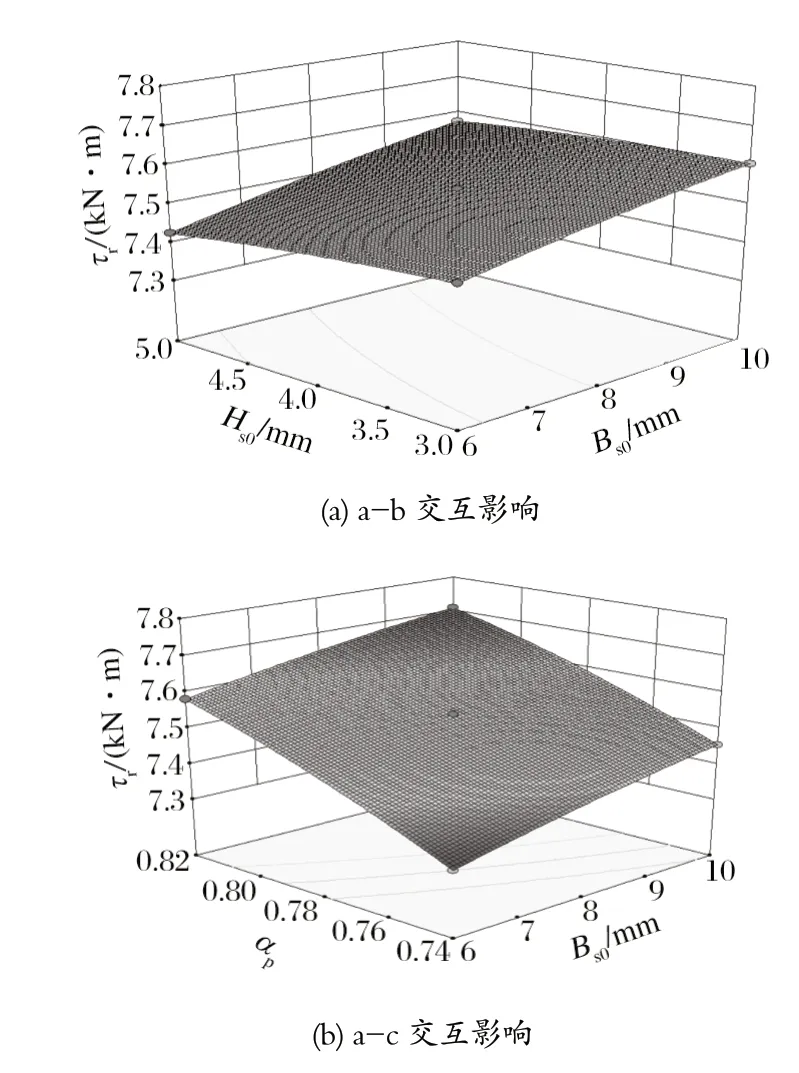
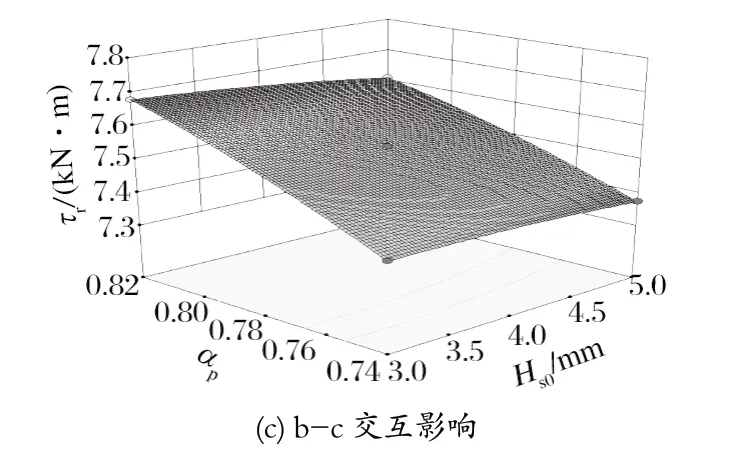
图10 a、b、c 两两交互对电磁转矩影响的三维效应面Fig.10 Three-dimensional effect surfaces of interaction between a,b and c on electromagnetic torque

图11 a、b、c 两两交互对转矩脉动影响的三维效应面Fig.11 Three-dimensional effect surfaces of interaction between a,b and c on torque ripple
使用 Design-Expert 软件分析得出:在齿槽转矩与转矩脉动相对较低、电磁转矩不低于要求的最佳优化参数为Bs0=5.8 mm,Hs0=4.7 mm,aP=0.778。考虑加工方便,Bs0取 6 mm,Hs0取 4.5 mm,aP取 0.78。
3.3.4 优化前后电动机性能
基于优化前设计参数与优化后的最优参数进行仿真分析,优化前与优化后电动机性能如表11 所列。

表11 优化前后电动机尺寸参数与性能Tab.11 Motor size parameters and performance before and after optimization
4 有限元电磁仿真分析
使用 Maxwell 的 RMxprt 模块根据所设计的电动机参数建立电动机分析模型,使用 Maxwell2D 模块进一步划分网格、设置运行参数,进行电磁仿真分析。由于电动机结构对称性,采用 1/6 模型分析以降低仿真计算时间,仿真模型如图12 所示。

图12 电动机 1/6 模型的网格剖分Fig.12 Grid generation of 1/6 motor model
基于 Maxwell2D 所搭建的仿真模型,对所设计的电动机分别进行有限元空载与负载仿真分析,求解空载与负载状态下不同时刻的磁密云图与磁力线分布,结果如图13~ 16 所示,并得到电动机优化前后的电磁转矩与齿槽转矩波形图,如图17、18 所示。
由图13 可知:在负载下,定子齿磁密平均值约为 1.5 T,定子轭部磁密的平均值约为 0.85 T;磁密最高点出现在定子的齿尖部分,最大值约为 2.35 T。由图15 可知,空载情况下,定子齿部磁密的平均值约为 1.45 T,定子轭部磁密的平均值约为 0.68 T;磁密最高点依旧为定子的齿尖部分,最大值约为 2.20 T,符合电动机设计要求。从图14、16 可以看出,磁力线分布均匀,呈对称分布的状态,少量漏磁产生在永磁体间属于正常现象,各条磁力线基本都垂直穿过气隙部分,形成一个个闭合的磁路,进一步验证了电动机设计的合理性。

图14 负载下电动机不同时刻磁力线分布Fig.14 Distribution of magnetic lines of motor at different times under load condition
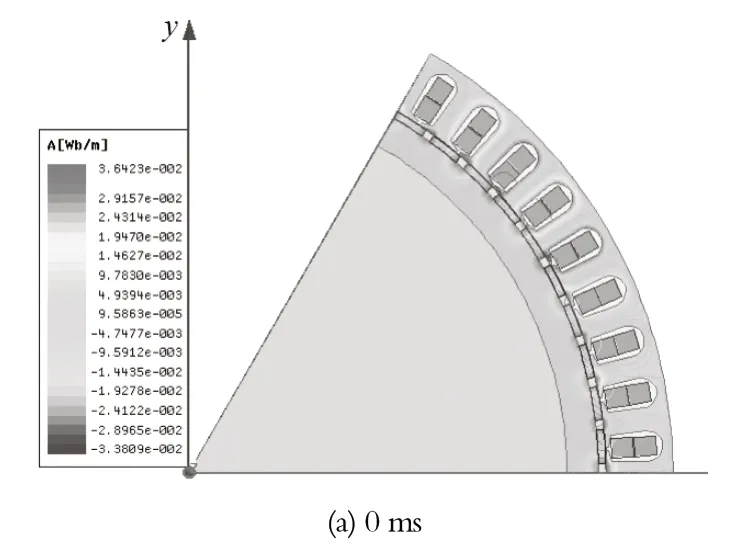
图16 空载下电动机不同时刻磁力线分布图Fig.16 Distribution of magnetic lines of motor at different times under no-load condition
由于有限元仿真分析的是 1/6 模型,所得电磁转矩的 6 倍才是电动机的额定负载转矩。由图17 可知,所设计电动机的电磁转矩为 44.67 kN·m,波动范围在 43.41~ 45.48 kN·m,满足提升所需的转矩值,符合设计要求。
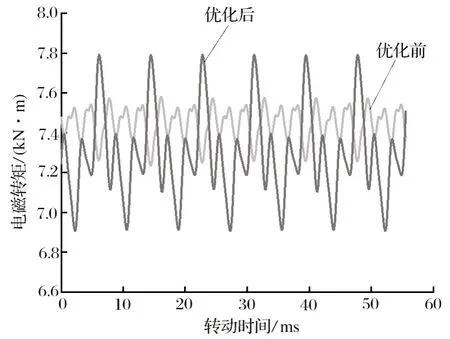
图17 优化前、后电磁转矩波形Fig.17 Electromagnetic torque waveforms before and after optimization
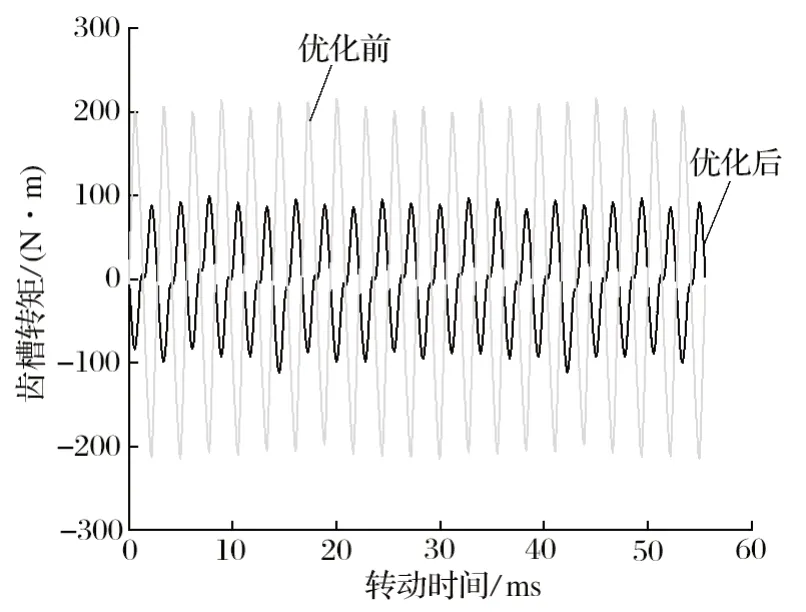
图18 优化前、后齿槽转矩波形Fig.18 Cogging torque waveforms before and after optimization
5 结论
(1) 通过对电动机磁路、主要结构尺寸和冲片结构的分析,所研发的永磁同步电动机能够满足矿井提升的工作需求。
(2) 采用 Plackett-Burman 试验结合 Box-Behnken响应面法进行电磁优化,有效地提高了电动机的电磁性能,齿槽转矩下降了 48.27%,电磁转矩提升了2.2%,转矩波动下降了 3.68%。
(3) 通过电动机在空载与负载下电磁仿真对比分析,进一步验证了所设计电动机的合理性,可为矿井提升机的发展提供相应的技术支持。
