Fe-Mo-Nb合金中溶质拖曳晶粒长大动力学的相场模拟

2023-10-27陈宇鹏王庆宇

原子能科学技术 2023年10期

程刚,陈宇鹏,王庆宇

(哈尔滨工程大学核科学与技术学院,黑龙江哈尔滨 150001)

铁铬铝合金具有优异的抗高温氧化性能,作为耐热材料在工业上广泛应用,同时也是轻水堆(LWR)事故容错燃料(ATF)包壳候选材料[1]。

为进一步提高铁铬铝合金的性能,研究人员在合金中添加各类微量元素,以影响合金微观结构的演变,进一步提升合金宏观性能。其中Mo、Nb广泛应用于炼钢工业,实现材料微观结构和机械性能的调节。已有实验[2]观察到,微量Mo、Nb添加对铁铬铝晶粒细化和热稳定的提高有益,其潜在机制是第二相析出和溶质拖曳对晶界迁移动力学的延迟效应[3]。第二相钉扎和溶质拖曳存在竞争关系,但两者具体以何种方式共同作用是一个复杂的过程,至今尚不明确。

溶质拖曳效应(SDE)是溶质原子与运动晶界之间相互作用的结果,目前主流的溶质拖曳理论有两种:一是Cahn[4]提出的力理论,假设溶质原子和晶界之间存在相互作用能,溶质阻力等于整个晶界范围内溶质原子向左和向右拉动晶界的净力总和;另一种是Hillert等[5]提出的耗散理论,该理论认为SDE是由于运动晶界处溶度分布偏离平衡,溶质原子扩散导致自由能耗散,这种能量耗散过程消耗了部分局部化学驱动力。同时,Hillert等证明,如果力理论模型中依赖的晶界处结合能与耗散理论模型中晶界处扩散系数在各自方程中起到相同作用,则基于两种物理模型方程计算的结果一致,对运动晶界的影响相同。

有研究结合相场法(PFM)计算SDE,获得了不错的成果。早期,Chen等[6]使用相场方法模拟晶粒生长动力学,研究了溶质偏析对晶界(GB)迁移的影响,但模型缺乏相应的溶质拖曳理论支持。Cha等[7]通过将晶界视为可区分的相,并在晶界区域采用“偏析势”,将溶质阻力纳入模型。Kim等[8]尝试了在更大尺度上模拟溶质在晶界处的偏析,证明相场方法可以定量准确地描述考虑SDE的晶界迁移过程。

本研究拟建立多晶溶质拖曳相场模型,对模型的热力学和动力学性质进行阐明,讨论各相场参数间的联系和取值,推导晶界处溶质分布的表达式和溶质拖曳的作用形式,建立定量模拟模型。然后基于自主开发的相场程序模拟序参量分布,并与推导公式进行比对,验证模型定量分析的可靠性;同时计算稳态情况下溶质和对应耗散能分布,模拟圆形晶粒的晶界迁移,探究Mo和Nb溶质拖曳对晶界迁移的影响。

1 相场模型

为模拟FeMoNb合金晶界迁移过程中溶质的拖曳效应,本工作在Cha相场模型[7]基础上进行适当修改,包括引入多晶相场模型、用拖曳项替换依赖于晶界处溶质浓度的偏析势计算。

1.1 相场模型构建

本工作基于KKS相场模型[9]对含微量Mo和Nb的铁素体合金进行动力学模拟,相较于WBM模型[10],KKS模型体系各项体积自由能对界面能没有影响,故适用于扩大界面演化。模型中基体和晶界被视为两相,本节主要探讨KKS模型的约束条件,系统总吉布斯自由能、局部自由能函数、Fe-Mo-Nb三元合金热力学模型、多晶相场模型。

Fe-Mo-Nb三元合金的总吉布斯自由能表达式如下:

(1)

其中:Vm为体系的摩尔体积分数;f为局部自由能密度函数;cMo和cNb分别为Mo和Nb的摩尔分数;η为序参量;n为η的取向数;κi为梯度能系数。

局部自由能密度函数f的形式为:

f=(1-P(η)fm+P(η)fGB+wg(η)

(2)

其中:fm和fGB分别为基体相和晶界相的吉布斯自由能;P(η)为权重函数,基体相取0,晶界相取1;g(η)为双势阱函数;w为势阱高度,与界面能相关。

基体吉布斯自由能函数fm由Zou等[11]的Fe-Mo-Nb三元合金热力学模型给出,模型基于计算相图方法(CALPHAD)建立,形式如下:

(3)

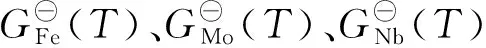
KKS模型中,两相界面是由化学成分不同的两相混合而成,且化学势相等,满足式(4)、(5)的约束条件:

c=(1-P(η))cm+P(η)cGB

(4)

(5)

为满足式(5)的约束条件,晶界相的吉布斯自由能函数fGB可表达为:

(6)

(7)

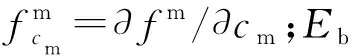
权重函数P(η)和g(η)采用相似的形式:

(8)

P(η)=8g(η)

(9)

其中:α、β、γ为多晶相场系数;B=α/2-β/4。

非守恒相场变量η的时间演变由Allen-Cahn方程[13]获得,守恒相场变量cMo和cNb的时间演变由Cahn-Hilliard扩散方程[14]控制。其形式如下:

(10)

(11)

其中:L为界面迁移率;MC为溶质原子迁移系数。

1.2 平衡系数和相场参数

本节将基于系统平衡状态给出的各类边界条件构建多晶相场模型,推导序参量η、界面厚度2l、界面能σGB的表达式,获得梯度能系数κi、势阱高度w的关系式。

由式(2)、(10)可得:

(12)

(13)

平衡时,∂η/∂t=0,m为常数,只考虑一维情况,结合式(8)、(12)可得:

(14)

式(14)满足以下条件:基体内ηi=1、ηj=0、d2ηi/dx2=0;晶界处ηi+ηj=1;晶界中心ηi=ηj=0.5,d2ηi/dx2=0。将以上条件代入式(14)可得多晶相场系数α=β、γ=1.5α,结合权重函数条件,取向为i的基体内ηi=1、P(ηi)=0;取向为i、j的两晶粒晶界中心(晶界相),ηi=ηj=0.5,P(ηi)=1,可得α=β=1、γ=1.5。式(14)可进一步表示为:

(15)

双势阱函数(式(8))可表示为:

g(η)=

(16)

考虑到取向为i、j的两晶粒晶界处仅ηi、ηj不等于0,结合对称条件ηi+ηj=1,式(16)可化为ηi的表达式:

(17)

要得到序参量的分布式,先对式(15)积分,可得:

(18)

由条件x=±∞,dηi/dx=0,ηi=0或1可得A=0,对式(18)积分得序参量的分布式:

(19)

式(19)提供了平衡时序参量在一维坐标下的分布。由式(19)可看出,序参量在界面的性质取决于梯度能系数κi和势阱高度w这两个系数,为确定二者的关系,首先需要确定界面的厚度,界面厚度2l由下式计算:

(20)

结合式(18)可得:

(21)

ε取决于界面厚度的定义,本文认为η=0.05～0.95为界面,故ε=0.05。式(21)为界面厚度2l与梯度能系数κi、势阱高度w的关系式,为获得确切的系数值,还需要确定界面能的表达式。

取向为i、j的两晶粒的界面能σGB可通过式(22)计算:

(22)

本文认为梯度能系数各向同性,即κi=κj,结合式(18),式(22)可化简为:

(23)

进一步计算可得:

(24)

由式(21)、(24)可得梯度能系数κ、势阱高度w表达式:

(25)

(26)

1.3 晶界溶度分布及溶质拖曳

基于Cahn-Hilliard[14]扩散方程,推导了平衡状态下溶质在晶界上的分布,结果与式(4)的约束条件相符合,此外还得到了非平衡状态下与Cha[7]表达式相类似的溶质分布。

基于Allen-Cahn方程[13]推导了与圆形晶粒收缩相关的动力学方程,结果与Fan[15]的研究相一致,获得了圆形晶粒收缩的驱动力表达式。

结合溶质在晶界分离引起的耗散能ΔGSDE的定义对附加拖曳项的形式进行如下推导。

由Cahn-Hilliard扩散方程(式(11))可得:

(27)

其中:fcc=∂2f/∂c2;fcη=∂2f/∂c∂η;fcη/fcc=P′(η)(cGB-cm)[8]。将其代入式(4)、(27)可得:

(28)

平衡时dc/dt=0,在一维坐标下对式(28)积分得:

(29)

由边界条件晶粒内dc/dx=0、dη/dx=0得A=0。对式(29)进一步积分得c=cm(1+(Ke-1)P(η)),与式(4)相同。

非平衡时dc/dt≠0,溶质分布可由下式推导:

(30)

结合式(28)可得:

(31)

在一维坐标系下对式(31)积分得:

(32)

由边界条件晶粒内dfc/dx=0、c=cm得A=cm。

(33)

式(33)的解为:

(34)

以二维圆形晶粒为例,无拖曳阻力的界面迁移速率与曲率1/r呈线性关系[15],界面迁移速率可表示为v=-(dη/dt)/(dη/dr),结合式(10)可得:

(35)

m为常数时,式(18)成立,无溶质阻力作用,界面迁移速率表示为:

(36)

式(35)左右同时乘以dηi/dr,再积分得:

(37)

式(37)右边为界面驱动力,考虑到界面由i、j两组序参量组成,结合式(23),总驱动力FV可由下式表示:

(38)

在界面迁移速率v下,溶质在晶界分布引起的耗散能ΔGSDE满足以下关系式[16]:

(39)

本工作将m设为常数,SDE耗散能ΔGSDE以附加项的形式作用在界面迁移过程中,表达式如下:

(40)

其中,φi为拖曳附加项。将φi代入式(35)中,左右同时乘以dηi/dr,再积分,可得:

(41)

式(41)右侧第二项作为拖曳项应与式(39)具有相同的形式,由此可得φi的表达式:

(42)

由式(18)、(21)可得dηi/dx表达式,再结合式(32)可得:

(43)

忽略式(3)中过剩自由能项和磁贡献自由能项,fcc=RT/c(1-c),φi的简化表达式如下:

(44)

结合溶质分布(式(34))可计算出不同界面迁移速率v下耗散能沿晶界的轴向分布。在实际模拟过程中界面迁移速率v不是一个人为定义的值,式(44)难于用于模拟,故采用式(43)第一个等式右项作为拖曳项φi的表达式。

1.4 模拟方法

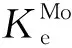
表1 模拟参数Tabal 1 Simulation parameter

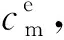
为研究迁移晶界的SDE,本工作在二维网格中设立了一个圆形晶粒。模拟圆形晶粒收缩不涉及过多取向的序参量,只包含晶粒内和晶粒外两种取向,故序参量取向数n可设为2。

2 结果与讨论

2.1 界面能分布

序参量平衡分布如图1所示,其中理论计算值为采用序参量分布式(式(19))计算所得。由图1可见,晶界半厚度l分别取5、7.5、10 nm,界面能σGB=0.65 J/m2时,序参量的相场模拟结果与理论计算结果吻合较好。晶界上仅存在i、j两个序参量不为0,且关于y=0.5对称,在晶界中心ηi=ηj=0.5,x=0是序参量延x轴分布的拐点,满足序参量平衡性质。

系统网格尺寸不变,晶界厚度越大,界面能的模拟曲线越趋近于平滑。σGB=0.65 J/m2时界面能沿x轴的分布示于图2。由图2可见,晶界占据的网格越多,其界面能峰值越小。

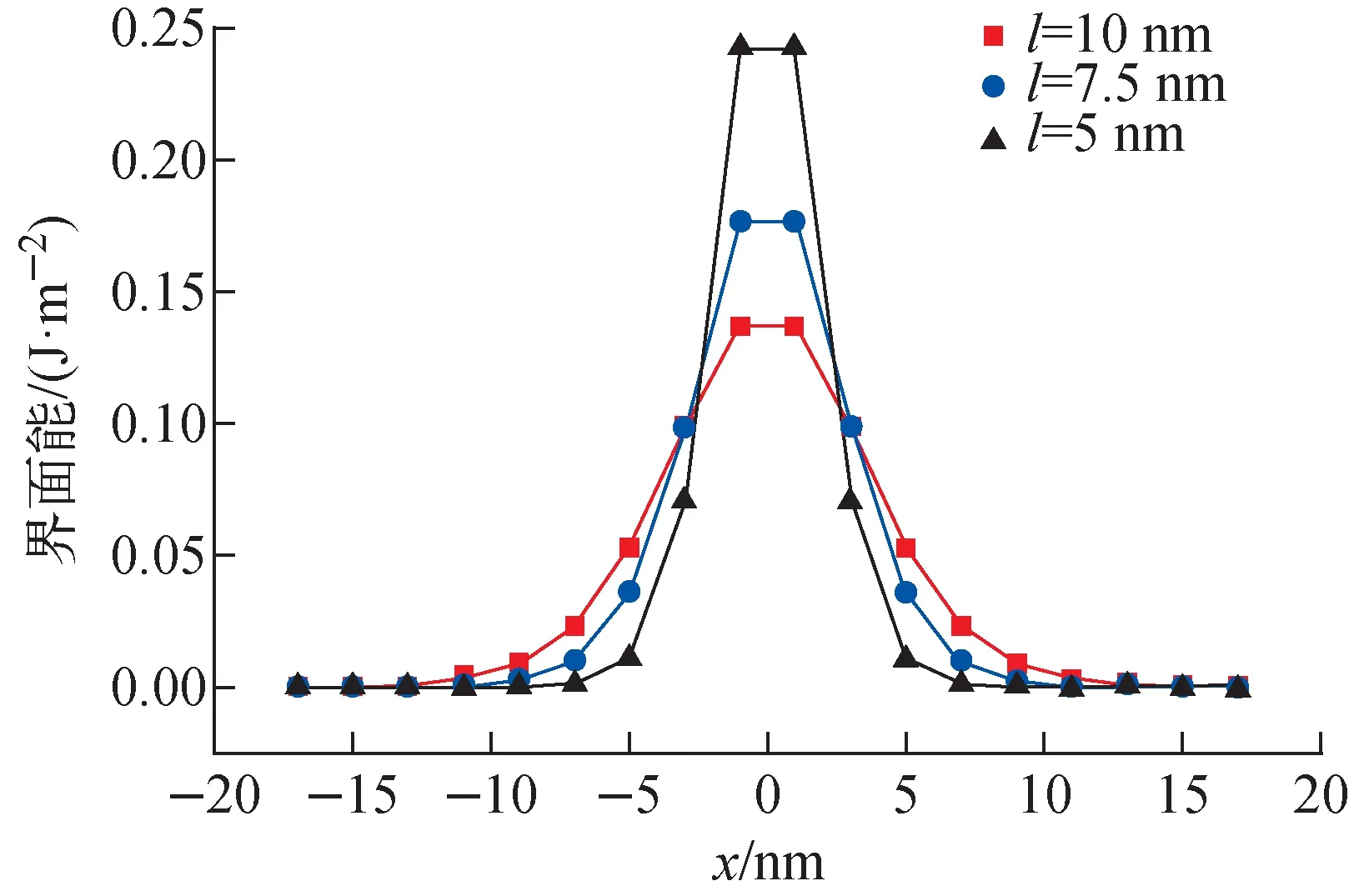
图2 不同界面厚度能量分布Fig.2 Energy distribution at different interface thicknesses

2.2 晶界处溶质浓度分布

溶质在晶界处的偏析程度与结合能有关,同时也受温度影响。温度1 100 K时不同界面迁移速率下Mo、Nb元素在α铁晶界分布的模拟结果显示,稳态时,晶界处溶质峰值最大,峰值由式(7)计算获得。稳态界面迁移速率分别为0.5、1.0、10.0 μm/s时Nb在晶界处的分布示于图3。晶界半厚度l取10 nm,运动方向沿x正轴。由图3可见,随着界面迁移速率的增加,Nb在晶界处的偏析逐渐减少,界面迁移速率为10 μm/s时,溶质偏析趋于0,这是由于Nb的扩散速率远低于界面迁移速率。图3与Cha等[7]计算的溶质分布随界面迁移速率的变化趋势相一致。

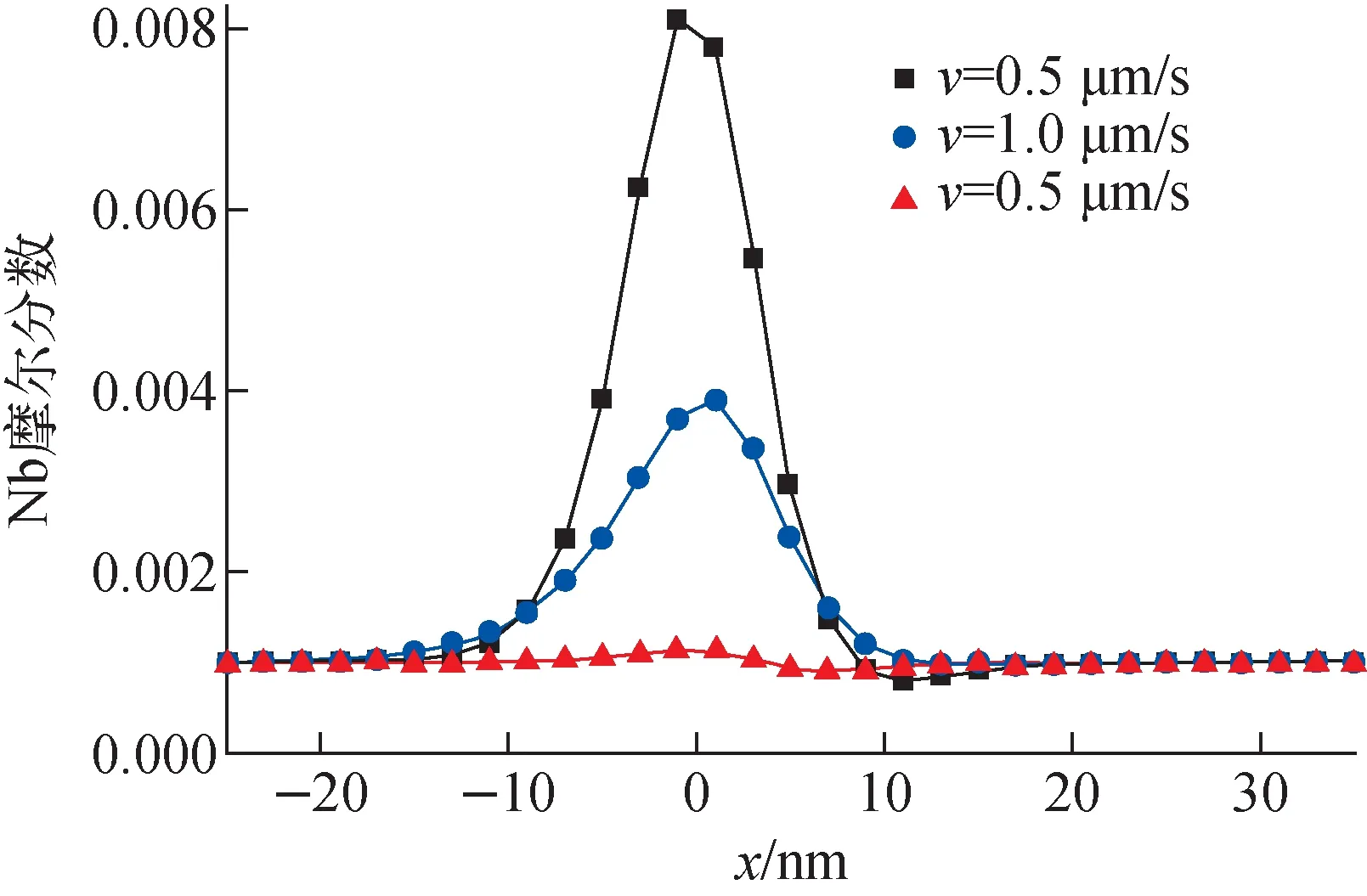
图3 不同界面迁移速率下溶质Nb的分布Fig.3 Distribution of solute Nb at different interfacial migration rates

Mo的在晶界处的偏析示于图4。对比图3可知,Mo的变化趋势与Nb相同,即随着界面迁移速率的增加,Mo在晶界偏析减小。相对于Nb,Mo与α铁晶界的结合能更小,静态时,晶界处溶质峰值也小于Nb的偏析程度。

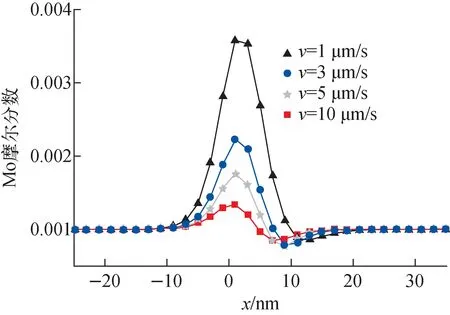
图4 不同界面迁移速率下溶质Mo的分布Fig.4 Distribution of solute Mo at different interfacial migration rates

本工作中界面迁移速率满足式(37),驱动力满足式(38),模拟时在网格中设立一个半径为160 nm的圆形晶粒,对应的界面迁移速率为0.504 mm/s,驱动力为28.8 J/mol,随着晶粒的收缩,界面迁移速率和驱动力逐渐增加,在半径为50 nm时,对应的界面迁移速率和驱动力分别达到1.61 mm/s和92.17 J/mol。

首先模拟了无SDE的晶粒收缩,同时为了观察到溶质沿晶界的分布,式(37)中的界面迁移系数乘以5×10-3,以控制界面迁移速率在SDE的作用范围内,在模拟的前20步,增大溶质扩散系数,使溶质在晶界处的偏析达到平衡。值得注意的是模拟中未引入拖曳项,界面迁移速率与曲率保持线性关系。圆形晶粒收缩过程中溶质在晶界处的分布示于图5。与经典稳态假设溶质拖曳模型[16]相比,相场方法观察到溶质的分离过程为:随着晶粒收缩,溶质在晶界处的峰值逐渐减小,部分溶质滞留在晶界后方。

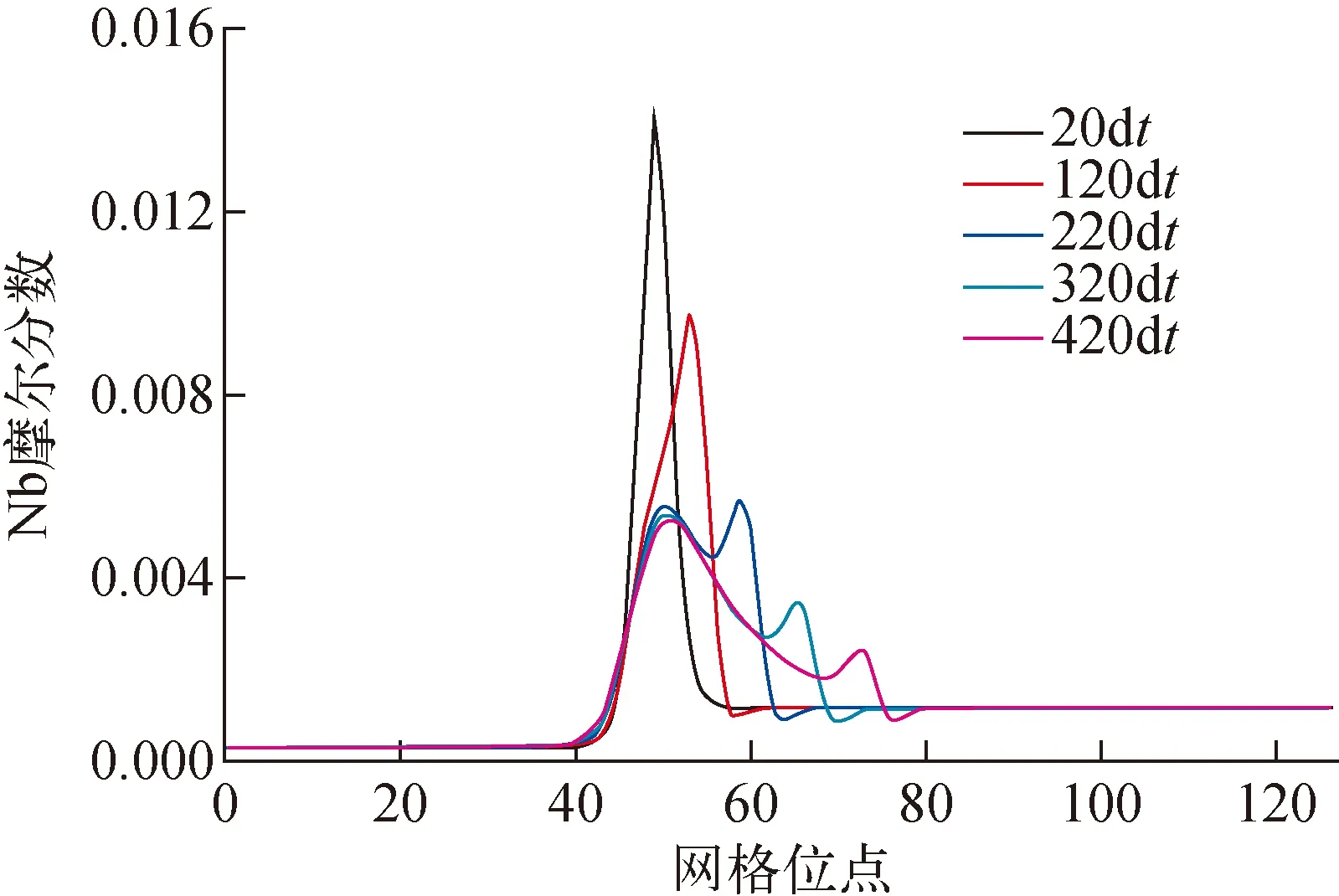
图5 溶质的分离过程Fig.5 Separation process of solute

晶粒收缩过程中界面迁移速率、驱动力和SDE耗散能(ΔGSDE)随时间的变化示于图6。由图6可知,随着圆形晶粒曲率的增加,驱动力增加,SDE耗散能先增后减,界面迁移速率的加速度取决于这两者的差值,在0.01～0.04 s时间段,驱动力与溶质耗散能之差近似为常数,故界面迁移速率在该时间段呈线性增加。0.065 s左右,SDE耗散能随界面迁移速率的增加开始下降,之后圆晶快速收缩,在很短的时间内完成如图5所示溶质分离过程。图6表明,溶质发挥拖曳作用不仅受界面迁移速率的影响,还和晶界驱动力密切相关,而相场方法能很好地模拟非稳态的SDE过程。

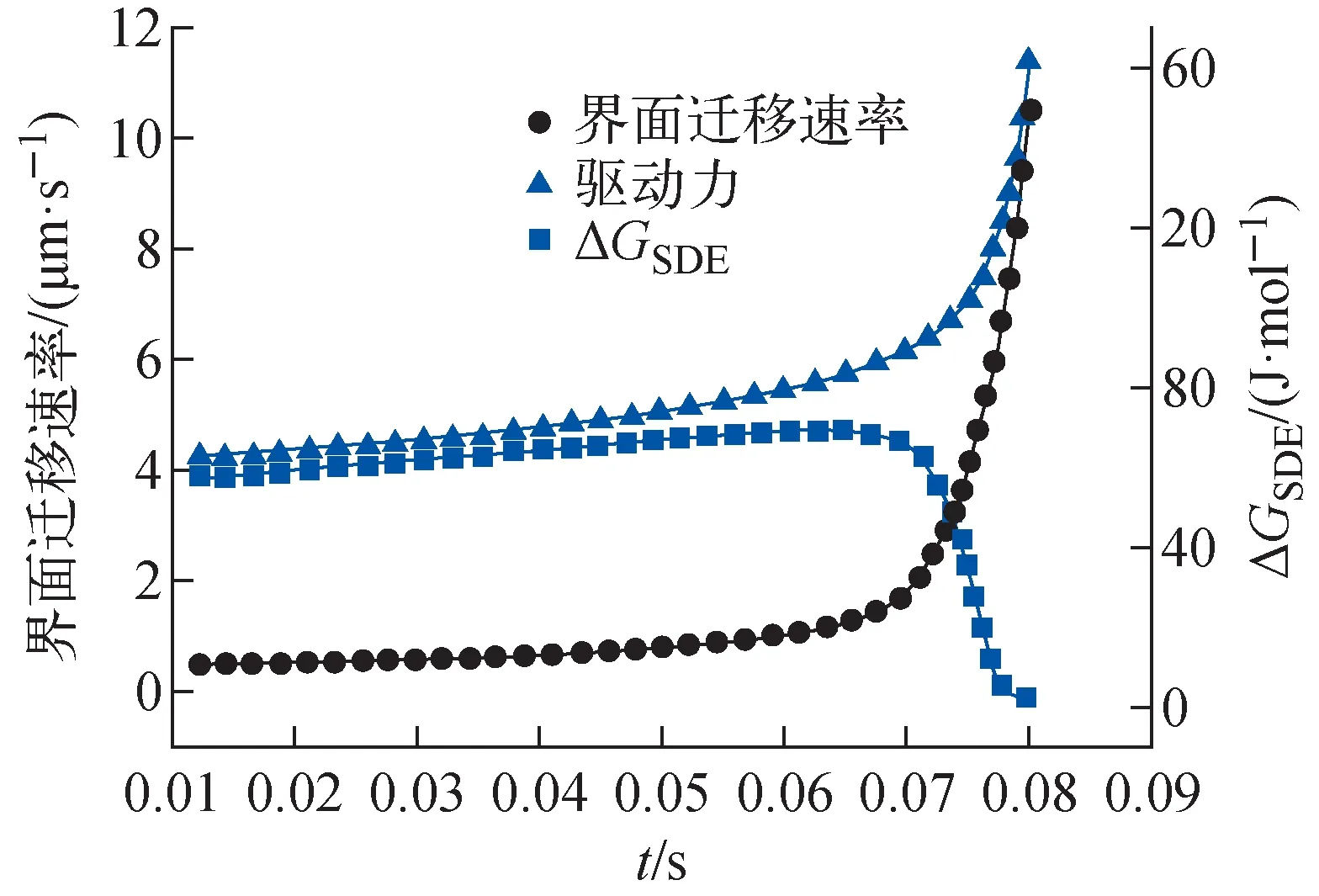
图6 圆形晶粒收缩中界面迁移速率、驱动力和SDE耗散能随时间的变化Fig.6 Time evolution of interface migration rate, driving force, and SDE dissipation during circular grain shrinkage

圆形晶粒收缩过程中SDE耗散能与界面迁移速率的关系示于图7。由图7可见,随着界面迁移速率的增加,溶度分布开始偏离平衡状态,耗散能增加,在速率为1.124 μm/s时耗散能达到峰值69.37 J/mol,之后溶质偏析减少导致耗散能降低。结合图6,在0.01～0.065 s时间段,界面迁移速率小于1.124 μm/s,界面迁移速率与SDE耗散能呈正相关,圆形晶粒缓慢收缩,大于1.124 μm/s时,速率与耗散能呈负相关,故圆形晶粒快速收缩,从0.065 s后圆形晶粒快速收缩的结果看,经典稳态假设溶质拖曳模型高估了溶质对晶界迁移的影响,这与Zhang等[18]的研究结果相一致。

图7 SDE耗散能与界面迁移速率的关系Fig.7 Relationship between v and ΔGSDE obtained by simulation

相场模拟常使用微米级的晶界来扩大计算规模,为避免晶界厚度增大导致SDE耗散能增加,保持单位面积晶界上的溶质阻力Fd不变,Fd满足关系式Fd=ΔGSDEΔx/Vm。从该式可以看出,ΔGSDE保持不变,Fd与单位网格尺寸Δx呈线性关系。

晶粒生长过程中晶界及溶质在二维网格中的分布示于图8,该二维网格的晶格尺寸如下:单位网格尺寸0.2 μm、晶界厚度2 μm、晶粒取向设置为24。从图8b可看出,溶质在晶界处偏析,部分溶质滞留在界面迁移的历史轨迹上。由图8模拟结果可知,晶粒长大初期无明显SDE,这是由于:1) 溶质在晶界偏析未达到饱和状态;2) 晶粒尺寸小,根据式(36),曲率为0.1 μm-1(r=10 μm)的圆形晶粒,其界面迁移速率为8.1 μm/s,结合图7可知,对应耗散能在5 J/mol左右,曲率小于0.05 μm-1(r>20 μm)时,才进入SDE显著作用的范围。