核心素养下的高中数学课堂“六步法”教学模式研究
2023-10-27张燕燕
张燕燕
一、 高中数学课堂“六步法”教学模式的内涵
高中数学课堂“六步法”教学模式指以提高学生数学核心素养为教学目标,以“合作学习、方法导引、分层次教学”为教学策略,以预习案、探究案、训练案三案一体为导学案设计,以学生主动参与为途径的一种数学教学模式。“六步法”是指一节数学课的六个基本教学步骤:自主学习、合作探究、展示评价、精讲导引、当堂检测、总结拓展。
二、 高中数学课堂“六步法”教学模式的实施
第一步:自主学习。课前,学生自己了解本节课学习目标,自主预习本节课内容,自主完成预习案,找出探究案中的疑难问题。例如,在学习人教A版必修一的《3.1 函数的概念及其表示》一课时,由于教材给出的函数的概念非常抽象,可以这样设计预习案:自主预习课本p60~p62的问题1、问题2、问题3、问题4,自主归纳上述问题中函数具有的共同特征,由此你能归纳出函数概念的本质特征吗?通过这样设计预习案,引导学生通过阅读与思考,自主预习,由具体例子到归纳概括,使学生先对函数的概念有一个初步认识。由于函数概念比较抽象,学生较难理解,通过上述问题的思考,可以提高学生的数学抽象素养。
第二步:合作探究。教师展示预习案答案,引入课题,各小组进行讨论,找出探究案中的疑难问题,也可以师生之间进行讨论,解决问题。例如,在学习人教A版必修一的《4.2.2 指数函数的图象和性质》一课,为归纳指数函数的图象和性质,探究案可以这样设计:

函数y=2x的图象位于x轴的上方,向左无限接近x轴,向上无限延伸,从左向右看,图象是上升的,与y轴交于(0,1)点。

探究2:在同一直角坐标系内作出若干个底数不同的指数函数y=ax(a>0,且a≠1)的图象,你能发现它们有哪些共同特征?[所有图象都位于x轴上方,向左右无限延伸;所有图象都过点(0,1);当0
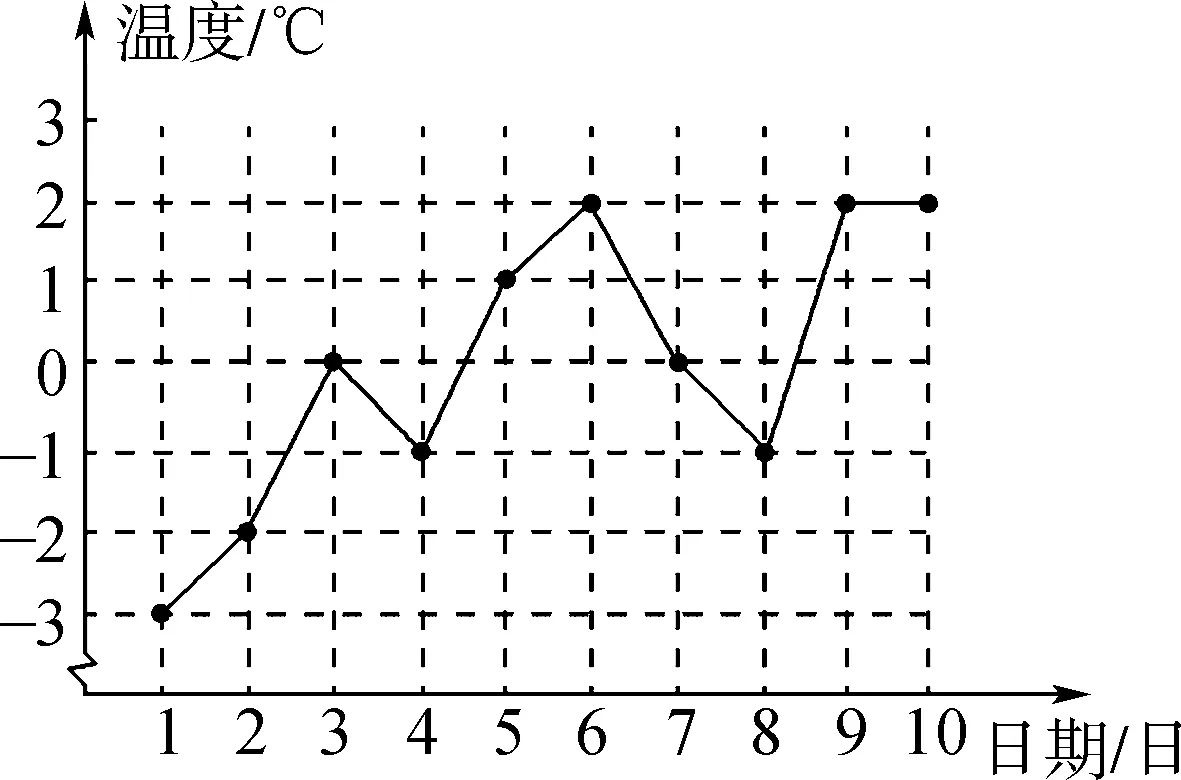
学生分组讨论,思考:通过画图象以及几何画板演示,同学们能发现什么样的规律呢?(底数分a>1和0 那么,从特殊到一般,同学们能归纳总结一下指数函数y=ax(a>1)有哪些性质? 并类比得出y=ax(0 通过这样设计探究案,可以引导学生从特殊到一般,通过自主学习与合作探究,归纳出指数函数的图象与性质,提高学生的数学抽象、逻辑推理素养。 第三步:展示评价。教师随机选取小组同学上黑板展示解题步骤,然后随机选取其他小组进行点评,师生针对展示、点评中出现的问题再讨论、再探究,再展示、点评小组加分。例如,在学习人教A版选择性必修第一册《3.3.1 抛物线及其标准方程》一课时,小组派代表演算下列题目:已知抛物线的标准方程是y2=8x,求它的焦点坐标和准线方程。变式1:已知抛物线的焦点是F(0,-4),求它的标准方程。变式2:求抛物线y2=8x上与焦点距离等于4的点的坐标。变式3:求抛物线y=ax2(a≠0)的焦点坐标及准线方程。教师给展示小组和讲解小组加分,通过该展示评价,可以提高学生的逻辑推理素养。 第五步:当堂检测。当堂检测学生独立完成情况,答案公布形式可以不拘一格,当堂检测部分的题目应突出本节课的重点,由易到难设置题目,但难度不宜过大。 比如,在学习人教A版必修第二册《9.2.2 总体百分位数的估计》这一课时,当堂检测可以这样设计: 当堂检测 1. 数据8,6,4,4,3,3,2,2,2,1的85%分位数为。 【答案】6 【解析】解:一组数8,6,4,4,3,3,2,2,2,1按从小到大的顺序排列, 可得1,2,2,2,3,3,4,4,6,8,共10个, 由10×85%=8.5, 所以,该组数据的85%分位数为第9个数6, 2. 图示为某市3月1日至3月10日的最低气温(单位:℃)情况折线统计图,由图可知这10天最低气温的第80百分位数是 ( ) A. -2 B. 0 C. 1 D. 2 【答案】D 【解析】由折线图可知,这10天的最低气温按照从小到大的排列为:-3,-2,-1,-1,0,0,1,2,2,2, 青樱跪在前头,立时膝行上前,跟着扶住晕过去的富察氏。高晞月也跟着上来,惶急道:“主子娘娘跪了一夜,怕是累着了。快去通报皇上和太后。” 故答案为D。 3. 为落实党中央的“三农”政策,某市组织该市所有乡镇干部进行了一期“三农”政策专题培训,并在培训结束时进行了结业考试。如图是该次考试成绩随机抽样样本的频率分布直方图,则下列关于这次考试成绩的估计正确的是 ( ) A. 众数为82.5 B. 80百分位数为91.7 C. 平均数为88 D. 没有一半以上干部的成绩在80~90分之间 【答案】AB 【解析】由图可知众数出现在[80,85)之间,故众数为82.5,故A正确; 由图可得该次考试成绩在90分以下所占比例为5×(0.01+0.03+0.06+0.05)=0.75, 在95分以下所占比例为5×(0.01+0.03+0.06+0.05+0.03)=0.9, 因此,第80百分位数一定位于[90,95)内, 由(0.01×72.5+0.03×77.5+0.06×82.5+0.05×87.5+0.03×92.5+0.02×97.5)×5=85.5,C错误; 由(0.06+0.05)×5=0.55>0.5,有一半以上干部的成绩在80~90分之间,D错误。 故选AB。 通过该当堂检测,可以提高学生数学运算、数据分析素养。 第六步:总结拓展。师生对本节课涉及的外延知识进行拓展,布置本节课作业(训练案)。例如,在学习人教A版选择性必修第一册《3.1.1 椭圆及其标准方程》这一课时,课堂小结完后,可以由椭圆的定义:平面内到两个定点的距离的和等于常数(大于这两个定点之间的距离)的点的轨迹是椭圆做拓展:平面内到两个定点的距离的差等于常数的点的轨迹是什么?为后面学习双曲线的定义打下基础。通过这样的拓展,能够提高学生的数学抽象、逻辑推理素养。 另外,教学过程中可以适当拓展高考真题。比如,在学习人教A版选择性必修第三册《7.1 条件概率与全概率公式》这一节时,可以拓展高考真题。 2023新高考全国1卷21: 甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮。无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8,由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5。 (1)求第2次投篮的人是乙的概率; (2)求第i次投篮的人是甲的概率; 【解析】 (1)记“第i次投篮的人是甲”为事件Ai,“第i次投篮的人是乙”为事件Bi, 所以,P(B2)=P(A1B2)+P(B1B2)=P(A1)P(B2|A1)+P(B1)P(B2|B1)=0.5×(1-0.6)+0.5×0.8=0.6。 (2)设P(Ai)=pi,依题可知,P(Bi)=1-pi,则 P(Ai+1)=P(AiAi+1)+P(BiAi+1)=P(Ai)P(Ai+1|Ai)+P(Bi)P(Ai+1|Bi), 即pi+1=0.6pi+(1-0.8)×(1-pi)=0.4pi+0.2, 该题第1问直接考查全概率公式的应用,第2问是找到递推式,构造等比数列,利用等比数列通项公式求解,第3问是根据期望公式以及数列求和公式求解,此题考查了学生数学抽象、逻辑推理素养。 在高中数学课堂中运用“六步法”教学模式目的是转变传统教学方式,突出学生主体地位,培养学生的数学核心素养,同时也是新高考背景下的一次大胆尝试和创新。
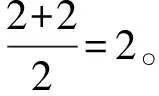

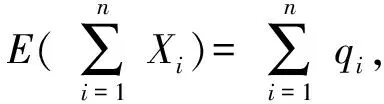
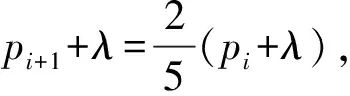
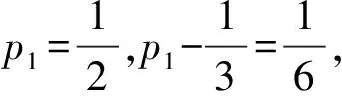
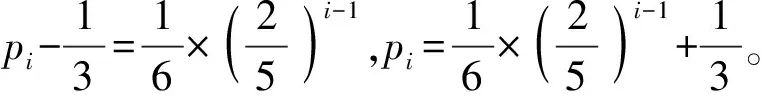

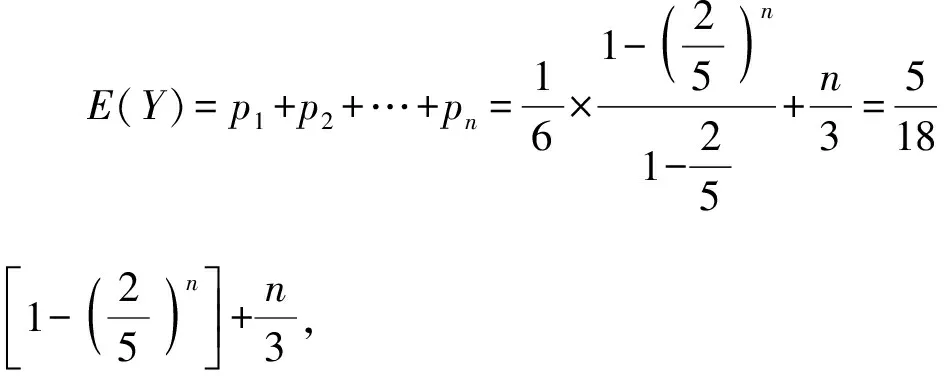
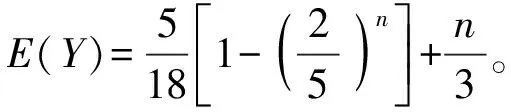
三、 结论
