煤岩体双孔爆破应力波及裂纹扩展叠加效应分析
2023-10-26徐学锋史鹏科
徐学锋 ,史鹏科
(1.河南理工大学 能源科学与工程学院,河南 焦作 454000;2.河南理工大学 河南省矿产资源绿色高效开采与综合利用重点实验室,河南 焦作 454000)
煤岩体中进行松动爆破是具有冲击地压危险的采掘面常采用的一种卸压防冲措施,炸药爆炸产生的动应力波使煤岩体产生破碎的区域,可以消除煤体的冲击危险性,使围岩中的高应力区向煤岩体深部转移[1-2]。在高瓦斯和突出矿井也经常采用炸药爆破进行煤体预裂,从而消除突出危险并提高瓦斯抽采率[3-4]。沿空留巷、小煤柱沿空掘巷中也经常采用深孔爆破的方式进行切顶卸压,为巷道围岩控制创造较低的采场矿压环境。国内外科研人员对爆破在卸压作用方面进行了大量研究,对爆破形成的裂纹扩展特征及爆破方案优化等方面也进行了研究[5-12]。现场施工中关键的技术参数就是炮眼的间距,也就是煤岩体松动裂隙区范围。
研究双孔爆破裂纹扩展规律,对选择合理的炮孔间距有重要的参考意义。王公忠等[13]研究了松软煤层双孔预裂爆破增透对瓦斯抽采范围的影响,确定了该煤层条件下的爆破孔的合理间距;赵建平等[14]认为,双孔爆破时,随着孔间距一定范围内的增大,孔心连线方向裂纹半径会逐渐增大,垂直孔心线方向裂纹半径会逐渐减小,存在最佳孔间距使裂纹贯通的同时产生最大有效破碎面积。目前的成果还缺少炮孔间距与单孔爆破裂纹半径定量关系方面的研究。
现场施工中,炮孔间距往往根据单个炮孔裂隙区半径的2 倍进行估算,另外,爆破方案一般是一次同时起爆多个炮孔,没有考虑炮孔起爆顺序不同对裂隙区贯通效果的影响。这种取值和爆破方案是否能达到炮孔间裂隙区完全贯通的爆破效果,以及如何确定合理的炮孔间距和爆破方案是目前需要继续深入研究的问题。为此,以某矿的煤层物理力学参数为基础,根据岩石动力学及爆破理论计算双孔爆破裂隙区贯通的炮眼间距,并采用LS-DYNA 软件分析耦合柱状装药条件下双孔爆破应力波及裂纹扩展叠加效应对2 个炮孔之间的裂隙区生成、贯通的影响,并分析微差爆破时裂纹的二次扩展规律,为合理地确定炮孔间距及爆破方案提供借鉴。
1 双孔爆破作用下裂隙区范围的理论分析
炮孔中炸药爆炸后,形成以炮孔中心为圆心的破碎区、裂隙区和震动区,爆破形成的裂隙区如图1。在现场松动爆破施工中,主要是确定裂隙区的范围,也就是裂隙区半径R。双孔爆破时,裂隙区会叠加在一起,双孔距离不同,裂隙区的叠加效果不同,需要确定叠加效果与炮孔距离、炮孔爆破顺序的关系。
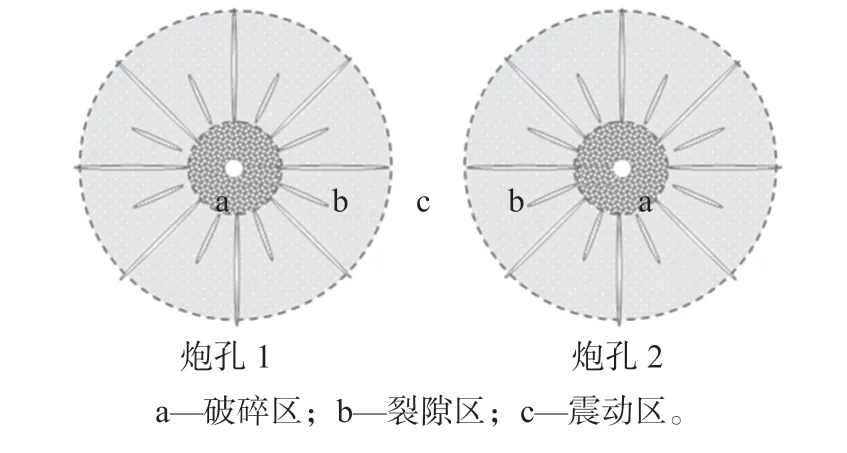
图1 爆破形成的裂隙区Fig.1 Crack zone formed by blasting
单孔耦合装药下炸药爆炸后形成的裂隙区半径R按式(1)计算[15]:
式中:σR为将要产生裂纹破坏的煤岩介质所受的应力,MPa;A为应力波的透射系数;B为与侧压系数、煤岩体动态泊松比有关的常数;σtd为煤的单轴动态抗拉强度,取1.67 MPa;σcd为煤的单轴动态抗压强度,取25 MPa;ρ0为炸药的密度,1 100 kg/m3;D为炸药的爆速,3 600 m/s;α为爆轰产物中冲击波区载荷传播衰减指数;β为煤体中应力波区载荷传播衰减指数;rb为炮孔半径,0.032 5 m。
式中:ρ为煤的密度,1 500 kg/m3;CP为煤的声速,2 200 m/s。
式中:μd为煤体的动态泊松比,0.24;λ为侧压系数,
把式(2)~式(6)代入式(1)得:
经计算,裂隙区半径R为1.67 m。所以,根据理论计算,双孔爆破时裂隙区能够贯通时,炮眼间距为3.34 m。
2 爆破应力波与裂纹扩展叠加效应数值模拟
2.1 数值模拟模型
模拟计算采用LS-DYNA 软件,LS-DYNA 属于ANSYS 软件中的动态计算模块,能较好地进行炸药爆炸、汽车撞击等冲击动力学问题的分析。本次数值模拟中,煤体材料模型使用*MAT_PLASTIC_KINEMATIC(弹塑性随动硬化模型)。分析中炸药爆炸采用Erosion 算法,煤体破坏准则采用Von Mises 准则,即计算模型中,某一个单元受到的有效应力大于煤体材料的屈服强度极限时,该单元会失效并被移去,计算模型中,破坏的单元能以裂纹的方式体现出来,从而能反应炸药爆炸过程中,煤岩体的动态应力、应变及裂纹扩展的动态演化[16]。
LS-DYNA 使用JWL 状态方程模拟炸药爆炸过程中炸药爆轰产物压力与相对体积的关系,爆轰产物压力可表示为:
式中:p为爆轰产物的压力,峰值为3 306 MPa;V为爆轰产物的相对体积,也就是爆轰产物的体积与初始体积的比值,初始取1.0;ω为格林艾森参数,即定容条件时,爆轰产物的压力相对于内能的变化率,0.30;A1、B1为炸药材料的常数,分别为120.0、0.80 GPa;R1、R2为无量纲常数,分别为4.15、0.95;E0为爆轰产物的初始比内能,4.5 GPa。
数值分析中采用二维平面应变模型,数值模型尺寸为10 m×5 m,炮孔的半径为32.5 mm,首先单孔爆破分析,然后进行双孔爆破分析,炮孔间距分别为6.0、5.0、4.0、3.4、3.0、2.5 m,模型参数与理论计算部分相同,模型边界设置成无反射边界。
2.2 单孔爆破时应力波及裂纹扩展规律
为了对比分析双孔爆破时应力波及裂纹扩展特征,首先分析单孔爆破时的应力波及裂纹扩展规律。单孔爆破时,不同时间炮孔周围的有效应力及裂纹扩展分布如图2。
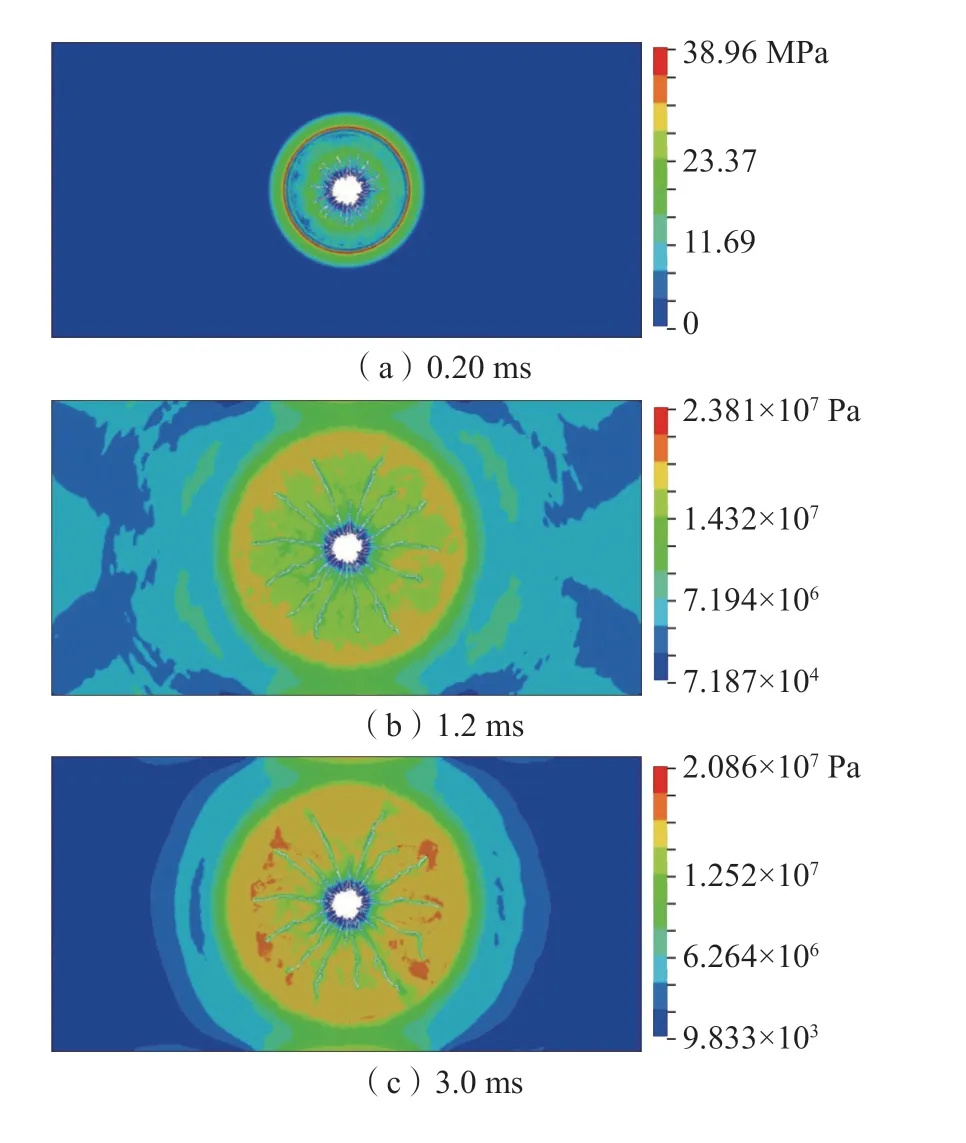
图2 炮孔周围裂隙扩展及等效应力分布Fig.2 Crack propagation and equivalent stress distribution around blast holes
从图2 看出,炸药爆破后形成的裂隙区是以炮孔中心为圆心向周围辐射扩展的圆形破坏范围,裂纹端部扩展发育过程中,形成了明显的圆环高应力区;如果这个圆环应力区的应力大于煤岩体的强度,则裂纹继续扩展,否则,裂纹扩展将终止;环形高应力区将以震动波的形式继续向周围辐射传播,从图中经过测量,裂纹扩展最大半径为1.7 m,如果双孔爆破时裂隙区贯通,炮眼间距约为3.4 m,与理论计算基本相当。选取最大的裂纹并设置3 个监测点,即:裂纹的起始单元(A)、中间单元(B)、终端单元(C)。分别提取监测点的有效应力,得到的各单元的有效应力时程变化如图3。
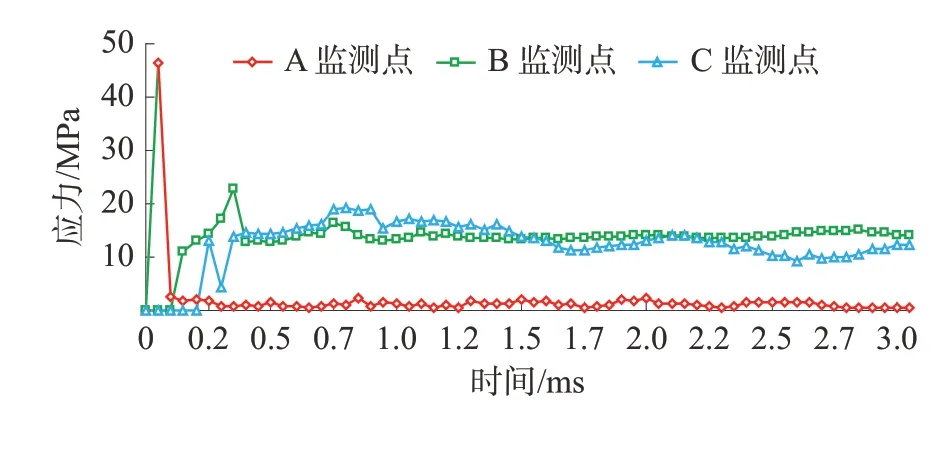
图3 最大裂纹不同位置单元有效应力时程图Fig.3 Effective stress time history of elements at different positions of maximum crack
结合图2、图3 可以看到:炸药爆破后,圆环高应力对裂纹不同位置处的作用力和作用时间不同;裂纹起始端作用力的峰值最大,作用时间短;裂纹终端煤体介质所受作用力最小;作用时间最长;作用时间从0.2 ms 开始,1.2 ms 裂纹扩展半径达到最大状态;高应力对煤体介质的作用及破坏时间约1 ms,1.2 ms 后圆环高应力产生裂纹扩展的能力基本消失,后期以震动波的形式向煤体深处传播。
2.3 双孔同时起爆时应力波及裂纹叠加规律
双孔同时爆破的数值模拟分别对不同间距的双孔爆破效果进行分析,共进行了6 次计算,每个模型计算时间为3.0 ms,左侧炮孔为炮孔1,右侧炮孔为炮孔2。各模型平衡后的裂纹扩展范围以及等效应力分布云图如图4,不同间距时最大裂纹终端单元有效应力时程变化如图5。
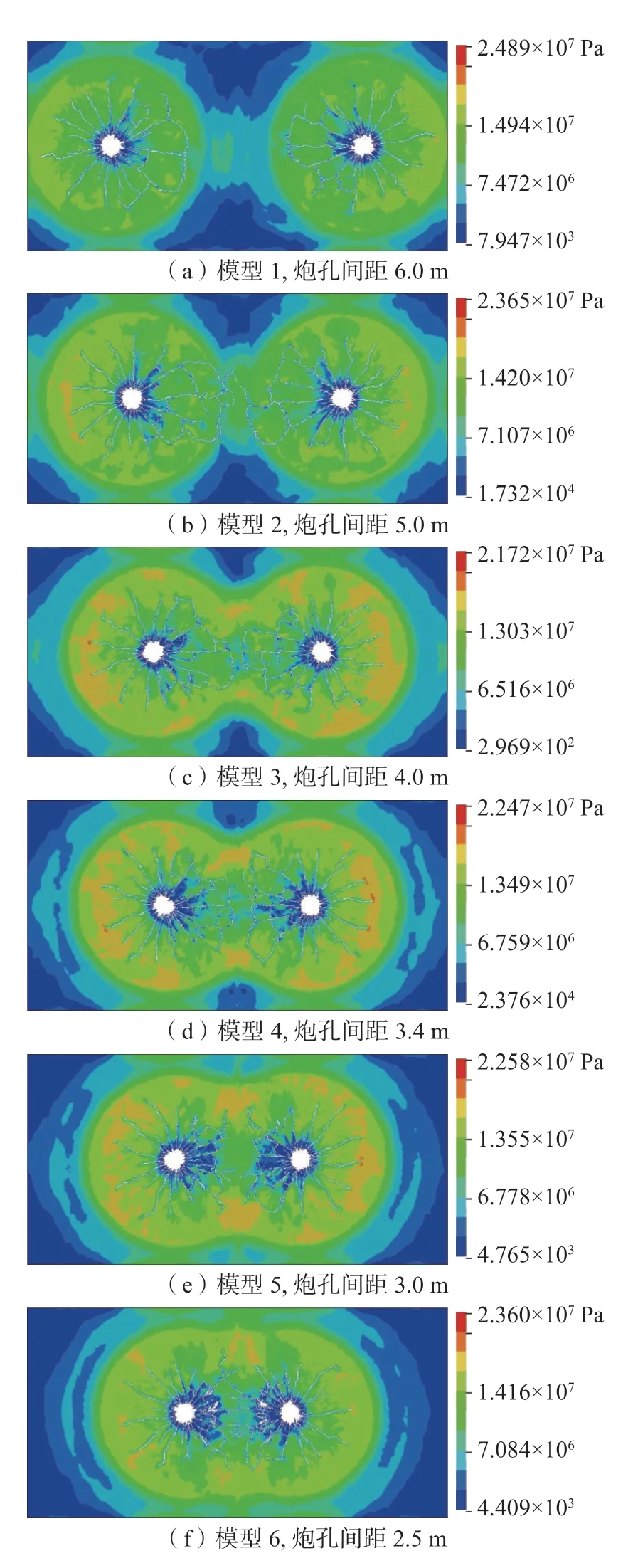
图4 双孔同时起爆不同模型裂隙及等效应力分布Fig.4 Crack propagation and equivalent stress distribution in different models with simultaneous detonation of two holes
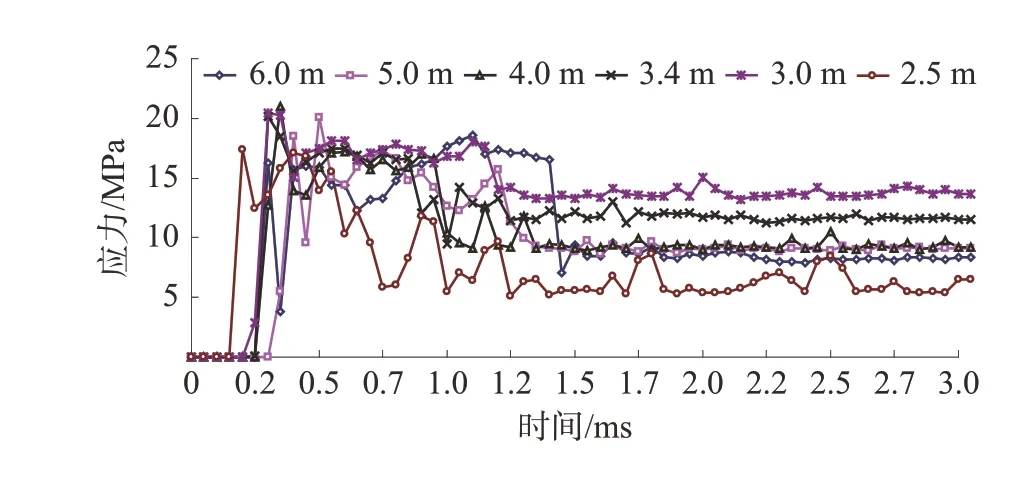
图5 双孔同时起爆不同模型最大裂纹终端有效应力时程图Fig.5 Effective stress time history of maximum crack elements in different models with simultaneous detonation of two holes
从图4 中看出:炮孔间距不同时,炮孔中间的裂隙扩展范围及规律也不同;当炮孔间距大于6.0 m 时,2 个炮孔爆破后,形成的裂隙区裂纹不能贯通;炮孔间距3.0、3.4 m(单孔爆破裂纹半径的2 倍)、4.0、5.0 m 时形成的裂隙区有少量裂纹贯通,最大的贯通裂纹长度约为5.0 m(模型2),大于单孔爆破模拟分析中估算的裂纹半径的2 倍(3.4 m),但该条件下形成的裂纹没有覆盖2 个炮孔间的全范围,也就是炮孔间的裂隙区没有完全贯通,在具有冲击地压危险的区域达不到完全卸压解危的效果;炮孔间距2.5 m 时形成的裂隙区能完全贯通,2 个炮孔中间形成裂纹均匀分布的断裂带,能达到较好的卸压解危的效果。
从图5 中看出:炮孔间距不同时裂纹终端单元的有效应力时程变化与单孔爆破相比,高应力波峰作用时间相对较长;炮孔间距2.5 m 形成的裂纹终端单元所受到的高应力作用时间从0.1 ms 至1.2 ms,作用时间约1.1 ms;炮孔间距6.0 m 形成的裂纹终端单元所受到的高应力作用时间从0.2 ms 至1.5 ms,作用时间约1.3 ms;也就是由于双孔爆破后应力波的叠加作用,增加了裂纹端部单元的受力时间,使炮孔周围裂隙区的裂纹发生二次扩展,使双孔之间的少量裂纹贯通范围大于单孔爆破后裂纹扩展半径的2 倍,但该条件下形成的裂纹没有覆盖2 个炮孔间的全范围。
综合考虑,采掘面实施爆破卸压措施时,炮孔同时爆破时,炮孔间距一般应小于单孔爆破裂纹半径的2 倍,炮孔间距取2.5 m(约为单孔估算的炮孔间距的70%),比较合理。
2.4 微差爆破时应力波及裂纹叠加规律
双孔微差爆破的数值模拟分别对不同间距的双孔爆破效果进行分析(与双孔同时爆破的模型相同,但起爆时间不同),共进行了6 次计算,左侧炮孔1 起爆3 ms 后,右侧炮孔2 起爆,每个模型计算时间为6.0 ms。各模型平衡后的裂纹扩展范围及等效应力分布云图如图6,不同间距时最大裂纹(二次扩展后形成的裂纹)终端单元有效应力时程变化如图7。
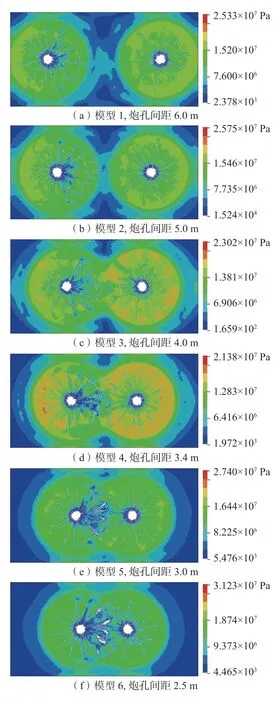
图6 双孔微差起爆不同模型裂隙及等效应力分布Fig.6 Crack propagation and equivalent stress distribution in different models with millisecond detonation of two holes
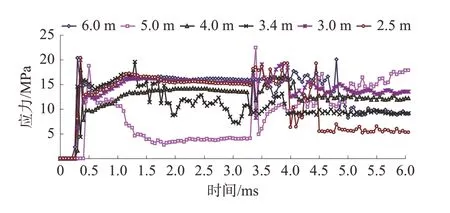
图7 双孔微差起爆不同模型最大裂纹终端有效应力时程图Fig.7 Effective stress time history of maximum crack elements in different models with millisecond detonation of two holes
从图6 中看出:微差起爆时,不同间距时双孔中间的裂纹扩展范围及规律也不同;由于炮孔1 爆破形成裂隙区后,应力波能量基本消失,炮孔2 爆破后形成裂隙区后,剩余的高能量应力波作用于炮孔1 形成的裂隙区裂纹,使炮孔1 形成的裂纹发生了二次扩展;当炮孔间距大于6 m 时,炮孔1 形成的裂纹二次扩展范围较小,炮孔间距5、4 m 时炮孔1 形成的裂纹二次扩展范围逐渐增大,炮孔1 最大的单孔裂纹长度约为2.5 m(模型2),大于单孔爆破模拟分析中的裂纹半径(1.7 m),但双孔形成的裂隙区没有完全贯通,没有覆盖2 个炮孔间的全范围,在具有冲击地压危险的区域达不到完全卸压解危的效果;炮孔间距3.4 m 时,由于先爆炮孔周围裂隙区的裂纹在后爆炮孔应力波的叠加作用下发生明显的二次扩展,炮孔间的裂隙区能够基本贯通,而炮孔间距3.0、2.5 m 时,炮孔间的裂隙区能够全部贯通并覆盖钻孔间全范围,2 个炮孔中间形成裂纹均匀分布的裂隙带,能达到较好的卸压解危的效果。
从图7 中看出:炮孔间距不同时裂纹终端单元的有效应力时程变化与双孔同时起爆时相比,应力波对裂纹形成单元的作用时间相对较长,并且出现了明显的二次应力波峰现象,二次应力波峰的应力值与第一次波峰应力值基本相当,说明炮孔1 形成的裂纹二次扩展是在炮孔2 爆破后第2 次波峰应力作用下产生的,炮孔1 爆破形成的第1 次应力波峰对后期的裂纹二次扩展没有起作用。这里面的主要原因是炮孔1 爆破后形成裂隙带,也就是在煤体中形成大量自由面,不但有利于应力波在煤体中反射产生拉应力,而且使裂纹端部煤体由三向受力变为双向受力或单向受力,强度大大降低,从而有利于裂纹二次扩展。
从能量守恒的角度分析,双孔微差起爆,炮孔1 爆破后形成裂隙区,并且为后期的裂纹二次扩展创造条件,炮孔2 爆破后不但形成裂隙区,而且使炮孔1 形成的裂纹发生二次扩展,这种爆破方式炸药爆破后的能量用于产生裂纹及裂隙区的范围较大,能量损失少。而双孔同时爆破时,高应力波在炮孔连线中间位置叠加,叠加的结果是炮孔中间的煤岩介质处于三向受力状态,不容易形成裂纹,也不容易形成裂纹的二次扩展,能量损失大。从图4、图6 对比分析看出,双孔微差起爆炮孔间距3.0 m 与双孔同时起爆炮孔间距2.5 m的裂隙区贯通效果基本相当。
综合考虑,在具有冲击地压危险的采掘工作面实施爆破卸压措施时,采用微差爆破条件下,为了达到2 个炮孔间的裂隙区完全贯通并达到较好的卸压解危效果,炮孔间距取3.0 m(约为单孔估算的炮孔间距的90%),比较合理。采用微差爆破与炮孔同时爆破相比,不但能保证爆破效果,而且还可以减少炮孔数量和爆破材料用量,是优先选择的爆破方案。
3 结 语
1)采用理论计算与数值模拟分析的单孔爆破时炮孔周围的裂隙区分布半径基本一致,以此估算双孔爆破时裂隙区能够贯通的炮眼间距约为3.4 m。
2)双孔同时爆破与单孔爆破相比,由于应力波的叠加作用,使炮孔周围裂隙区的裂纹发生二次扩展。炮孔间距3.0、3.4、4.0、5.0 m 时形成的裂隙区有少量裂纹贯通,但该条件下炮孔间的裂隙区没有完全贯通,炮孔间距2.5 m 时形成的裂隙区能完全贯通,2 个炮孔中间形成较均匀分布的裂隙带。
3)双孔微差爆破与同时爆破相比,由于先爆炮孔周围裂隙区的裂纹在后爆炮孔应力波的叠加作用下发生明显的二次扩展,炮孔间距3.4 m 时,炮孔间的裂隙区能够基本贯通,3.0、2.5 m 时形成的裂隙区能完全贯通并覆盖钻孔间全范围。
4)综合考虑,在具有冲击地压危险的采掘工作面进行松动爆破时,炮孔间距一般应小于单孔爆破裂纹半径的2 倍(炮孔同时爆破约取单孔估算的炮孔间距的70%,微差爆破约取单孔估算的炮孔间距的90%),才能保证松动爆破效果。采用微差爆破,不但能保证爆破效果,而且还可以减少炮孔数量和爆破材料用量,是优先选择的爆破方案。
