圆光栅测角误差实时补偿方法研究*
2023-10-26孙秀照雷贤卿王笑一
孙秀照,雷贤卿,王笑一
(河南科技大学 河南省机械设计及传动系统重点实验室,河南 洛阳 471003)
0 引 言
现代数控机床通常需要采用位置反馈元件,组成闭环、半闭环的伺服控制系统[1]。
圆光栅是常用的角度位置反馈装置。圆光栅的测角精度对伺服控制系统的定位精度有直接影响。但是在圆光栅实际的应用过程中,随着其使用年限的增加,机床或仪器的一些部件会发生松动或变形,伺服系统中的圆光栅会发生偏心及倾斜现象,从而产生偏心误差及倾斜误差[2],影响机床或仪器的精度。
误差补偿是提高圆光栅测角精度的常用手段。目前常用的补偿方法包括多读数头自校准、硬件补偿和软件补偿[3]。
德国联邦物理研究院[4-6]提出了一种非均布多读数头的校准模型,将8个读数头非均布地安装在圆光栅的码盘上,采集并处理各个读数头的数据,通过分析得到各个谐波阶次的误差分量,最后得到测角系统的自校准结果;但该多读数头结构也导致了系统成本及安装难度的增加。宋宇飞等人[7]利用改进的粒子群算法,从双读头计数值中拟合得到了偏心参数,设计了一种基于区间转换和两级查找表的现场可编程逻辑门阵列(field programmable gate array,FPGA)偏心误差实时补偿模块,并在FPGA中进行了实时计数值偏心误差补偿,补偿后将计数值上传至上位机;但该方法需要数控系统的参与才能完成误差补偿。高贯斌等人[8]提出了一种基于径向基函数(radial basis function,RBF)神经网络进行转角误差补偿的方法,对圆光栅进行了标定,再用标定数据训练RBF神经网络,使用经过训练的RBF神经网络对圆光栅测角误差进行了补偿;但是该方法需要大量的误差数据样本,并对其进行必要的训练。
对于现代数控机床而言,对圆光栅误差补偿通常要在数控装置中进行,并且需要事先获得用于补偿的数据表格。
常见的误差补偿方法有2种:
1)将数据表格输入到数控系统中,并在加工过程中,应用数据表格补偿圆光栅误差,进而提高机床的加工精度;
2)将数据表格应用于数控加工G指令程序中,通过修改G指令程序,改变机床的运动轨迹,进而提高机床加工精度。
但在其实际应用过程中,以上2种方法均有不足:第1种方法需要修改数控系统中的底层参数,这项工作通常只能在机床生产厂家进行,难以在用户现场进行,在用户处使用一定年限后其精度下降,难以通过误差补偿改善精度;第2种方法针对尺寸、形状不同的被加工零件,需要进行不同的处理,即使在同一台机床上、机床使用的圆光栅误差不变,误差补偿方法也不能通用,因此,该方法费时费力、成本过高,难以得到推广应用。
针对上述问题,笔者提出一种中继式的圆光栅测角误差实时补偿方法。
首先,笔者对圆光栅测角误差补偿原理进行分析;其次,设计误差补偿模块的硬件系统和软件系统,将含有补偿模型的程序写入到误差补偿模块中;最后,对圆光栅的测角误差进行补偿,并对补偿前后的圆光栅测角误差进行对比试验,以验证笔者提出方法的有效性。
1 误差补偿原理
圆光栅系统通常由圆光栅和读数头组成。圆光栅系统的测角误差主要来源于圆光栅的刻线误差和安装误差(包括偏心、倾斜和圆光栅环变形)等[9-10]。
以上误差均对应误差频谱曲线中特定阶次的谐波成分,因此,可以利用谐波分析方法处理测角误差数据[11-14]。
在笔者计算出各阶谐波分量之后,可对测角误差函数进行合成。
合成函数如下[15-16]:
(1)
式中:Δθ为圆光栅在角度θ处的测量误差;ts为s阶谐波频率;φts为s阶谐波相位;Cts为s阶谐波幅值;l为谐波成分最高阶次,通常可取l=3。
基于式(1)给出的误差,可得到圆光栅测角误差的补偿模型,公式如下:
θ1=θ-Δθ
(2)
式中:θ为圆光栅测角系统测量值;θ1为补偿后的圆光栅实际转动角度值。
2 误差补偿模块及补偿方法
2.1 误差补偿模块
独立的中继式误差补偿模块包括硬件系统和软件系统2个部分。
2.1.1 硬件系统
误差补偿模块硬件系统功能框图如图1所示。

图1 硬件系统组成功能框图
硬件系统由信号输入模块、信号处理模块和信号输出模块3部分组成。
信号输入模块电路原理图如图2所示。

图2 信号输入模块电路原理图
为了采集高质量的脉冲信号,笔者选择德州仪器的AM26LS32差分信号缓冲器作为信号输入模块,来接收读数头输出的RS422差分电平信号,实现脉冲信号从双端差分信号到单端信号的转换。AM26LS32芯片有4路差分信号输入,笔者所用读数头为3路差分信号输出。
为了减小信号干扰,保证信号质量,在芯片空闲的正相输入引脚接4.7 kΩ上拉电阻,反相输入引脚接4.7 kΩ下拉电阻;空闲输出引脚悬空;在正反相连接的管脚间使用了100 Ω的终端电阻进行阻抗匹配,采用DB15针接口实现其与读数头的连接。
信号处理模块采用STM32FI03C8T6芯片作为主控芯片,对信号进行处理。
信号输出模块电路原理图如图3所示。

图3 信号输出模块电路原理图
信号输出模块中,德州仪器的AM26LS31差分信号驱动器用于实现脉冲信号从单端信号到双端差分信号的转换。
AM26LS31芯片的空闲输入引脚接4.7 kΩ上拉电阻,空闲输出引脚悬空。同样,在正反相连接的管脚间,使用100 Ω的终端电阻进行阻抗匹配;采用DB15针接口实现与信号接收设备的连接。
2.1.2 软件系统
误差补偿模块的软件系统功能由ARM芯片实现。
软件系统功能模块原理框图如图4所示。
软件系统由四倍频细分辨向计数模块、脉冲信号补偿模块和脉冲输出模块3部分组成。
其中,四倍频细分辨向计数模块实现对转化后的单端信号进行四倍频处理和辨向计数。该模块设计中选择ARM单片机定时器的编码器模式来接收高速的圆光栅信号,定时器频率为36 MHz,滤波系数设为2,使得ARM单片机可接收频率3 MHz以下的脉冲信号。STM32定时器为16位,计数的最大值为65 536,超过这个数值定时器就会发生溢出中断。所以笔者选择另一定时器每隔400 μs去查询接收信号定时器的控制寄存器CR1的位4,通过查询该位等于0或1来判断定时器计数是上溢出还是下溢出,以此辨别圆光栅的转动方向。
同时,另一定时器要查询接收信号定时器的计数值和溢出次数,通过查询到的接收信号定时器的溢出次数和计数值,可计算出圆光栅当前位置。
计算方法如下:
(3)
式中:x为接收信号定时器的溢出次数;cnt为接收信号定时器的计数值;Pulse为圆光栅当前位置的脉冲数。
脉冲信号补偿模块实现对输入的圆光栅信号进行误差补偿。该模块将四倍频细分辨向计数模块计算得出的圆光栅位置信息代入到误差补偿算法中,实现补偿功能。
脉冲输出模块将补偿后的圆光栅信号以方波脉冲的形式输出给AM26LS31芯片。输出方式使用ARM单片机定时器的主从定时器门控模式。主定时器输出模式设置为输出比较翻转触发模式,从定时器设置为从模式的门控模式。
圆光栅正反转时的波形示意图如图5所示。
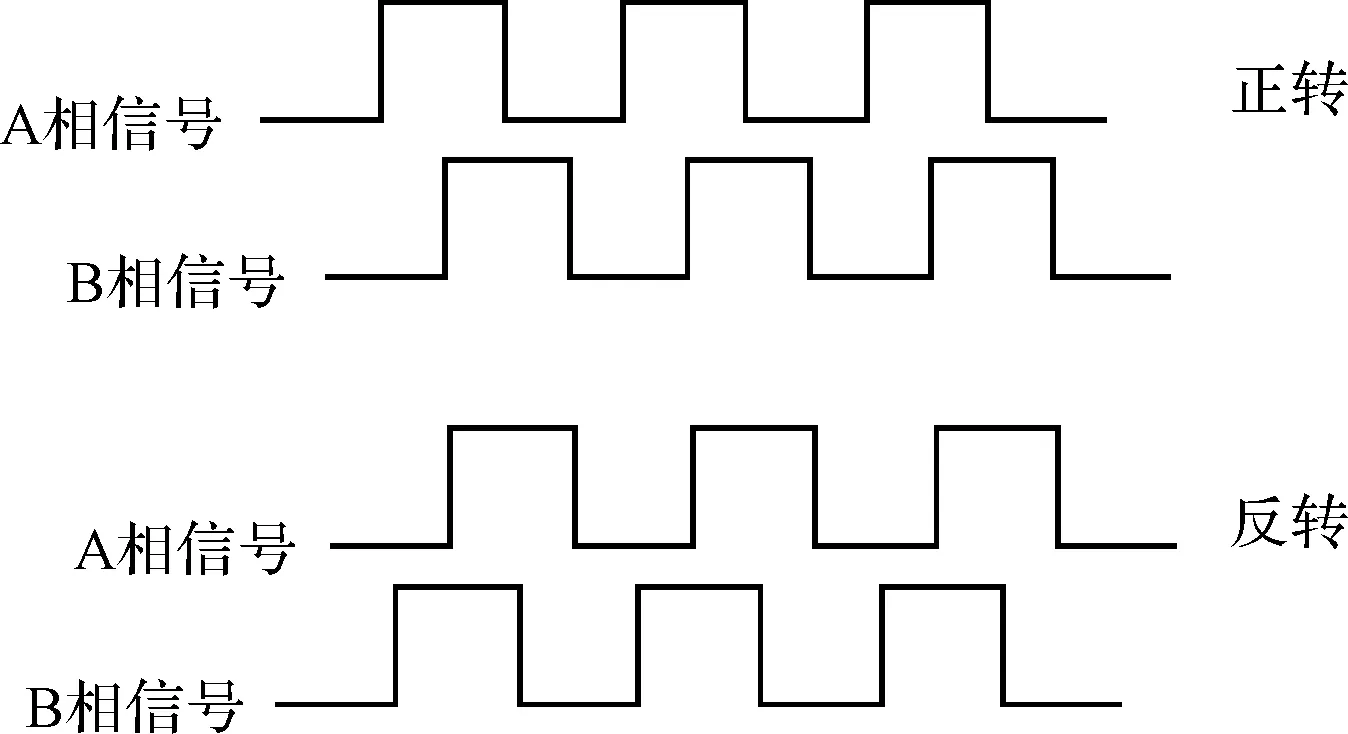
图5 圆光栅波形示意图
主定时器的CH1和CH2引脚输出正交脉冲,需要输出的脉冲个数写入到从定时器的捕获比较寄存器中,从定时器计数完成后会在中断函数中关闭主从定时器使能,以等待下一次脉冲输出命令。在软件中通过定义主定时器的捕获比较寄存器的数值来控制AB两相的相位差,达到输出正交脉冲的目的。
示波器采集到误差补偿模块输出的AB两相单端信号的脉冲波形,如图6所示。
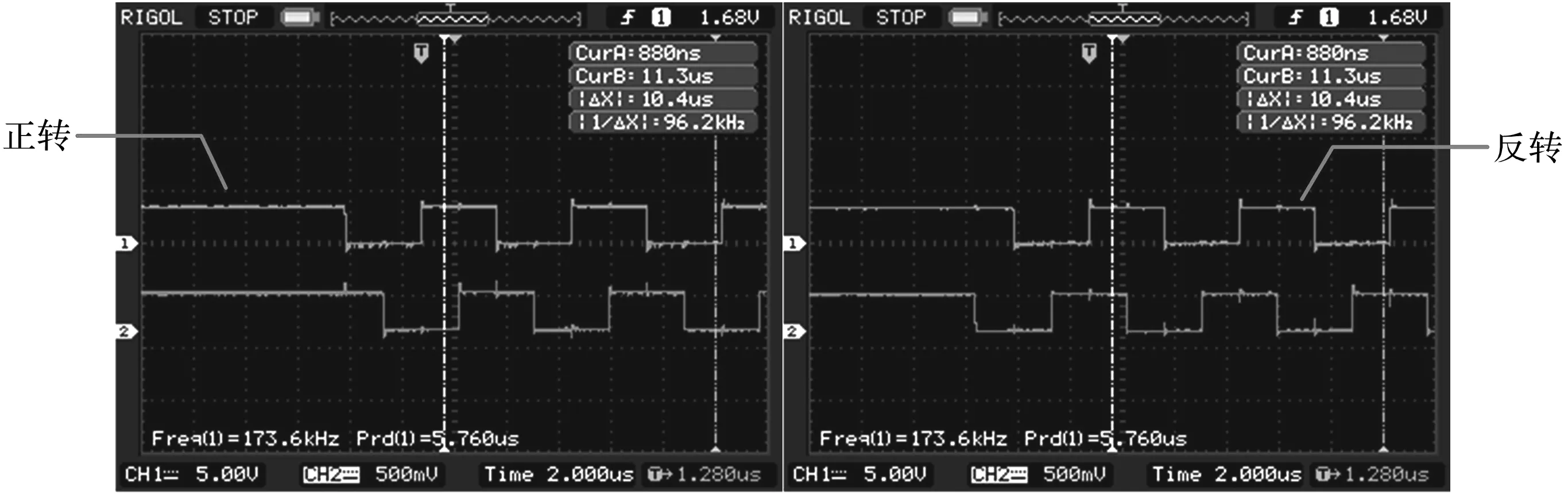
图6 误差补偿模块输出波形图
图6中,CH1通道为A相信号,CH2通道为B相信号。可见实际输出信号为正交脉冲信号。
2.2 补偿方法
笔者提出了一种中继式的圆光栅测角误差实时补偿方法,即通过独立的中继式误差补偿模块接收圆光栅的差分信号,并执行误差补偿功能,补偿后以原始数据的传送方式向外发送。
具体实施步骤如下:
1)使用雷尼绍回转校准装置对待测圆光栅进行标定,采集圆光栅的原始误差数据。
校准装置如图7所示。

图7 雷尼绍校准装置
校准装置由激光干涉仪XL-80、干涉镜、角度测量仪XR-20组成。校准装置测角精度±1″,满足试验要求。
试验用圆光栅系统如图8所示。

图8 试验用圆光栅系统
圆光栅系统由4个读数头和圆光栅组成。在试验过程中只需用到其中的一个读数头。
笔者选用雷尼绍公司的VIONIC系列读数头,其1 000倍电子细分误差最大不超过20 nm。圆光栅为雷尼绍的RESM系列的增量式圆光栅,直径为52 mm,刻线数为8 192条;
2)利用MATLAB对采集到的原始误差数据进行傅里叶拟合,得到谐波拟合函数;
3)将谐波拟合函数和误差补偿模型写入到误差补偿模块内;
4)信号输入模块接收单读数头输出的圆光栅的实时位置信息;
5)误差补偿模块将位置信息代入到谐波误差补偿算法公式中,对圆光栅信号进行补偿;
6)误差补偿模块将补偿后的数据以原始数据的发送方式向外发送。
3 试验验证
3.1 试验系统
补偿试验在实验室的隔振平台上进行。
试验系统由雷尼绍的回转校准装置、圆光栅系统、误差补偿模块、运动控制器、直驱电机和上位机组成。
试验系统如图9所示。

图9 试验系统
试验中,上位机与运动控制器利用PCI总线通信,控制直驱电机做点位运动。直驱电机旋转带动圆光栅及XR-20旋转。由读数头读取圆光栅位置信息,由激光干涉仪获取XR-20的旋转角度并由上位机读取该数据。读数头将圆光栅位置信息输出给误差补偿模块。
采用误差补偿模块,把补偿后的圆光栅位置信息输出给运动控制器(以差分信号的形式)。上位机得到实时的圆光栅位置信息以及激光干涉仪的更高精度的测量数据,产生用于误差补偿的数据表格。
3.2 试验数据及分析
3.2.1 数据采集
笔者利用雷尼绍校准回转装置对圆光栅进行标定。标定圆光栅的范围为0°~360°,步距为10°,共采集到37个数据。取圆光栅读数与激光干涉仪的读数的差值作为原始误差数据。
圆光栅测角误差测量结果(原始误差)如图10所示。
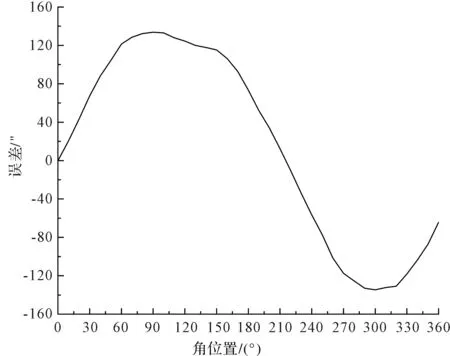
图10 圆光栅测角误差
由测量结果可知,读数头的测角误差最大值为134.59″。
为得到环境因素对圆光栅读数头的测角误差产生的影响的规律,笔者进行了读数头测量数据漂移试验。试验中每隔200 ms采集一次读数头数据。
在1 min内采集的数据如图11所示。

图11 读数头漂移误差
由图11可以看到:环境变化等因素造成的随机误差峰值在±2″以内,会对圆光栅的测角精度会造成一定的影响。
3.2.2 误差补偿模型
误差补偿过程中,要用到大量浮点数运算,在ARM单片机采用的串行工作模式下,会占用大量运算时间。
为提高补偿运算速度,在试验中,笔者选择三阶谐波函数作为补偿模型,利用MATLAB的拟合工具,对测角误差数据进行三阶傅里叶拟合。拟合残差如图12所示。
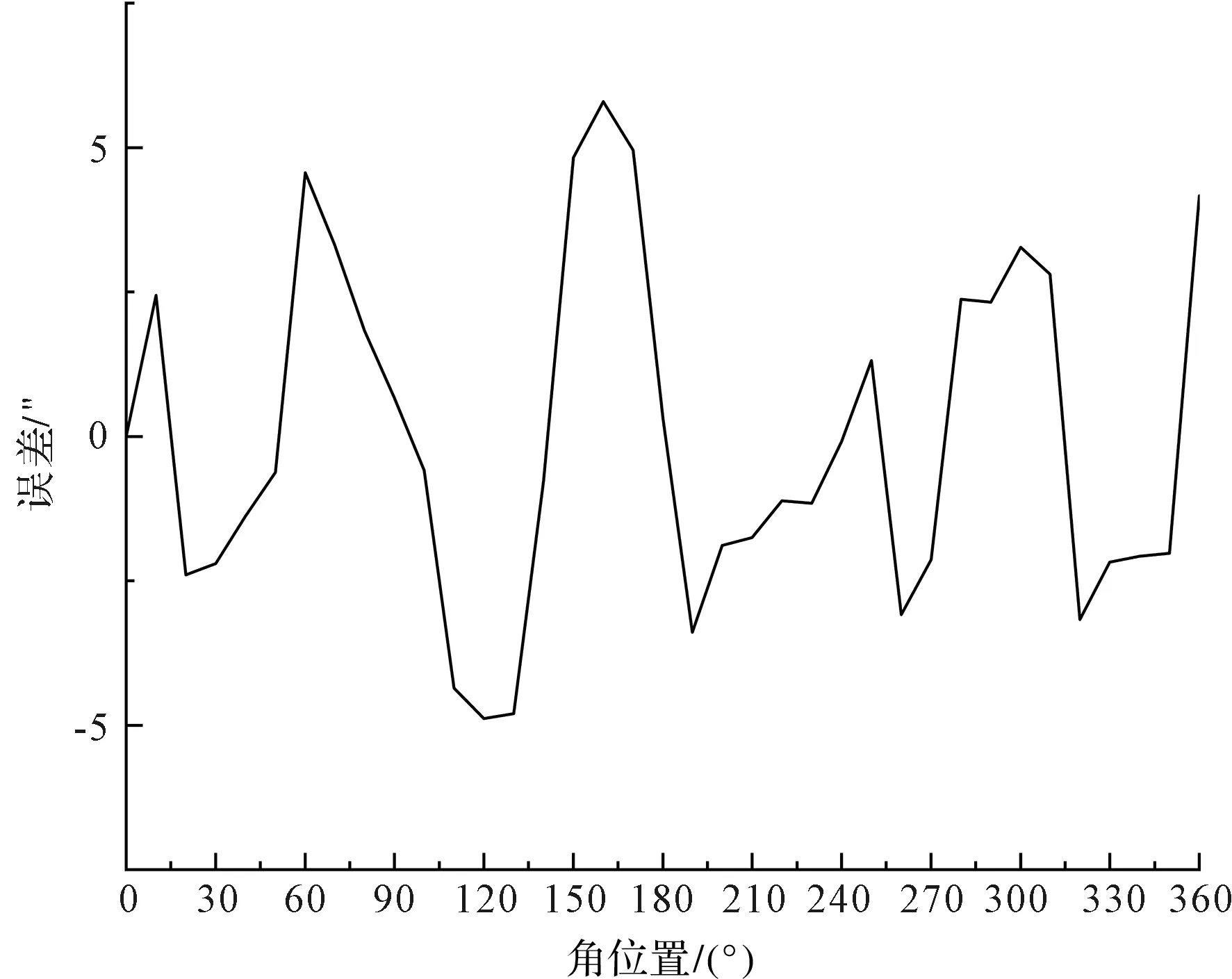
图12 拟合残差
由拟合残差结果可知,拟合残差峰值为5.79″。
3.2.3 误差补偿
笔者将上述步骤得到的误差补偿模型写入到误差补偿模块内,对输入的圆光栅信号进行实时补偿。
补偿后的圆光栅测角误差如图13所示。
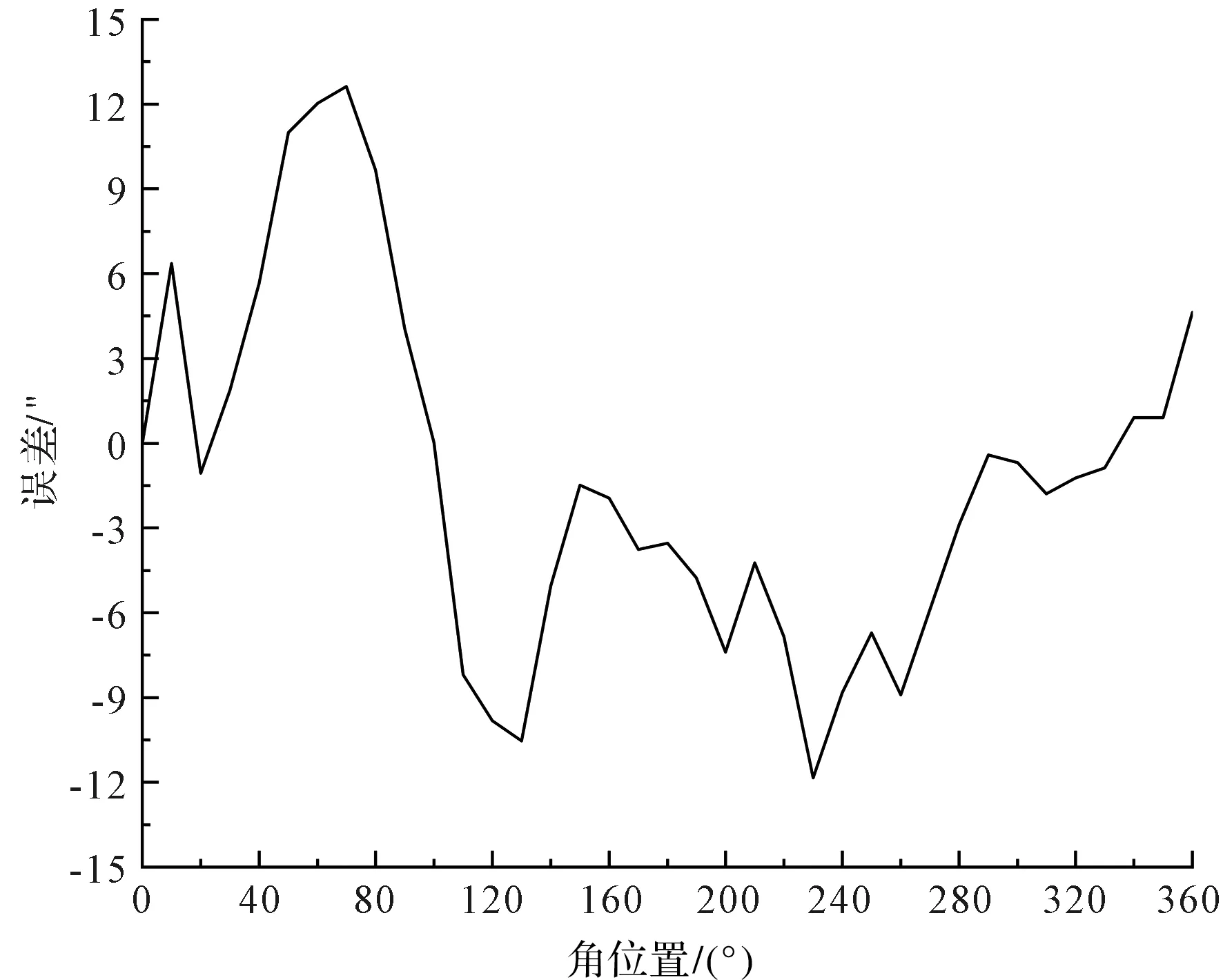
图13 补偿后测角误差
补偿后的试验数据表明:在拟合误差峰值为5.79″、随机误差峰值为±2″的条件下,笔者提出的方法将测角误差峰值由补偿前的134.59″减小到了补偿后的12.62″,显著提升了圆光栅的测角精度。
4 结束语
一些机床和精密仪器由于没有位置测量元件误差补偿功能,无法进行圆光栅的误差在线补偿。针对这一问题,笔者提出了一种中继式的圆光栅测角误差实时补偿方法。
首先,对圆光栅测角误差补偿原理进行分析;其次,设计误差补偿模块的硬件系统和软件系统,将含有补偿模型的程序写入到误差补偿模块中;最后,对圆光栅的测角误差进行补偿,并对补偿前后的圆光栅测角误差进行对比试验。
研究结果如下:
1)所设计的硬件电路可实现差分式光栅信号的接收和发送目标,可实现光栅误差的在线补偿目标;
2)采用误差曲线谐波拟合方法可对实测测角误差数据进行拟合,得到了误差补偿模型;当谐波次数≤3时,算法所需的运算能力可由ARM单片机提供,可完成误差的实时补偿;
3)试验中,采用该方法能够将测角精度提高一个数量级,对测角误差最大值134.59″的圆光栅进行补偿后,其误差最大值减小到12.62″,圆光栅测角精度得到显著提高。
由于试验所采用ARM芯片的运算能力有限,该方法目前只使用了三阶谐波补偿函数,补偿精度还有较大的提升空间。
在下一阶段,笔者将采用FPGA作为运算平台进行试验,以满足伺服控制系统高精度、高实时性的要求。
