考虑最短转弯半径的无人机区域覆盖航迹规划

宋志强， 陈少博

（1.无锡学院自动化学院，江苏 无锡 214105；2.南京信息工程大学滨江学院自动化学院，江苏 无锡 214105）

0 引言

无人机应用越来越广泛，将无人机应用于测绘［1］、环境监测［2］、搜救［3］、精确农业［4］等，得益于无人机机载传感器获取地面信息并实现区域覆盖。此类应用中，高效的无人机航迹规划算法非常重要，从图像提取信息的时间、成本和质量直接关系到规划质量。在各种应用中，二维覆盖尤为成功。覆盖任务分两步骤进行，一是准备阶段，选择运载工具、相机配置和任务规划，二是执行阶段，无人机自主飞行并收集数据。要实现任务的完全自动化，就必须解决任务规划问题，其核心是覆盖航迹规划，定义为计算无人机航迹的任务，使得感兴趣区域（Region of Interest，ROI）的所有点都能被监测到［5］。现有的规划器没有考虑连接路径，即无人机起飞点到ROI 的路径以及从ROI 到无人机着陆点的航迹，不考虑连接路径通常并不是无人机执行任务的完整路径，且当任务由多个ROI 和多个连接路径组成时，路径长度增量更大。因此，有必要规划一条考虑任务起点和终点的路径。此外，固定翼无人机的最小转弯半径也是需要考虑的因素。

直线飞行形成来回航迹（Back and Forth Path，BFP）需要计算路线的方向，以往的研究仅在舍弃起点和终点的航线上定义路径最优性。一般来说，如果想保持BFP作为覆盖模式，必须结合起点、终点提供最小成本的BFP 执行搜索。一个简单的策略是循环BFP直到出现最小值，但这不是有效策略。本文提出一种改进的旋转卡尺路径规划算法，考虑无人机的起飞点和着陆点，并考虑固定翼无人机的最小转弯半径，使算法更具实用性。

Huang［6］提出一种移动机器人排雷作业的覆盖方法，使用无人机覆盖航迹规划大多遵循Huang 定义的最优准则，即航线数量最少的路径为最优路径。Huang提出机器人来回运动的扫描方向必须垂直于感兴趣区域多边形的最小宽度，方法没有考虑从起点到感兴趣区域的距离。一些文献研究非凸区域的覆盖问题，涉及凹多边形凸分解［7］，Li 等［8］将非凸ROI 分解为凸单元，通过设置垂直于单元最小宽度的飞行线来计算路径的最优方向。王自亮等［9］采用对凹多形区域直接遍历的方法，实现对区域的覆盖，但凹多边形区域存在狭长区域时，容易产生多个转弯路径。王红星等［10］针对凹多边形区域进行凸分解，研究区域覆盖算法，使无人机对指定区域进行覆盖搜索。刘旭林等［11］选取凹多边形及其凸包的边所在的方向分别为主方向，得到全局最优解。Coombes 等［12］考虑风速对无人机航迹的影响，旨在减少固定翼飞机测量飞行时间。多无人机协同搜索［13-15］可提高任务的完成速度，一般的方法是将其分为区域划分和区域覆盖搜索路径规划两个子问题处理。Fevgas 等［16］通过无人机的合作策略以实现节能的覆盖航迹规划。对无人机区域覆盖中的转弯控制［17-19］，也是值得研究的问题。文献［20］中提出一种包含无人机飞行起点和终点的边-点来回扫描覆盖航迹规划，但主要针对凸多边形区域，且没有考虑固定翼无人机的最小转弯半径。

综上，以前的方法很少考虑无人机起飞点到达ROI的连接路径，考虑连接路径和ROI凹凸性以及固定翼无人机最小转弯半径的覆盖航迹规划，更具实用价值。

1 覆盖问题描述

1.1 感兴趣区域

假设ROI 为二维平面图形Q=｛V，E｝，其中V=｛1，2，…，n｝为顶点集，E=｛（1，2），…，（n-1，n），（n，1）｝为边集。

对于凸多边形区域，第一步是寻找覆盖最优方向，其垂直于多边型区域的最小高度，在这一方向上，区域可被最少行覆盖，即无人机的转弯次数也最少，完全覆盖航迹如图1 所示。转弯次数和覆盖指定区域的时间直接相关，具有最少转弯次数的航线在航线长度、无人机续航时间、能量消耗等方面更优。

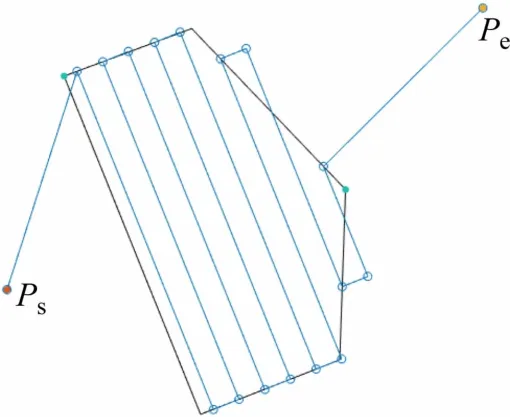
图1 完全覆盖航迹示例

1.2 航线方向设置

假设无人机将飞越要覆盖的区域，并在垂直于给定扫描方向的行中来回运动。为找到给定多边形的最佳覆盖方向，可使多边形在平面内绕水平轴旋转，并测量其高度。最佳方向是产生最小高度hmin的方向。一旦找到最佳扫描方向，就可在该区域规划航迹。假设图像传感器平行于地平面，已知图像传感器的宽度l，相机镜头的焦距为f，均以mm 为单位，相机到地面的距离H（飞行高度），单位为m，则相机在地面上的覆盖宽度（m）

覆盖行数

式中，α∈（0，1）为两幅图像之间的重叠比例，这种重叠通常是连接图像以组成航空地图所必需的。

飞行线之间的距离

对于固定翼无人机，还须考虑其最小转弯半径

式中：v为无人机飞行速度；g为重力加速度；φmax为无人机最大滚转角。

1.3 边-点路径构建

为构建边-点路径，通过迭代将线Lflight与多边形相交将航点添加到航迹中（见算法1）。该算法需要输入多边形、初始顶点b，相邻顶点bmate，顶点b的对映顶点a以及飞行线之间的距离dx。对于固定翼无人机，取dx=2Rmin。首先，创建一条Lflight，平行于边（b，bmate），其垂直于扫描方向且位移一个偏移量Δinit=d/2（见图2）。Lflight与多边形相交，得到点ip1和ip2，通过CheckAndConnect函数建立垂直约束，并按照正确的顺序连接起来以形成无人机的航线，对于固定翼无人机来说，这有利于杜宾曲线的构建。不断将直线向a方向移动并与多边形相交，最后算法返回航迹ρ=｛p0，…，pm｝。构造的边-点路径从b开始到bmate，并扫向a。如果航迹包含起飞点和着陆点，则可表示为：τ=｛ps，p0，…，pm，pe｝。

算法1获取多边形的边-顶点路径（GetPath（b，bmate，a））。该算法计算多边形Q=｛V，E｝的来回路径（ρ=｛p0，p1，…，pm｝）。路径从初始顶点b开始，指向bmate，然后扫向a。

输入：Q，d，b，bmate，a

输出：ρ

1. Δinit= d/2；

2. Lflight←GenerateLine（b，bmate）；

3. Lflight←OffSet（Lflight，Δinit）；

4. ρ ←Ø；

5. while Intersects（C（Lflight），Q）do

6. ip1，ip2←IntersectEdges（Lflight，E）；

7. ρ ←CheckAndConnect（ρ，ip1，ip2）；

8. Lflight←OffSet（Lflight，d）；

9. return ρ；

2 改进的旋转卡尺航迹规划

2.1 算法简介

改进的旋转卡尺航迹规划总体流程如图3 所示，该算法对固定翼无人机和多旋翼无人机均适用，路径规划开始时，输入RoI的顶点坐标，算法根据RoI是否为凸多边形而作相应处理，如果是凸多边形，则对凸多边形作旋转卡尺航迹规划。如果是凹多边形则先将RoI分割成最少个数的凸多边形［21］，再对子区域做旋转卡尺航迹规划。在得到航点后，如果无人机是固定翼的，则标记相应转弯航点，以便将算法应用于实际时，对转弯航迹进行离散化处理后上传至飞控。

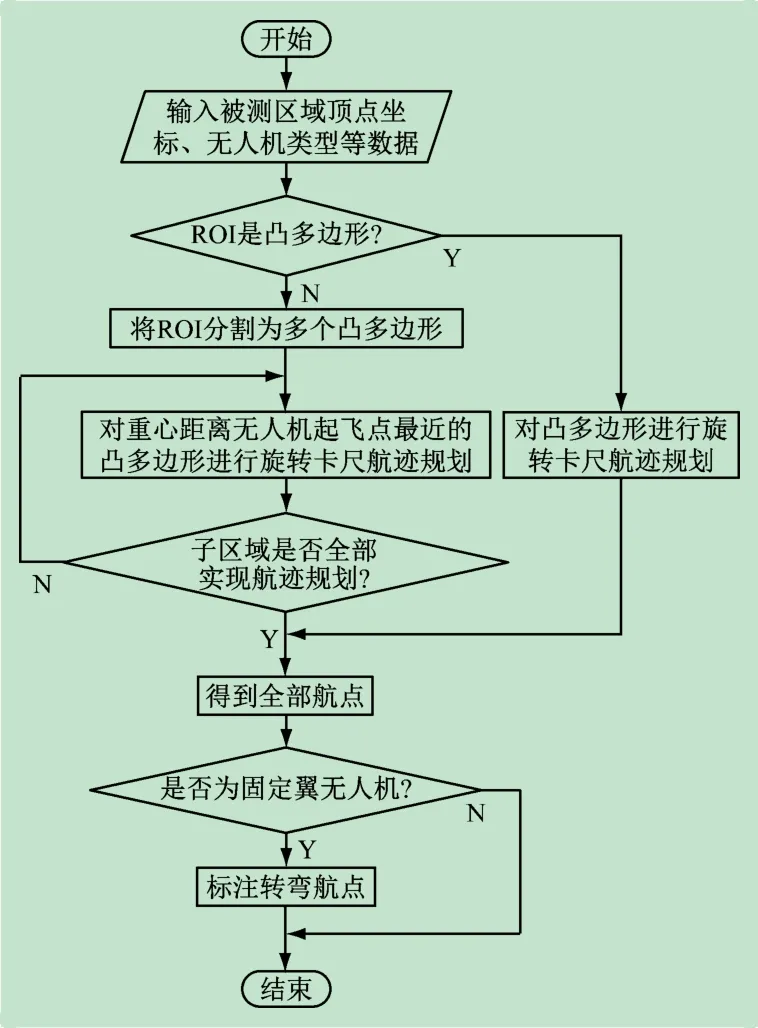
图3 算法总体流程图

2.2 航迹规划

2.2.1 对映点对计算

考虑任务起止点，采用旋转卡尺航迹规划［20］来得到覆盖RoI的航迹。建立覆盖RoI的来回搜索模式，以找到结合起点和终点的最少路径。如果不考虑任务的起点和终点，那么最优路径是飞行线垂直于最小宽度的路径。一般来说，为解决这个问题，必须测试具有起点和终点的来回路径的所有可能组合。发现所有来回路径的覆盖都始于和终于对映点对，对映点对的数量被限制在x=（3/2）·n。若已知一组给定对映点对的最优路径，则与起点和终点的组合也能计算出来。算法2 为旋转卡尺航迹规划，第1 行ComputeAntipodalPairs函数用于获得对映点对集，输入为顶点集V，返回凸多边形的对映点对集，即A=｛（i1，j1），（i2，j2），…，（in，jn）｝，在O（n）时间内计算所有对映点对，其中n是多边形的顶点数。对于每组对映点对（第3 行），计算最优路径（第4 行），并将其附加到起点和终点（第5 行）。BestPath（）函数将在2.2.2 节中解释。由于路径的顺序很重要，按照正序和逆序进行测试，并选择距离最小的路径（第5 行）。如果当前路径的代价更小，则将其保留为最优完整航迹（τ）。最后，一旦测试完所有的对映点对，返回τ。

算法2旋转卡尺航迹规划。得到包含起点ps，边-点路径ρ和终点pe的完全航迹τ。

输入：V，ps，pe

输出：τ

1. A ←ComputeAntipodalPairs（V）；

2. c*←∞

3. foreach（i，j）∈A do

4. ρ ←BestPath（V，i，j）；

5. τaux←minCost（｛ps，ρ，pe｝，｛pe，ρ，ps｝）；

6. if cost（τaux）＜c*then

7. τ ←τaux；

8. c*←cost（τ）；

9. return τ；

2.2.2 计算每组对映点对的最优航迹

计算对映点对i和j的最优来回航迹，参见算法3。其主要思想是找到通过顶点i和j的一组平行线，它们之间的距离最小，然后得到与这些线匹配的来回航迹。该过程给出一组对映点对和一个接触该对的卡尺，顺时针旋转卡尺，直到和边接触并测量多边形的高度，然后逆时针旋转卡尺，直到第2 条边接触并测量高度，最后，比较2 个高度以找到最小高度。假设n个顶点从0 到n-1 标号，angle（m，n）函数用于计算一条直线从平行于边（m，m+1）的位置顺时针旋转到平行于边（n，n+1）的位置时所掠出的角度。

算法3BestPath（V，i，j）函数计算对映点对的最优航迹ρ，输入为边集V和对映点对（i，j）。

输入：V=｛1，2，…，n｝，（i，j）

输出：ρ

/*顺时针旋转卡尺*/

1.if angle（i，j）-π ＜0 then

2. b ←j；

3. a ←i；

4. else

5. b ←i；

6. a ←j；

/*逆时针旋转卡尺*/

7. φ←angle（b，a）-π；

8. γb←angle（b-1，b）；

9. γa←angle（a-1，a）-φ；

10. if γb＜γathen

11. b2←b-1；

12. a2←a；

13. else

14. b2←a-1；

15. a2←b；

/*寻找航线最少的路径*/

16. if dist（b，a）＜dist（b2，a2）then

17. ρ ←GetPath（b，b+1，a）；

18. else

19. ρ ←GetPath（b2+1，b2，a2）；

首先，顺时针旋转卡尺，找到接触的第一条边，以（b，b+1）表示并且它将是一条可能的BFP 的基边。以图4 为例，如果在对映点i和j上旋转直线L和M，第一条接触边将是（j，j+1），其与M′相重合。找到边（b，b+1）的一种方法是找到αi和αj两者的较小角度，即从假想的支撑线顺时针方向旋转到多边形最近边的角度。通过测量从线L′到线M′旋转的差值而非测量αi和αj确定基边，参见算法3 的第1 ～6 行。如果角度减去π的差小于零，则边（j，j+1）被视为航迹的基边。否则，将边（i，i+1）作为基边。一种特殊情况是两个角度相等，在这种情况下，航线的数量是相同的，就航线数量而言，选择哪个基边并不重要。为使算法简单，在角度相等的情况下，选择边（i，i+1）作为基边。一旦找到边（b，b+1），就将其存储为第一个可能的基边。

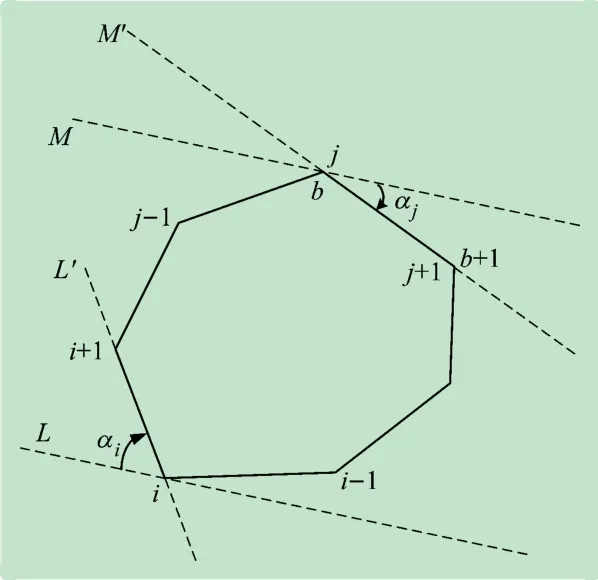
图4 卡尺顺时针旋转示意图

逆时针方向旋转卡尺以找到另一条可能的航迹，基边为（b2，b2+1）。从嵌入式系统角度考虑，采用同一个angle（）函数，基于此，测量相对于直线B的角度，直线B与（b，b+1）重合（见图5）。角γb即边（b-1，b）和直线B之间的角度。角γa为边（a-1，a）和直线A之间的角度，直线A为经过a点的直线B的平行线。角φ与角γa互补以到达边（a，a+1）、边（b，b+1）在边（a，a+1）之前接触卡尺，因此角φ大于或等于0。角γb和γa的较小值决定两种可能性中的边：（b-1，b）或（a-1，a）。一旦确定则第2 个基边（b2，b2+1）就找到了，则最远的顶点就是对映点对，参见算法3 第7 ～15 行。

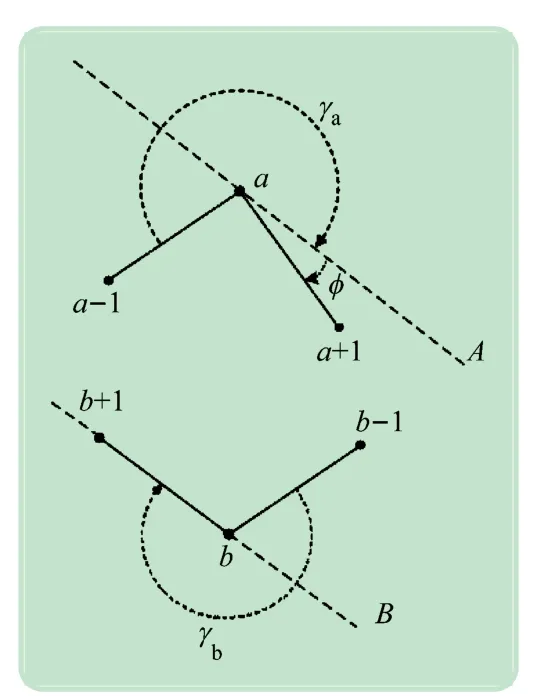
图5 卡尺最后位置与之前多边形边之间的角度

现有2 种可能的航迹：一条以（b，b+1）为基边的航迹，在顶点a处结束；另一条以（b2，b2+1）为基边的航迹，在顶点a2处结束。选择飞行路线最少的路径，参见算法3 的第16 ～19 行，其中函数dist（b，a）计算与边（b，b+1）重合的直线与顶点a之间的距离，函数getPath（b，bmate，a）计算原点位于顶点b的BFP，扫描方向垂直于（b，bmate）。

3 实验结果与分析

对本文所提改进的旋转卡尺路径规划（IRCPP）用Matlab仿真，并和文献［20］中的RCPP对比，无人机飞行参数如下：无人机飞行速度，v=5 m·s-1，航距，dx=20 m，无人机飞行高度，H=50 m，无人机最小转弯半径，Rmin=10 m。

IRCPP与RCPP比较结果如图6 所示。图6（a）、（b）分别为IRCPP 和RCPP 对于凸多边形ROI 时，无人机分别为固定翼和多旋翼时的仿真。当无人机为固定翼时，RCPP并不适用，而IRCPP可根据无人机的类型作出相应的航迹规划。图6（c）、（d）分别为IRCPP和RCPP对于凹多边形RoI 时，无人机分别为固定翼和多旋翼时的仿真。IRCPP首先进行凹多边形区域凸分解，然后再做规划，而RCPP 对于凹多边形ROI，虽然也能完成航迹规划，但对于具有狭长区域的地形，其转弯次数多于IRCPP，如图6（c）、（d）所示，IRCPP 转弯17 次，RCPP转弯21 次。

图6 两种算法在固定翼和多旋翼无人机路径规划中的比较

综上，RCPP 只适合于ROI 是凸多边形的多旋翼无人机航迹规划，而IRCPP可根据ROI的形状和无人机类型作出相应的航迹规划，更具实用性。

4 结语

改进的旋转卡尺路径规划算法考虑被测区域的凹凸性，如果被测区域是凹多边形，则先将其分割为具有最少个数的凸边形，使算法更具实用性。将无人机飞行起点和着陆点包括在内，计算最优边-点来回航迹，构成完整覆盖航迹，更符合实际应用场景，算法复杂度为O（n），其中n为感兴趣区域的边数。考虑无人机类型，如果是固定翼无人机，则需考虑其最小转弯半径，使算法更具适用性。实验仿真表明了算法的实用性和适用性。

·名人名言·

我们应该不虚度一生，应该能够说，“我已经做了我能做的事。”

——居里夫人