非线性损伤模型的载荷谱设计与试验验证
2023-10-26魏国前何文波闫梦煜
魏国前, 何文波, 闫梦煜, 赵 刚
(武汉科技大学a.冶金装备及其控制教育部重点实验室;b.机械传动与制造工程湖北省重点实验室;c.精密制造研究院,武汉 430081)
0 引言
疲劳断口是疲劳试验的重要产物之一,包含了丰富的疲劳演化线索,是记录疲劳裂纹形成和发展过程的直接证据[1]。海滩条带是疲劳断口中最重要的宏观形貌特征,真实体现了裂纹前沿的形状和演化过程,可以有效判断裂纹萌生位置和扩展路径[2]。
受试件材料和载荷形式的影响,不是所有的疲劳断口都会产生海滩条带,试验环境下一般需要特殊手段才能生成可识别的海滩条带。最常使用的方法是勾线法[3-5],即在基线载荷谱块之中插入具有不同应力水平的标记载荷谱块。标记载荷谱块既要求能够产生足够的疲劳损伤,以便在疲劳断口上形成肉眼可识别的条带宽度,同时又要求损伤占比小,不至于影响最终的试验寿命值。因此,需要设计合理的疲劳载荷谱,并对其中标记载荷谱块可能导致的疲劳损伤进行估算与分析。
通常采用Miner 线性损伤累积理论估算疲劳损伤,该理论无法计及载荷次序对变幅疲劳损伤的影响[6]。试验研究表明,“高-低”和“低-高”的2 级载荷谱具有不同的损伤特性,不同加载次序的多级载荷谱则会产生更为复杂的损伤行为,需要采用精度更高的非线性损伤累积模型[7-8]。目前已经出现许多非线性损伤累积模型[9-11],其中M-H非线性损伤累积模型需要的材料参数较少,预测精度较高,获得了较为广泛的应用[12-13]。
本文拟针对承受循环拉伸载荷的十字焊接接头,设计多种具有不同标记载荷谱块的疲劳载荷谱,基于M-H非线性损伤累积模型估算并分析标记载荷谱块的损伤特性,选出较优的疲劳载荷谱设计方案,并开展相应的疲劳试验,验证上述方法及所提疲劳载荷谱的合理性和有效性。
1 理论基础
1.1 海滩条带生成原理
通过合理设计疲劳载荷谱生成海滩条带的基本原理如图1 所示。以2 级载荷谱为例,其中的基线载荷谱块具有较大的应力水平,对疲劳损伤起主要作用。在基线载荷谱块之中间断地插入若干个具有不同应力水平的标记载荷谱块。由于标记载荷谱块与基线载荷谱块的应力水平存在明显差异,造成的疲劳损伤程度和失效速率明显不同,在疲劳断口上显现为明暗亮度不同且肉眼可辨的失效区域。通常,标记载荷谱块造成的疲劳损伤较小,对应的失效区域较为狭窄,往往呈现为条带状,因此被称为海滩条带。可见,标记载荷谱块的参数对海滩条带的最终形态具有直接影响。
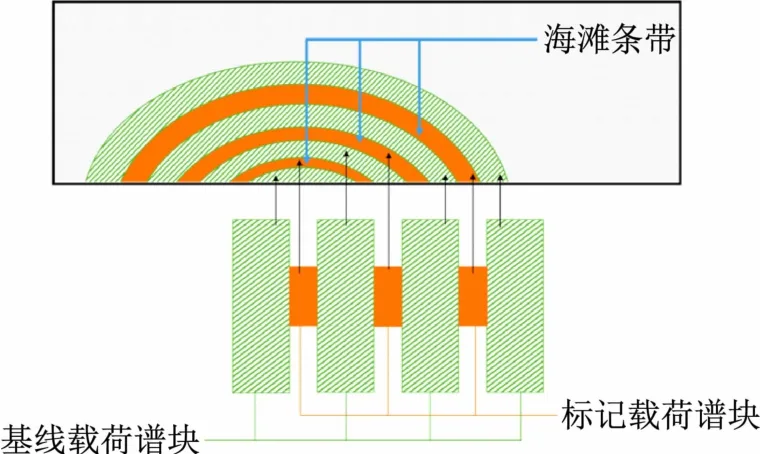
图1 海滩条带生成原理示意图
一般而言,标记载荷谱块的数量与海滩条带的数量是一致的。由于疲劳损伤过程具有高度的非线性,早期阶段的标记载荷谱块引起的疲劳损伤远远小于相同参数的标记载荷谱块在后期阶段引起的疲劳损伤,导致早期阶段的海滩条带过于狭窄而较难辨认,而后期阶段的海滩条带则过于粗大而不利于裂纹扩展行为的精确定量分析。从疲劳试验目的来看,基线载荷谱块对应的循环加载次数更符合疲劳寿命在物理意义的概念内涵。如果标记载荷谱块产生的疲劳损伤较小,固然不会影响最终的试验寿命,但也不易生成满意的海滩条带;疲劳损伤过大,则很可能显著影响试件的疲劳失效行为,带来不可接受的试验寿命误差。此外,如果采用增加标记载荷谱块循环次数的方法增大疲劳损伤,还会急剧增加试验时长,加重试验成本和负担。
由上可知,海滩条带与标记载荷谱块的疲劳损伤紧密相关。为了设计合理、可靠的疲劳载荷谱,必须对其中不同载荷谱块的疲劳损伤进行有效的定量估算。
1.2 M-H非线性损伤累积模型
针对疲劳损伤过程,目前已经有较多成熟的损伤累积模型,对于变幅载荷,常常采用非线性模型。本文采用M-H非线性损伤累积模型,其疲劳损伤定义可描述如下[12-13]:
式中:D为疲劳损伤;n为循环加载次数;Nf为达到最终失效的总循环加载次数(即疲劳寿命);a0为用于表征损伤初始状态特征缺陷尺寸的参量,一般取0.18 mm。
给定一个应力水平,则可根据材料的S-N 曲线获得对应的疲劳寿命,进一步可以根据式(1)绘制D与n之间的关系曲线,描述D随n的非线性演化行为,如图2 所示。
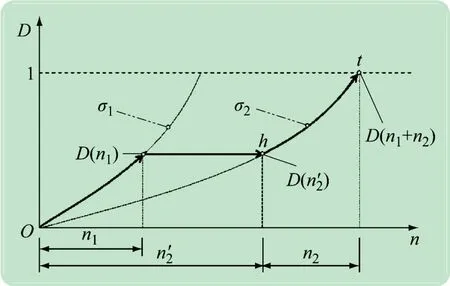
图2 疲劳损伤曲线
借助图2 的损伤曲线,可以方便地分析多级疲劳载荷谱的损伤演变过程。以2 级载荷谱为例,假设应力水平分别为σ1和σ2,材料在σ1下首先加载n1次,则由式(1)可以计算得到第1 级载荷谱块结束时的累积损伤
式中,Nf1为对应σ1的疲劳寿命。
此时,D状态对应图2 中k点,该点位于对应于σ1的损伤曲线上。在此基础上进入第2 级载荷谱块,考虑到此时材料已经具有一定的损伤,因此需将D状态点由k点平移至对应σ2的损伤曲线之上,即图2 所示h点。假设该点的损伤完全由对应σ2的损伤曲线演化产生,则累积损伤由下式计算:
式中:Nf2为对应σ2的疲劳寿命;n2′为第1 级载荷谱块产生的D对应第2 级载荷谱块应力水平的等效循环次数。联立式(2)和(3),可计算获得等效循环次数:
第2 级载荷谱块结束时,材料发生的D状态对应图2 中的t点,相应的累积损伤由下式计算:
通常,针对i级疲劳载荷谱,疲劳损伤累积模型可描述为:
式中:ni为第i级载荷谱块的循环加载次数;Nfi为对应第i级载荷谱块应力水平σi的疲劳寿命;αi-1,i为寿命比特征指数,可由下式计算:
2 疲劳载荷谱设计
2.1 载荷谱的描述
本文针对十字焊接接头开展拉伸疲劳试验,试件几何构造如图3 所示。根据BS7608 疲劳规范[14],该试件符合F类别焊接接头构造,对应的S-N 曲线表达式为:
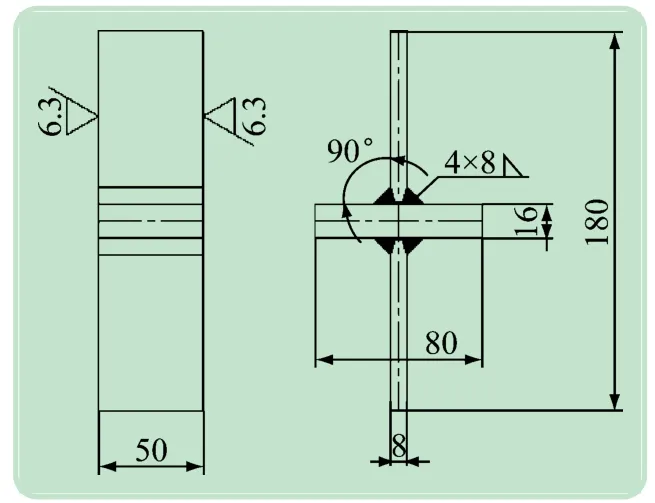
图3 十字焊接接头几何构造(mm)
式中:ΔS为应力变程;N为疲劳寿命;m与C分别为与试件材料、加载方式有关的参数,参考BS7608 疲劳设计标准中的F构造类别,取m=3,C=4.7167 ×1012。
按照2 级载荷谱块的形式设计疲劳试验载荷谱,其中,基线载荷谱块的应力水平设为0 ~200 MPa,按照式(8)可初步估算其寿命约为100 万次。结合已有的试验经验,将首次基线载荷谱块的n设置为30 万次,之后的基线载荷谱块的n设为10 万次。为标记载荷谱块设置不同的ΔS、平均应力Sm和n,具体组合方案如表1 所示,其中包括4 种ΔS:40、80、100、120 MPa,4 种Sm:60、80、100、120 MPa,以及2 种n:5、10万次,共计32 种组合。
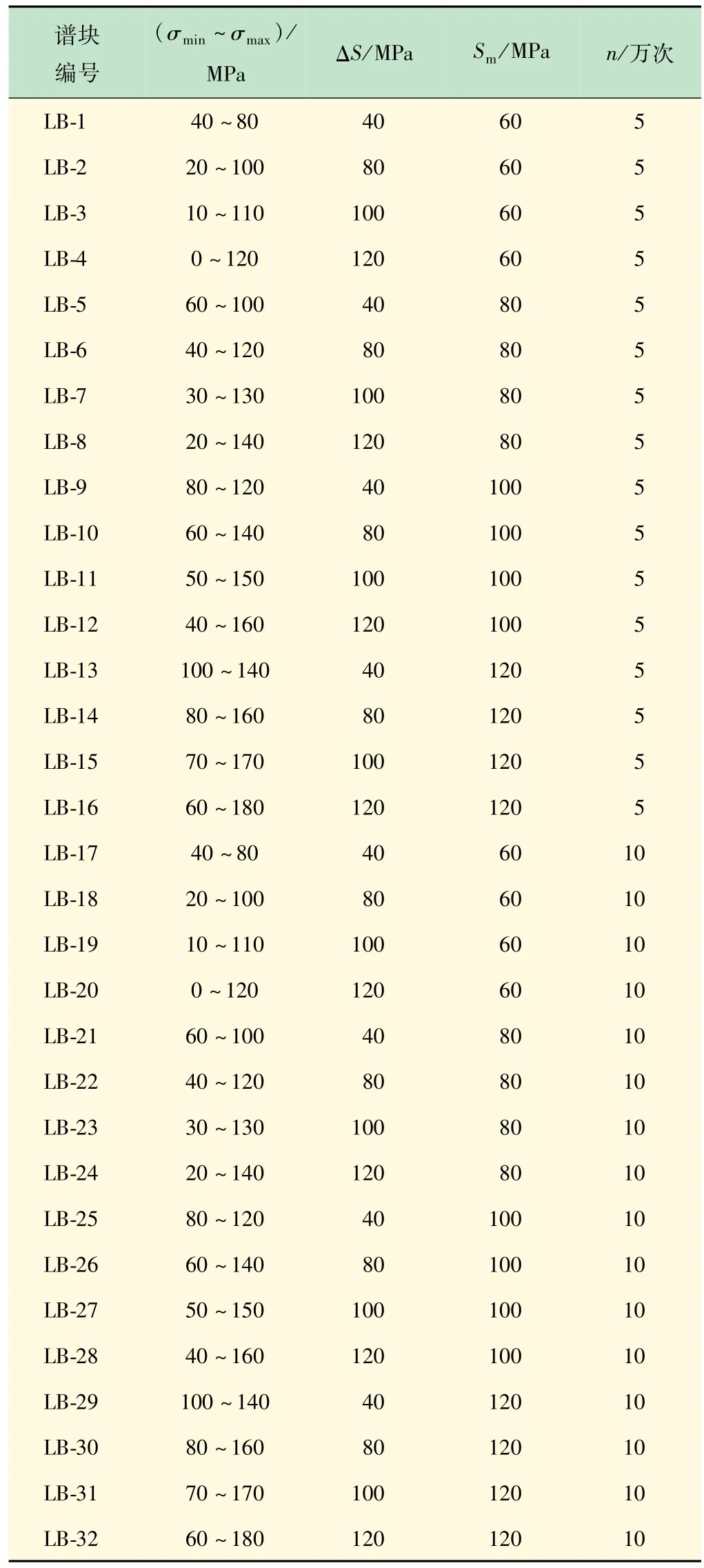
表1 标记载荷谱块的设计参数
2.2 损伤与寿命估算
采用M-H非线性损伤累积模型估算表1 中各个疲劳载荷谱的D,其中基于Goodman方程考虑了Sm的影响。计算结果如表2 所示,其中估算寿命对应的D=1。由表可见,几乎所有设计载荷谱的基线载荷谱块产生的D均显著高于标记载荷谱块产生的D,表明标记载荷谱块对试件疲劳性能几乎没有影响。
此外,所有基线载荷谱块产生的D均相同,而标记载荷谱块产生的损伤则有明显差异,这种差异对海滩条带的生成效果有直接影响。一般来看,ΔS、Sm和n对损伤均有影响,其中ΔS的影响最为突出,n的影响几乎可以忽略。可以认为,标记载荷谱块的ΔS是影响海滩条带的主要因素。
本质上,ΔS越大,D值越大,对断口表面形貌的作用将更加明显。如果将标记载荷谱块的ΔS设置得过大,甚至接近基准载荷谱块的ΔS,则会导致2 种载荷谱块生成的断口形貌趋同,不利于海滩条带的表面形貌区分。另一方面,如果将标记载荷谱块的ΔS设置得太小,在相同n下对应的D值则会很小,导致无法驱动裂纹前沿向前扩展肉眼可见的距离。结合上述两方面因素,以block-4 为基准,将D由小到大排序,然后选取中间的7 个设计载荷谱,如表2 中粗体所示。可以发现,这些设计载荷谱的临界损伤状态均发生在第7 个载荷谱块之中,即对应第4 个基线载荷谱块,理论上可以产生3 条海滩条带。在这7 个设计载荷谱中,剔除标记载荷谱块n=10 万次的LB-18 和LB-22。同时考虑应力水平的多样性及估算寿命尽可能小等因素,最终确定LB-4、LB-11、LB-14 等3 种载荷谱为试验载荷谱。拟针对该3 种试验载荷谱各开展3 根接头的疲劳试验,共计9 根试件。
3 试验验证
3.1 试验描述
根据图3 所示的十字焊接接头构造形式和尺寸制造9 根试件,依次标记为C1 ~C9。试件母材采用低合金结构钢Q345,焊条采用CHW-50C6,依照相关标准预制切口以确保全熔透焊接,焊后采用锤击法消除残余应力。在长春SDS100 疲劳试验机上开展疲劳试验,试验机的最大载荷为80 kN。按表1 中LB-4(试件为C1 ~C3)、LB-11(试件为C4 ~C6)、LB-14(试件为C7 ~C9)等3 种载荷谱进行实际加载。加载频率设为10 Hz,试验终止条件设为总n为200 万次或位移保护值为4 mm。
3.2 结果与分析
共有8 根试件发生疲劳断裂,另有1 根试件(C7)由于电脑故障而中途终止试验。为了确保试验条件的一致性,之后未继续试验。发生断裂的8 根试件中,所有裂纹均萌生于薄板焊趾部位,其中6 根试件在疲劳断口生成了较为清晰的海滩条带。另外2 根(C6 和C8)的海滩条带较难辨认,应该与试件材料和焊接质量的分散性有关,这也进一步说明海滩条带影响因素的多样性和随机性。
图4 所示为C2 试件的疲劳断口照片。由图可见,有3 个明显的裂纹。裂纹1 萌生于试件边缘,以角裂纹形式独自扩展;裂纹2 和3 萌生于试件中部区域,首先以表面裂纹形式独自扩展,随后发生融合并一同扩展。通过体式显微镜观察各个裂纹的局部细节,可以在裂纹3 的内部看到3 条清晰的海滩条带。相较之下,裂纹1 和2 内部的海滩条带较为模糊,但借助一些断续、支离的形貌线索,也能判断相应海滩条带的大致位置,如图中红色虚线所示。C2 试件完全断裂时的循环加载次数(后文定义为试验寿命)为69.41 万次,期间经历了3 次标记载荷谱块,对应断口的3 条海滩条带,表明该试件的疲劳载荷谱设计是合理、有效的。此外,借助海滩条带可以清晰地看到焊接接头发生疲劳破坏时的多裂纹现象,也能够直观地分析多裂纹的扩展细节特征,这进一步表明海滩条带对焊接结构疲劳断口宏观分析的重要性。
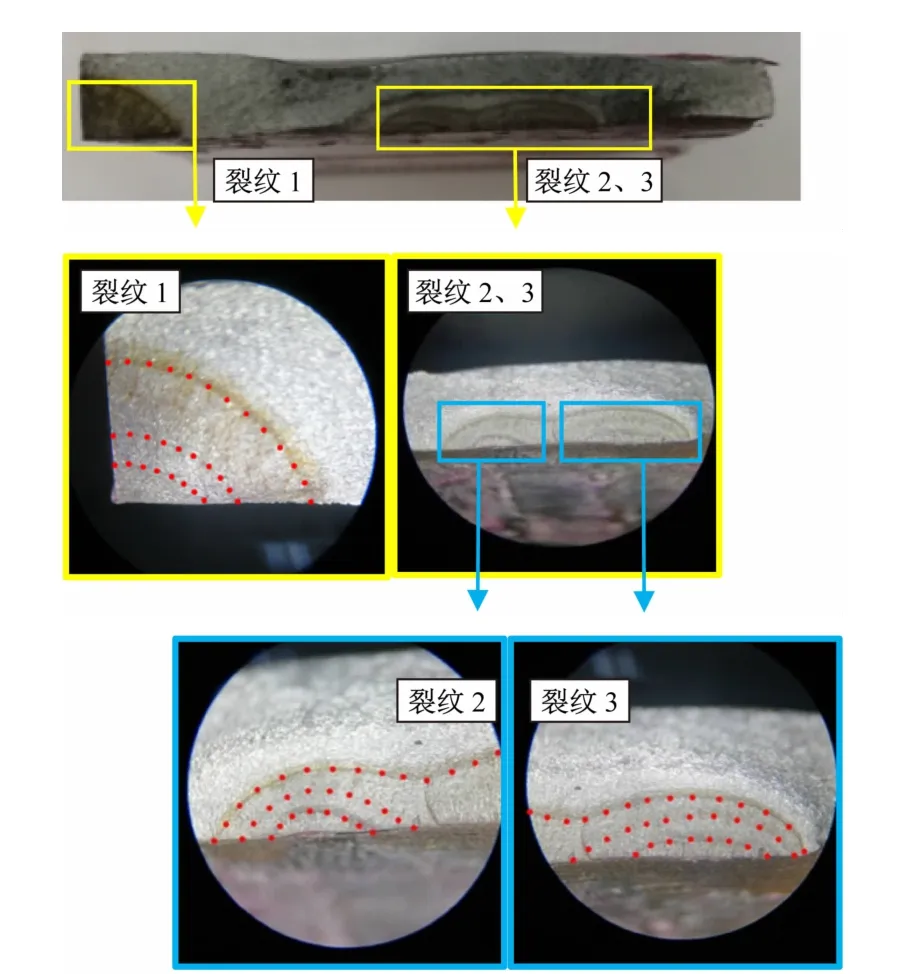
图4 试件C2疲劳断口照片
整理所有试件的试验寿命,同时基于疲劳损伤累积模型计算所有设计载荷谱的估算寿命及其相对误差,如表3 所示,其中相对误差以试验寿命平均值为基准。为便于比较,表3 中同时列入了M-H非线性损伤累积模型和Miner线性损伤累积模型的估算结果。可以看出,2 种模型的估算寿命与试验寿命平均值相比均具有较高的精度,相对误差均小于10%。相较之下,M-H模型精度更高。值得注意,表3 中的试验寿命显示,试件C6 的破坏发生在第4 个标记载荷谱块期间,试件C8 的破坏发生在第5 个基线载荷谱块期间,即试件C8 经历了完整的第4 个标记载荷谱块。然而,试件C6 的疲劳断口只发现了3 条海滩条带,这可能是由于第4 个标记载荷谱块已经接近疲劳过程的后期阶段,损伤行为过于剧烈和不稳所致。试件C8 的疲劳断口则没有发现可辨认的海滩条带,应该与疲劳试验分散性有关。
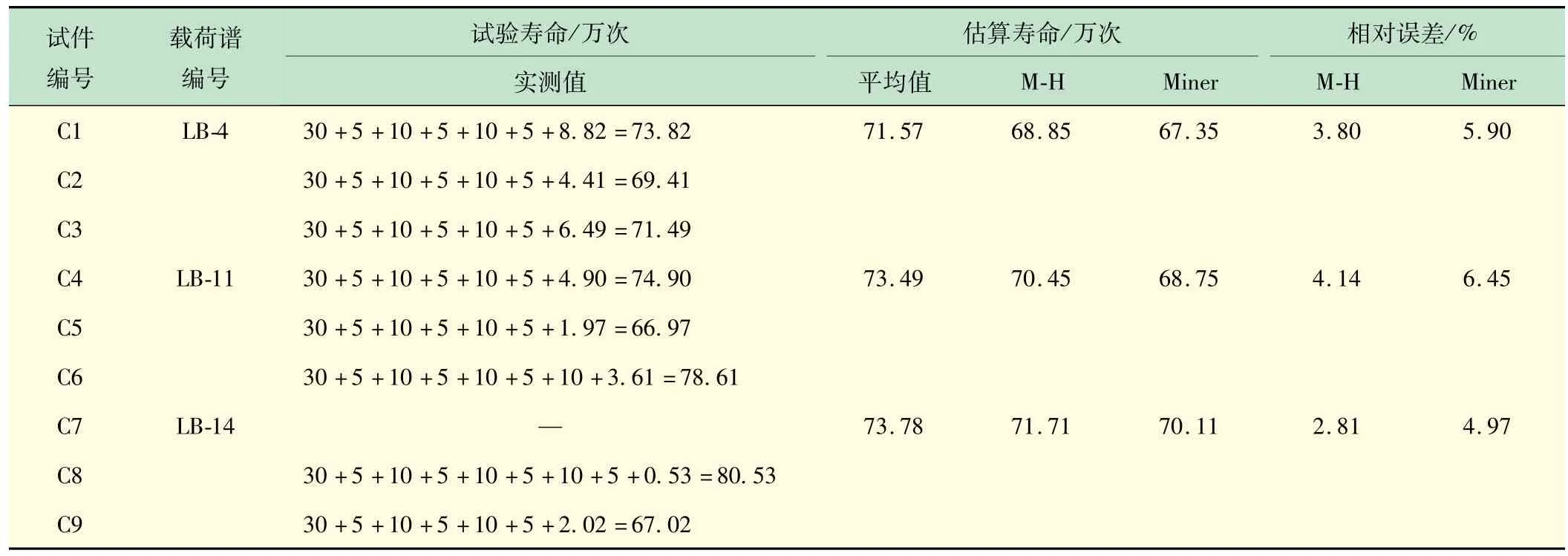
表3 试验寿命与估算寿命对比
采用误差散射图对表3 中各个试件的试验寿命和估算寿命进行比较,如图5 所示。可以看出,如果以单个试件的试验寿命为基准,大多数估算点位于±10%散射带之间,少数位于-25% ~-10%散射带之间。对于单个试件而言,绝大多数基于M-H模型的估算点都更靠近对角线,表明M-H模型的寿命预测精度优于Miner模型,这说明非线性损伤累积模型在变幅载荷疲劳寿命预测方面更具优势。
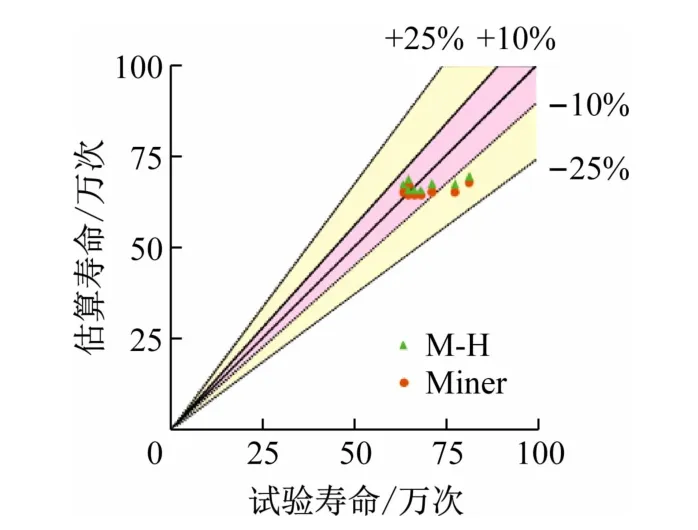
图5 试验与估算寿命的比较
4 结语
本文研究了基于M-H 非线性损伤模型的疲劳载荷谱设计方法,并进行了9 根十字焊接接头试件的变幅载荷疲劳试验,结果表明:
(1)6 根试件在疲劳断口生成了较为清晰的海滩条带,非线性损伤模型在分析与设计疲劳载荷谱方面具有合理性和可行性。
(2)针对32 组标记载荷谱块的损伤估算表明,ΔS对海滩条带生成效果的影响最大,在疲劳载荷谱设计中应予以重点考虑;n的影响最小,且会显著增加试验总时长,加重试验成本,设计疲劳载荷谱的时候可不予考虑。
本文所提方法对疲劳试验载荷谱设计以及海滩条带的生成技术具有指导意义。
·名人名言·
实验室和发明是两个有密切关系的名词,没有实验室,自然科学就会枯萎;科学家一经离开了实验室,就变成战场上缴了械的战士。
——巴斯德
