复杂载荷简化对梁内力和变形的影响

李银山， 薛春霞， 韩 蕾， 李尚志， 叶红玲

（1.河北工业大学机械工程学院，天津 300401；2.海南大学土木建筑工程学院，海口 570228；3.山东工程职业技术大学建筑工程学院，济南 250200；4.北京航空航天大学数学科学学院，北京 100191；5.北京工业大学材料与制造学部，北京 100124）

0 引言

钢筋混凝土简支板桥是小跨度桥梁最常用的结构形式之一，在国内外被广泛地使用于中小城市的公路主干线上，在城市交通中发挥着重要作用。因此简支梁力学模型是教学中最常使用的力学简化模型之一［1］。针对梁的弯曲变形，研究者提出了多种方法［2-4］。如奇异函数法可以很简洁地获得整根阶梯形梁的挠度方程［5］，并推广应用于多层框架结构［6］。但应用函数表达的挠度形式复杂。林金木［7］提出了一种新方法推导出梁在任意荷载下的挠度曲线表达式。李彤等［8-9］对三铰拱桥结构的静力分析和影响线进行了研究。积分法是基本的计算方法，其优越性在于可用解析方法得到挠度方程和转角方程，求解平面弯曲梁的挠度和转角，可用载荷方程积分法［10］，需要对挠度的挠曲线近似微分方程进行4 次积分运算并结合边界条件才能得到挠度。对于简单的线性分布载荷表达式，可由载荷方程积分法获得弯曲变形的精确解，但是，对于表达式复杂的非线性分布载荷，由于函数表达式的不可积，很难得到它的精确解［11］。李银山［12］提出的连续分段独立一体化积分法是一种快速求解结构弯曲变形问题的解析方法，求解了复杂载荷作用下变刚度超静定梁弯曲变形的解析解［13］。

本文利用连续分段独立一体化积分法求解复杂载荷作用下简支梁的弯曲变形解析解。针对复杂的非线性分布载荷表达式，首先利用函数的泰勒级数展开法，分别选取前4 项，将复杂分布载荷简化成均布载荷、线性分布载荷、抛物线分布载荷和三次多项式分布载荷。再将梁进行连续分段离散化，按等步长分成m等分，并利用最小二乘法回归成n次多项式，分别求解梁的内力和变形，并进行相对误差计算和其对各多项式系数灵敏度分析。

1 问题的提出

图1 所示为承受复杂载荷的简支梁，设长为L、抗弯刚度为EI的简支梁，承受分布载荷q（x），集中载荷F和集中力偶Me。作用在梁上的分布载荷

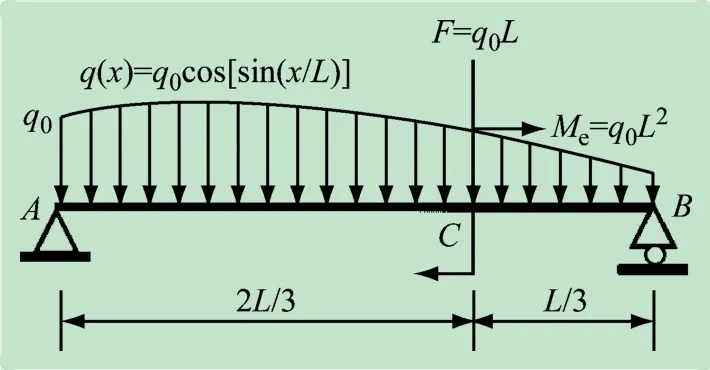
图1 承受复杂载荷的简支梁

求解梁的内力与变形。式中：x为距离原点A的位置；q0为最大值。

复杂分布力最大值

简支梁的挠曲线微分方程为

式中：v为挠度；EI为梁的弯曲刚度。

边界条件为：

为了便于编程计算，引入变量：

并定义：

同时，将方程式（3）无量纲化，并将式（1）代入可得：

边界条件为：

由于任意函数f（X）可以展开为X的泰勒级数［14-15］，可得

将式（7）离散化，按等步长将梁分成m等分，利用最小二乘法回归成n次多项式。n次多项式系数，原函数式（9）离散化等分数m与分布载荷相对误差对照表见表1 和表2 所示。相对误差为

表1 分布载荷函数离散化等分数、多项式系数对照表

表2 分布载荷函数离散化等分数与相对误差对照表%

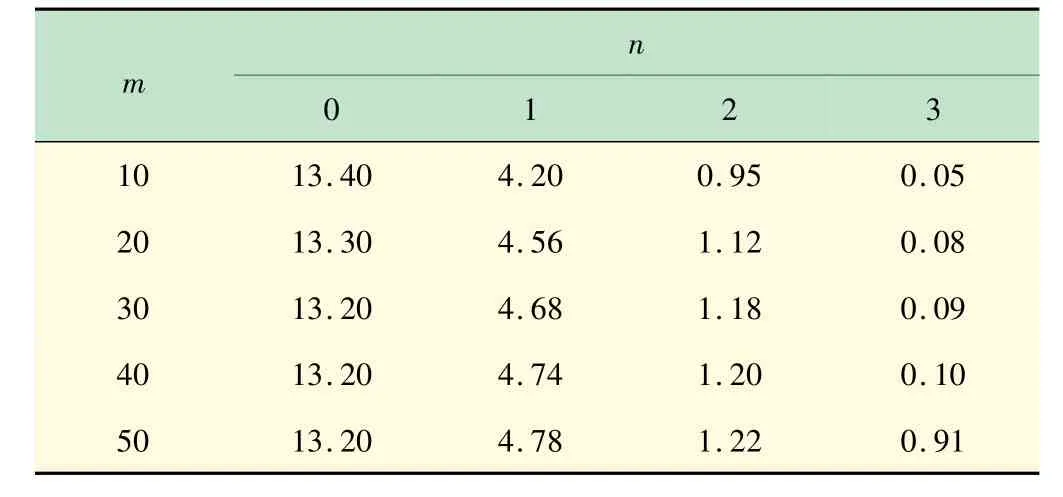
表2 分布载荷函数离散化等分数与相对误差对照表%

n m 01 23 1013.404.200.950.0520 13.304.561.120.0830 13.204.681.180.0940 13.204.741.200.1050 13.204.781.220.91

2 复杂分布载荷的简化（以m=20 为例）

2.1 将复杂分布载荷简化成均布载荷

工程中经常将分布载荷简化成均布载荷，如图2所示。在式（9）中的展开式只取常数项（n=0），即：

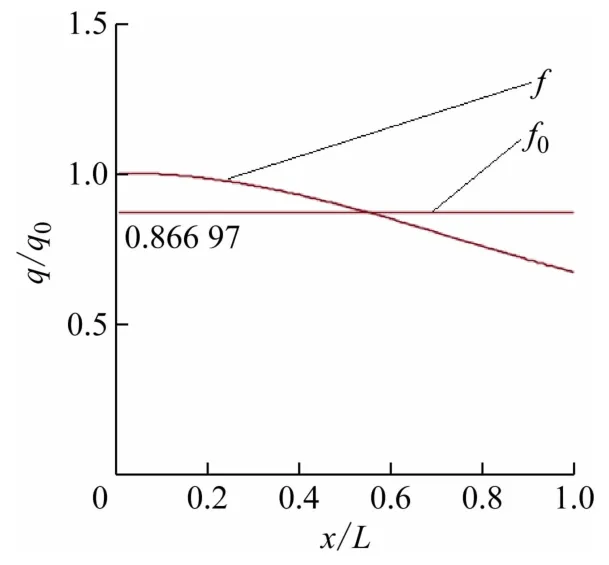
图2 均布荷载与原分布荷载

将梁分成两段k=2，简支梁的挠曲线微分方程为：

其边界条件和连续光滑条件为：

用连续分段独立一体化积分法求解，得到：

（1）剪力函数

（2）弯矩函数

（3）转角函数

（4）挠度函数

n=0 时，对应简支梁的内力和变形，如图3 所示。

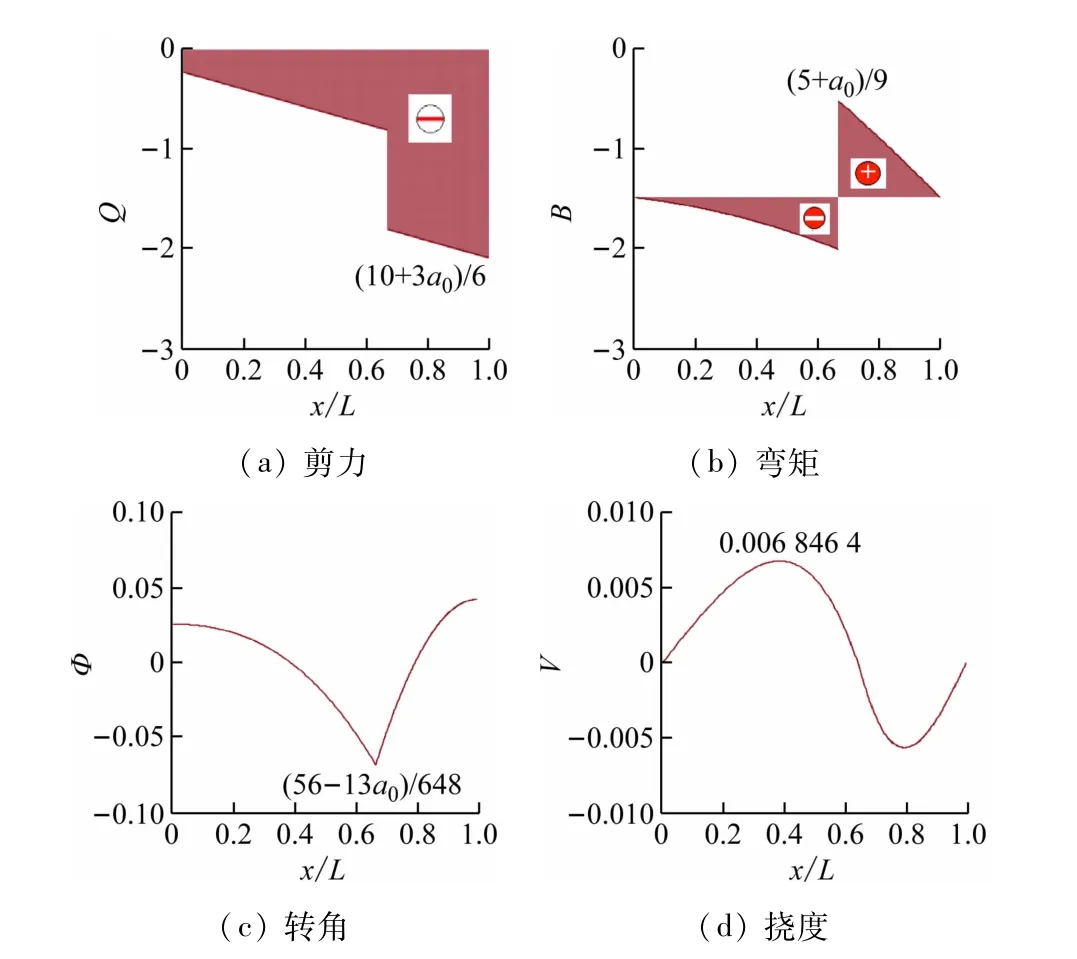
图3 n=0时简支梁的内力和变形图

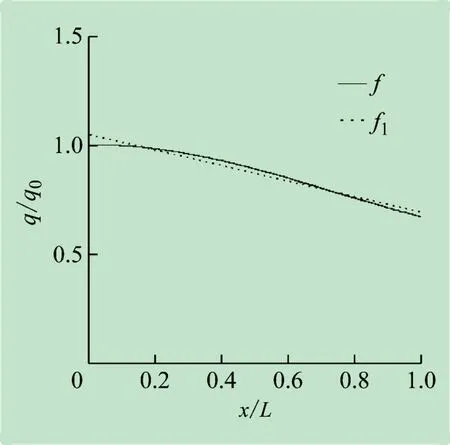
图4 线性分布荷载与原分布荷载

由此，得到的最大剪力、最大弯矩、最大转角及最大挠度分别为：

2.2 将复杂分布载荷简化成线性分布载荷

工程中经常将分布载荷简化成线性分布载荷如图4 所示，即在式（9）中的展开式中只取一次函数（n=1），即

利用最小二乘法解得：a0=1.0456，a1= -0.35722。可得分布力最大值：

用同样方法得到n=1 时，对应简支梁的内力图和变形图如图5 所示。

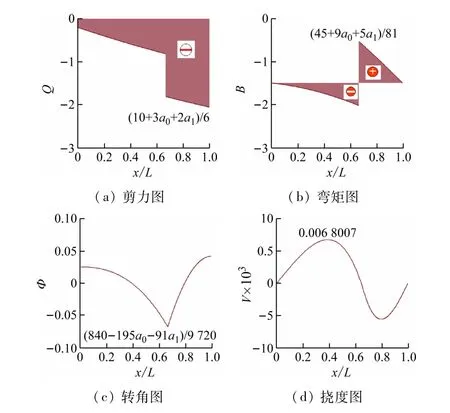
图5 n=1时简支梁的内力图和变形图

得到最大剪力、最大弯矩、最大转角及最大挠度分别为：

阶数相对误差：

2.3 将复杂分布载荷简化成抛物线分布载荷

工程中经常将复杂分布载荷简化成抛物线分布载荷，如图6 所示。在式（9）中的展开式中只取二次函数（n=2），即

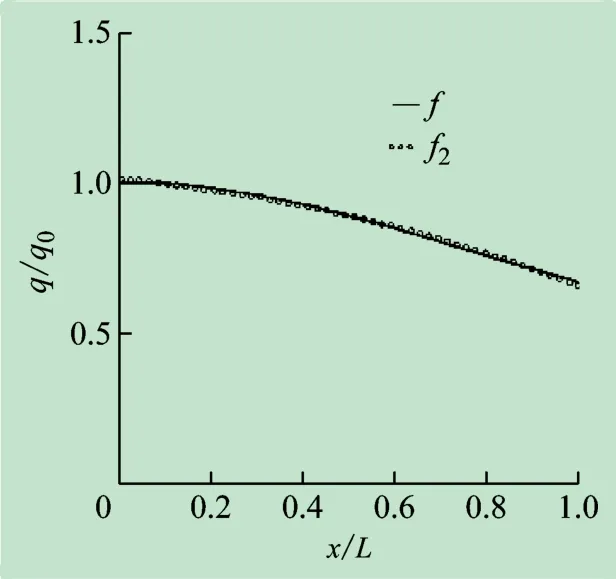
图6 抛物线分布荷载与原分布荷载

利用最小二乘法解得：a0=1.0112，a1= -0.13996，a2= -0.21727。可得分布力最大值：

用同样方法得到n=2 时，对应简支梁的内力图和变形图如图7 所示。

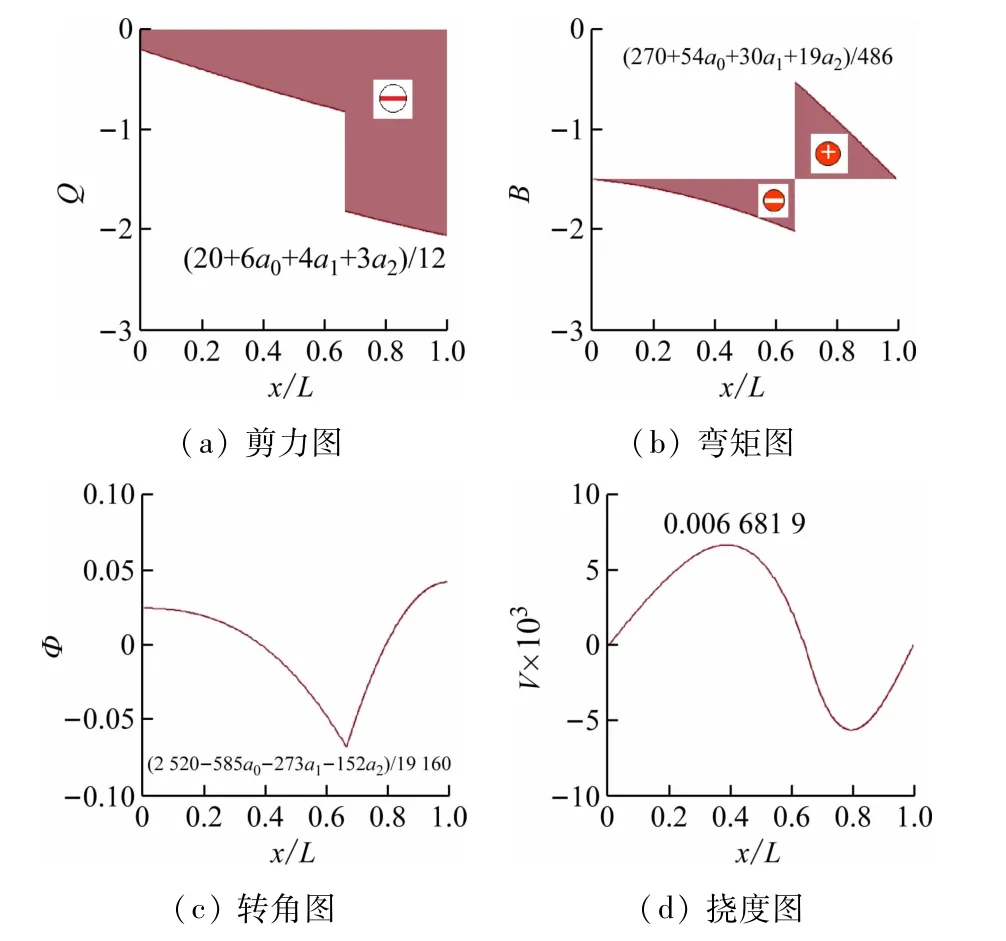
图7 n=2时简支梁的内力图和变形图

相应最大剪力、最大弯矩、最大转角及最大挠度分别为：

阶数相对误差：

2.4 将复杂分布载荷简化成三次多项式分布载荷

如图8 所示，即在式（9）中的展开式中只取3 次函数（n=3），则

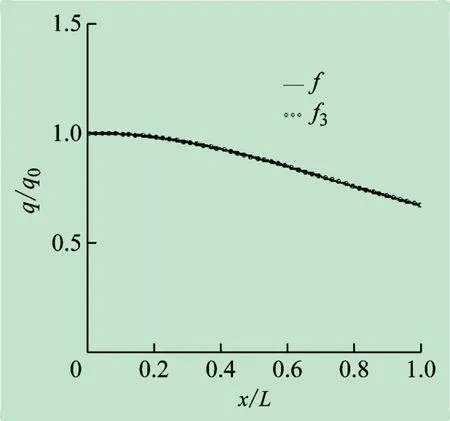
图8 三次分布荷载与原分布荷载

利用最小二乘法解得：a0=0.99919，a1=0.02417，a2= -0.63775，a3=0.28032。

用同样方法得到n=3 时，对应简支梁的内力图和变形图如图9 所示。相应最大剪力、最大弯矩、最大转角及最大挠度分别为：

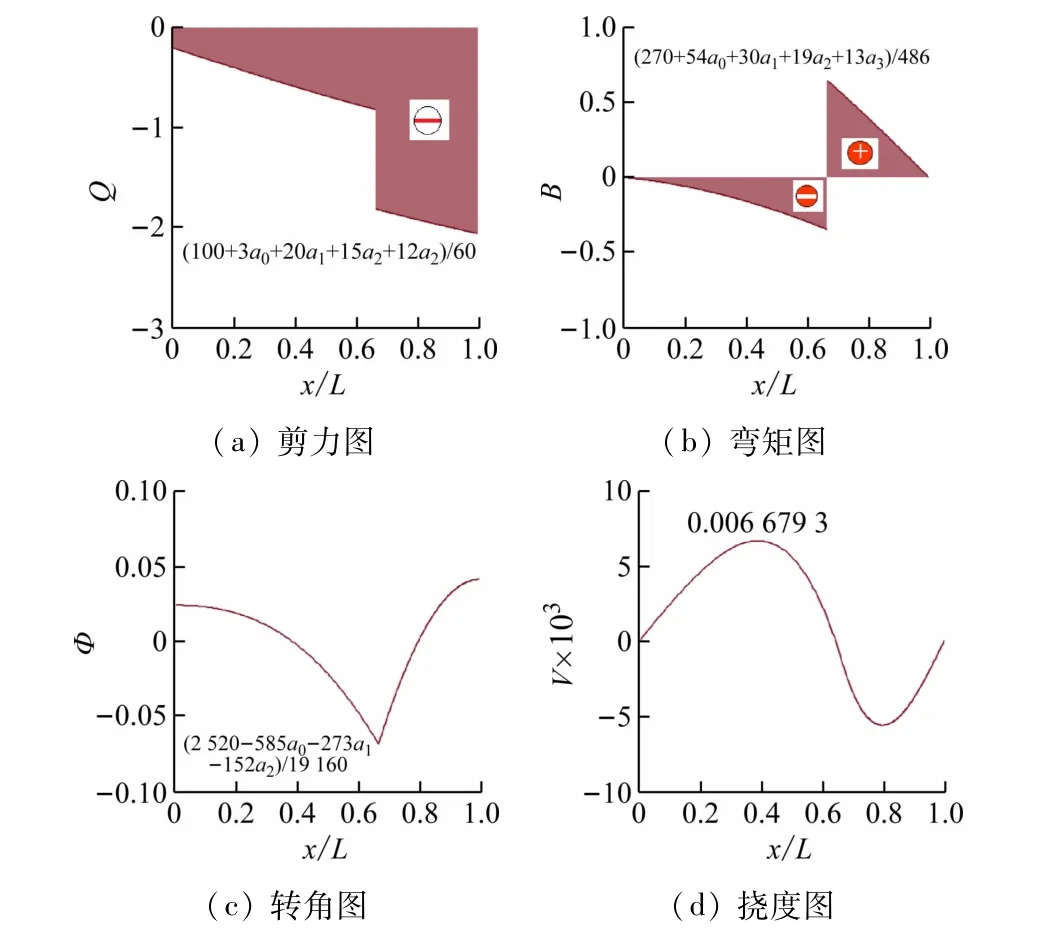
图9 n=3时简支梁的内力图和变形图

阶数相对误差：

3 结果的误差和灵敏度分析

表3 简支梁内力与变形计算结果

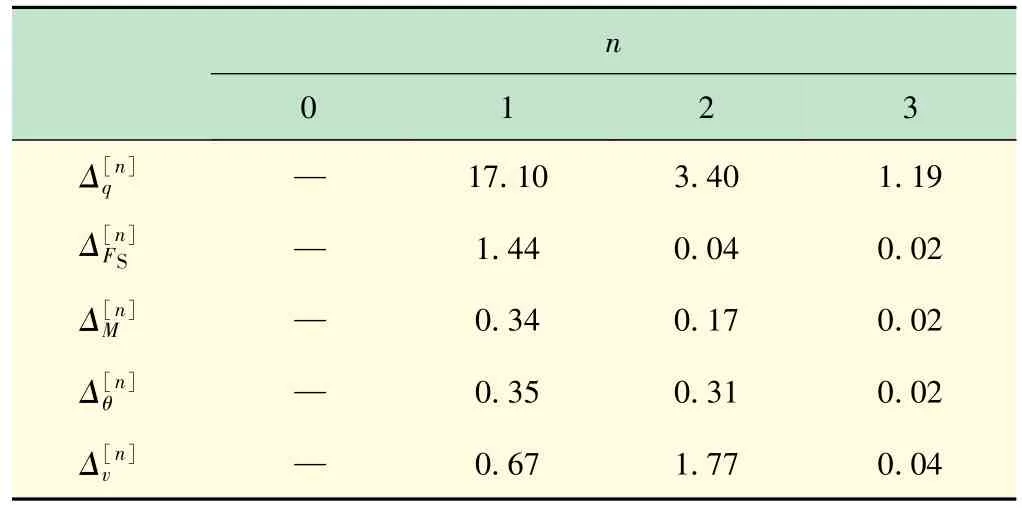
表4 简支梁内力与变形的阶数相对误差%

如果把剪力、弯矩、转角和挠度统一表示为a0，a1，a2，a3的函数

则函数的误差可表示为全微分，即

从而可得简支梁内力与变形的误差对各多项式系数灵敏度分析如表5 所示（n=3）。

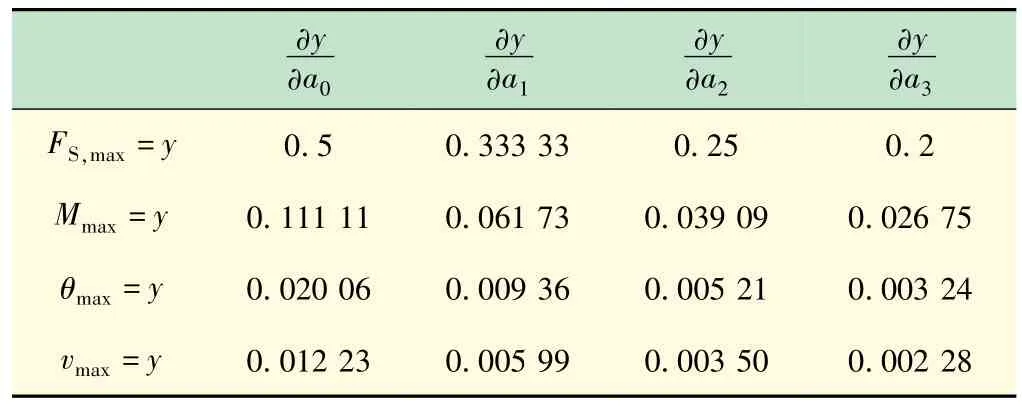
表5 简支梁内力与变形的误差对应各多项式系数灵敏度（n=3）

4 结语

本文针对复杂载荷作用下简支梁的弯曲变形问题，利用函数的泰勒级数展开法，分别选取前四项，将复杂分布载荷简化成均布载荷、线性分布载荷、抛物线分布载荷和三次多项式分布载荷。利用求解弯曲变形问题的分段独立一体化积分法，通过Maple求解程序，快速得到其解析解，并进行误差的灵敏度分析。

结果表明：按等步长将梁分成20 等分，利用最小二乘法回归成3 次多项式的分布载荷，简支梁内力与变形的计算结果满足收敛要求，阶数相对误差最小，满足工程应用。本文提出的方法与传统积分法相比，数学模型建立方法简单，求解数学模型只需要分段独立积分，采用计算机求解计算速度快，计算结果满足工程需求，可以指导桥梁等结构工程设计。