数学核心素养测评之初中数学核心素养分析

胡典顺 钟琳

胡典顺

华中师范大学数学与统计学学院教授、博士研究生导师，华中师范大学数学教育教研室主任，湖北省中学数学教学指导委员会副主任委员；《数学教育学报》《数学通讯》编委，鄂教版高中数学教材（2019年版）副主编，中国国际文化交流基金会第三届“明德教师奖”获得者；曾以访问学者的身份，由国家留学基金委公派访问美国特拉华大学；在《课程·教材·教法》《中国教育学刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇，出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识：从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著，主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。

数学核心素养测评以知识、能力、情境、核心素养“四维一体”为目标结构，其试题包含内容领域、过程领域、情境领域、核心素养领域四个测评维度。其中，核心素养领域关注学生在不同真实情境下进行数学推理并表达、应用和阐述数学，以解决问题的能力。这个过程所反映的学生在数学关键能力、思维品质以及情感、态度与价值观方面的综合表现，是本次测评的重心。本文基于“WJ市义务教育核心素养监测”项目，简述初中数学核心素养测试题所测素养的合理分布，并依据测评结果，说明初中生的核心素养表现，分析相关的影响因素及其影响程度。

一、核心素养在试题中的表现

数学核心素养的培养具有整体性、一致性，但也要考虑不同学段学生的认知发展特点。在课程标准“三会”（会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界）视角下，初中阶段的数学核心素养表现及其归类如下：抽象能力、几何直观、空间观念、创新意识倾向于“数学眼光”；推理能力、运算能力倾向于“数学思维”；模型观念、数据观念、应用意识倾向于“数学语言”。

基于数学核心素养的具体内涵，我们以数学知识为载体，设计覆盖初中阶段9个数学核心素养的测试题。为体现测评的侧重点，方便测评结果分析，每道测试题重点考查两个数学核心素养。笔者以一道测评试题为例进行说明。

案例：市场薪酬调查

市场薪酬调查是应用各种合法手段获取相关企业各岗位的薪酬水平以及相关信息，对搜集到的信息进行统计和分析，并结合企业自身的战略目标和经营绩效，确定本企业薪酬的市场定位的一种调查。黄英是某公司的市场薪酬调查员，她调查并记录了同行业的A公司中10名员工的工作年限和年薪，結果如下表所示。

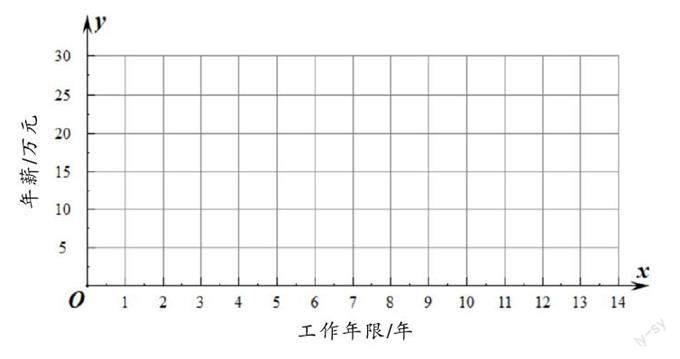
问题1  请你在下图中描出每个员工的工作年限和年薪所对应的点。其中，横坐标表示工作年限，纵坐标表示年薪。

问题2  黄英认为可以用函数“[y=1.5x+3.2]”估计A公司员工的年薪。其中，x表示工作年限，y表示年薪。请你在问题1的散点图中画出这条直线，观察图象，你认为可以用这条直线估计A公司员工的年薪与工作年限之间的关系吗？为什么？

问题3  若A公司的另一位员工年薪是13万元，他大约有多少年工作经验？

该案例立足职业情境，考查学生对“统计与概率”相关知识的应用，涉及多个核心素养。问题1需要学生通过表格数据作图，主要考查学生用图描述数据的能力，涉及几何直观与数据观念；问题2是开放性问答题，需要学生解释数据分析的结果，主要考查抽象能力和模型观念；问题3考查学生根据数据分析结果作出判断和预测的能力，主要聚焦数据观念和运算能力。

设计测评卷时，我们需要合理设计各个核心素养的考查比重，以保证准确、全面地考查学生的数学核心素养水平。经过对课标、教材等的分析，命题人将初中核心素养测评卷中各个核心素养的分数占比规划如下：“数学眼光”“数学思维”与“数学语言”三部分核心素养的分数占比分别为28%、37%、35%。其中，运算能力考查占比最大，为23%；其次为应用意识与推理能力，分别为16%、13%；空间观念考查占比较小，为2%；其余各素养考查占比分布均匀。

二、测评结果及分析

1.数学核心素养测评结果

试题的得分情况是数学核心素养测评结果的直接表现。为了解学生在素养测评中的表现，笔者基于4025份有效数据，借助SPSS26.0进行描述统计，得到学生得分最大值为100分（满分）、最小值为1分、均值为51.61分，说明学生成绩较好；分数的标准差为22.53，说明学生的核心素养水平差异较大。

从“三会”视角出发，学生在各个核心素养上的得分均值、得分率（均分占总分的比例）等分布情况，如表1所示。

由表1可知，参评学生在“数学思维”方面表现最好，在“数学眼光”方面表现良好，在“数学语言”方面表现欠佳。其中，几何直观的得分率最高，为66.4%；数据观念、运算能力、推理能力与模型观念的得分率均在50%以上；而空间观念的得分率较低，仅为33.4%。这表明学生的空间观念有待提升，教师要在教学中强化学生空间想象力的培养，使学生更好地理解现实生活中空间物体的形态与结构。

2.数学核心素养水平分析

为精确了解学生核心素养的发展水平，本测评采用PISA测试使用的精熟度水平划分方法作为评价标准（如表2所示），根据学生在不同水平上答对的概率，刻画学生的水平等级，从而更好地对学生的分数作出解释。

由表2可知，总体上，学生数学核心素养精熟度水平分布均匀，4级、5级、6级的比例较高。其中，占比最高的是4级水平，为19.5%。从“三会”视角来看，“数学眼光”“数学思维”及“数学语言”中占比最高的均为6级水平，分别占比20.0%、19.0%、19.9%，占比最低的均为0级水平，其余各级精熟度水平占比接近。这说明学生在“数学眼光”“数学思维”及“数学语言”三方面都具有较高水平。

观察“累计占比”，我们可以发现：总体上有14.3%的学生精熟度水平在6级以上，能对复杂问题情境进行建模，思维水平较高；约有33%的学生精熟度水平在5级以上，能通过比较、评估，选择适当的问题解决策略，进而解决相关的复杂问题；有超过50%的学生精熟度水平在4级以上，能在复杂情境下准确运用模型，能联系实际选择与整合包括符号性表征在内的不同表征方式，能进行灵活地推理；约有70%的学生精熟度水平在3级以上；超过84%的学生精熟度水平在2级以上。也就是说，大部分学生都具备2级以上的精熟度水平，能够进行简单的直接推理。

为直观呈现学生成绩在各个素养上的精熟度水平分布，笔者绘制了如下百分比条形图。

由上圖可知，应用能力、数据观念、推理能力、几何直观与运算能力的各级精熟度水平分布比较均匀；模型观念的0级精熟度水平占比最低，仅为1.2%，而6级精熟度水平占比达37.9%；创新意识、空间观念与抽象能力的0级精熟度水平占比较高，均超过20%。其中，空间观念的精熟度水平分布极端，0级精熟度水平占比为66.1%，6级精熟度水平占比为32.0%。这说明学生的空间观念素养差异较大，教师应该适当调整教学策略，强化学生的空间观念。

3.数学核心素养回归分析

数学核心素养表现不仅是日常教学的结果，也与学习环境、外界因素、学生对学习的认识等息息相关。关注学生的数学学习基本情况、数学学习价值观与数学学习品格，可以帮助我们更好地了解影响学生数学核心素养表现的因素。笔者结合本测评调查问卷的数据，利用多重线性回归分析法做具体分析。

多重线性回归分析的目的是建立一个筛选自变量的最优回归模型，将没有影响的自变量和共线性强的自变量剔除，将对因变量有意义的自变量纳入模型。SPSS26.0中，自变量筛选的准则为统计量显著性检验准则，即通过对偏回归系数进行显著性检验，选择有统计学意义的自变量，进而构成回归模型。

以“学生数学学习情况、数学思维品质、数学学习态度对测评卷总分的影响”分析为例，笔者用SPSS26.0进行如下操作：选择【分析】g【回归】g【线性】；将“总分”选入【因变量】列表框，将“数学学习情况”“数学思维品质”“数学学习态度”选入【自变量】列表框，在【方法】选项中选择【步进】；在【统计量】选项卡中勾选“共线性诊断”；最后点击【确定】。

上述操作中，我们在【方法】选项中选用“步进法”，即事先设定自变量进入、剔除的标准，每次向模型中引入一个新变量，就对原来模型中的自变量是否还有统计学意义进行一次检查，直至既没有自变量能够进入方程，也没有自变量从方程中剔除。经由此操作，我们得到自变量筛选结果，如表3所示。

由表3可知，通过逐步分析，共建立过3个回归模型，最终建立的模型为模型3，引入“数学学习情况”“数学思维品质”“数学学习态度”3个自变量。[R2]为决定系数，用于衡量线性回归模型的拟合度。[R2]值为0.236，说明自变量能解释23.6%的因变量变异。

为衡量回归模型3是否有意义，笔者进行显著性检验，结果如表4所示。表中[F]值为414.691，[p]值小于0.05，说明建立的回归模型具有统计学意义。

笔者进一步分析模型3中各因素回归系数，结果如表5所示。

由表5可知，共线性检验中各自变量的容差均大于0.1且方差膨胀因子VIF小于5，说明自变量满足多重线性回归的独立性条件；非标准化系数中各自变量的系数[B]均大于0，说明“数学学习情况”“数学思维品质”与“数学学习态度”对学生测评总成绩均有正向影响。如“数学学习情况”包括学生的数学成绩、数学学习状态、目前学习有无困难、对数学学习的期望和信心等要素，“数学学习情况”系数最大，表明：学生的数学学习成绩越好，学习状态越佳，对数学学习的期望和信心越高，学生的测评成绩就越好。

回归分析是线性因果关系研究的基础，可以在一定程度上反映自变量与因变量的关系，但只能分析变量之间的直接效应，无法处理不可测量的变量（潜在变量），无法分析间接效应，不能很好地反映复杂的因果关系模型。后续，我们可以考虑采用结构方程模型进一步探析影响学生核心素养表现的因素。

（钟琳系华中师范大学数学与统计学学院硕士研究生）

责任编辑  刘佳