让几何画板用在当用时

刘小宝 徐利萍 汪屹

“几何画板”软件的“实时数据”“动态演示”等功能在揭示概念本质、扩大验证样本、演示图形变化过程等方面具有优势。笔者依托《平行四边形的认识》的教学进行了“几何画板”的应用研究，旨在帮助学生突破学习难点，实现深度学习。

一、动态呈现图形生成过程，揭示概念本质

两组对边分别平行的四边形叫作平行四边形。显然，平行四边形是从边的特殊位置关系定义的。然而，在常规教学条件下，对于平行四边形“对边平行”这一显著特征，学生不仅感受不深刻，还会遇到验证困难的问题。一般地，验证平行四边形对边平行需要借助中学几何中的平行判定定理，小学生没有这个认知基础。此种情况下，几何画板的“动态演示”和“实时数据”功能可以发挥辅助学习作用。

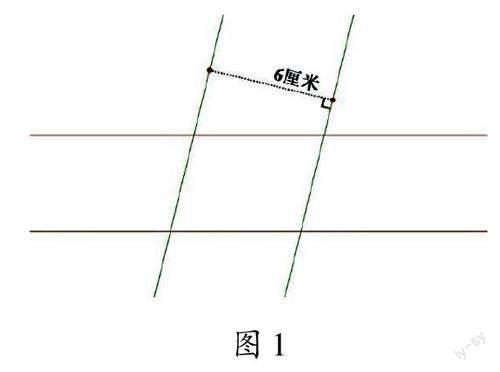
课堂上，在初次呈现平行四边形时，教师不是直接给出图形，而是先用几何画板动态生成两组相交的平行线，让学生找出平行四边形，再通过动态演示，让学生见证平行四边形“生成”的过程，初步感知平行四边形。随后，教师用几何画板动态演示平移一组平行线之间的垂线段的过程，并实时顯示这条垂线段的长度（如图1）。学生观察到长度不变，验证了平行四边形两条对边所在直线不相交，进而得出平行四边形对边平行的结论。

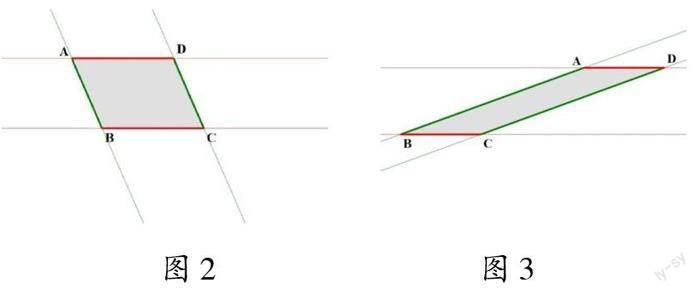
在揭示平行四边形概念时，教师用几何画板拖曳图形，让平行四边形不断改变形态（如图2、图3所示），并提问：这些图形还是平行四边形吗？为什么？在教师的启发下，学生发现这些图形的共性是对边始终保持平行。随后，教师引导学生归纳平行四边形的概念：什么样的图形是平行四边形呢？学生很容易得出：两组对边分别平行的四边形叫作平行四边形。

直观的演示、动态的呈现使学生观察到平行四边形两组对边分别平行的关系，深刻地理解了概念的本质。

二、扩大验证特征的样本量，增强结论可信度

平行四边形除了对边平行这个显著特征，还有对边相等、对角相等的特征。学生一般通过猜想和动手操作，验证并理解平行四边形对边相等、对角相等的特征，但是由于测量有误差、样本数量有限等，所得结论的可信度不足。几何画板随意变换平行四边形的形态并实时生成相关数据的功能，能扩大验证所需的样本数量，准确显示相关数据，增强结论的可信度。

首先，学生在教师引导下通过测量手中的平行四边形卡片，猜想其对边相等、对角相等。接着，教师以“是不是任意一个平行四边形都有这样的特征呢”，引导学生提出扩大样本数量，进一步验证的需求。然后，学生用几何画板拖曳图形，将平行四边形随机变形。几何画板自动同步显示平行四边形的边长数据和角的度数。在样本增多、形态随机，甚至出现极端情况的前提下，学生通过观察数据，充分感受到任意一个平行四边形都具有对边相等、对角相等的特征。

以上教学，教师引导学生在变化中找不变，轻松地达到了认识平行四边形特征的目标。

三、演示图形转化的过程，培养几何直观

长方形、正方形都是特殊的平行四边形。对于这三种图形的关系，随着几何画板中的图形多次在一般平行四边形和长方形之间转换，学生已经有感性认知，教师可帮助学生深化认知，培养几何直观。

首先，教师用几何画板将一般的平行四边形拖曳成长方形，并引导学生关注角度数据的变化。当四个角呈90°时，学生马上辨认出长方形。教师提问：长方形是平行四边形吗？为什么？学生抓住动态演示过程中两组对边始终分别平行这一概念本质，肯定地回答“是”，直观地认识到长方形是特殊的平行四边形。教师追问它特殊在哪里，学生通过观察角度数据的变化，很容易得到“角特殊”这一结论。教师进一步引导：能不能让它变得更特殊一点，变成正方形？学生在教师的启发下关注边的特殊性，并在几何画板实时显示边长数据的情况下进行图形拖曳的操作。动态演示的过程让学生充分体会到正方形角特殊，边也特殊，它也是特殊的平行四边形。

几何画板将静态的图形进行动态转换，使学生不仅理解了长方形和正方形具备平行四边形的特征，还深刻地认识到它们各自的特殊之处。这样教学既巩固了学生对平行四边形概念本质的理解，又拓展了概念的外延。

四、直面学生的困惑点，发展空间观念

认识平行四边形的高是学生学习的难点。学生很容易找到水平方向的底所对应的高，但是向其他方向作高时经常出现找错对边的情况。另外，对于平行四边形外的高，学生很难想象并理解。教师可以利用几何画板给学生的空间想象以具象支撑，帮助学生突破难点。

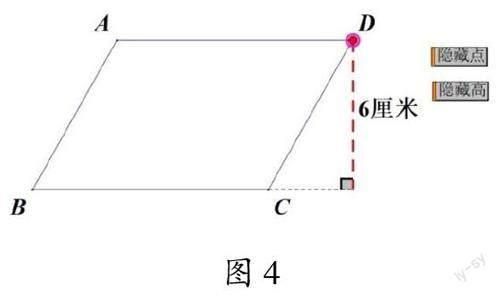
学生自学微课“平行四边形的高”后，教师从平行四边形一条边中间的一点引出一条垂线段，并提问“从这点出发画的这条垂线段是高吗”，引导学生聚焦“找准点”，进一步理解“边上一点”指的是边上的任意一点。然后，教师引导学生思考“高”的本质：上下这组对边之间有多少条高，长度相等吗？学生发现：“高”实际上是平行四边形对边之间的垂线段。同时，教师在几何画板中动态拖拽高的位置，实时显示高的长度数据，让学生直观地看到高在图形外的情况（如图4），唤醒学生对平行线之间的距离处处相等的已有认知，使他们轻松理解一组对边之间有无数条高且长度相等。

随后，教师先演示从平行四边形“斜边”上的一点引出垂线段（如图5），并提问“这条线段是这个平行四边形的高吗”，引导学生聚焦“找对边”，然后通过追问“对边是哪条边”，让学生明确应该找点所在边的对边，体会找对边的重要性。

本节课的教学中，几何画板在学生的问题形成处、思维发展处、能力提升处充分发挥辅助学习作用。教师在图形教学中应用几何画板让理有形的依托、形有数的支撑，有利于发展学生的空间观念，提升学生的数学素养。

（作者单位：刘小宝，武汉市教育科学研究院；徐利萍，武汉市武昌区教师培训中心；汪屹，武汉市武昌区中山路小学）

责任编辑  刘佳