基于元学习的压制式干扰识别方法研究

张 然, 刘 悦, 潘成胜

(大连大学,a.信息工程学院; b.通信与网络重点实验室,辽宁 大连 116000)

0 引言

在无线通信系统中,随着电磁环境的日益复杂,需要对环境中的各种干扰进行检测和识别,为通信接收机生成有效的抗干扰决策提供依据。例如,在卫星通信和移动通信等领域,通信设备可以通过先提前检测和识别干扰信号,再采取相应的干扰消除技术,提高通信质量和频谱效率。因此,干扰识别技术逐渐成为无线通信系统的研究热点。

目前,常用的信号识别方法有阈值比较法和基于神经网络的识别方法。传统的阈值比较法[1-3]是通过专家经验来提取信号的特征参数进行识别的,会产生特征提取不全和依赖性的问题,所以目前更多地会采用具有自组织性和自适应性的神经网络进行信号识别的方法[4-9]。但是神经网络的训练需要大量的数据作为支撑,而干扰信号的获取十分困难,且干扰信号数据集进行标注的成本也比较高,所以,在干扰信号数据量小的情况下,存在识别率不高的问题。针对这个问题,有研究提出了基于神经网络的小样本干扰信号识别方法。文献[10]提出用增强深度卷积生成对抗网络来实现雷达信号小样本数据增强的方法,其本质是通过对抗网络产生逼近现实的信号样本来扩充小样本的数量使识别率提高,并不是直接采用小样本的数据;文献[11]针对雷达小样本目标识别问题,根据所拍摄的目标图片,结合残差网络和基于欧氏距离的度量学习提出了识别方案,然而,残差网络提取出的是多维特征向量,基于欧氏距离的度量学习没有考虑同种类多维向量之间的相关性,所以分类识别的准确度受限。

为了进一步提高压制式干扰的识别率,提出了一种Holder系数与神经网络相结合的算法,使用Holder系数来度量频率响应的变化。由于同种类型干扰信号的Holder系数十分接近,且具有较好的聚类效果,所以文献[12]提出将提取的Holder系数与K-means算法相结合进行信号识别的方法。但是K-means算法对初值敏感,不同的初值可能会使聚类结果不稳定。相比较之下,神经网络受初值影响小,且有比较稳定的聚类结果,因此对比与K-means算法相结合的识别方法,Holder系数与神经网络相结合的方法在理论上更可以提升识别准确率。

本文以压制式干扰为研究对象,为了提高小样本干扰信号的识别精度,在元学习中,首先将干扰信号的时频图输入残差网络得到的特征向量与Holder系数相结合,其次将时频图输出的特征向量分为编码向量和一个协方差矩阵,求出干扰预测值并计算欧氏距离来实现对小样本的干扰分类,以提高干扰信号的识别率。

1 压制式干扰信号模型

1.1 压制式干扰的种类

对于压制式干扰的识别[7],主要包括瞄准式窄带干扰(Aiming Narrow Band Jamming,ANBJ),部分频带噪声干扰(Partial Band Noise Jamming,PBNJ),随机梳状谱干扰(Random Comb Jamming,RCJ),周期脉冲噪声干扰(Periodic Pulse Noise Jamming,PPNJ)和调频类干扰(Frequency Modulation Jamming,FMJ)。

瞄准式窄带干扰包括:模拟调制类的幅度调制(Amplitude Modulation,AM)和噪声幅度调制(Noise Amplitude Modulation,NAM)干扰,数字调制类的二进制相移键控(Binary Phase Shift Keying,BPSK)、二进制频移键控(Binary Frequency Shift Keying,BFSK)和正交相移键控(Quaternary Phase Shift Keying,QPSK)干扰,连续波(Continuous Wave,CW)干扰,窄带噪声干扰(Narrow Band Noise Jamming,NBNJ)等。

随机梳状谱干扰包括:梳妆谱噪声干扰(Comb Spectrum Noise Jamming,CSNJ)和多音干扰(Multi-Tone Jamming,MTJ)。

调频类干扰包括:噪声调频(Noise Frequency Modulation,NFM),线性调频(Linear Frequency Modulation,LFM)和正弦调频(Sinusoid Frequency Modulation,SFM)干扰。

接收信号r(n)的采样信号为

r(n)=s(n)+j(n)+w(n)n=1,2,…,N

(1)

式中:s(n)为接收到的通信信号;j(n)为干扰信号;w(n)为高斯白噪声;N为采样长度。

1.2 压制式干扰的时频图像

为了进行干扰信号特征的计算,首先需生成干扰信号时频图,用于后续输入到神经网络中。本文研究选择短时傅里叶变换(Short-Time Fourier Transform,STFT)的方法对干扰信号进行时频分析,其中,频谱图SPx(t,f)可表示为

(2)

式中:t和f分别表示时间和频率的离散参数;w(t-τ)为窗函数。

对干扰信号进行时频分析,将其转换成可以输入到残差神经网络处理的224×224(单位为像素)的时频图片,以便输出干扰信号时频图的编码向量和其对应的协方差矩阵,为下一步求干扰信号预测值奠定基础。

压制式干扰信号时频图如图1所示。图中,压制式干扰信号的干噪比(Jamming-to-Noise Ratio,JNR)设置为20 dB。

图1 干扰信号的时频图

2 基于元学习的干扰识别算法

为了解决小样本干扰信号的识别问题,提出一种基于元学习的压制式干扰识别方法。干扰识别网络整体结构如图2所示。

图2 干扰识别网络结构

首先,对各类干扰信号的Holder系数进行提取,并将该干扰信号生成的时频图输入到残差网络中;然后,将残差网络输出的干扰信号特征向量与提取的Holder系数在全连接层中进行拼接,再对网络模型进行训练;同时,根据添加高斯协方差矩阵的欧氏距离度量算法,计算出每类支撑集的原型;最后,输入干扰信号的测试集分别计算与每类原型的距离,与支撑集原型距离最小的类别即为测试集所属的信号类别,完成信号的识别。

2.1 Holder系数的提取

Holder系数用来描述两个不同信号之间的相似性[13],设有两个离散正值信号序列{s1(i)≥0,i=1,2,…,N}和{s2(j)≥0,j=1,2,…,N},N为离散点数。则数学模型可定义为

(3)

式中:H为Holder系数,0≤H≤1;参数p>1,q>1,且1/p+1/q=1。

在计算Holder系数之前,先对信号做傅里叶变换得到频谱,再对频谱进行能量归一化。归一化的目的是使特征具有相同的度量尺度。采用最大-最小归一化方法,可表示为

(4)

式中:x*为归一化后的干扰信号频谱;x为干扰信号频谱;xmin和xmax分别为干扰信号频谱的最小值及最大值。归一化后,干扰信号数据各维度参数的值均在[0,1]之间。

为了计算Holder系数,同时引入两个第三方信号序列——矩形信号频率序列和三角信号频率序列,作为参考信号序列[13]。矩形信号频率序列能量分布较为均匀,三角形信号频率序列较为集中,因而比较适合作为参考信号序列。

矩形信号频率序列为

(5)

三角信号频率序列为

(6)

其中:N为信号的频率点数;k为频率序列的索引。

则信号频率序列{s(i)}对应的Holder系数特征包括两个系数值H1和H2,可分别表示为

(7)

(8)

最终,每个干扰信号分别与三角序列和矩形序列计算出Holder系数H=[H1,H2],用于提高干扰信号的聚类效果。

2.2 多维特征向量的计算

小样本的学习方法通常采用特征结构为4层的卷积神经网络[14-15],该网络易于训练,但学习能力有限。而残差网络中的卷积特征学习具有良好的泛化能力和非常低的敏感度,可用来提高实际系统的信号检测和分类的性能[16-20],从而提高信号识别的准确率。

在残差网络的前向传播过程中,可以通过跃过一层或者多层连接的方式得到恒等映射。恒等映射的主要作用是在增加层数后,若模型层数大于或等于浅层数,依旧能保持模型的性能[15]。

残差网络结构设计如图3所示。本文构建了一个10层残差网络结构,该结构包含一个7×7的卷积层,一个3×3的最大池化层,两个卷积层为3×3、通道数为64、步长为2的残差块,以及两个卷积层为3×3、通道数为128、步长为2的残差块。

图3 残差网络结构

在残差网络中,设全连接层输出的特征向量为X=[X1,X2,X3,X4,…,X127,X128]。将提取到的Holder系数与该特征向量进行拼接,得到的新特征向量为X=[X1,X2,X3,X4,…,X127,X128,H1,H2],将其作为残差网络新的全连接层。在此基础上,通过将干扰信号支撑集输入修改后的残差网络进行模型训练,得到残差网络的权重,再将干扰信号测试集的时频图输入带有权重的残差网络,输出识别结果。

2.3 基于元学习的干扰识别

基于度量的元学习方法是以任务之间的相似性为基础,找到过去训练过的相似任务,并借鉴经验,以加速新任务的完成。度量函数可以最小化相似任务之间的距离,最大化不同任务之间的距离,提高任务处理的效率。

传统的度量学习[11]是基于欧氏距离度量的原型网络。本文考虑到多维特征向量之间的相关性,通过给欧氏距离添加高斯协方差矩阵来度量信号之间的相似性。即除了嵌入生成的数据点之外,还在数据点周围添加了一个置信区域,该区域以高斯协方差矩阵为特征。置信区域有助于描述单个数据点的质量,在有噪声且同质性低的情况下十分有效。另外,对于每个不同的类,传统的欧氏距离都定义的是一个半径相等的范围,而添加的高斯协方差矩阵能更好地从不同的维度学习出一组更好的度量距离[21-22],使分类的结果更加准确。不同欧氏距离的分类结果如图4所示。

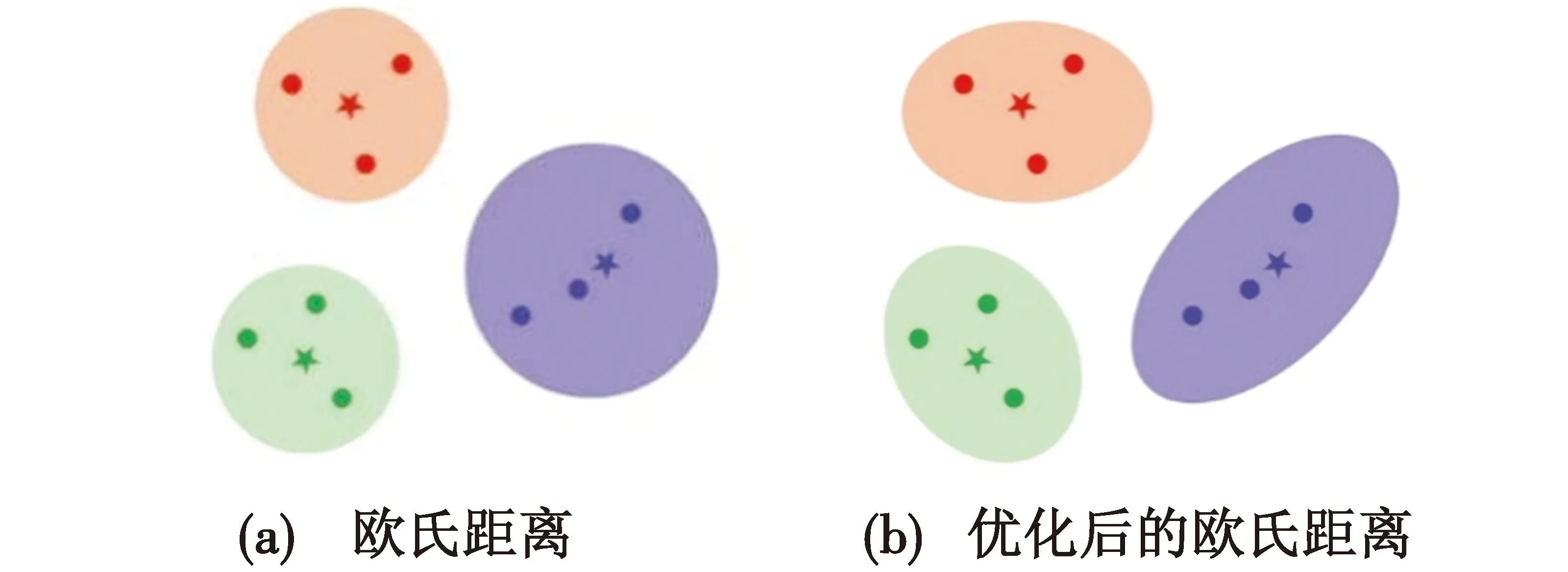
图4 不同欧氏距离的分类结果

改进后的基于度量的元学习干扰识别算法如下。

1) 设干扰信号时频图的数据集为x,类标签为y,数据集D={(x1,y1),(x2,y2),…, (xi,yi)}。从数据集D的各类别中不放回地随机抽样数据点,以组成支撑集。

2) 同样,随机抽样干扰信号数据集组成查询集Q。

3) 将各类别干扰信号的支撑集传入残差网络,输出编码向量和其相关的协方差矩阵Sraw。协方差矩阵Sraw采用维数是1的半径分量,为每一个支撑集的图像生成一个置信区间的表征。最后干扰信号各类别的置信区间所构造的协方差矩阵可以表示为Σ,即

Σ=diag (σ1,σ2,σ3,σ4,σ5,… )

(9)

式中:Σ为常数对角矩阵;σi为通过原始的输出Sraw得到的第i个结果。

4) 计算协方差矩阵Sraw的逆矩阵S

S=1+softplus(Sraw)

(10)

式中,softplus(x)=lb(1+ex),保证了S>1。

5) 计算干扰信号支撑集中每个类的原型pc,则

(11)

6) 在完成干扰信号支撑集中每个类的原型计算后,输入干扰信号时频图查询集进入残差网络后输出向量xi。

7) 计算干扰信号查询集向量xi与类原型pc之间的距离Dis为

(12)

8) 计算干扰信号原型与查询集向量的距离后,预测查询集y的类,它与干扰信号原型的距离最小,即

y=arg minc(Dis)。

(13)

查询集依次与每个类的原型比较距离,当y最小时,此查询集就属于该原型的类别,即识别出干扰信号的所属类别。

3 实验结果与分析

本文干扰信号的仿真环境为加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道。为了验证所提方案的可行性,对干扰信号识别的准确率进行了比较和验证。仿真中使用的技术框架是Keras,实验所使用的电脑CPU为6颗E5-2680 v4,GPU为RTX 2080 Ti。

3.1 仿真参数设置

对于每一类干扰信号,选用协方差矩阵的半径分量作为置信区域,压制式干扰支撑集分别设置为1个样本和5个样本,测试集为100个样本,进行训练与识别。利用软件生成干扰信号的Holder系数和时频图,并将Holder系数以及时频图的路径存储于同一个txt文件中,以实现系数与图的一一对应。

仿真实验中,基于实验平台的参数配置,设置干扰的带宽为50 MHz,采样率为61.44 MHz,干扰持续时长为20 μs,采样点数为12 288。干扰信号的仿真参数设置如表1所示。

3.2 干扰信号识别率验证与分析

3.2.1 神经网络与K-means识别效果对比与分析

对于每一类干扰信号,JNR取值-30～10 dB,每间隔5 dB取一次值,每种干扰样式的每个JNR产生500个干扰信号。其中,每个JNR下400个干扰信号作为训练集,100个干扰信号作为测试集,进行训练与识别。

为了验证Holder系数与神经网络结合比与K-means聚类方法结合识别率更高,对神经网络方法与K-means方法进行识别效果对比,并对每个JNR下信号识别的准确率取平均值,结果如图5所示。

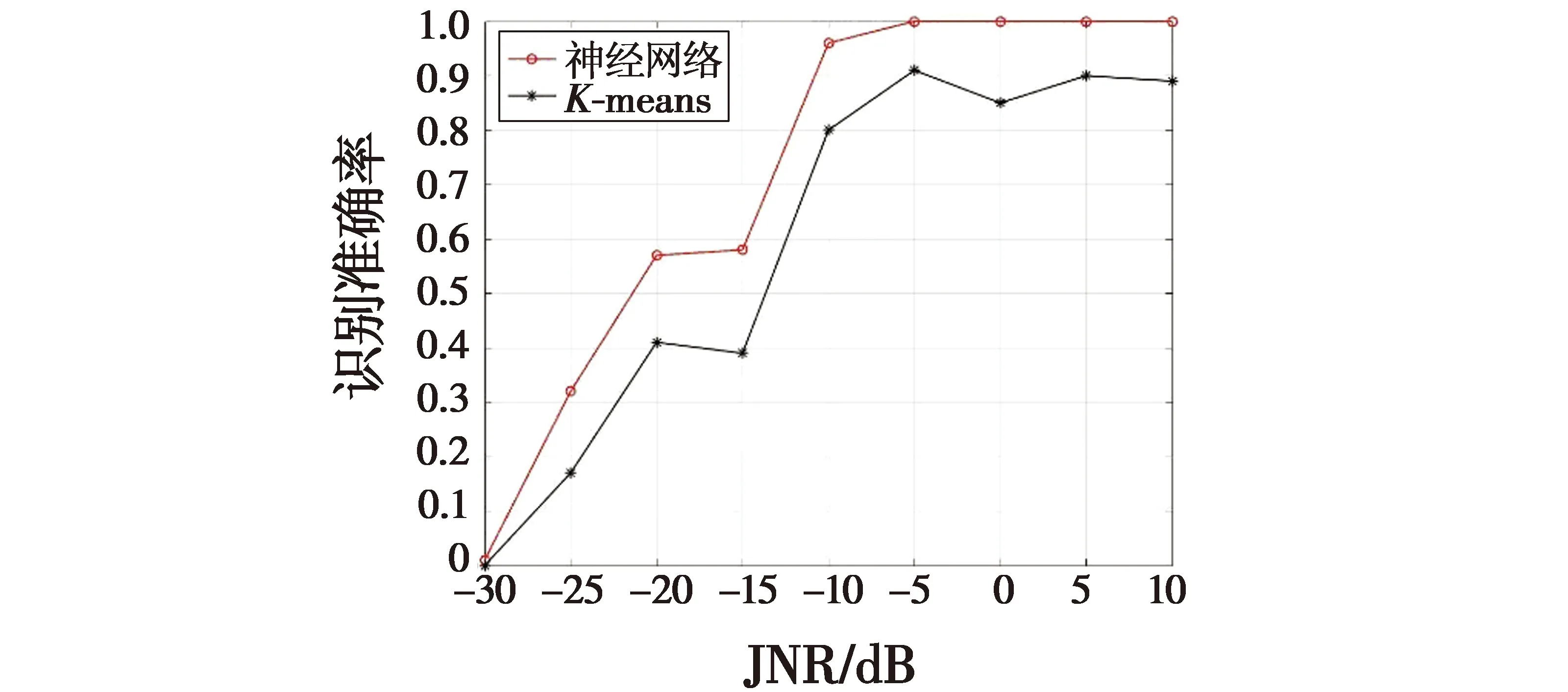
图5 神经网络与K-means识别效果对比

由图5可知,JNR的值高于-5 dB以后,神经网络对干扰信号识别率已经可以达到100%的准确率,而K-means算法对干扰信号的识别率仍然在90%左右,这是由于算法聚类的结果不稳定,导致了识别率的波动。由此可以得出,采用神经网络比K-means算法的识别率高。

3.2.2 小样本信号识别率验证与分析

本文提出利用元学习在小样本标记的数据下进行时频图的特征提取,即使面对未训练过的对象也不需要构建新的模型,能够有效提高模型的泛化能力。为了验证本文算法在小样本干扰信号识别方面的有效性,将其与传统基于欧氏距离的元学习方法进行对比。

在仿真中,利用实验平台配置的预训练数据集中大量带有标签的数据,估计出具有普适性、能推广到ANBJ的规律,加速模型在ANBJ小样本数据集上准确推理的过程,提高模型的泛化能力,以达到快速识别小样本干扰信号的目的。

仿真参数设置结合实际情况,讨论JNR分别为-10 dB,0 dB和20 dB时的干扰信号识别。选用协方差矩阵的半径分量作为置信区域,以ANBJ中的7类干扰为例,设置测试集为100个样本,干扰支撑集样本数分别为1和5。具体的验证手段如下:

1) 将实验平台提供的信号数据集输入到残差网络中进行训练,得到预训练权重,并迁移到小样本干扰信号训练的残差网络中作为初始权重;

2) 依次将ANBJ中的干扰类别输入到带有预训练权重的残差网络中,并不断将上一个类别训练出的权重参数提供给下一个类别作为初始权重;

3) 将ANBJ分别为1个样本和5个样本的干扰信号时频图作为支撑集输入到残差网络中,将输出的特征向量分为嵌入向量和置信度后,计算出ANBJ中每一类的原型,计算过程见2.3节;

4) 将ANBJ中每个测试集的100张时频图输入到残差网络中,分别用基本欧氏距离和优化后的欧氏距离计算测试集到每个种类原型的距离,距离最小的种类为所属的干扰信号类别,并记录不同方法下小样本识别的准确率。小样本识别准确率对比仿真结果如表2所示。

表2 小样本识别准确率对比

由表2可知,在不同的JNR下,本文算法的识别率均高于传统算法。另外,本文算法相比传统算法识别准确率的提升率随着干扰信号强度的增大而增加,在支撑集只有1个样本的情况下,提升率从0.8个百分点上升到了3个百分点;在支撑集有5个样本的情况下,提升率从1.1个百分点上升到了9.5个百分点,进一步证明了本文算法对干扰信号识别的有效性。

4 结束语

针对小样本干扰信号识别率低的问题,本文提出了基于Holder系数和残差网络的信号特征提取方案以及基于改进度量的元学习方法。对干扰信号仿真数据集进行学习,仿真实验结果表明,优化后的干扰识别算法在小样本数据集1-shot与5-shot的任务中,提升率分别增加了约2.2个百分点和8.4个百分点,证明了所提出的基于元学习的干扰识别算法的有效性和优越性。在实际应用中,当面对未知干扰且干扰信号样本量较少时,本文算法可以对干扰特征进行快速学习,有效提升识别效率,为后续抗干扰决策提供有力依据。在未来的研究中,将进一步研究瞄准式窄带干扰特征的提取,加大提取特征的差异性,得到更为优越的干扰信号识别结果。