空地协同作业场景下无人机快速路径规划与自主降落技术

曹宇辉, 解明扬, 李嘉铭, 张 民, 王从庆

(南京航空航天大学自动化学院,南京 211000)

0 引言

空地协同作战作为未来战争的重要作战方式之一,对无人机(UAV)与无人车(UGV)的协同性、自主性和智能化提出更高的要求。无人车具有强大的负载和出色的续航能力,而四旋翼无人机相比无人车具有更广阔视野、更高机动性和灵活性,通过两者优势互补,实现空地协同作战任务、倍增作战效能。空地协同作战任务场景中,无人机路径规划与自主降落技术是任务感知、侦察、保障支援和回收的关键。其中路径规划部分,向无人机给定任务目标后,要求无人机能够动态感知周围环境,并根据感知范围内有限环境信息实时进行航迹规划的同时,躲避地面雷达探测等危险区域;在自主降落过程中,要求无人机能够快速、准确地降落到无人车平台,这是无人机能量补给和回收的关键。

目前,国内外学者针对无人机路径规划和空地协同降落问题分别进行了研究。其中,无人机路径规划主要分为全局路径规划和局部路径规划技术[1]。全局路径规划是在环境信息完全已知情况下寻找路径,主要包括A*算法[2]、可视图法[3]、模拟退火法[4]、遗传算法[5]和粒子群算法[6]等,全局路径规划算法一般能够找到最短路径,但是计算时间更长,同时需要提前获取全局地图信息,无法实现动态环境下路径规划;局部路径规划算法是在未知或部分已知环境下,找到从起点到终点的可行路径,主要包括人工势场法[7]、VFH算法[8]、神经网络算法[9]、动态窗口法[10]和强化学习法[11]等,这类算法复杂度低、计算时间快,不依赖全局环境信息就可以完成路径规划,但是很难找到最优路径且容易陷入死区。在空地协同降落方面,文献[12]设计了一种新型嵌套三角形图案作为无人机自主着陆地标,进一步提出了一种快速轮廓角点检测算法,有效减少了识别过程中的计算量、降低了复杂度;文献[13]提出了GPS丢失场景下基于单目视觉的无人机新型姿态控制方法,在小波分析中引入自适应卡尔曼滤波器成功滤除了高频噪声;文献[14]提出了二维码位置与姿态估计算法及其识别方法,采用平行线消失点与Levenberg-Marguardt(L-M)优化算法相结合的方法实现四角点检测,检测精度达到厘米级,但算法实时性较差。

综上所述,目前多数学者将无人机路径规划与空地协同降落问题单独进行研究,而在实际空地协同作战场景中,要求无人机能够一体化实现快速路径规划与自主精准降落,这对搭载有限计算资源情况下无人机路径规划以及自主降落算法的实时性与精确性提出了更高要求。目前改进的A*算法往往受限于无人机机载计算机算力。此外,无人机路径规划与自主降落一体化实现时,自主降落策略复杂度尽可能低以保障计算资源、提升降落的成功率和精度。

针对以上问题,本文提出了面向空地协同无人机快速路径规划与自主降落一体化实现技术,基于扩展邻域搜索、改进启发函数和自适应权重的改进A*算法和基于ArUco码视觉反馈的无人机自主降落策略。仿真和实验结果表明,无人机可以在密集环境下快速完成路径规划,同时准确识别并精准降落到地面平台目标点上。

1 改进A*算法

1.1 传统A*算法原理

A*算法是获得静态环境中最短路径十分有效的搜索方法。A*算法的代价函数表示为

f(n)=g(n)+h(n)

(1)

式中:f(n)是从初始状态经由状态n到目标状态的最小代价估计;g(n)是从初始状态到状态n的最小实际代价;h(n)是从状态n到目标状态的最小代价估计。算法在扩展节点的过程中,每次选取代价函数最小的节点作为当前节点的下一节点,直至寻找到目标点。

传统A*算法虽然能够求解出路径的最优解,但当环境地图复杂、地图分辨率较高时,算法求解时间过长,实时性差;同时,得到的路径平滑性差,不利于无人机快速稳定飞行。为了满足空地协同场景中无人机实时快速路径规划需求,本文提出基于16方向扩展的搜索方式、改进切比雪夫距离的启发函数、自适应权重系数与贝塞尔曲线轨迹优化的方式,全面提升传统A*算法性能。

1.2 16方向搜索方式

传统A*算法扩展方式为8邻域搜索,无人机运动方向最小为45°,导致A*算法规划后的路径较为曲折、平滑度低,不利于复杂密集环境下无人机平稳飞行。本文将A*算法中8邻域扩展改进为16方向扩展的搜索方式,搜索原理如图1所示。

图1 A*算法不同搜索方式

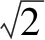
1.3 改进启发函数

传统启发函数主要由3种距离表示,即曼哈顿距离[15]、切比雪夫距离[16]和欧几里德距离[17]。在16方向扩展方式中,以上3种启发函数均不能准确反映搜索距离。为了适应和提高算法扩展效率,需要重新设计与16方向扩展方式相匹配的启发函数,提出的改进式启发函数定义为

(2)

式中:a=min(dx,dy),b=min(|dx,dy|,a),min表示取最小值,dx表示当前节点到目标节点X方向的距离,dy表示当前节点到目标节点Y方向的距离;c=max(dx,dy)-2b,max表示取最大值。

图2 不同启发函数示意图

不同启发函数表示时,最小代价估计h(n)的大小不同。其中,改进切比雪夫距离表示最小代价估计h(n)与最小实际代价g(n)的计算方式相同,确保一定能找到最优解。

1.4 自适应权重系数

将A*算法评价函数修改为

f(n)=g(n)+w*h(n)

(3)

(4)

其中:(XG,YG)为目标点;(XS,YS)为起始点;w为自适应启发函数权重系数。

采用自适应权重方式,可以同时兼顾搜索速度和规划路径长度。在搜索前半程,快速到达目标所在区域;在搜索后半程,增加搜索节点、降低搜索速度,得到最优路径。最后,通过贝塞尔曲线[18]对规划的路径做进一步平滑处理,提升规划路径的平滑度。

2 无人机自主降落策略设计

2.1 ArUco码识别与位置解算

为了确保无人机能够准确识别降落平台,本文采用基于ArUco码的目标识别方法。世界坐标系与像素坐标系定义如图3所示。世界坐标系原点Ow定义在二维码中心处,二维码边长为s,二维码4个顶点的坐标分别为A=(-s/2,s/2,0)T,B=(s/2,s/2,0)T,C=(s/2,-s/2,0)T,D=(-s/2,-s/2,0)T,它们在像素坐标系Oiuv中的坐标分别对应为a=(ua,va)T,b=(ub,vb)T,c=(uc,vc)T,d=(ud,vd)T。图3中,OeXeYeZe为相机坐标系。

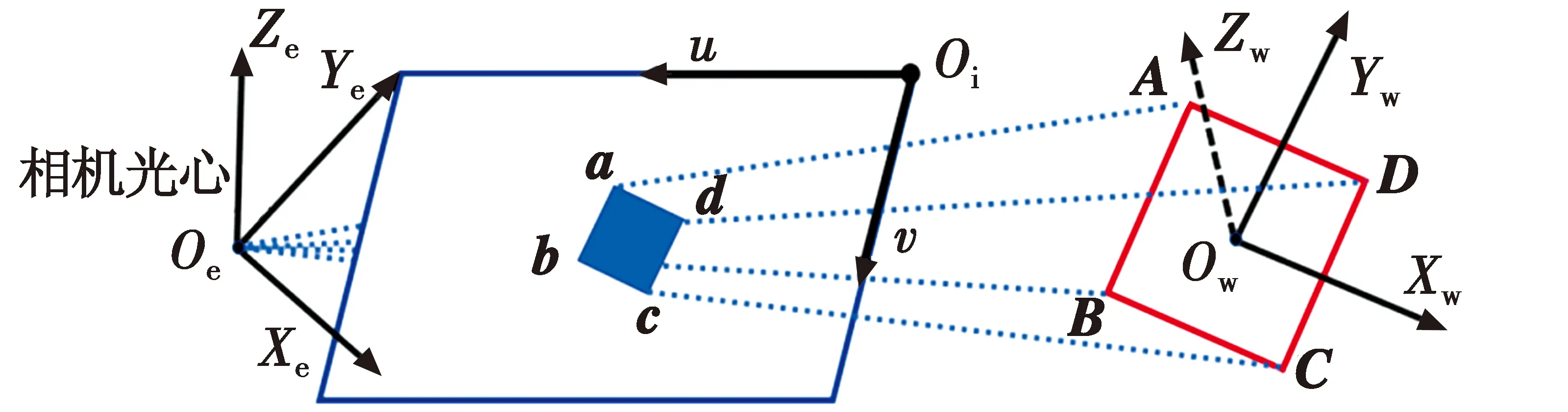
图3 世界坐标系与像素坐标系定义

由相机模型可知,三维空间坐标与像素坐标之间的转换关系(以A-a为例)为

(5)

式中:fx为相机坐标系中Xe方向的焦距;fy为Ye方向上的焦距;Cx为像素坐标系中u方向上的像素点的偏移量;Cy为v方向上的像素点的偏移量。fx,fy,Cx和Cy共同组成相机内参矩阵K。

令

(6)

(7)

2.2 自主降落控制策略设计

由2.1节可知,通过ArUco码检测与坐标变换,可以得到降落目标点在相机坐标系下的位置信息。本节介绍基于ArUco码位置反馈信息的无人机自主降落策略。假设在时刻t无人机位置PUAV(t)=(x(t),y(t),z(t))T,降落平台位置Pd=(x(dt),y(dt),z(dt))T,则无人机与降落目标点的相对位置误差为

ΔP=(Δx(t),Δy(t),Δz(t))T=(x(dt)-x(t),y(dt)-y(t),z(dt)-z(t))T。

(8)

依赖相对位置误差反馈信息,无人机自主降落策略设计为

VUAV(t)=(Vx(t),Vy(t),Vz(t))T

(9)

(10)

(11)

(12)

其中:Vx(t),Vy(t),Vz(t)分别为无人机在世界坐标系下沿Xw轴、Yw轴、Zw轴方向的速度;K11,K12为沿Xw方向速度控制系数;K21,K22为沿Yw方向速度控制系数;K3为无人机高度方向控制系数;h1为最低降落距离,当无人机与地面降落平台垂直方向距离小于h1时,无人机已经到达最低降落高度,进入飞控land模式。

在自主降落速度控制策略中引入了比例与微分控制可以提高自主降落策略的响应速度。无人机与地面平台相对位置如图4所示。为了确保地面降落平台始终在无人机相机的视角范围内,当高度差与水平面方向的距离之比过小时,Z轴方向速度为零,直至角度θ小于规定值,θ的大小由相机视角决定。无人机自主降落控制系统框图如图5所示。

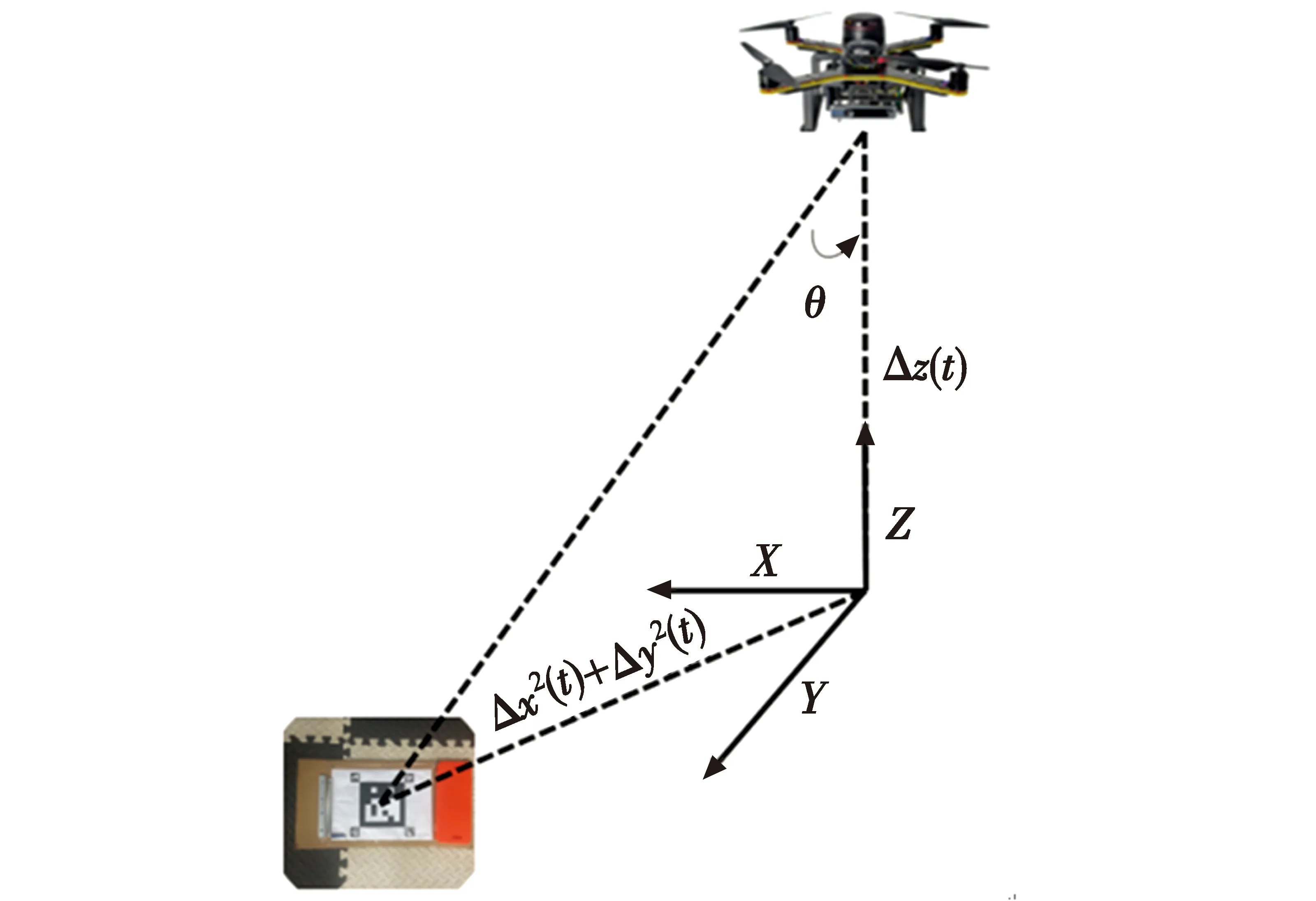
图4 无人机与地面平台相对位置

图5 无人机自主降落控制系统框图

进一步设计了空地协同自主降落精度指标E为

(13)

式中:(xcenter,ycenter)T为ArUco码中心位置坐标;(xult,yult)T为无人机在最终时刻的降落点位置坐标。

3 仿真与实验结果

3.1 改进A*算法性能分析

在Python3的离线环境下验证了本文所提改进A*算法的性能,结果如图6和表1所示。其中,方式1表示采用4邻域搜索与曼哈顿距离得到的路径,方式2表示采用8邻域搜索与切比雪夫距离得到的路径,方式1和2都属于传统A*算法;方式3表示采用16方向搜索与切比雪夫距离得到的路径,方式4表示采用16方向搜索与改进切比雪夫距离得到的路径,方式5表示在方式4的基础上加入自适应权重后得到的路径,方式6表示在方式5的基础上额外加入贝塞尔曲线处理后的路径。

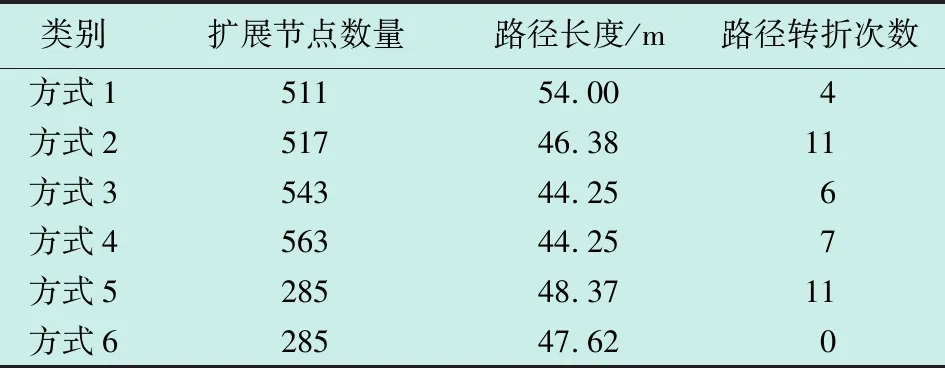
表1 不同搜索方式下A*算法性能对比

图6 不同搜索方式下A*算法规划路径的结果

从图6和表1可以看出,采取16方向搜索与改进切比雪夫距离相结合的搜索方式时,虽然扩展节点数量稍有增加,但是显著缩短了路径规划的长度;此外,相比8邻域搜索,路径转弯次数和转折角度大幅减小,规划路径平滑度大幅提升。方式5相比方式4增加了自适应权重系数,规划路径长度和转弯次数小幅增加,但算法运行速度显著提高,扩展节点数量减少了49.37%。综合来看,最终的改进A*算法(方式6)相比传统A*算法(方式1和2),扩展节点数量大幅减少,路径长度更短,转弯次数更少,路径更加平滑。

3.2 无人机路径规划与自主降落实验一体化实现

选用的无人机硬件组成包括Pixhawk 4飞控计算机、英伟达TX2板载计算机、英特尔T265双目视觉相机和200万像素单目相机以及思岚S1激光雷达。软件构成包括Ubuntu18.04,ROS melodic,Rviz和PX4。无人机软硬件系统构成如图7所示。

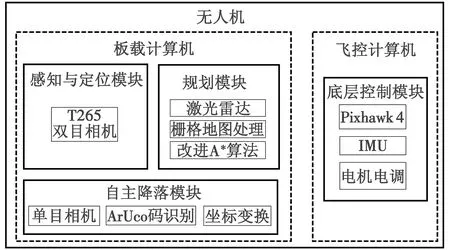
图7 无人机软硬件系统构成

实验结果如图8～11所示。在未知环境中,无人机通过激光雷达获得周围障碍物的点云信息,并实时将点云信息发送给无人机路径规划算法。由图11可知,无人机起飞并获得目标点后,由于场地障碍物较多,且激光雷达感知范围有限,无人机起飞后并不能获得全部地图信息,随着飞行过程中不断感知与完善地图信息,最终安全到达目标点。 图8(a)～8(c)和图9(a)～9(c)显示无人机规划出路径并飞行一段距离后,检测到由于障碍物阻碍无法到达目标点;图8(d)和图9(d)显示无人机根据现有环境信息规划出新的可行路径,改进的A*算法在处理地图上新出现的障碍物时能够迅速重规划,体现出很好的实时性和快速性;图8(e)～8(f)、图9(e)～9(f)显示无人机到达目标点后,开始执行自主降落指令并最终平稳降落到地面平台。图10(a)和图10(b)分别为实验中无人机位置和速度响应曲线。图11为无人机与降落平台的相对位置误差响应曲线,可以看出无人机降落误差不大于0.15 m,精度达到分米级别。

图8 Rviz中无人机路径规划及自主降落实验过程

图9 无人机路径规划与自主降落实验过程

图10 真机实验中无人机位置和速度响应曲线

图11 真机实验中相机输出无人机与降落平台的相对位置误差响应曲线

4 结束语

本文提出了面向空地协同场景下无人机路径规划与自主降落技术,一体化实现了无人机快速路径规划与平台精准自主降落功能。通过采用16方向扩展搜索、改进启发式函数和自适应权重方式全面提升了传统A*算法的性能;进一步地,设计了面向地面移动平台的基于ArUco码视觉反馈的无人机自主精准降落策略。仿真和实验验证了本文所提改进A*算法、自主降落算法和一体化实现策略的性能。结果表明:改进的A*算法具有更快的运行速度,规划出的路径长度更短,同时路径平滑度更好;自主降落策略能够保证无人机实现地面平台的精准快速自主降落。本文研究成果能够有效满足空地协同中无人机侦察、支援、回收等任务场景下快速路径规划与自主精准降落技术需求。下一步研究将聚焦在非协作陌生环境下无人机路径规划与自主降落技术。