基于改进NSGA-Ⅱ算法的双运输机重装空投研究

李 山, 权 文, 苏力德, 黄呈祥, 李晨昕

(空军工程大学,a.空管领航学院; b.航空工程学院,西安 710000)

0 引言

重装空投是指通过运输机将重型装备、设备快速投送到战场前沿、敌后方关键目标附近等区域的军事活动[1]。其凭借高机动性、高灵活性、大运量等特点,已成为现代战争的重要组成部分。但重装空投难度大、要求高、流程繁琐,目前仅有少数国家掌握该技术[2]。因此,发展重装空投技术,提升重装空投能力,对占据未来战场主动权至关重要。

如何将物资安全、准确、快速地投放到指定地点是重装空投任务重点考虑因素与难点所在。现阶段,有大量学者对重装空投中货台脱落过程[3-4]、运输机飞行控制[5-6]、货台着陆稳定性[7-8]等问题进行研究,取得了丰硕成果。但针对重装空投编队设置、货台落地散布控制的研究相对较少,在这方面主要还是依靠人工经验进行任务规划,存在较大主观性,空投精准度还有待提高[9]。

因此,本文将针对重装空投中典型的双运输机编队多目标规划问题,研究在两货台落地点与落地时间都尽可能近的双目标下,两机的最佳编队位置。构建双运输机编队空投模型,然后引入支配强度、优化精英策略、种群等级交叉系数、高斯变异算子和方差拥挤度,利用改进后的二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-II,NSGA-II)求解模型,最终结果证明了该算法的可行性。

1 基于分离法的单机空投货台运动模型

重装空投可以分为3个阶段:1) 牵引伞舱内带动阶段;2) 主伞打开,货台离开飞机货舱门,货台所受作用力由水平方向变为垂直方向;3) 货台进入稳定匀速下降阶段。空投过程中,虽然在第一阶段货台在舱内移动会改变载机的质心和转动惯量,但本文主要研究货台下落过程,即第2、第3阶段,而牵引伞的作用只是带动货台离开载机并拉出主伞,在货台下降阶段并不产生作用[10],所以本文模型不考虑牵引伞带动货台在舱内运动的阶段。本文变量均视为标量。

此外,考虑到风的影响,需要计算货台下落过程中受到的空气阻力f,算式为

(1)

式中:v为货台与风在对应方向上的相对运动速度;S为货台在垂直于风的来向上的受力面积;C为空气阻力系数;ρ为空气密度。ρ的计算方法为

(2)

式中:Pg为实际地面气压;P0为标准大气压;T为实际环境温度。将摄氏零度近似为273.15 K,考虑到空投是在低高度进行,货台下落过程中,周围温度变化不明显,因此,可将地面空投场的温度视作货台下落全过程的环境温度。

1.1 货台离开飞机货舱门至稳定匀速下降前

将该阶段货台运动分解为垂直和水平两个方向。

1) 垂直方向。

垂直方向货台二维运动方程为

(3)

2) 水平方向。

以空投场中心点(目标点)为坐标原点,以飞机进入方向为纵轴,以垂直飞机进入方向为横轴,建立二维平面坐标系XξOξYξ,如图1所示。

图1 水平方向坐标示意图

初始状态下货台水平速度表达式为

(4)

建立货台水平方向速度方程为

(5)

所以可得货台位置方程为

(6)

1.2 货台稳定匀速下降

同理,仍将该阶段运动过程分为垂直和水平两个方向。

1) 垂直方向。

当达到平衡状态时,货台所受合力为零,即有

(7)

式中,vH2为第2阶段货台的稳降速度。

设空投高度为H,则第3阶段的下降高度H3=H-H2,所以第3阶段的运动时间为

(8)

2) 水平方向。

易得,最后货台落点位置方程为

(9)

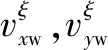
2 运输机编队规划模型

为使地面部队能快速定位空投物资,规划双运输机编队空投模型时,需要双机货台空投落点尽可能地接近。但由于飞机间会产生尾涡,其将对周围流场产生强烈的速度诱导作用进而导致处在其中的飞机发生滚转;且尾涡强度正比于飞机重量,运输机重量大、尾涡强,旋涡区切向的速度分量在旋涡形成后6～8 min才消失,严重影响后机飞行安全。故双机必须在保证安全的条件下,使得货台空投落点尽可能接近。

2.1 两机位置关系表达式

两机位置关系如图2所示。

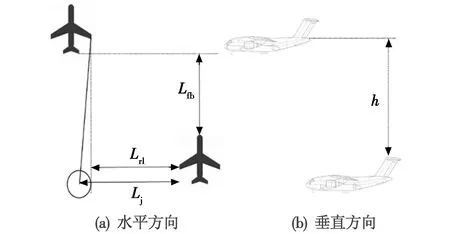
图2 两机位置关系图

以前机位置为坐标原点,构建坐标系XpOpYpZp,则后机坐标为(xp,yp,zp),其中,xp为两机左右间距,yp为两机前后距离,zp为两机高度差。设两机左右距离为Lrl,两机前后距离为Lfb,高度差为h(后机高于前机时为正)。两机空间前后距离d的算式为

(10)

2.2 尾涡影响模型

尾涡又称尾流,是指运动物体后方或下游的紊乱旋涡流。当后机进入前机的尾涡区时,会出现飞机抖动、下沉甚至翻转等现象,处置不当将会发生严重飞行事故。因此,飞行时应避免进入前机尾涡区。

何晏父亲早亡，曹操娶了他母亲尹氏为妾，尹氏把何晏也带进了曹家，这种不太合常理的事情，也只有曹操做得出来。

定义涡核半径rw,涡核间距Lw,则尾涡最大强度为

(11)

式中,G为飞机所受重力值。尾涡圆周切线速度最大值为

(12)

则根据双机位置空间表达模型得到前机尾涡完全形成距离为

(13)

式中:Cy为升力系数;λ为尾涡间距,本文取λ=5.448。

当飞机速度为vp时尾涡下沉高度为

(14)

后机所在截面距尾涡中心横向距离Lj为

(15)

后机距尾涡边界直线距离为

(16)

将圆周切线风速经验计算公式近似表达为尾涡衰减到后机翼尖的强度,即

(17)

2.3 目标函数和限制条件的确定

为便于地面部队定位货台、更快地处置空投物资,以两货台落地点间隔Δx、落地时间间隔Δt尽可能小为目标,建立目标函数为

(18)

为保证重装货台与飞机安全,要求货台所受尾流的切线风速影响不超过安全值vs,高度差不小于尾涡下沉高度的负值,左右距离不得进入尾涡边界,前后必须保持一定距离。因此,可得限制条件为

(19)

3 基于改进NSGA-Ⅱ算法的模型求解

3.1 NSGA-Ⅱ算法概述

20世纪90年代初,印度科学家SRINIVAS和DEB提出了一代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)。2002年,DEB在NSGA基础上提出了NSGA-Ⅱ算法,降低了NSGA算法的计算复杂性,并且无需确定共享参数,一定程度上提高了算法的鲁棒性和计算效率[11-12],算法流程如图3所示。

图3 NSGA-Ⅱ算法流程图

显然,该空投模型是一个典型的多目标优化问题(Multi-objective Optimization Problem,MOP)。目前,解决此类问题的方法主要有粒子群算法[13-14]、蚁群算法[15-16]、基于分解的多目标进化算法(Multi-objective Evolutionary Algorithm based on Decomposition,MOEA/D)[17-18]和遗传算法(NSGA)[19]等。由于遗传算法具备较强的全局搜索能力、精度高,有利于降低双机队形的细微偏差所带来的任务风险,并且其不仅适用于连续变量,而且可处理非连续变量,如果后期考虑到空投物(如坦克、步战车)形状等非连续变量,需对模型进行调整改进,该算法也有很好的兼容性。因此,本文利用其对模型进行求解。但传统NSGA算法存在高计算复杂性、需人为指定共享参数等问题,而改进后的NSGA-Ⅱ算法使用快速非支配排序、拥挤度比较算子以及精英策略,降低了算法运行复杂度,同时有效减少了最佳个体的损失,提高了算法鲁棒性,可以很好地克服一代算法的不足。然而,二代算法同样也存在着局部性收敛、种群多样性较低等问题,运算精度离重装空投的要求依旧存在差距[20]。因此,为了进一步提高模型计算效率并使模型更贴近于实战需求,本文将按照NSGA-Ⅱ算法流程,根据现有算法步骤中存在的不足改进算法。

3.2 改进NSGA-Ⅱ算法流程

根据上述NSGA-Ⅱ算法及不足,本文对传统算法进行改进,流程如图4所示。

图4 改进后的NSGA-Ⅱ算法流程

1) 初始种群产生。

根据自变量,随机选择若干个初始解作为算法搜索起点P0。

2) 确定适应度函数。

通过每个个体的适应度来评定每个个体的优劣程度,进而决定其遗传概率的大小。

3) 基于支配强度的快速排序法。

传统NSGA-Ⅱ算法采用的非支配排序方式可能会导致较多伪非支配解的产生,对最终解集的质量产生不利影响。因此引入支配强度(种群优越性指标)θ,即

(20)

4) 基于方差的拥挤度计算。

传统的拥挤距离计算方法只考虑了相邻个体间的间距,使得群体间的拥挤距离差别越大,获得的遗传机会却越少,从而不利于解的平均性分布。因此引入方差因素来优化解的分布,即

(21)

5) 选择。

6) 基于个体种群等级的交叉算子。

7) 基于高斯分布的变异算子。

Xj2=Xj1+γ(Xmax-Xmin)

(22)

式中:γ为一个随机数,且该随机数满足高斯分布;Xmax和Xmin分别为Xj的上边界与下边界。

8) 优化精英策略。

传统的精英策略最终是保留所有的精英个体,可能会导致算法收敛于局部。本文引入优化精英策略:确定比例c,将N×c个个体纳入到下一代种群中,如果数量不足,可从第二最优层中选取,剩余的N×(1-c)个个体再从次优层中选取。通过此方法可以有效解决提前收敛的问题。

3.3 模型求解

假设某次重装空投任务相关参数如表1～3所示。

表1 风向和风速

表2 地面环境参数

表3 运输机飞行参数

计算结果如表4、表5所示。

表4 算法优化前后空投编队位置对比

表5 算法优化前后空投效果对比

从表4可以看出,算法优化后两机前后距离增加了19.6 m,左右间隔增加了11.3 m,两机高度差扩大了102.8 m。相较于原算法,两机之间的飞行间隔更大,前机尾涡对后机产生的不利影响减小,编队飞行安全性提高。

同时,对于重装空投而言,为了安全起见,地面部队一般需等空投物资全部落地之后方可前往空投点。由表5可知,本文算法算得的落地时间间隔缩短了18 s,因此地面部队的等待时间减少了;且优化后算法求得的落地间隔减小了16.4 m,落地点分布更加密集,使得地面部队能更加集中地、更快地领取所有的空投物资。可见,优化后算法的空投效果更好。

从飞行安全方面和目标实现两方面综合分析,改进后的算法性能总体上优于传统算法。

4 结束语

本文基于分离法和欧拉迭代公式,就双运输机空投编队规划问题建立通用数学模型,构造出编队规划约束函数,在模型求解时引入支配强度、优化精英策略、种群等级交叉系数、高斯变异算子以及方差拥挤度对NSGA-II算法进行改进。最终结果表明,本文算法所得的双运输机编队空间分配位置合理、空投效果较好,性能优于传统算法。该模型可有效辅助指挥员规划运输机重装空投任务。