跨流域跨声速平板绕流计算研究

姚思齐

(北京航空航天大学 北京 100191)

高超声速飞行器的整个飞行阶段涉及连续流到自由分子流整个流域范围，是典型的跨流域流动问题，需要考虑局部的稀薄气体效应、可压缩效应、粘性效应和非平衡效应的共同作用。全面分析跨流域高超声速流动的特点，准确预测流动的气动力与气动热，具有重要的理论价值和实际意义[1]。

平板绕流作为流体力学中最经典的问题之一，经常被作为理论分析的研究对象[2]。BIRD G[3]研究了Knudsen（Kn）数在0.1～10 的高超声速平板的气动特性，结果表明随着Kn数减小，与平板碰撞分子增多，平板表面的剪切应力也随之增大。胡远等人[4]结合了计算流体力学（CFD）方法和直接模拟蒙特卡洛（DSMC）方法进行模拟，研究了超声速平板绕流的全流域阻力特性。HUANG A等人[5]最早通过求解BGK模型方程，对高超声速前缘尖端的平板绕流问题进行了研究，得到了流场速度、温度、压力和密度等流场宏观量。

本文采用基于SPARTA平台开发的USP[6-7]算法的求解器SPARTACUS[8]，针对典型的高超声速平板绕流问题进行研究，分别以来流马赫数（Ma）和Kn数为参数，研究来流变化对流动传热的影响；并针对主要关注的平板阻力系数进行分析。

1 计算参数设置

平板绕流示意图如图1所示，平板的长度为0.1 m，起始位置在归一化坐标的原点处。平板的厚度为0.005 m，温度为Twall=300 K，完全漫反射边界条件。由于平板绕流问题是关于水平方向轴对称的流动，采用对称边界条件，仅考虑平板上半部分的流场。流场左侧和上方为入口，来流气体分子从左侧水平方向过来，右侧为流场出口。来流的工质为单原子气体——氩气，温度为T∞=300 K，分子碰撞模型选择变径软球模型（VSS），粘性指数（ω）为0.81，参考直径（dref）为4.11×10-10m。笔者以Knudsen 数和Mach 数作为分析对象，Kn为0.02、0.2、2、20，Ma为2、5、10、20，计算流域从滑移流域到自由分子流，流速从超声速到高超声速。本文针对粒子密度较高且宏观量变化梯度较大的区域进行网格加密，从而能够实现对流动传热的准确捕捉。

图1 高超声速平板绕流示意图

2 流场结果分析

2.1 流场密度分布

图2为流场无量纲密度数值模拟的结果。为了方便展示，这里给出了代表性的计算结果，Kn=0.02 和20，Ma=2 和20。在近连续流超声速流动中，边界层的影响导致出现斜激波，从平板前缘附近向下游发展。在边界层内，由于靠近壁面的连续流无滑移或滑移流域速度滑移条件，从外部无粘流动到近表面流动会出现速度和温度梯度。由于边界层内的粘性效应，流体在外部无粘流动和粘性区域之间进行质量、动量和能量的交换。当超声速来流在粘性区域内流动时，流体受到压缩，前缘产生压缩波并收敛形成激波。当超声速气流通过斜激波时，流线发生偏转，流体密度增大。

图2 不同参数下的平板绕流密度云图

激波的厚度大致相当于分子平均自由程的几倍。连续流中的激波在流场中产生不连续结构，激波前后物理量跳跃。事实上，在平均自由程的尺度内，激波中会有剧烈的质量、动量和能量的输运，尽管这个尺度对于连续流来说太小。在激波内，流体处于强非平衡状态，流体的熵会通过激波增大。激波结构内部的现象需要从分子动力学理论的角度来描述。

随着来流Kn数的增加，激波厚度也随之增加。在连续流中，非连续激波与边界层之间应存在无粘性区域。对于滑移流动，激波开始与整个平板上的边界层合并，变得难以区分。在自由分子流中，不存在典型的激波结构，密度通过壁面扰动（特别是来自前缘的扰动）连续变化。在近连续统区，激波沿前缘向下游的发展大致呈线性，而在自由分子流区，激波沿前缘向下游发展的区域大致呈线性，扰动影响逐渐减小，形成弧形区域。低马赫数（Ma）时，扰动集中在前缘，随着马赫数（Ma）的增加，扰动逐渐向下游和靠近壁面移动。激波强度随Kn数的增加而逐渐减弱，波后的密度变化明显减小。

马赫数（Ma）可以反映流动的压缩效应强弱。对于气体的流动，可压缩性对气体的密度、温度和压力分布有显著影响。随着马赫数（Ma）的增加，激波角度减小，激波层变薄，这在滑移流区中可以明显观察到。对于自由分子流区，在马赫数（Ma）为2时，扰动主要集中在前缘，而在马赫数（Ma）为20 时，扰动逐渐向壁面靠近并覆盖整个平板区域。激波强度随马赫数（Ma）增大而增大，激波密度随马赫数（Ma）增大而增大。

在马赫数（Ma）为2时，流场的最大密度位于激波后和前缘附近，见图2（a）。对于滑移流动，随着马赫数（Ma）的增加，最大密度位置沿激波逐渐向下游移动。这是因为随着马赫数（Ma）的增加，激波角减小，激波与边界层合并的区域变大。在合并层中，流体的密度和压力会由于边界层内质量和动量的交换而降低。对于自由分子流，随着马赫数（Ma）的增加，最大密度的位置会向壁面靠近。原因是对于高超声速流动，来流的总温度远高于300 K的壁温。由于墙体的冷却作用，密度会明显增加，并在壁面附近形成高密度区域。

为明确投资量的影响，回归分析多个港口的固定资产投资和泊位能力的数据，得到根据固定资产计算泊位能力的公式。然后，基于泊位能力与其他设施指标(如装卸设备、存储能力等)间的关系，确定投资对港口竞争力的影响。设泊位长度与其他q个基础设施指标间的配比率为g，则单位固定资产投资与基础设施指标的关系为

2.2 流场马赫数（Ma）分布

流场马赫数（Ma）分布的数值模拟结果如图3 所示。气体流经激波后会被压缩和减速，近连续流Kn=0.02 中激波前后的马赫数可用斜向理论描述，激波的后面，在远离表面的地方有一个粘性区域，在靠近平板的地方有一个低速区，这就是边界层。边界层内的流体受外部无粘流动的驱动，受到壁面阻力的约束。因此边界层内存在剧烈的动量输运，可以看出壁面附近存在较大的速度梯度。

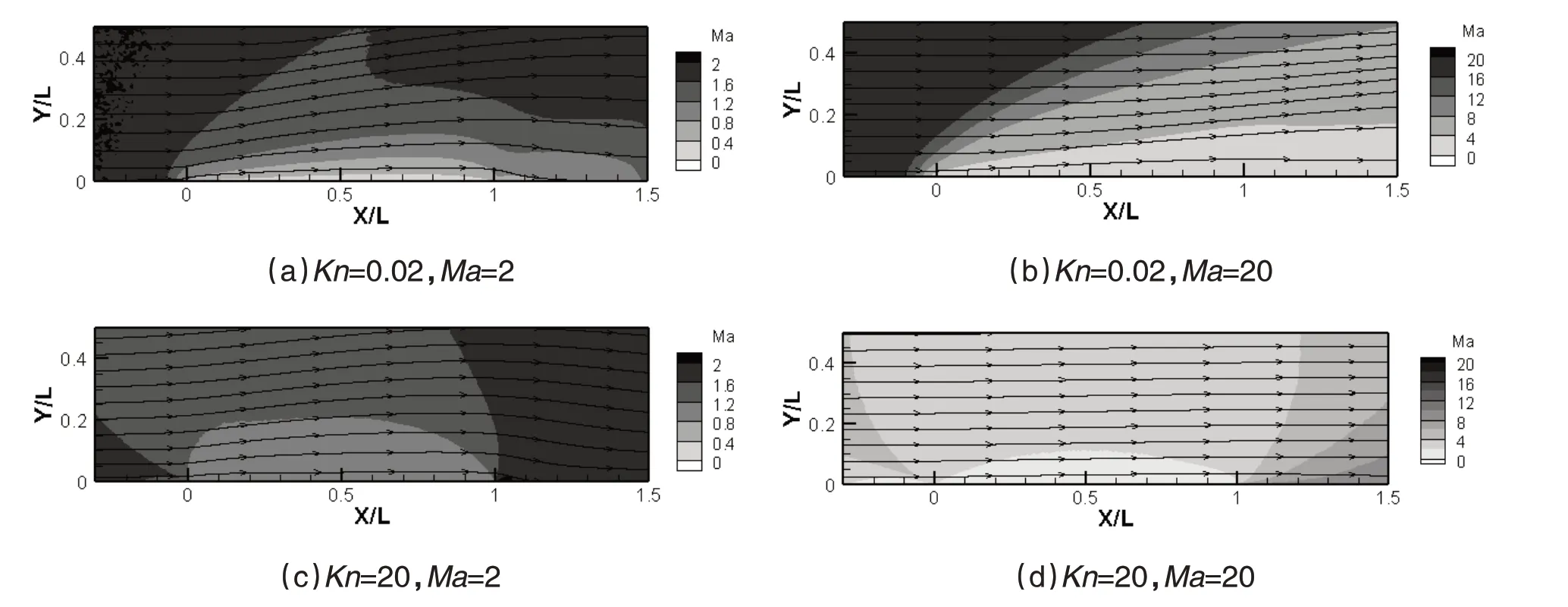
图3 不同参数下的平板绕流马赫数云图

在平板末端，边界约束消失，但外部流动与来自边界层的低速之间仍然存在梯度，因此由于粘性效应，产生自由剪切流动。后缘附近有3层，即无粘性外流层、边界层和粘性层。子层与附面层相遇后，出现尾流，这是一种受来自子层的低速无粘流驱动的自由剪切流。边界层和尾迹的厚度随着马赫数的增大而增大，马赫数越大，雷诺数越大。壁面附近的速度明显不为零，这是速度滑移现象。滑移速度随Kn数的增加而增大，速度梯度减小，剪切应力减小。

2.3 流场温度分布

图4为流场无量纲温度的数值模拟结果。总温度取决于来流马赫数，激波前后的总温度保持不变，这是能量守恒的结果。因此，来流总温度可以用来表征整个流场的总能量。由于激波的减速和边界层动量的耗散，流动的动能会转化为焓。对于高超声速流动，壁面附近的静态温度可以高达数十倍，显然，这将在壁面附近产生较大的温度梯度，并产生巨大的对流热流。

在滑移流Kn=0.02 时，仍然可以观察到典型的激波结构，激波结构从前缘到下游大致呈线性发展。在Kn=20时，平板对气体流动的扰动向上游传播，在平板前缘上游相当大的区域温度分布与来流不同。特别是Ma=20，有两个区域温度非常高，一个在靠近壁面处，另一个在前缘正前方。前者是由于壁面的减速作用引起的，后者是由于前缘的阻碍作用造成的。对于连续介质流动，前缘扰动在高超声速流动中直接向下游传播，而对于稀薄流动，前缘扰动可以像在亚音速连续介质流动中一样向上游传播。随着Kn数的增加，高温区向下游延伸，甚至覆盖整个平板。随马赫数（Ma）增加，高温区向壁面移动。

3 平板表面参数研究

图5 为平板上表面摩阻系数的数值模拟结果，表面摩阻系数Cf为

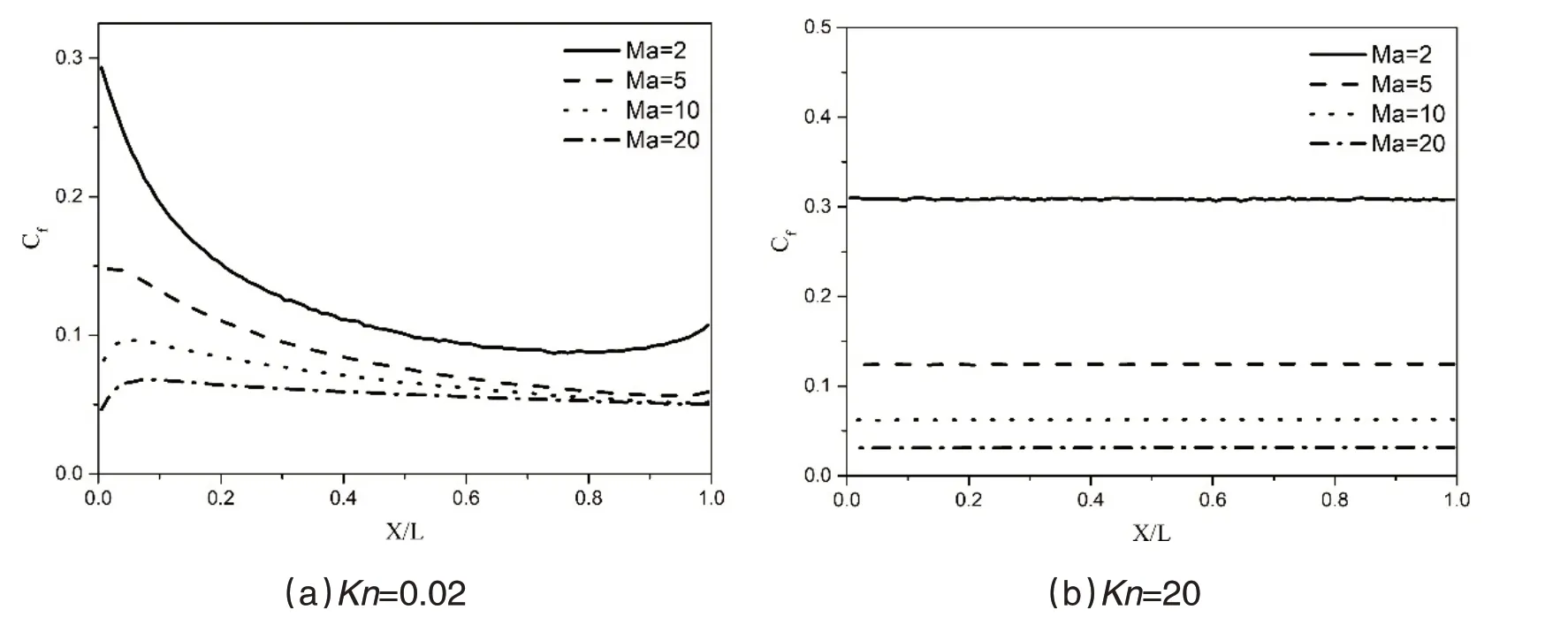
图5 平板上表面摩阻系数

随着Ma1增大，激波角减小，流线偏转更剧烈，从而Ma2增大，但压缩性或激波强度增加会使Ma2减小更明显。因此，流马赫数越大，激波后速度梯度越小，摩擦力也就越小。

如图5 所示，在近连续流Ma=2 时，摩阻系数沿板先减小后增大；而高马赫数时，前缘附近会有一个局部最大值。这是前缘局部稀薄效应作用的结果。随着马赫数增加，激波强度增大，密度梯度增大。由局部Kn数定义可知，前缘附近的局部稀薄效应会使马赫数增大，导致速度滑移增大，速度梯度变小。因此，离开稀薄效应的非平衡区域后，摩擦在前缘附近减小，沿平板方向增大。

一般情况下，稀薄条件下的摩阻系数要大于近连续流条件下。随着Kn数的增大，摩阻系数沿平板方向的变化更为平缓，这是由于稀薄气体效应的范围扩大到整个平板。对于自由分子流，平板对流动的影响在壁面的任何位置都是相同的，因此摩阻沿平板不会发生变化。对于自由分子流动，摩阻系数与来流马赫数成反比，这与自由分子流动理论给出的结果是一致的：

图6为平板上表面的压力分布，压力系数（Cp）为

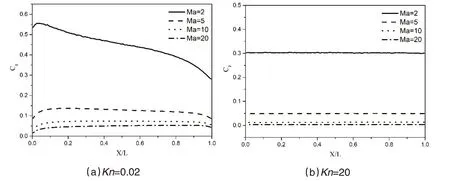
图6 平板上表面压力系数

一般情况下，压力系数随马赫数的增加而减小。如图6（a）所示，前缘附近存在局部最大值，这也是产生稀薄效应的原因。一般来说，稀薄流动的压力系数要大于近连续流动的压力系数。随着Kn数的增大，压力系数沿平板变化的趋势逐渐缓和。压力系数也与来流马赫数成反比，这与自由分子流动理论给出的结果一致：

图7为平板上表面的热流系数，热流系数为

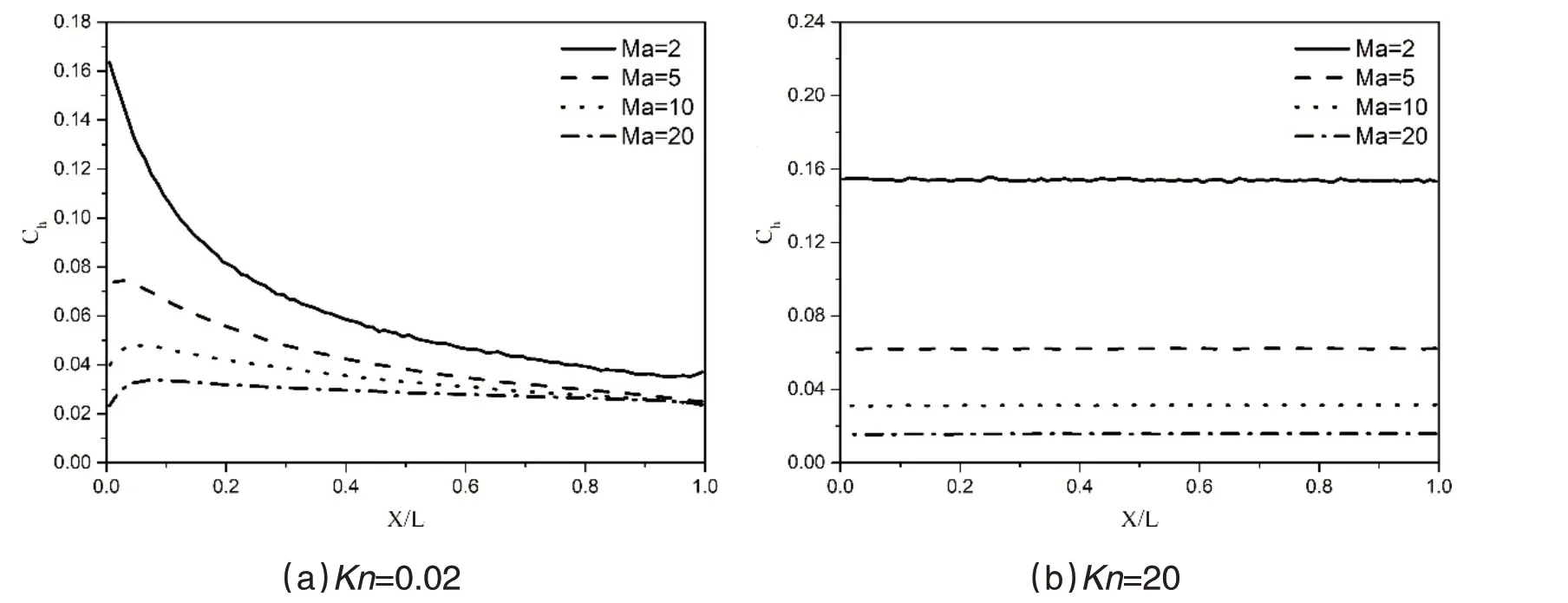
图7 平板上表面热流系数

当热流系数约为摩阻系数的1/2时，这不仅适用于任何马赫数的稀薄流动，而且还适用于近连续流流动（Ma>5）。

平板阻力是工程应用中最关心的气动特性参数，通过对摩阻系数沿表面积分得到：

式（7）中，Cf,up和Cf,down分别为上下表面摩阻系数，对于零攻角平板则有Cf,up=Cf,down。在实际应用中，一个简单准确的阻力计算公式有非常重要的价值[9]。对于跨流域跨声速平板绕流问题，需要同时考虑马赫数和努森数的影响。针对低速平板绕流，樊菁等人[10]提出了阻力计算的桥函数公式：

式（8）中，CD,C和CD,FM分别为摩阻系数的连续流和自由分子流解。桥函数是利用连续流和自由分子流的气动特性，对过渡流的气动特性进行插值预测。对于连续流，胡远等人[4]根据分析得到了高超声速平板绕流的摩阻表达式：

对于自由分子流，同样给出了拓展到过渡流域的公式：

把式（9）和式（11）带入桥函数式（8）中，就可以得到不同参数下的平板绕流阻力系数，具体如图8所示。研究了马赫数从2～20变化的几组数据，与通过USP方法模拟得到的结果进行对比发现，USP 方法计算得到的跨流域跨声速平板阻力系数与桥函数的计算结果吻合的较好。

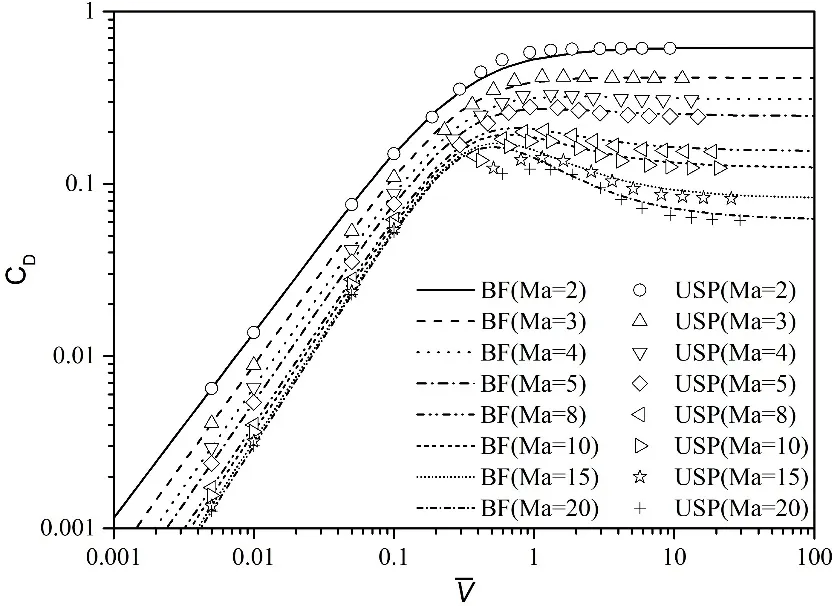
图8 跨流域跨声速平板阻力系数

4 结语

本文基于能够处理跨流域复杂流动传热问题的多尺度粒子USP方法，通过开发后的SPARTACUS求解器分析了典型的高超声速流动，对跨流域跨声速条件下的平板绕流问题进行了系统性的流动特性分析；并结合固壁表面的摩阻、热流及压力系数进行研究。结果表明：随着马赫数增大，压缩效应导致激波厚度减小，平板表面的摩阻系数热流系数都相应的增大；随着Kn数增大，分子间碰撞不充分导致更多的气体分子与壁面发生碰撞，形成了局部的高温高压区域。结合阻力系数计算的结果与桥函数公式进行对比，结果吻合得较好。