基于Hibbard算法的改进型插值算法

张烁晨

(西安交通大学 陕西 西安 710049)

彩色相机的发展已经有几十年的历史，早期的彩色相机的成像过程是在镜头前加装三原色滤光片，依次拍3张照片，然后合成1张彩色照片。但这种方法具有成像模块体积较大，三色图片难以完全匹配等缺陷，如今只有航空航天等少数领域还在使用这种成像方式。随着成像技术的进步，相机的体积显著缩小，同时为了满足摄像的便携性，也必须采用一次成像的方法得到图像，早期的光学彩色相机已经不适合应用于商业。于是出现了适应一次成像的照相方式，其成像原理类似于生物视网膜，即将三原色的感光单元密布在一张底片上，同时获取3个颜色的信息[1]。一个点的位置只能放入一个感光单元，因此只能记录一个颜色的值。而倘若直接把邻近位置的颜色放在一起，就会产生相差，因此需要通过一定的手段来消除相差[2]。数码相机出现后，出现了数字化的处理方式，即利用计算机对相邻点进行插值处理，以还原像素点内缺失的颜色通道值[3]。随着近年来数码相机的发展，数字化处理设备的普及，人们获取彩色照片的方式越来越便捷，数字化的成像技术已经发展成为了一门成熟的产业，与之相关的软硬件开发层出不穷。

受到缩小成像模块体积与减小成本等因素的限制，当今的彩色相机一般都只有一个感光片。感光片上密布着可以感知光强的小传感器，通过在感光片表面覆盖一张具有特定色彩排列的滤光片（Color Filter Array，CFA）得到原始图像[4]。这样得到的原始图片中，每一个像素点内只能记录一种颜色的光强。这种原始图片其实是一张由三色像素交错构成的矩阵阵列。不同排列格式的CFA如图1所示。

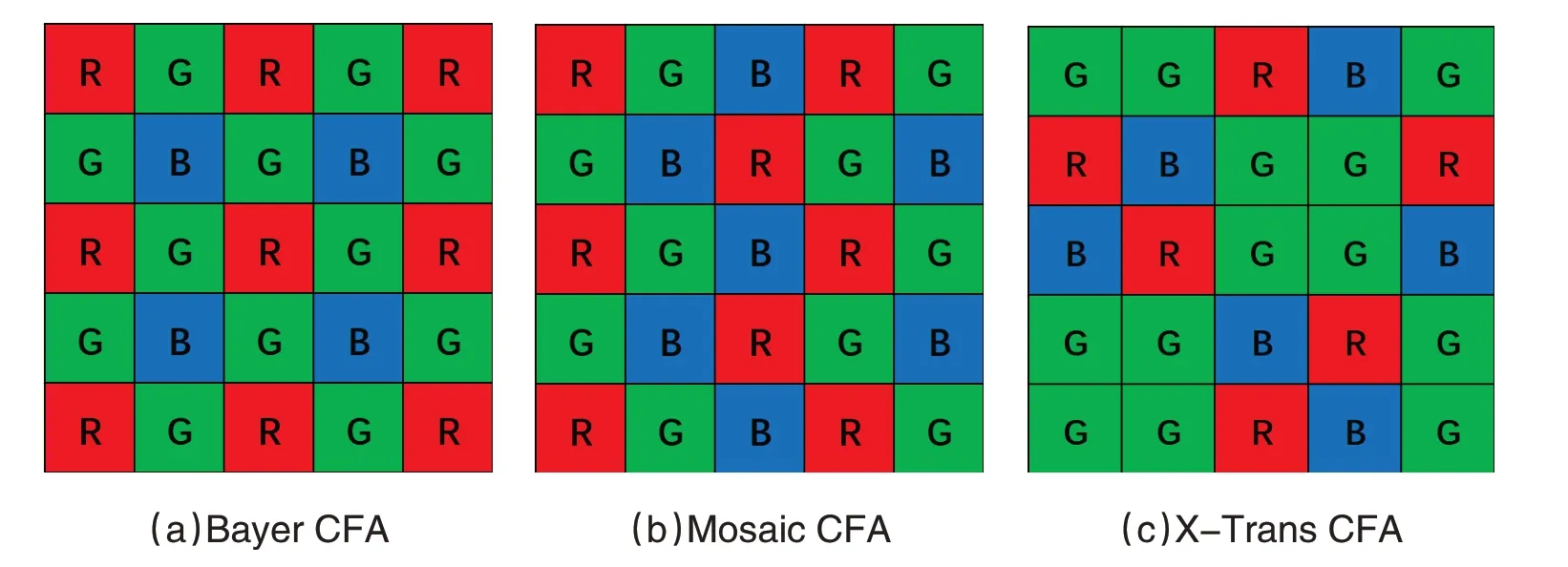
图1 不同的CFA阵列

通过对邻域内包含特定颜色的像素进行插值，进而还原某一像素点内缺失通道的色彩值，这种过程称为去马赛克（Demosaicing）处理[5]。不同CFA 阵列的适合场合不同，在同一场合的表现也各有优劣。如今主流的CFA 采用的是具有Bayer 阵列的滤光片。针对不同阵列的Demosaicing 算法有很多，也不尽相同；基于Bayer阵列的插值算法有双线性插值算法、样条插值算法、Cok算法、Hibbard算法等[6]。

由于Demosaicing 算法的性能直接影响了最终图像的还原效果，因而在硬件条件不变的情况下，研究更优秀的、更适合图片的算法则可以有效地提升成像的质量。现行的算法在遇到色彩值剧烈变化的区域，以及图像的边缘处，普遍会出现不同程度的颜色失真和拉链效应，使图片出现噪点[7]。本文提出了一种基于Hibbard算法的改进型插值算法，对RGB三通道先取对数处理，再进行插值，得到总亮度的修正量，最后对Hibbard算法进行亮度修正。相较于原算法，本文的改进算法对于图像色彩暗淡部分的恢复更加清晰，适用于对不明亮图片的还原，且改进算法的结构较简单，具有一定的应用价值。

1 对数插值算法

传统的Hibbard 算法对G 通道的还原采用梯度判别法，对梯度较小的通道使用线性插值方法。而线性平均应用于某些亮度较小的区域后，边界像素的还原值会被暗色背景拉低，导致很多细节处的亮度偏小[8]。而对数函数在其定义域上斜率很小，能够在一定程度上消除暗色背景对总亮度恢复的影响。如果先取对数再求平均，则边界亮度的还原值将会比线性平均更高，具体情况详见图2。

而在高亮度部分，由于通道颜色值较大，因而在取对数后，均值与原值的差异将不会很显著。

基于Hibbard 算法，对RGB 三通道均进行取对数处理，如式（1）所示：

如果单纯取对数再求平均，此时相当于取几何平均。注意到对数函数在其自变量值过小时反而斜率很大，因此可以预见对暗色部分进行还原时，反而会产生较大的偏差。而通道颜色值的取值范围是0～255，因而这种情况完全有可能发生[9]。所以引入一定的偏移量（本文采取+e3，以确保数据处于平缓区间），再进行插值，如式（2）所示（以行方向为例）：

此时对数函数在其定义域上就是相当平缓的，求平均值时可以使两点色彩值的贡献更接近，避免出现阴暗背景干扰边界插值的情况。

Hibbard算法在还原时具有一定色差，这是算法的固有问题[10]。实验结果表明：单独采用对数插值时，Hibbard 算法原有的色差会被一定程度上放大。这说明对数插值虽然在亮度的还原上具有优势，同时也具有放大色差的副作用。

为消除这一副作用，同时保持还原效果，本文采用将对数插值算法和Hibbard 算法相融合的方法。具体思路为：分别采用对数插值和Hibbard算法对图片进行还原，生成两张图像；再用对数插值图片在每一个像素点的总亮度值替换Hibbard 算法对应像素点处的总亮度，得到合成图片的通道色彩值。由于对数插值并未改变Hibbard算法的基本结构，即G通道插值方向的选取，以及R，B通道以G通道为基准进行还原；只是将具体的插值公式进行改变，因而图片在每个像素点仅有亮度与色差的差别，对应的像素点在匹配度上则没有任何差异[11]。因此可以只保留对数插值图片的总亮度值（记为Ω0），而不采用其颜色比例。再用得到的总亮度去修正Hibbard算法对应像素点处的总亮度，同时不会产生像差，如式（3）所示（以G通道为例）：

式（3）中，G'(i,j)为合成图片在某一像素点处的绿色通道的值，G(i,j)为Hibbard算法在该点处绿色通道的值，Ω与Ω0分别为Hibbard 算法与对数插值在该点处的总亮度值，总亮度由式（4）计算得到。

这样就得到了颜色比例与Hibbard算法一致，但总亮度值与对数插值算法一致的合成图片。在实际应用时应当注意避免分母Ω过小的情况，即在赋值前须事先规定Ω大于一个小量（如取Ω>1）时才能进行赋值。同时也可以这样理解：当Ω非常小时，说明该区域是近乎没有亮度的，即黑色区域，因而去掉这些无信息的像素点对图像恢复不会产生影响。融合算法既保留了对数插值在亮度还原上的优势，又保留了Hibbard算法在颜色比例的还原上的优势，没有出现色差放大的情况。

2 实验结果与分析

为检测算法的还原程度，本研究采用均方误差（Mean-Square Error，MSE）的方法来评价还原图像与原图的差异水平。如果一张图片规格为M×N，其均方误差的值为SMSE，则SMSE的定义为

其值越大，说明图像与原图的偏离度越大。如果选取待检偏差值为绿色通道的颜色值，此时f[m,n]的定义为：

表示原图像在特定通道的颜色值。而如果选取待检值为总亮度，则f[m,n]即为

f͂[m,n]的定义类似，表示还原图像在该通道的颜色值。

本文选取了10张背景较暗且细节较丰富的图片，分别计算双线性插值算法、Hibbard算法与对数插值算法的总亮度SMSE值，数据具体见表1。

表1 不同算法总亮度的MSE对比

在表1 中未列入融合算法的总SMSE值，因为融合算法正是保证了总亮度和对数插值一致，故二者SMSE相同。可以观察到，对数插值算法在大多数情况下，对亮度的还原效果要显著优于双线性算法。在一些细节较多的图片中，对数插值算法对亮度的还原要明显优于Hibbard 算法，而在一些色彩值变化不显著的地方，也与Hibbard算法的还原结果相近。

为评价算法对图像颜色还原的偏离程度，本文使用R、G、B 三色通道SMSE之和的值来衡量，数据如表2所示。

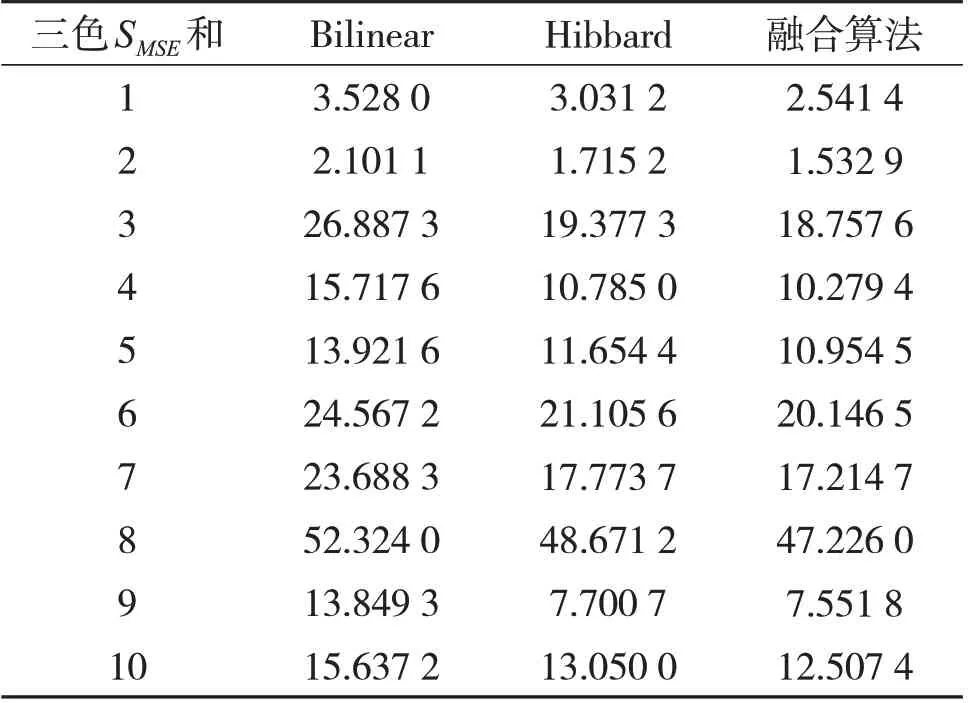
表2 不同算法的三色MSE总和对比

从表2可以观察到，在大多数情况下，融合算法对颜色还原的效果要明显优于Hibbard 算法。这主要是因为Hibbard算法在还原时只采用了线性插值方法，因而损失了一定的亮度值。融合算法在并未改变颜色配比的情况下，SMSE总和的值仍然低于Hibbard 算法，说明Hibbard 算法对图片的还原过程中确实是损失了一定的亮度值的。此次实验还发现，在一些主题为星空的图片中，融合算法普遍能够比Hibbard 算法的MSE值提升10%～20%，主要是因为图片所含的白色小点较多。这些只有几个像素大小的小点的还原，是很多以线性插值为基础的算法的劣势，背景对亮度的拉低作用将会十分明显。而本算法在处理这些细节时有一定的优势，图片所包含的这种点越多，SMSE的提升越明显。本次实验使用的10张图片如图3所示。

图3 本次实验使用的图片

综合表1、表2 可以看出，融合算法对于亮度的恢复效果是比较明显的，可以说同时兼顾了对数插值算法和Hibbard 算法的优势。由于亮度值和对数插值算法一致，因而总体SMSE和对数插值相等；同时颜色的还原比例又与Hibbard算法相同，因而不会放大色差。下面以一张细节较多的星空背景图片为例，放大某一局部，可以对比一些细节的还原结果，具体结果见图4。

图4 本文改进算法与Hibbard算法还原细节的对比

图5（a）是Hibbard算法的还原结果，图5（b）是对数插值算法的还原结果，图5（c）是融合算法的还原结果。对比观察可以发现：对于低亮度部分，对数插值算法在细节处的还原比Hibbard算法更清晰，主要是因为对数插值使得色彩值都向均值中心集中，还原后亮度值相比Hibbard算法要更高，但色差的放大也相当明显，可以看到图片整体发红。而融合算法则无这一缺陷，可以看到融合算法的亮度相较于Hibbard算法有所强化，但同时又保留了原始Hibbard算法的颜色还原比例，因而并未出现色差放大这一副作用。效果上低亮度部分的细节处看起来更亮，观感上更清晰；而在高亮度的局部，本算法的插值结果则和Hibbard算法相近，图像在整体上仍然保持了较好的还原效果，如图5所示。

图5 不同算法对高亮度图片的还原结果对比

3 讨论

在Hibbard算法对图片进行还原时，会产生一定的色差。这是两个因素共同作用的结果：一是由色彩值的剧烈变化所致，这是Hibbard算法在处理大梯度色彩值时的固有缺陷；二是由于基准颜色选取为绿色，对其他两个颜色通道的还原存在一定的误差[12]。大多数算法都不可避免地存在色差，一般而言，算法所使用的插值函数越复杂，就越容易放大色差，因此必须考虑减小色差或者消除额外色差的问题。本算法由于并未改变Hibbard算法的基本结构，于是也存在一定的色差。当单纯采用对数插值时，由于低亮度通道的颜色值得到了强化，因而色差也被一定程度上强化了。例如：很多以绿色为基准颜色的算法，还原图片就容易产生偏暖色的色差，而在进行取对数操作后就看起来会更红。本文采取的将Hibbard算法与对数算法融合后，则兼具了对数插值的高亮度优势和Hibbard 算法的低色差优势，副作用较小。另外，Hibbard 算法在插值时是选取梯度最小的方向进行插值，因而可以避免很多双线性算法容易产生的拉链效应。但是同时也会产生很多额外的噪点，主要是因为单方向的插值不能避开单像素长度的梯度。如果另一个方向的梯度也较大，此时算法就无法分辨，容易绕过边缘插值，从而形成噪点。

4 结语

本文基于Hibbard算法，提出了一种利用对数平均强化亮度的改进型插值算法，对暗色图片的还原效果有所改善。实验结果表明：本算法可以有效提高图片在细节处的还原亮度。然而本算法在颜色比例的还原上依然沿用Hibbard 算法的思路，以绿色为基准色，在单方向上进行插值，因而并不能改善Hibbard算法固有的色差问题。同时本算法对图片高亮度部分的改善效果不明显，不能提高还原结果的清晰度。另外，本算法在恢复的过程中进行了两次插值，分别恢复了亮度和颜色比例，计算开销较大。进一步改进的方向具体有：（1）分析三通道梯度值的大小，选取不同的基准色进行插值，以减小色差；（2）采用更高效的亮度恢复算法，减小计算量。然而算法总是优劣并存，任何算法都既有适用场合，也存在固有缺陷。只要针对不同的场景，合理地选择适用的算法，就可以扬长避短，将恢复效果最优化。