液氧涡轮泵阻尼密封设计与动力学特性研究

2023-10-24靳志鸿胡锦华李志刚李军

西安交通大学学报 2023年9期

靳志鸿,胡锦华,李志刚,李军

(1. 西安交通大学能源与动力工程学院,710049,西安; 2. 西安航天动力研究所,710100,西安)

作为液体火箭发动机核心部件之一,涡轮泵主要用于推进剂的输送及增压[1-2], 其关键增压部件离心叶轮处的前、后凸肩泄漏通道面临着极高的进出口压差、转速以及旋流速度,这对叶轮凸肩密封的高效设计和转子抑振是重大挑战。随着我国大推力补燃循环火箭发动机的研制以及发动机性能提升的迫切需求,液体火箭运载能力不断发展,其涡轮泵向着高压比、高转速和高效率的方向发展。随着液体火箭发动机转速和压力的不断提高,密封流体激振成为影响涡轮泵转子稳定运行的主要因素之一。在小间隙动密封环境中,高速转动离心轮前后动静间隙泄漏量控制和涡轮泵转子振动抑制是发展大功率液体火箭发动机需要解决的问题之一[3-6]。

通常涡轮泵的水力设计是针对火箭发动机在额定运行工况下进行的,此时的氧泵效率达到最高。在载人航天登月、火星探测工程中,为保证宇航员和探测器的安全,实现着陆器在月球和火星表面软着陆,发动机需具备10%～100% 深度变推力调节能力。在重复可回收火箭研制中,垂直起降的航天运载器在返回过程中,由于推进剂剩余量逐渐减少,运载器质量越来越小,需要发动机具备大范围推力调节能力,才能实现减速或地面软着陆[7-8]。大范围深度变推力对发动机涡轮泵等工作适应能力提出了很高要求。氧涡轮泵作为发动机的核心组件,叶轮凸肩密封的变工况动力学适应性会直接影响到涡轮泵工作的安全性和可靠性。在发动机变推力过程中,涡轮泵凸肩密封的密封性能随转速、压力和旋流速度而改变,对涡轮泵的整体安全运行有着不可忽视的影响。因此,对涡轮泵凸肩密封在深度变推力工况下的密封性能研究是一个关键问题。

Childs等研究发现,级间密封气流激振力引起了美国航天飞机主发动机高压液氧泵中亚同步振动失稳,采用蜂窝阻尼密封代替传统迷宫密封显著减小了涡轮泵转子亚同步振动,但无法消除;最终通过在蜂窝阻尼密封上游安装防旋板,成功解决了转子亚同步问题[9-10]。Childs和Vance等多年的研究表明,动密封内动压效应诱发的气流激振力对轴系稳定性的影响与密封气流激振动力特性有关,传统的迷宫密封产生的气流激振力可能诱发转子系统失稳,而阻尼动密封可以抑制转子振动(如蜂窝/孔型阻尼密封和袋型阻尼密封)[11-12]。靳志鸿等针对涡轮泵凸肩密封提出了一种新型螺旋阻尼密封,并验证了该新型阻尼密封优于传统迷宫密封的封严性能和对周向旋流的抑制效果[13]。为改善密封对轴系稳定的影响,除了通过增大动静间隙、安装进口止旋装置改善密封来流条件等措施外,研发和应用先进阻尼轴承和阻尼密封结构也是高效抑振的重要手段[14-16]。

孔型密封是一种典型的阻尼密封形式,其原理是,利用流体在泄漏通道内流入圆形孔腔中产生剧烈的涡流以及壁面摩擦作用来耗散高速泄漏工质的动能,从而降低压差两端的泄漏量。尽管原理上与迷宫密封相似,但由于其周向间隔布置的孔腔结构阻断了周向旋流的流动,可以有效降低交叉刚度,改善转子动力特性,并且封严性能也优于传统迷宫密封。方志等数值研究了孔深、孔径对孔型密封泄漏特性的影响,结果发现,深径比(孔深与孔径之比)是影响孔型密封泄漏量的关键参数,气体孔型密封,最佳深径比为0.15～0.25;液体孔型密封最佳深径比为0.5～0.6,该研究对气、液工质孔型密封的结构设计提供了可靠参考[17-18]。Jolly等实验测量了不同转速下水工质孔型阻尼密封的泄漏特性和转子动力特性,并与光滑密封进行了比较,结果表明,相比于光滑面密封,孔型阻尼密封具有优良的封严性能和转子稳定性[19]。

目前,国内外学者对于孔型阻尼密封在液氧涡轮泵中的应用研究较少。赵经明研究了孔型密封在某个实际工况下的泄漏特性和同步振动频率下的转子动力特性,验证了孔腔结构相比无孔腔间隙密封可以降低泄漏量并提高转子稳定性[6]。毛凯等针对某型液氧涡轮泵的前、后凸肩密封不同密封方案的研究表明,相比于原始迷宫密封方案,优化设计的孔型/蜂窝阻尼密封使液氧涡轮泵离心轮前、后凸肩动密封泄漏量分别减小了约19%和21%[19]。李志刚等研究了液氢涡轮泵中孔型阻尼密封的设计准则与密封性能,得出了孔径和孔深对液氢孔型阻尼密封泄漏特性和频率相关的转子动力特性系数的影响规律[20-21]。然而,对于大密度、高黏性的液氧工质,在液氧涡轮泵实际深度变工况下的孔型阻尼密封的泄漏特性、宽频域下的转子动力特性及适应性研究还需要深入探索。

本文针对某型液氧涡轮泵叶轮前凸肩动密封,开展了迷宫密封、蜂窝和孔型阻尼密封的方案设计、性能比较以及深度变推力下的动力学适应性研究。采用“虚拟旁路边界”数值计算模型,同时模拟密封进口的压力场和速度场。在6种发动机变推力负荷(10%～100%)、高进口预旋(预旋比为0.77)条件下,计算了前凸肩孔型阻尼密封的泄漏量和转子动力特性系数,分析了在发动机10%～100%深度变推力工况下的密封性能和转子动力学适应性。

1 液氧阻尼密封方案设计

图1给出了某型液氧涡轮泵离心轮前凸肩密封方案的几何结构(迷宫密封),表1给出了前凸肩密封的具体几何参数和装配尺寸。

表1 前凸肩密封几何尺寸

图1 液氧涡轮泵离心轮凸肩密封结构Fig.1 Shoulder seal for liquid oxygen turbopump centrifugal wheel

保持密封间隙和密封长度的几何尺寸不变,设计了迷宫密封、蜂窝和孔型阻尼密封3种密封方案,其中蜂窝和孔型阻尼密封的方案设计依据文献[19]提供的优化结果。图2给出了某型液氧涡轮泵叶轮前凸肩密封的三维结构示意图,密封流道由密封间隙和静子面迷宫腔、蜂窝孔或孔腔构成。最优的孔型/蜂窝阻尼密封方案的结构尺寸为:孔径D=1.4 mm、孔深H=0.7 mm,周向孔数为128(周期弧度为5.625°)。蜂窝密封的设计准则与孔型阻尼密封相同,因此几何参数与孔型阻尼密封保持一致。

图2 前凸肩(孔型)密封结构示意图 Fig.2 The structure diagram of front shoulder hole-pattern damper seal

表2给出了3种动密封方案详细的齿、孔几何参数和密封尺寸。图3、图4分别给出了迷宫密封和(孔型)阻尼密封的几何结构,包括密封静子件上迷宫齿槽的尺寸参数和孔腔展开示意图,其中N为迷宫齿数。常见孔型阻尼密封的孔腔采用了轴向顺序排列、周向错序排列的排布方式。蜂窝密封的蜂窝芯格几何尺寸和排布与孔型密封一致。

表2 3种动密封几何参数

图3 迷宫密封几何结构Fig.3 The structure diagram of labyrinth seal

图4 (孔型)阻尼密封几何结构Fig.4 The structure diagram of damper seal (hole-pattern)

2 数值方法

2.1 计算模型与网格

根据第1节3种密封设计方案,图5、图6分别给出了前凸肩迷宫密封和(孔型)阻尼密封的三维360°整周计算模型和计算网格。由于液体工质密度大,密封进口的周向速度分量对密封进口的总压和静压分布影响显著,文献[22-23](气体工质密封)通过进口压力边界给定气流角来确定进口预旋速度的方法,不能准确设定密封进口的静压和周向旋流速度。本文通过在密封进口延伸段增设“虚拟旁路”的方法,提出具有“虚拟旁路边界”的动密封计算模型,可以分别准确模拟密封进口位置的高速周向旋流(进口)和高静压力(旁路)边界条件,从而实现密封进口的压力场和速度场双边界条件的准确设定。“虚拟旁路边界”数值模型已经过多次验证,具体可见参考文献[13,28]。

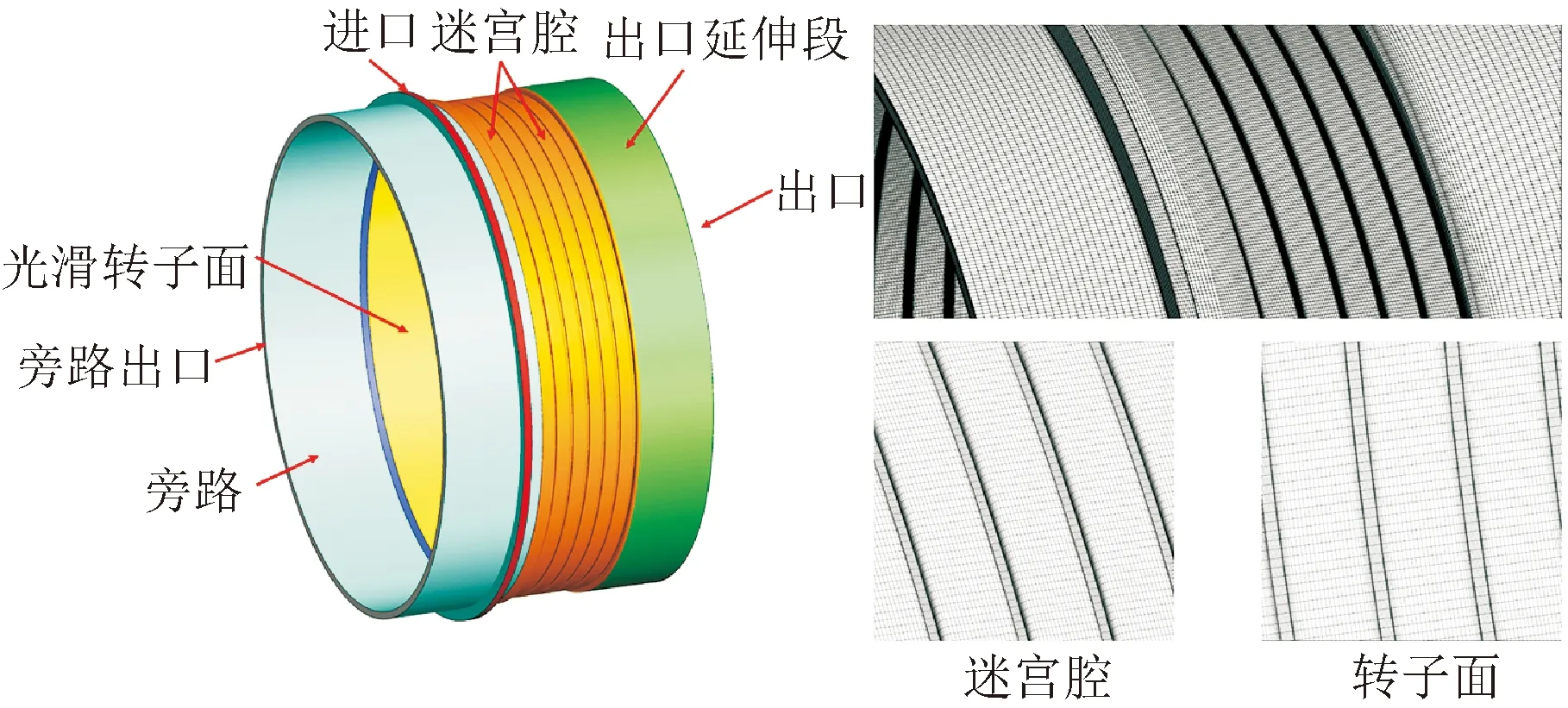
图5 迷宫密封计算模型和网格Fig.5 The numerical model and meshes of labyrinth seal

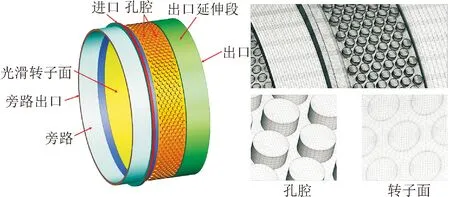
图6 (孔型)阻尼密封计算模型和网格 Fig.6 The numerical model and meshes of damper seal (hole-pattern)

本文采用三维造型软件UG进行密封流体计算域几何建模,基于商业软件ANSYS ICEM对计算域进行结构化网格划分。由于在密封动力特性计算时,需要利用网格变形技术在转子面上模拟转子特定轨迹下的涡动,导致整个流体计算域和计算网格产生非定常变化,因此必须采用全三维的360°整周计算模型。考虑到蜂窝和孔型密封周向错排具有周向旋转周期性,可以对单个周期的计算域进行网格划分后,通过旋转复制获得360°整周的计算网格,大幅减少网格划分难度。以图4中孔型阻尼密封结构为例,每两排孔为一个周期,因此周期性模型的周向周期角度为5.625°。采用“O”形网格对迷宫、蜂窝和孔型腔室进行结构化网格划分和边界层加密,能够获得高质量的网格和近壁面边界层。经网格无关性验证,后续数值计算中迷宫密封、蜂窝和孔型阻尼密封模型的网格节点总数最终设置为8.48×106、1.01×107、1.05×107个,其中密封间隙内设有12个节点以满足微小间隙内剧烈湍流的捕捉。最终主体计算域网格y+值在300以内,满足湍流模型计算要求。

2.2 数值预测方法

基于商业软件ANSYS CFX,本文采用转子无涡动的定常数值方法和转子多频涡动的非定常数值方法,分别获得3种动密封方案的稳态泄漏量和小位移涡动下的动力特性系数,分析额定推力下的密封性能,并进一步评估阻尼密封在深度变推力负荷下的动力学适应性,详细的数值方法见表3。定常计算时,对于光滑转子面的3种动密封,通过对转子面设置壁面转速模拟转子的旋转,所有壁面均无位移;非定常计算时,基于网格变形的动网格方法和多频转子涡动模型,对转子面施加随时间变化的涡动位移和自转旋转速度。文献[24-27]对转子多频涡动模型的参数选取方法和基于网格变形的动网格方法进行了详细介绍。

表3 动密封泄漏量与动力特性数值预测方法

表4给出了某型液氧涡轮泵在6种真实深度变推力负荷(10%～100%)下的前凸肩密封压力、预旋和转速工况参数,在无止旋措施情况下,所有工况的进口旋流比(密封进口旋流速度与转子面线速度的比值)约为0.77。

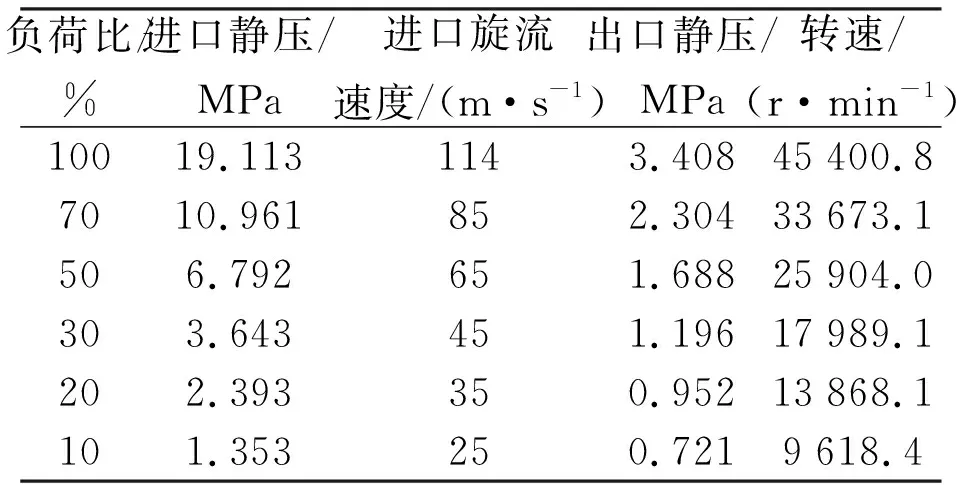
表4 前凸肩密封变工况边界条件

图7给出了本文非定常数值方法中的转子椭圆单频涡动模型示意图。假设转子在绕自旋中心C自转的同时,转子中心绕着无涡动位置O(即静子中心)以某个频率角速度的椭圆轨迹发生以X方向或Y方向为长轴的单频涡动。当多个单频率角速度位移叠加则为多频椭圆涡动,其中转子多频涡动在X、Y方向的叠加位移可以表示为

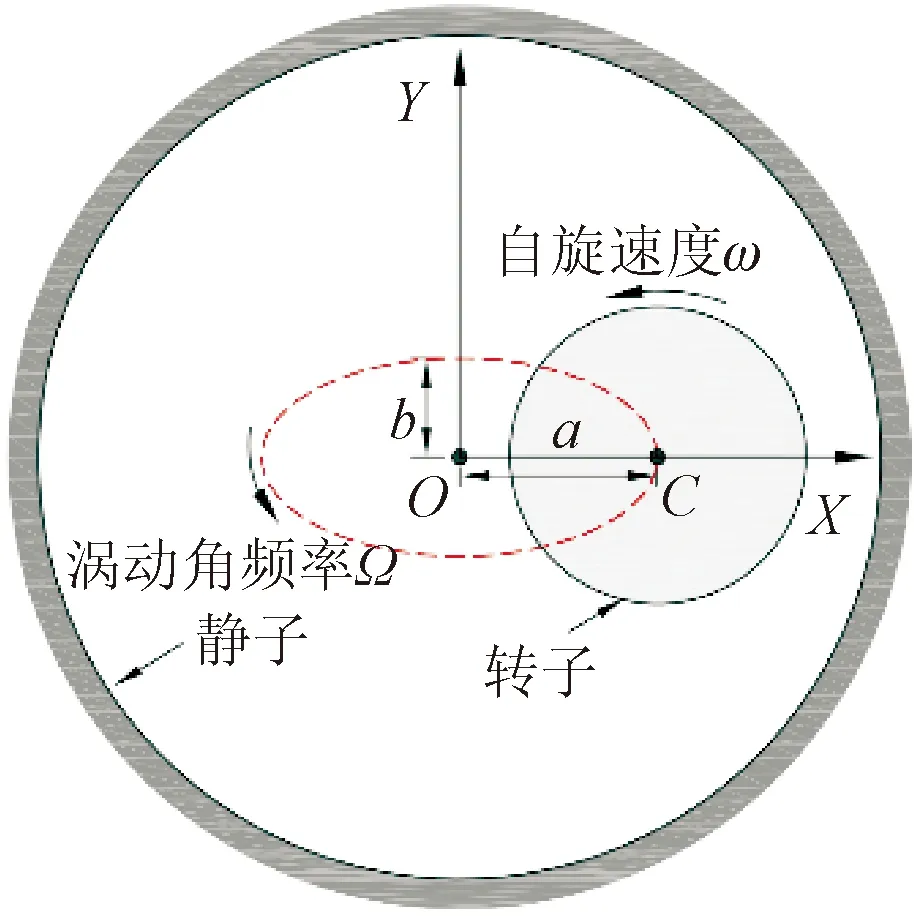
(a)X方向激励

(1)

式中:a、b分别为X、Y方向上每个频率下的涡动位移幅值;N为涡动频率个数;Ωi=2πfi=i2πf0为每个频率对应的涡动角频率,f0为选取的基频。

表5给出了非定常数值方法中6个变推力运行工况点的转子多频椭圆涡动模型参数,位移幅值取a=0.01S,b=0.005S,S为密封间隙。由于深度变推力下的叶轮转速变化范围较大,转子同步振动频率在160.31～756.68 Hz之间。对于低推力负荷的低转速工况,其在远高于同步振动频率时的转子动力特性系数求解会产生失真,不具有频率相关性。本文关注的是更容易引起转子失稳的同步振动频率及次同步振动频率下的密封转子动力特性,因此本文针对不同转速工况点采用了不同的涡动参数,从而更准确、有效地求解目标频域下的转子动力特性系数。

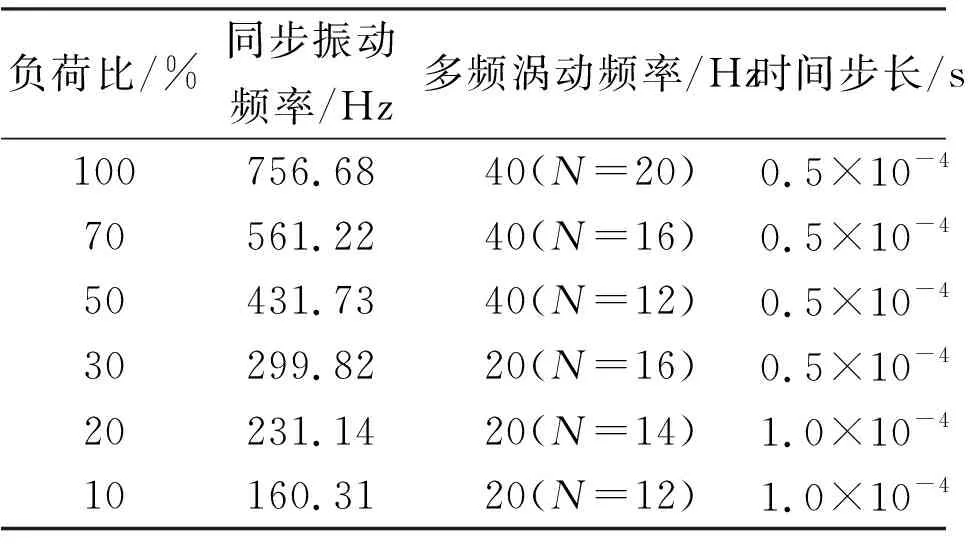
表5 变工况下转子多频椭圆涡动参数

根据转子小位移涡动理论求解力-位移方程,对于液体动密封,由于液体密度较大,因此不可忽略虚拟质量项。若假设密封转子涡动轨迹为圆形,涡动角频率为Ω,圆形轨道幅值为e,则作用在密封定子上的流体响应力可分解为径向力Fr和周向力Ft,力与位移的比值可表示为关于涡动角频率Ω的二次函数,各项系数可通过最小二乘法拟合求解,文献[27-28]给出了具体拟合求解方法

-Fr/e=-Ω2M+Ωc+K=Re(Hxx)+Im(Hxy)

(2)

-Ft/e=Ω2m+ΩC-k=-Re(Hxy)+Im(Hxx)

(3)

式中:径向力Fr是阻止转子径向偏心的中心恢复力;Keff为有效刚度系数;周向力Ft是抑制转子周向进动,表征密封稳定性能力;Ceff为有效阻尼系数;K、C和M分别为密封的直接刚度、直接阻尼系数和直接虚拟质量;k、c和m分别为密封的交叉刚度、交叉阻尼系数和交叉虚拟质量;Hxx、Hxy为x方向的直接阻抗系数和交叉阻抗系数。有效刚度和有效阻尼为

Keff=-Fr/e=Re(Hxx)+Im(Hxy)

(4)

Ceff=(-Ft/e)/Ω=(-Re(Hxy)+Im(Hxx))/Ω

(5)

3 数值方法验证

本文利用Jolly等的孔型阻尼密封实验数据[21],以水为工质,验证了本文动密封泄漏量和转子动力系数的数值预测方法准确性。由于液氧和水具有相近的密度和较强的不可压缩性,液氧涡轮泵常采用水压实验验证泵的水力性能,因此用水工质孔型密封实验数据验证液氧孔型密封的数值方法是可行的。为了保证验证的可靠性,数值验证的孔型密封计算模型几何参数和运行条件与实验数据完全一致。

图8给出了孔型密封泄漏量随转速变化的数值预测结果与实验结果对比。结果表明,孔型密封的数值预测结果相对误差小于9%,变化趋势与实验结果完全吻合,全工况条件下都能获得较好的泄漏量预测结果。因此,本文的CFD稳态泄漏量数值预测方法对液体孔型密封封严性能具有可靠的预测精度。

图8 孔型密封泄漏量预测值和实验值随转速变化曲线Fig.8 Predicted leakage and experimental results versus rotational speed for hole-pattern seal

图9给出了非定常数值方法预测的孔型密封转子动力系数与实验结果的对比曲线,表明预测结果与实验结果吻合良好,趋势一致。因此,目前基于瞬态CFD的摄动求解方法对液体孔型密封的转子动力系数预测是可靠的。

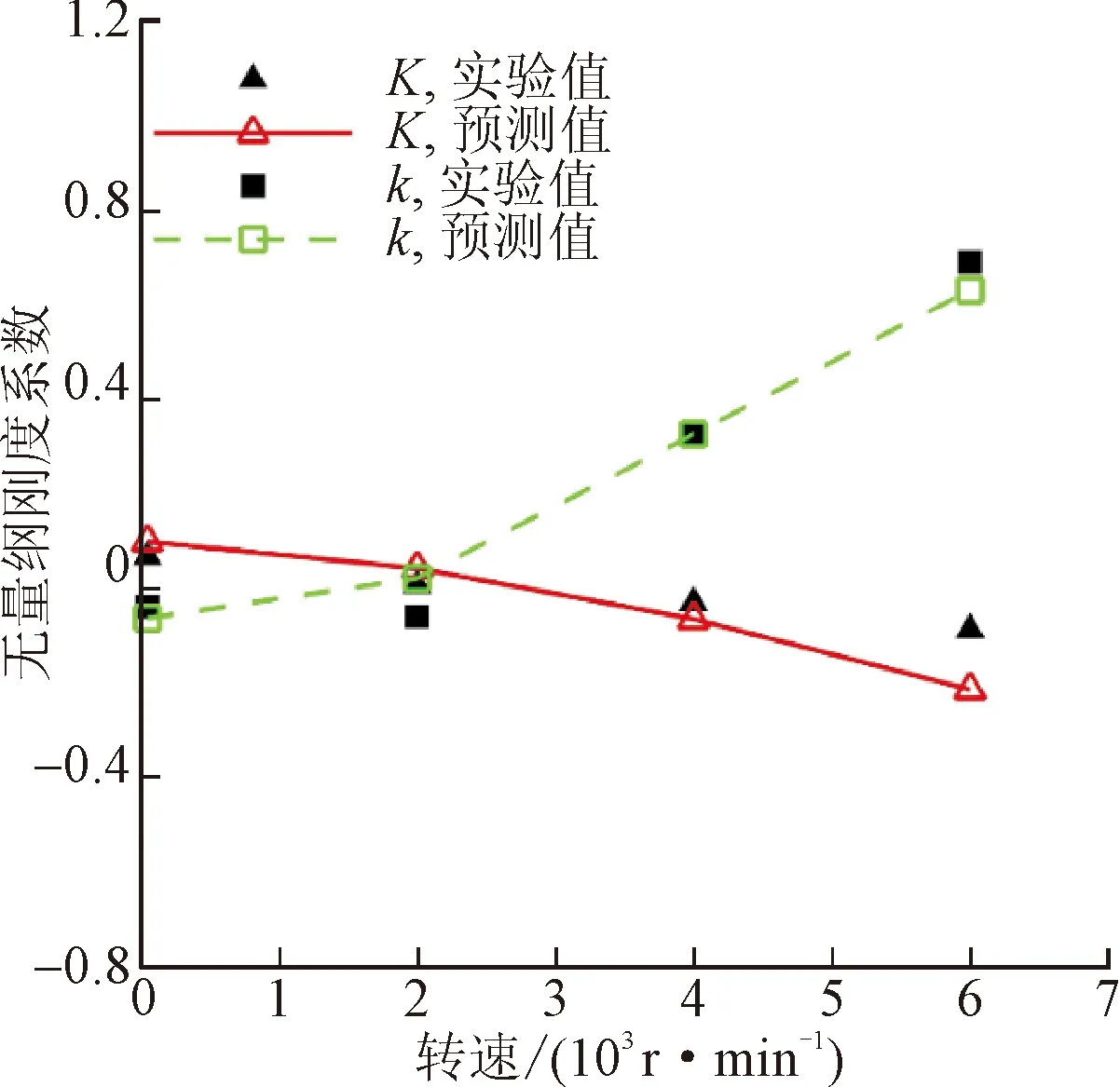
(a)无量纲刚度系数

4 结果与讨论

4.1 动密封方案比较

泄漏特性上,迷宫密封在额定工况下的泄漏量为1.477 kg/s,而蜂窝和孔型阻尼密封由于芯格尺寸和排布相近,泄漏量相差不大,分别为1.212 kg/s和1.218 kg/s。在额定工况下,相比迷宫密封方案,叶轮前凸肩蜂窝和孔型阻尼密封的泄漏量分别降低了17.9%和17.5%。

表6和表7分别给出了某型液氧涡轮泵额定工况下3种前凸肩密封随频率变化的有效刚度和有效阻尼。图10和图11分别给出了3种密封方案有效刚度和有效阻尼随频率的变化曲线。由图可见,迷宫密封的有效刚度随着向高频段发展明显降低,有效刚度为较小的正值,而蜂窝和孔型阻尼密封在向高频段发展时是增大趋势,在高频段处变化不明显,为一个较大的正值,且整体由大到小依次为孔型密封、蜂窝密封、迷宫密封。

表6 3种密封方案的有效刚度

表7 3种密封方案的有效阻尼

图10 3种密封的有效刚度随频率变化曲线Fig.10 Effective stiffness versus frequency for three seals

图11 3种密封的有效阻尼随频率变化曲线Fig.11 Effective damping versus frequency for three seals

蜂窝和孔型阻尼密封的有效阻尼曲线在低频区域极为接近,在高频区域蜂窝阻尼密封的有效阻尼要高于孔型阻尼密封。蜂窝和孔型阻尼密封在由负阻尼向正阻尼变化的穿越频率fco分别为287 Hz和275 Hz,均远低于迷宫密封的661 Hz,能够提供较大的正阻尼抑振频率区间。蜂窝和孔型阻尼密封方案的有效阻尼在全频域下较迷宫密封均有明显增大(同步频率下有效阻尼分别增大了180%和87%),有利于额定工况下的转子系统长期稳定运行。由此,对于额定运行下的液氧涡轮泵转子系统,两种阻尼密封方案均可为系统提供更大的刚度、阻尼以及更宽的抑振频率区间。

4.2 深度变推力下密封动力学适应性

在额定运行工况下的阻尼密封方案,能够为液氧涡轮泵凸肩密封提供更低的泄漏量和更优的转子动力特性,但并不代表深度变推力工况下的阻尼密封性能能够满足高效、安全运行的要求。为进一步评估涡轮泵叶轮前凸肩阻尼密封方案在火箭变推力过程中的密封性能,针对深度变推力负荷下(10%～100%)液氧涡轮泵叶轮前凸肩孔型阻尼密封,开展泄漏特性和转子动力学适应性研究。

图12给出了前凸肩孔型阻尼密封泄漏量随工况推力负荷的变化曲线。由图可见,随着工况推力的增大,孔型阻尼密封的泄漏量呈线性增大趋势,主要是由于推力增大,密封进出口压差也近似线性增大。孔型阻尼密封主要通过密封间隙内高速射流在孔型腔室内的涡流耗散达到降低流速和泄漏量的效果,泄漏量主要决定于进出口压差的大小。

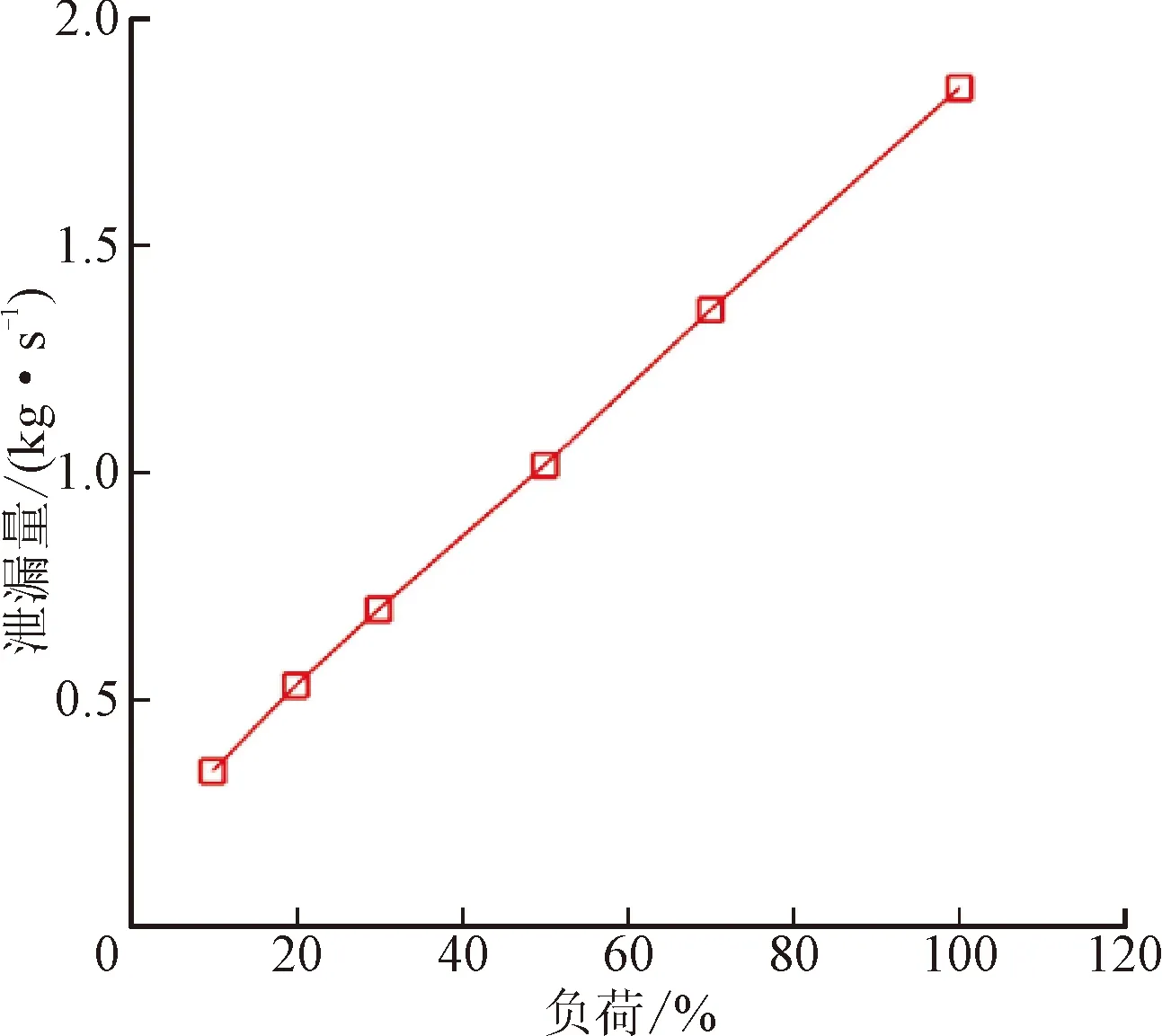
图12 孔型密封泄漏量随工况变化曲线 Fig.12 Leakage rates versus operating conditions for hole-pattern seal

为进一步研究液氧涡轮泵前凸肩孔型阻尼密封的转子动力特性,对6种深度变推力工况下的密封转子动力特性系数进行求解。图13给出了3个与频率无关的转子动力特性系数随工况推力的变化曲线。

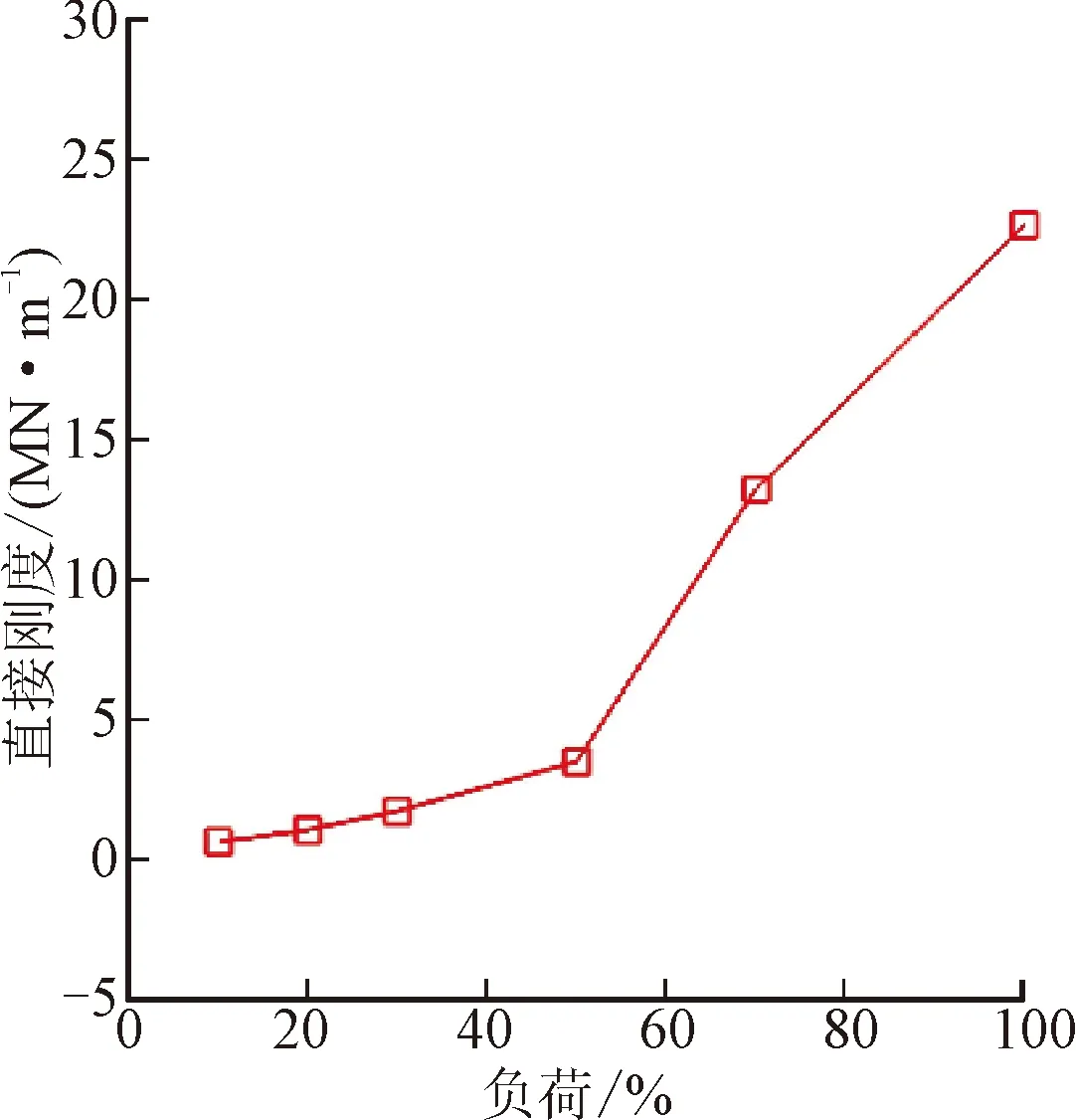
(a)直接刚度

由图13可见,直接刚度、直接阻尼和交叉刚度均随着工况推力的增大而增大,这主要是由于进出口压力、压差和转速显著增大。

图14给出了变工况下孔型阻尼密封的有效刚度随涡动频率的变化曲线,可见,在6种深度变推力工况下,孔型阻尼密封的有效刚度随频率变化不大,接近与频率无关。对于大部分的转子不平衡力,都是与转速同步的,因此同步振动频率下的有效刚度可以直接反映密封的刚度属性。取各工况对应的同步振动频率下的有效刚度,得到图15中同步有效刚度随工况的变化曲线。由图可见,同步涡动频率下的有效刚度随着工况推力的增大而增大,并且在大推力工况下增幅更大。从10%～100%深度变推力负荷过程中,有效刚度值从0.76 MN/m增大到了21.68 MN/m,增大了28.5倍。密封的刚度系数决定了发生振动时的振动幅值,同时与转子系统的固有频率和振动模态有关,这会直接影响到整体的转子动力学性能。若过大的刚度系数达到与系统相当的数量级,这种影响可能被放大并直接影响到转子设计工况下的稳定性表现,因此要在设计阶段进行综合考虑。

图14 深度变工况下孔型密封有效刚度随频率变化曲线Fig.14 Effective stiffness versus frequency for hole-pattern seal under variable conditions

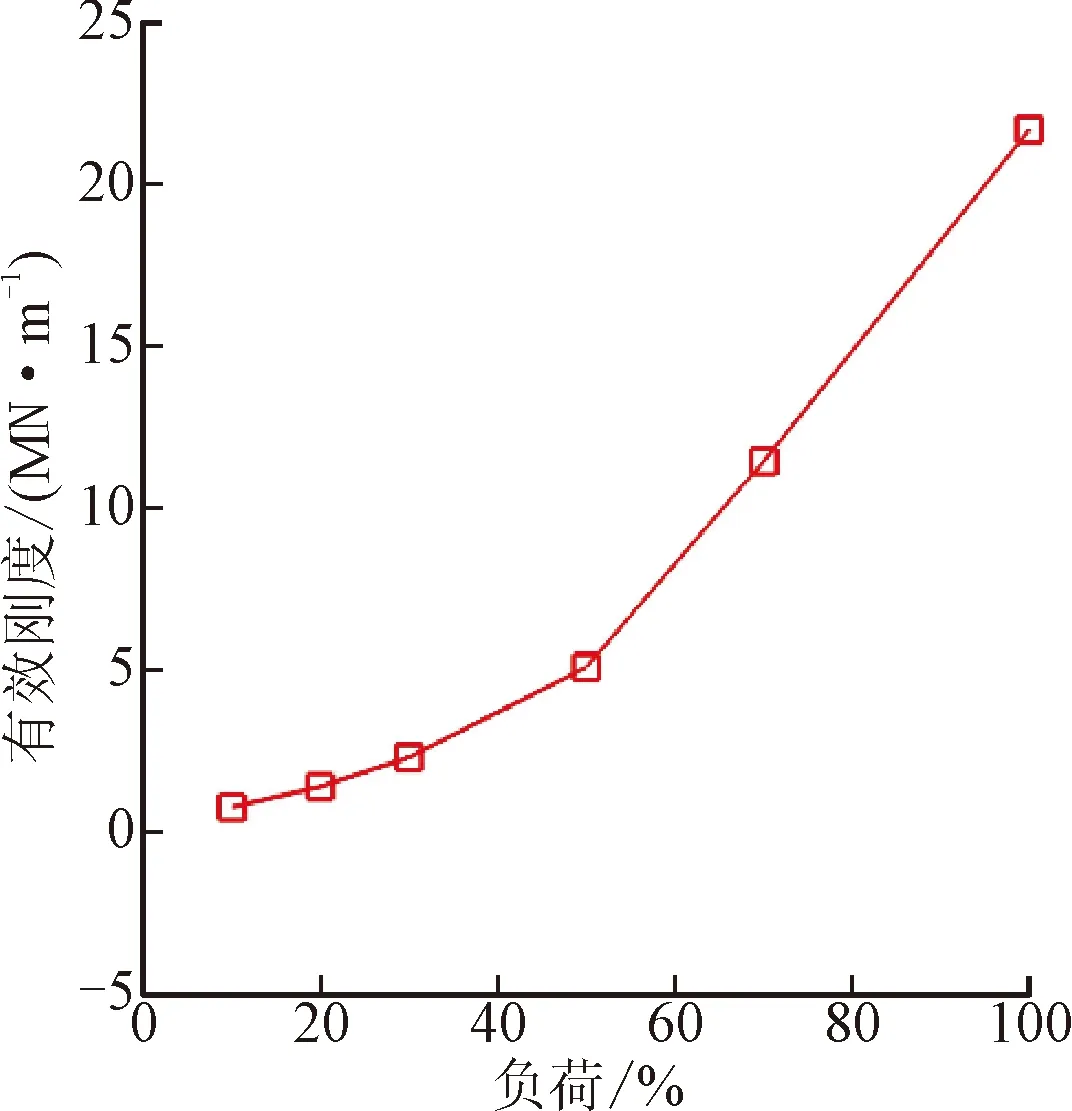
图15 同步振动频率下的有效刚度随工况变化曲线Fig.15 Synchronous effective stiffness versus operating conditions

图16给出了变推力工况下孔型阻尼密封的有效阻尼随涡动频率的变化曲线,可见,随着涡动频率增大,有效阻尼也增大。有效阻尼在高频区为正值且对转子转速的变化不敏感,在低频区为负值且随工况推力增大而显著降低。这主要是由于密封进出口压差增大,尤其是进口压力显著增大,导致转子涡动诱发的流体激振力显著增大。在深度变推力过程中,同步频率下的有效阻尼随着推力负荷的增大而增大,从0.63 kN·s/m增大到2.97 kN·s/m,表明在全推力负荷下均具有较大的正有效阻尼。

图16 深度变工况下孔型密封有效阻尼随频率变化曲线Fig.16 Effective damping of hole-pattern seal versus frequency under variable conditions

图17给出了变工况下孔型阻尼密封有效阻尼穿越频率曲线,可见,随着工况推力的增大,有效阻尼由负值向正值转化的穿越频率也增大。在10%～100%深度变推力工况范围内,穿越频率由50 Hz增大到430 Hz。在大推力负荷工况下的穿越频率接近1/2同步振动频率,存在较大的不稳定频率区,不利于转子系统的稳定性。这主要是由于随着工况推力增大,叶轮转速显著提高,密封流道内周向旋流速度也显著提高,产生较大的交叉刚度,易引起大频率范围内的转子失稳。在小推力负荷工况下,穿越频率约为同步涡动频率的1/3,相对于大推力负荷工况具有更大的增稳抑振频率区间,其阻尼性能也较大推力工况好。总体而言,在接近同步振动频率的高频区域,孔型阻尼密封能为液氧涡轮泵凸肩提供较大的有效阻尼,起到抑振增稳的效果。

图17 深度变工况下孔型密封穿越频率Fig.17 Crossover frequency for hole-pattern seal under variable conditions

为进一步分析泄漏流道内周向旋流速度对密封动力特性的影响,图18给出了孔型阻尼密封间隙内周向旋流速度沿轴向位置变化曲线。由图可见,随着推力负荷的增大,间隙内周向旋流速度也增大,这主要是由于转速的增大以及更高的进口预旋速度。但在70%～100%工况下,在密封前半轴段的旋流速度明显远高于后半轴段的间隙内旋流速度,这主要是在高转速工况下极高的进口预旋速度引起的。因此,在设计阶段,可以通过在密封进口增设防旋板等止旋装置降低密封进口旋流速度,可以有效地改善在大推力负荷工况(70%～100%),尤其是稳定运行的额定工况下,靠近密封进口处过高的周向旋流速度引起的转子失稳问题。