基于跨声速膨胀凝结流动的低温氮气均质成核与异质成核

2023-10-24胡文虎孙皖牛璐彭婧蒋卓君潘良明

西安交通大学学报 2023年9期

胡文虎,孙皖,牛璐,彭婧,蒋卓君,潘良明

(1. 重庆大学低品位能源利用技术及系统教育部重点实验室,400044,重庆;2. 重庆大学核工程与核技术系,重庆,400044; 3. 中国空气动力研究与发展中心,621000,四川绵阳)

凝结作为一种常见的基础物理现象广泛存在于自然界以及工程领域,尤其在喷管、透平机、旋流分离器、低温风洞等场景中,因工质气流极快,往往为跨声速流动甚至是超声速流动,更易导致凝结现象的发生。随着高速飞行器的发展,对风洞全尺寸雷诺数试验需求愈发迫切,常规风洞受限于自身种种原因无法继续提升雷诺数,通过液氮喷雾降低风洞内部温度并利用气化后的氮气作为试验介质被认为是现有提高试验雷诺数方法中的最优方法[1-2]。在温度较低的情况下,氮气由于膨胀降温容易引发均质凝结现象,此外,在极限运行总温工况下生成的冰晶为低温氮气提供凝结核心,发生异质成核,会使得凝结现象在相对较高的温度下即可发生。这两种不同成核形式的凝结现象最终均会影响气动特性预测的准确性。

尽管在二十世纪就有了较为完善的凝结成核理论[3-5]和液滴生长理论[6-7],但是在过去很长的一段时间里,有关凝结流动的相关研究大多是基于湿蒸汽[8-12]和天然气[13-15]进行的。受限于氮气分子间势能理论知识的匮乏,针对低温氮气开展相关研究存在不确定性和困难性,目前基于低温氮气凝结开展相关理论研究和实验研究相对较少[16]。Faro、Wegener等[17-19]借助小型超声速风洞进行了有关氮气凝结的实验研究;Willmarth、Bhabhe等[20-23]分别基于不同的测试手段研究了氮气微尺度成核机理或过冷凝特性,但这些研究中凝结温区均在氮气三相点(63.15 K)以下。Sun等[24-26]使用不同的凝结成核模型和液滴生长模型在液氮级温区对拉瓦尔喷管中的自发凝结进行了数值模拟研究,并借助构建的模型完成了氮气自发凝结现象对气动性能试验的影响分析,但未考虑风洞内存在杂质导致异质成核凝结的影响。异质成核方面,针对透平膨胀机以及超声速旋流分离器背景下开展的研究比较多,陈红梅、鞠凤鸣等分别对一维喷管[8]和二维叶栅[9-10]内湿蒸汽的异质成核现象进行了数值研究,对比自发凝结阐明了存在杂质对凝结过程的影响。边江等[13-15]采用经典成核理论和Gyarmathy液滴生长模型建立了天然气均质成核凝结以及异质成核凝结模型,分析了不同变量对异质成核的影响。

综上,目前国内外有关湿蒸汽以及天然气膨胀凝结流动的研究成果斐然。基于风洞中出现的凝结问题,不少学者也针对低温氮气开展了相关研究,但是目前少有液氮级温区下关于杂质组分存在时氮气发生异质成核的凝结流动特性的研究,突出表现在没有一个统一的模型可以描述低温氮气不同成核形式下的膨胀凝结现象。考虑湿蒸汽、天然气膨胀凝结流动和低温氮气膨胀凝结流动过程具有一定程度的相似性,且相关理论体系比较完备,因此本文在湿蒸汽、天然气膨胀凝结流动研究的基础上建立了适用于不同成核形式的低温氮气膨胀凝结模型,在Fluent软件中依托拉法尔喷管进行了数值模拟,分析了入口温度以及异质核心数和半径对凝结流动的影响,为研究低温风洞内存在杂质致使不同成核形式的凝结流动影响提供了理论依据。

1 数学模型

1.1 控制方程

基于Fluent软件,构建了低温氮气膨胀凝结两相流动模型。考虑氮气在高速膨胀工况下形成的液滴尺度通常是微米量级,质量非常小,形成的液滴随着气相流动在极短的时间内就可以达到气相的速度,因此可近似认为气液两相间无速度滑移。气液两相控制方程分别为

(1)

(2)

(3)

(4)

(5)

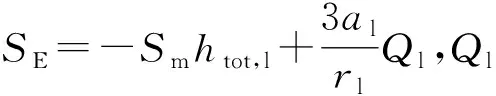
为了使方程组封闭还需添加液滴数守恒方程、湿度连续性方程以及液滴半径液滴数和相关湿度之间的关系式

(6)

(7)

(8)

(9)

(10)

式中:下标hom、het分别表示均质成核、异质成核;J为成核率,m-3·s-1, 表示单位时间单位体积内生成的液滴数;Y为带液量即液相质量分数;N为核心数密度,kg-1;rini为异质核心半径的初始值,m;若仅考虑均质成核现象时将所有下标为hom、het的变量取值为0。

1.2 相变方程

(11)

(12)

式中:qc为凝结系数,一般为1;ξ为非等温修正系数;σ为表面张力,N·m-1;ms为单个分子质量,kg;kB为玻尔兹曼常数,1.380 648 8×10-23J·K-1;Tg为气相表面温度,K;hfg为汽化潜热,J·kg-1;Prg为气体的普朗特数;γ为比热容比;Kn为克努森数;αth为热适应系数,一般取1;Tl为液相温度,K;r为液滴半径,m。

质量源项可以表示为

Sm=mhom+mhet

(13)

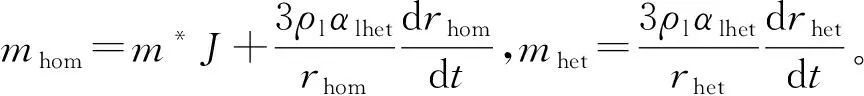
1.3 湍流方程和气体状态方程

RNGk-ε模型在Standardk-ε模型上进行了修正,可以更好地拟合弯曲壁面、流线以及高应变率的流动,但是对于强旋流精度不够。考虑本文数值模拟选用的喷管壁面以及流线的弯曲程度结合计算成本,本文选用RNGk-ε模型。低温风洞通过喷射液氮降低风洞温度,同时利用汽化后氮气作为工作介质进行试验,其气体状态方程采用理想气体状态方程,液相密度、动力黏度、导热率等相关物性参数通过NIST查询、通过UDF模块编程定义并加载到Fluent软件中进行计算。

2 求解计算

2.1 计算域网格划分及模型合理性验证

本文依托拉法尔喷管进行数值模拟,喷管型线采用等膨胀率设计。采用如图1(a)所示二维图形拉伸而来的喷管,在轴向上具有对称性,不同轴向位置截面上流动状况无明显差异,为提高计算效率,可在划分网格时将模型简化为二维。使用二维L型拓扑结构对喷管进行网格划分。喷管结构参数、网格划分后的喷管及边界条件,如图1所示。在进行数值模拟前,进行了网格无关性验证。根据图2最终选用网格数为45 260的网格进行了后续的模拟计算。

(a)喷管结构参数

图2 网格无关性验证Fig.2 Mesh independence

为了验证模型的有效性,模拟再现了计光华[27]进行的一组实验工况。图3对比了实验结果和模拟结果静压沿着喷管流道中心线的变化情况,可见本文所建立的模型预测到了实验中由于凝结相变释放潜热导致流道静压分布出现偏移的情况,由此可以在一定程度上验证模型的有效性。

图3 流道中心线上静压分布的数值结果与实验结果的对比Fig.3 Comparison of static pressure distribution on the centerline of the flow channel between numerical simulation results and experimental results

2.2 数值计算边界条件及工况

入口为压力入口,入口液滴数以及液相体积分数均设置为0;出口为压力出口,进口压力设置为0.4 MPa,进出口压力比为4;壁面设置为无渗流、无滑移、绝热壁面。初场设置为标准初始化,设置初始表压、速度、温度、湍流等参数。

数值计算工况见表1,其中工况1～4用以探究入口温度对均质凝结现象的影响,工况5、6、10、12、13、14用以探究异质核心数密度大小对凝结现象的影响;工况7～11用以探究异质核心半径大小对凝结现象的影响。其中异质核心数及半径参考均质成核凝结现象中自发凝结核心的数值计算得到。

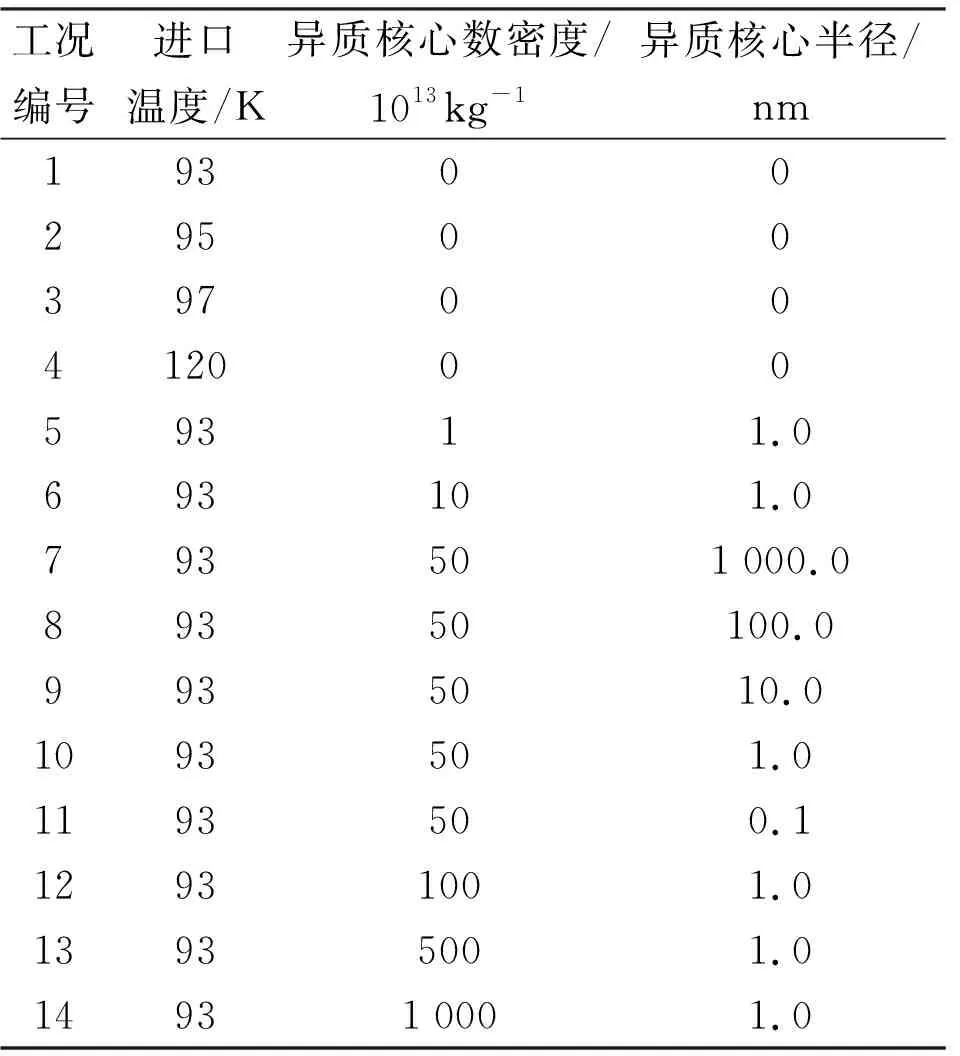
表1 数值计算工况

2.3 Fluent基本求解设定

求解器采用Ansys-Fluent,成核模型、液滴生长模型以及氮气、氮液相关物性参数通过UDF定义,液滴数守恒方程、湿度连续性方程通过UDS定义,湍流模型采用RNGk-ε模型,收敛残差目标设置为1×10-5。

3 均质成核及异质成核模拟结果

3.1 均质成核模拟

从图4均质成核凝结现象发生后喷管内液滴半径沿着流道中心线的变化情况可知,液滴进入生长阶段时半径量级处于10-7m,始终处于μm量级以下,质量非常小。由此可以说明,在建立模型前期假设忽略气液两相间的速度滑移是合理的。

图4 凝结现象发生后液滴半径分布Fig.4 Distribution of droplet radius after condensation phenomenon occurs

选用工况1～4的模拟结果,分析入口温度对均质成核凝结流动的影响。随着非平衡凝结现象的发生,喷管中的流动会产生一定的影响。图5(a)是静压沿着喷管流道中心线的变化对比情况。相比于无凝结现象发生的入口温度为120 K的工况,93、95、97 K 3个工况静压变化具有相似性;发生膨胀凝结现象组的中心轴线静压分布有少许偏移。这是由于非平衡凝结过程考虑了相变中的热力学非平衡过程,在发生凝结的位置,相变产生的潜热加热了氮气流。流道中心线马赫数变化如图5(b)所示,由于潜热的释放,在凝结现象发生过后的喷管下游区域,马赫数的增加也变得稍微缓慢。成核率变化如图5 (c)所示,随着入口温度的降低,最大成核率出现位置前移,凝结现象发生的位置会逐步向喉部靠近,在有限长的喷管内,为液滴生长提供了更多的空间,液滴生长阶段更长,因此出口带液量随着温度的降低有所增加,如图5(d)所示。

(a)静压分布

3.2 异质成核模拟

图6为喷管内氮气膨胀异质成核凝结流动参数分布。氮气进入喷管后随着喷管的收缩,压力、温度逐渐降低,过冷度逐渐增加。与均质成核凝结现象不同的是,当过冷度刚大于0时就发生了异质成核凝结现象,可以观察到异质成核带液量云图中液体质量分数逐渐增加。这是由于异质核心的存在,氮气分子不需要突破自由能障形成凝结核心,而是可以直接簇拥在异质核心上发生凝结现象。随着氮气继续在喷管内膨胀,仍旧发生了均质成核现象,具体情况与前文所分析的仅发生均质成核凝结流动时的现象相同,不同的是由于异质成核凝结现象也会伴随相变释放的潜热,导致过冷度降低。从成核率云图可以看出成核率有所降低,最大成核率从不添加异质核心的1.18×1020m-3·s-1降低到了4.09×1019m-3·s-1,最大凝结核心数也从不添加异质核心的2.887×1015kg-1减小到了1.433×1015kg-1,由此可见异质核心的添加会对均质成核现象产生一定的抑制作用。

喷管流道中心线上成核率以及凝结核心数的变化如图7(a)、图7(b)所示,可以看出,异质核心数为1.0×1013kg-1时,最大成核率以及最大凝结核心数密度分别为1.177×1020m-3·s-1、2.883 9×1015kg-1,与无异质核心添加时的模拟结果1.18×1020m-3·s-1、2.887×1015kg-1基本相同。喷管流道中心线上基于异质成核产生的带液量的变化如图7(c)所示,可以看出,此时异质成核带液量也基本为0,可以认为基本无异质凝结现象发生。随着异质核心数密度不断增大,均质成核现象被抑制的强度逐渐增大。异质核心数密度增大到1.0×1016kg-1时,成核率以及凝结核心数基本没有增长,喷管流道中心线上基于均质成核产生的带液量的变化如图7(d)所示,此时均质成核带液量基本为0,可以认为均质成核基本被完全抑制。

(a)成核率

当异质核心半径为1.0×10-6m时喷管流道中心线上异质成核带液量的变化如图8(a)所示,可以看出,异质成核带液量基本上为0,可认为在该异质核心半径下喷管内的凝结成核形式主要是均质成核。随着异质核心半径的不断降低异质成核现象愈发明显,均质成核现象在一定程度上被抑制,反映在带液量变化(图8 (a)、图8(b))上是异质成核带液量逐渐增大,均质成核带液量逐渐降低。当异质核心半径达到1.0×10-8m以下时,可以发现随着异质核心半径的降低,液相参数基本上没有变化。考虑发生这种情况的主要原因是因为本次数值模拟的5组工况异质核心数密度均为5×1014kg-1,不足以完全抑制均质成核现象。可以预测,当异质核心数充足时,随着异质核心半径的减小,均质成核现象会被完全抑制。