永磁同步电机新型有效磁链固定时滑模扰动辨识策略

2023-10-24刘思源刘凌靳东松

西安交通大学学报 2023年9期

刘思源,刘凌,靳东松

(1. 西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2. 西安交通大学电气工程学院,710049,西安)

永磁同步电机(PMSM)在体积、效率、功率密度等方面具有优势,因而在机器人和电动汽车等领域得到了广泛应用。PMSM是典型的非线性多变量耦合系统。矢量控制(VC)因其优异的动态性能而被广泛应用于PMSM的控制[1-17]。

在设计PMSM闭环矢量控制系统时,控制器的设计是在假设负载转矩扰动为零时进行的[12],因而当负载发生波动时,控制器往往难以较好地抑制负载转矩波动对电机转速产生的影响。这可能导致电机功角不稳定,造成失步、反转甚至损坏设备。为解决负载转矩波动引起的电机状态不稳定,引入负载转矩观测并进行前馈补偿是一种较为常见的做法[11-14]。文献[11]设计了一种新型变系数指数趋近率并应用到滑模负载观测器设计中,前馈至电流环后提升了电流环的动态性能和稳态精度,但由于引入了sigmoid函数,虽然一定程度上减小了抖振现象,但同时降低了滑模观测器的动态响应性能;文献[12]设计了一种降维负载转矩观测器,但由于引入的补偿项是线性误差,因而动态性能有所欠缺;文献[13]设计了一种基于Kalman滤波器的负载转矩观测器,该观测器可以准确跟踪负载转矩的变化,用观测的转矩形成对参考转矩的前馈补偿,可以大大提高系统转速控制性能;文献[14]设计了一种基于无迹Kalman滤波算法的负载观测器,相较于扩展Kalman滤波,摒弃了对非线性函数进行线性化的做法,对提升观测器动态性能具有优势。

传统的负载观测器或存在参数设计繁琐的问题,或在负载发生突变时观测效果不佳。滑模观测器具有参数设计简单,动态性能好的优点[15-17]。但由于其本身引入了符号函数,因而会引入不期望的抖振现象[11],并且传统的滑模观测器存在的缺陷之一就是仅能保证渐进收敛,这意味着在一个具有明确上界的时间限度内无法实现精确收敛,即收敛速度是难以预测的,而这在观测稳态信号时将进一步恶化其输出信号的稳定性和精确性[16]。为解决上述问题,本文将固定时间滑模理论引入负载观测策略。固定时间滑模理论的核心是逆向设计虚拟控制量,构造Lyapunov稳定性方程,进而给出收敛时间的上界[18-20]。固定时间滑模理论的核心优势在于能够迫使误差变量在一个具有明确上界的时间限度内收敛,因而可以控制误差变量的收敛速度,从而在提高滑模观测器的动态性能的同时减少因符号函数而引起的抖振现象。

传统滑模观测器是在静止两相坐标系下建立电机的反电势模型。本文采用的有效磁链模型将电机模型建立在两相旋转坐标系(d-qframe)下,可使所有交流电机的数学模型将具有相同的动态方程,区别仅在于有效磁链的不同。本文采用的内置式永磁同步电机,其模型仅与定子电阻和q轴电感有关,且q轴电流的动态方程就包含了电机转速信息,进而可以获得负载转矩信息[21-23]。采用该模型可以减少电机动态方程数量以及对电机参数的依赖。为进一步提升观测到的信号精确性和动态响应,本文结合扩展状态观测器(ESO)理论对PMSM有效磁链模型进行状态重构和估计,进而构建PMSM三阶扩展状态观测器动态方程[1-9,23-24]。本文基于扩展状态观测器理论,结合PMSM降阶有效磁链模型设计了一种固定时滑模负载观测器(FTSMLTO);将观测到的扰动进行了前馈补偿,改善了电流环控制器对负载变化的抗扰能力,构成一种固定时滑模负载扰动辨识方法,并进行了稳定性证明。最终通过仿真结果证明了所提出的负载观测器的有效性和优越性。

1 PMSM有效磁链模型

为简化分析,假定磁路不饱和,磁滞与涡流损耗影响不计,则永磁同步电机在两相旋转(d-q)坐标系下的IPMSM定子电压方程如式(1)～(3)所示[21-22]

(1)

电磁转矩方程为

Te=1.5npp[ψf+(Ld-Lq)id]iq

(2)

电机运动方程为

1.5npp[ψf+(Ld-Lq)id]iq-TL

(3)

以上式中:ud、uq分别为电机d、q轴定子电压;id、iq为d、q轴定子电流;Ld、Lq为d、q轴电感;Rs为定子电阻;npp为电机极对数;ωe为电角速度;Js为转动惯量;ψf为转子磁链;Te、TL分别为电机电磁和负载转矩;p为微分算子。

对于表贴式永磁同步电机而言,有效磁链ψactive=ψf,而对于本文所用的电机而言,有效磁链ψactive=ψf+(Ld-Lq)id。

电机运动方程为

(4)

将ψactive=ψf+(Ld-Lq)id代入式(1)得电机有效磁链电压模型为

(5)

将其变换为电流动态方程得

(6)

由上式可知,d轴电流动态方程包含电机角度信息,而q轴电流动态方程包含电机转速信息。

2 固定时滑模负载观测器

2.1 FTSMLTO的设计

由式(6)知,仅需q轴动态方程即可构建电机模型。结合电机运动方程(4),即可构建3阶滑模扩展状态观测器如下

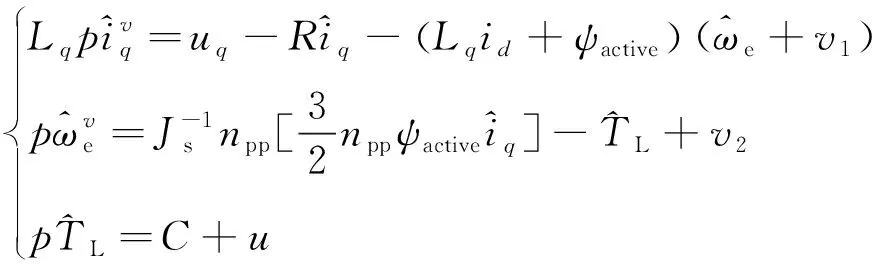
(7)

结合固定时滑模理论,构建虚拟控制率v1为

(8)

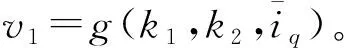
接着引入新的状态变量ε1

τ1pε1=g(1,1,Λ1)

(9)

值得注意的是,在设计观测器参数时,k1、k2应选择的足够大,从而使系统满足半全局终结一致有界性,进而使得系统稳定。

(10)

则

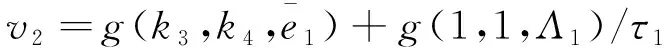
(11)

同理,引入状态变量ε2

τ2pε2=g(1,1,Λ2)

(12)

(13)

则虚拟控制输入为

(14)

式中:τ2是时间常数;ki(i=3,4,…,6)是需要设计的参数。同前文提到的一样,τ2应尽可能小,从而满足收敛的快速性;ki(i=3,4,…,6)应足够大来确保系统稳定。

2.2 FTSMLTO的稳定性证明及收敛时间计算

为进行下一步分析,给出如下引理。

引理1[19]考虑如下微分方程系统

假设存在方程V(x):U→R使得

(1)V(x):U→R是正定的;

(2)存在正实数α,β,任意小的正实数ε,正奇整数m,n,p,q满足m>n,p>q,紧集W0使得pV≤-αVm/n-βVp/q+ε,x0∈W0成立。

引理2[25]对于每个正实数a,b,c和满足1/p+1/q=1的正实数p,q,有如下不等式成立

ab≤cpap/p+c-qbq/q

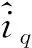
(15)

(16)

(17)

(18)

(19)

构建Lyapunov方程如下

(20)

则式(20)对于时间的导数为

(21)

(22)

根据引理2,可以得到以下不等式(23)

(23a)

(23b)

式中,γi,λi,ηi(i=1,2)均为正实数。同时,存在实数c满足

(24)

将式(15)～(19)、式(22)(23)代入式(21),可得

(25)

得到式(25)后,合理选择参数,使得式(26)成立

(26)

将式(26)代入式(25),则有

(27)

根据式(27)知,合理选择参数使得式(28)成立时系统稳定。

(28)

为求得收敛时间边界,将使不等式(28)成立的条件转换为求解等式(29)

(29)

由于式(29)难以求解,因而将其分解为式(30),求解式(30)即可得到系统收敛时间上界。

(30)

式(30)的解可被写作

(31)

则根据引理1,系统收敛时间上界为

(32)

2.3 观测负载转矩的前馈补偿

为减小负载扰动对于电机控制系统的干扰,进一步提升系统的动态性能,需要将观测得到的负载转矩进行补偿。由于控制系统电气相应速度远大于机械相应速度,因而将观测得到的负载转矩前馈至电流环时,可以提升系统对外界扰动的相应速度,减小负载转矩波动对系统的影响。

结合以上分析,需要将观测得到的负载转矩前馈至q轴电流环进行补偿。因而q轴电流表达式为

(33)

(34)

结合上述分析,构建基于FTSMLTO补偿的PMSM矢量控制系统如图1所示。

图1 基于FTSMLTO补偿的PMSM矢量控制系统框图Fig.1 PMSM vector control block diagram based on FTSMLTO compensation

3 数值仿真分析

为验证算法的有效性,本节对所提出的负载转矩估计算法进行仿真。仿真主要对比了未加负载转矩观测、传统滑模负载转矩观测器[11]及所提出的FTSMLTO的负载转矩观测性能和补偿前后系统抗扰性能变化。仿真所用IPMSM参数如表1所示。

表1 永磁同步电机参数

仿真所用的观测器参数如表2所示。对本文所用IPMSM原型矢量控制系统进行仿真的结果如图2、图3所示。

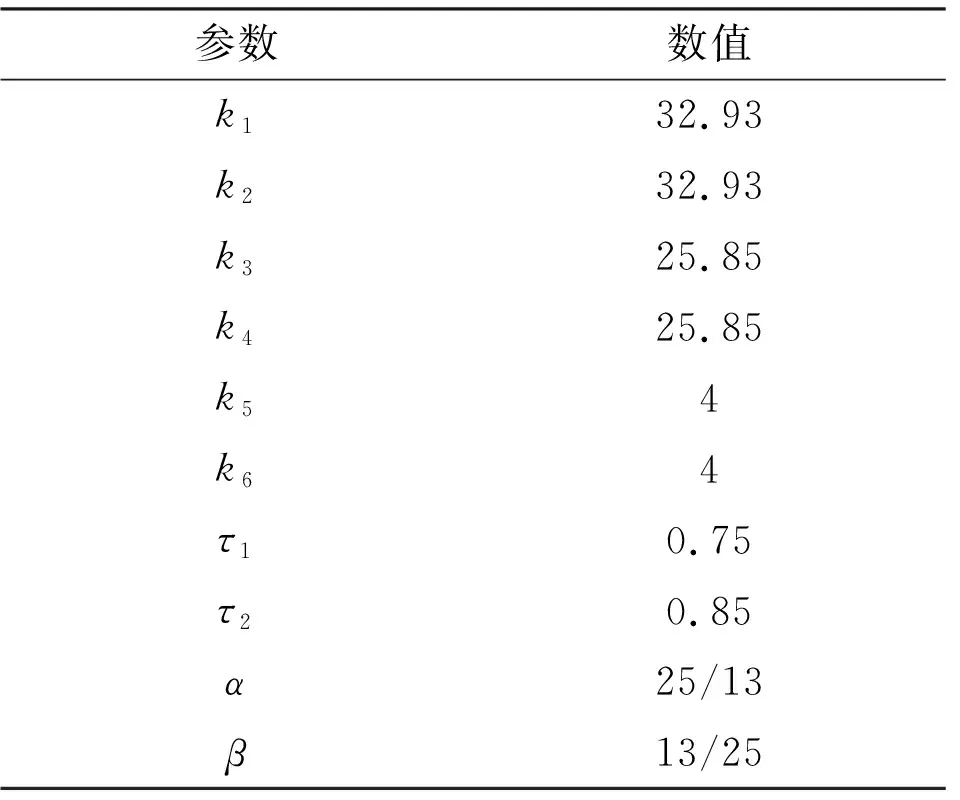
表2 设计的观测器参数

(a)传统滑模负载转矩观测器

(a)未加负载转矩前馈补偿

图2为传统滑模负载观测器及FTSMLTO观测到的负载转矩波形。图2、图3中蓝色线为实际负载转矩,红色线为观测器观测到的负载转矩波形,黄色线为观测器测得的实际转速,绿色线为给定转速。电机在给定转速为1 500 r/min下运行。负载转矩初值由电机转速、转动惯量等决定,在电机转速不变时保持不变。在第0.5 s时负载转矩阶跃增加1 N·m,在2.5 s负载转矩阶跃减小1 N·m;在第2.5 s负载转矩回到初值后再以1 N·m/s的斜率斜坡降低2 s;在第4.5 s时阶跃回到初值,接着以初值为直流偏置,幅值为1,周期为1 s的正弦波运行2 s;在第6.5 s时回到初值。

从图2(a)中可知,在传统负载观测时,稳态时存在较大的稳态误差,最大误差约0.3 N·m;动态时响应较差,形成了锯齿波,难以精确跟踪电机负载转矩。尽管在稳态时传统滑模负载观测器能够观测出负载转矩,但动态时效果很差,这在需要精确补偿电机负载转矩的应用场景下是不可接受的。而采用FTSMLTO后,从图2(b)中可知,稳态误差最大值减小至约0.05 N·m,并且动态响应大大提高,在负载转矩扰动情况复杂时也能精确跟踪,大大提升了负载转矩的观测精度。

图3为将不同负载观测器观测值前馈至电流环后的转速响应。图3(a)为未加负载转矩前馈补偿时的转速波形,此时正向最大超调为112 r/min,负向最大超调-221 r/min,负载转矩为正弦波时超调为±60 r/min;图3(b)为前馈补偿传统滑模负载转矩观测值时的转速波形,此时正向最大超调为110 r/min,负向最大超调-216 r/min,加正弦负载时超调为±58 r/min;图3(c)为前馈补偿FTSMLTO转矩观测值时的转速波形,此时正向最大超调为100 r/min,负向最大超调-188 r/min,加正弦负载时超调为±45 r/min。采用FTSMLTO前馈补偿后相较于未补偿时转速正向最大超调减小约10.7%,最大负向超调减小约14.9%,正弦负载时超调减小约25.0%;相较于传统滑膜负载观测器前馈补偿后转速正向最大超调减小约9.1%,负向最大超调减小约13.0%,正弦负载时超调减小约22.4%。由上述分析得出,FTSMLTO前馈补偿后电机转速动态性能得到了大幅提升。

由图2和图3知,采用FTSMLTO相比传统滑模负载观测器能够大幅提升负载观测值的精确性和动态性能;前馈补偿至电流环后,电机转速动态性能也得到了提升。