翼型下表面柔性襟翼流动控制机理研究

孟俊苗,韩佳坤,陈刚

(1. 长安大学公路学院,710064,西安; 2. 西安交通大学航天航空学院,710049,西安;3. 西安交通大学机械结构强度与振动国家重点实验室,710049,西安; 4. 西安交通大学陕西省先进飞行器服役环境与控制重点实验室,710049,西安)

仿生飞行器的滑翔或长距离飞行要求其自身拥有灵活避障的能力[1]。实际操作上的限制为仿生飞行器的设计带来了许多挑战,其中,低雷诺数(通常为102～103)环境下,仿生翼边界层的流动控制就是一个十分棘手的问题[2-3]。然而,自然界中的鸟类则以灵活性和机动性闻名[4],这得益于漫长的生物进化使其形成了利用柔性羽毛实现流动控制的机制[5]。鸟类翅膀的上下表面均覆盖有羽毛,当其飞行姿态发生突然变化时,附着在鸟类翅膀上下表面的次级羽毛会迅速翘起,这可以使鸟类避免在飞行过程中突然产生失速。受鸟类飞行翅翼的启发,利用仿生襟翼开展流动控制已逐渐成为具有重要发展前景的流动控制技术之一[6]。

然而,仿鸟类羽毛的襟翼却经历了相对漫长的发展过程。早期,Carruthers等[7]将鸟类的次级羽毛视为一种类似于自适应襟翼的增升装置,提出利用襟翼延迟流动分离获得升力的猜想,而Bramesfeld等[8]则通过风洞试验给出了自适应襟翼“压力坝”的作用机制,指出自适应襟翼可以有效阻挡翼型尾缘分离气流向上游的发展,从而使上游压强降低以减少对翼型表面流动分离的影响。随后,一系列的风洞试验[9-10]也证实了自适应襟翼在流动控制中具有抑制流动分离的效果。与此同时,固定的刚性襟翼也被用于研究鸟类羽毛的流动控制机制。Johnston等[11]通过改变刚性襟翼的安装角度,研究了不同攻角下刚性襟翼对翼型气动性能的影响。但与鸟类的柔性羽毛相比,简化的刚性襟翼模型缺少对几何非线性流固耦合效应的分析,不能完全说明次级羽毛流固耦合特性的流动控制机理。Wang等[12]开创性地在翼型上表面安装了真实的羽毛,讨论了羽毛对翼型气动性能的影响。研究证实,柔性襟翼在翼型上表面边界层的变形能够更加有效地抑制流动的分离,进而产生失速延迟的效应。然而,试验研究不仅价格昂贵、可操纵性差,而且很难系统地给出完整的流场信息以全方位地揭示流动分离控制的物理学本质。因此,需要借助数值模拟的手段来完善相关流动控制机理的研究。

面对类似于鸟类柔性羽毛的大变形结构,传统的数值方法很难克服网格畸变的问题。近年来,浸入边界法的发展为处理大变形结构的流固耦合问题提供了新的数值计算策略。Venkataraman等[13]利用该方法对刚性自适应襟翼主动运动下的非定常流动进行了数值模拟研究,进一步证实了襟翼的增升作用。Nirmal等[14]同样利用浸入边界法并结合不可压N-S方程对由铰链连接的多个刚性襟翼的流动控制进行了研究。遗憾的是,这些基于浸入边界法开展的襟翼流动控制研究,均以刚性主动运动的流固耦合特性为主,其结构运动只有一个自由度,这与柔性襟翼利用自身流固耦合特性进行流动控制的机理研究相差甚远。

不仅如此,与鸟类羽毛作用机制相比,当前的研究还局限于利用翼型上表面襟翼进行流动控制,翼型下表面流动控制机理的研究并没有给出。本文建立了一种能够处理柔性结构大变形非定常流动的IB-LB-FEM流固耦合数值模拟框架,并仿照低雷诺数下鸟类次级羽毛的流动控制机制,提出了利用翼型下表面柔性襟翼进行非定常流动控制的方法。重点研究了下表面柔性襟翼位置和刚度系数对翼型非定常流动的影响,进而揭示了下表面柔性襟翼非定常流动控制的机理,以期为解决仿生飞行器的流动分离提供新的研究思路。

1 数值方法及验证

1.1 IB-LB-FEM流固耦合数值方法

采用格子Boltzmann方程(LBE)作为不可压流体的控制方程

gi(x+eiδt,t+δt)-gi(x,t)=

Ωi(x,t)+δtFi(x,t)

(1)

式中:x是流体粒子的空间坐标;t是时间;δt是时间步长;下标i表示流体粒子的运动方向,共m个;gi表示各个方向流体粒子的密度分布函数;ei为流体粒子的离散速度;Ωi为离散碰撞项;Fi为作用在流体粒子上的外力。

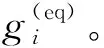
(2)

式中:τ为无量纲松弛时间;wi为离散速度ei对应的权重系数;u为流体的矢量速度;cs表示格子声速;f为作用在液体上的体积力。

对于流场中柔性结构的边界处理,本文采用基于速度修正的浸入边界法(IBM)[18-19]。该方法中流场欧拉点上的修正速度δu可以通过结构拉格朗日点上的修正速度δuL插值获得,即

x∈Π

(3)

作用在流体欧拉点上的体积力f可以根据修正速度δu得到

(4)

式中ρ为液体密度。

因此,通过外力项便建立了一种能够处理复杂动边界非定常流动问题的浸入边界-格子Boltzmann方法(IB-LBM)。考虑到柔性结构流固耦合面临的几何非线性,采用有限元法(FEM)处理结构的动力学方程

(5)

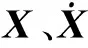
将有限元法中的单元节点视为结构边界的拉格朗日节点,便可以将FEM引入到IB-LBM计算框架。采用Newmark-β方法[21]对结构动力学方程进行求解,则在t+Δt时间步中,结构的动力学方程可以表示为

(6)

通过切线刚度矩阵法[22]可以得到t+Δt时间步中内力Fint,t+Δt的表达式

Fint,t+Δt=Fint,t+KT, tδX

(7)

式中:δX=Xt+Δt-Xt表示位移增量;KT,t是全局坐标系下结构的切线刚度矩阵

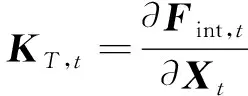
(8)

结构局部坐标系与全局坐标系之间变量的转换可以通过转换矩阵Te进行关联,因此,全局坐标系下结构的切线刚度矩阵可以通过组装局部坐标系下单元刚度矩阵获得,即

(9)

因此,基于浸入边界法(IB)很容易将有限元法(FEM)和格子Boltzmann方法(LB)相结合,从而构建一种通用的IB-FEM-LB流固耦合非定常流动数值模拟方法。

1.2 算法验证

通过模拟一个柔性平板绕流的标准流固耦合试验算例[23],对本文构建的IB-LB-FEM流固耦合数值模拟方法进行验证。

选用与文献[23]中相同尺寸的柔性平板为研究对象,如图1所示。定义流场的雷诺数为

(a)三维平板绕流几何模型

(10)

式中:w为柔性平板的宽度;υ为流体的动力黏度系数;U∞为来流速度。

图2给出了本文数值模拟的计算结果,并与文献[23]中的试验结果进行对比。图中,横坐标x/L表示柔性平板的无量纲水平位移,纵坐标y/L表示柔性平板的无量纲垂直位移。从图2可以看到,本文的计算结果与文献结果吻合良好,证明本文所建立的三维IB-LB-FEM流固耦合数值模拟方法能够满足计算精度的要求。

图2 不同雷诺数下三维柔性平板的挠曲线Fig.2 The deflection curves of three-dimensional flexible plate with different Reynolds numbers

2 问题描述

2.1 柔性襟翼模型

仿照鸟类翅翼次级飞羽的流动控制,本文在标准NACA0012翼型的下表面引入了仿生柔性襟翼,如图3所示。选择NACA0012翼型,是因为其气动外形接近于大型鸟类翅膀的几何形状[5]。鸟类的展弦比相对较大[24],三维效应并不明显。为避免三维效应对翼型表面非定常流动的影响,本文将柔性襟翼进行准三维简化。采用长度为l,宽度为d的平板结构作为柔性襟翼的简化模型。其中,d=0.005c(c为NACA0012翼型的弦长),表示柔性襟翼的厚度,并选用一个格子网格尺寸作为展向长度。

图3 具有下表面柔性襟翼的NACA0012翼型Fig.3 The NACA0012 airfoil with a lower surface flexible flap

本文将重点研究下表面柔性襟翼流固耦合特性对翼型非定常流动分离的影响,因此特定义以下参数。下表面柔性襟翼距离翼型前缘O点的距离p,翼型攻角α=20°。根据已有文献[5],安装角度θ恒为90°。定义柔性襟翼的无量纲长度L=l/c,无量纲位置参数P=p/c,刚度系数K=EI/(ρfU∞2L3),其中,E是柔性襟翼的弹性模量,I为襟翼的截面惯性矩;质量比M=ρsw/ρfL,其中w为襟翼展向长度,ρf表示流体密度,ρs表示襟翼的密度。

2.2 流场参数

流场的计算域如图4所示,沿来流X方向的长度L=15c,垂直于来流方向的高度为H=5c,展向长度w为一个格子网格尺寸0.1c。翼型的前缘O点距离左侧速度入口的距离为2.5c,流场右侧为出口边界,其余边界均采用滑移边界条件。来流速度恒为U∞,因此流场的雷诺数为

图4 流场计算域及网格加密示意图Fig.4 The calculation domain and grid refinement

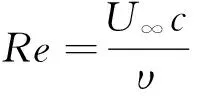
(11)

式中υ为流体的运动黏性系数。为描述低雷诺数下的流动分离,本文雷诺数取500。

采用基于LBM的多域网格加密方法[25]对流场计算域进行局部加密。如图4所示,在距离翼型前缘O点0.5c处,加密区域的大小为l×h=4c×2c,展向长度与整体计算域展向长度相同。加密区域内的流场网格尺寸最小为0.006 25c,最大为0.1c。加密区域的网格数量约为20.5万,计算域整体的网格总数量约为28.2万。其中,网格加密区域的选择和网格划分的原则是在文献[5]的基础上展开的,且本文数值算法的网格收敛性验证已在之前的工作[26]中进行了详细的介绍。翼型和襟翼表面采用基于速度修正的浸入边界法,以满足壁面无滑移的边界条件。

3 结果分析

3.1 柔性襟翼位置对翼型气动特性的影响

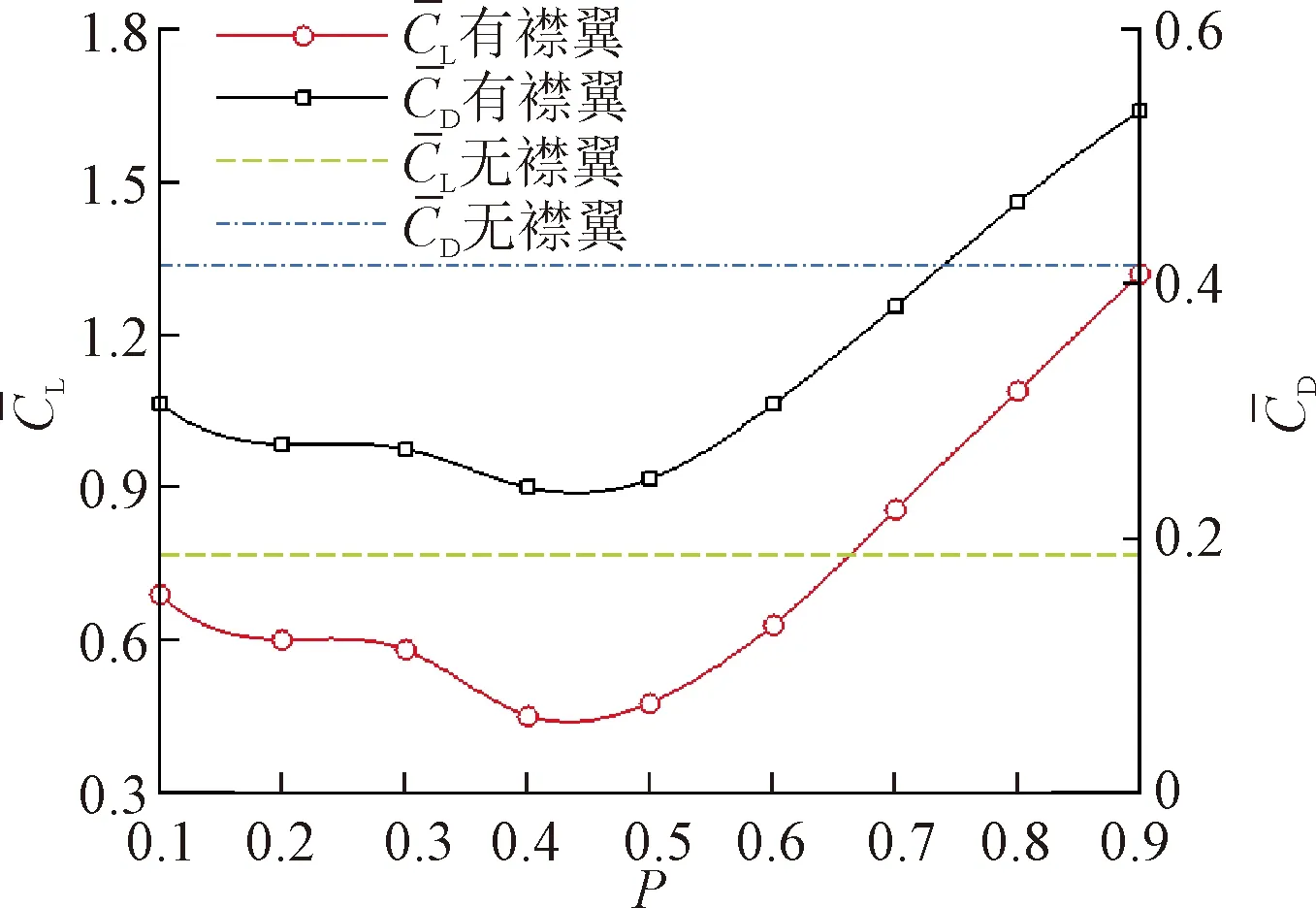
本文提出利用下表面柔性襟翼进行流动控制的方法。图5给出了不同位置的下表面柔性襟翼对翼型升阻力系数的影响。图中,t*表示无量纲时间。柔性襟翼的无量纲长度L=0.1,刚度系数K=0.1,质量比M=10。从图5可以看到,当下表面柔性襟翼位于翼型的前半段(即P≤0.5)时,与无襟翼翼型相比,具有下表面柔性襟翼的翼型其瞬时升力系数CL和瞬时阻力系数CD均减小。然而,当下表面柔性襟翼位于翼型的后半段(即P>0.5)时,具有下表面柔性襟翼的翼型其CL和CD均大于无襟翼翼型的气动结果。可见,随着柔性襟翼向翼型尾缘移动,气动性能逐渐提升。

(a)P=0.3

(a)平均升阻力系数随柔性襟翼位置的变化

3.2 不同位置柔性襟翼的流动控制机理

为建立柔性襟翼流固耦合特性与翼型非定常流动控制的关系,图7给出了同一时刻下柔性襟翼在不同位置时翼型周围的流线分布。从图7中可以发现,当柔性襟翼位于翼型前半段时,其上表面的流动分离几乎保持一致,不同的是,由于下表面柔性襟翼的存在,流体绕过襟翼后在其后方形成了新的逆时针涡,进而影响了翼型的气动特性。具体表现在,P=0.3时,柔性襟翼之后产生了新的流动分离现象,分离再附着点位于翼型的尾缘附近,形成新的逆时针涡并没有影响到翼型尾缘的逆时针后缘涡。因此,相比于无襟翼翼型,柔性襟翼下游的逆时针涡内呈现流速大压力小的特点,从而减小了翼型的瞬时升力。然而,当P=0.5时,柔性襟翼之后流动分离的再附着点刚好位于翼型的尾缘处,此时,瞬时升力减小的原因依旧与襟翼后方的逆时针涡的压力相关。

(a)P=0.3

当柔性襟翼位于翼型下表面的后半段时,襟翼后方形成的逆时针涡开始干扰翼型尾缘的逆时针后缘涡,后缘涡强度增强使得翼型的瞬时阻力开始增加,同样,襟翼后方逆时针涡强度的削弱使得翼型的瞬时升力增加。此外,受到襟翼流动分离的影响,翼型上表面的涡的分布产生了明显不同,尾缘的涡被襟翼后方涡的吸引而快速脱落,从而影响了翼型上表面的流动分离。当P=0.9时,留给柔性襟翼后方逆时针涡的发展空间相对较小,流动分离产生的较小的逆时针涡同样会影响翼型下表面的压力分布,而且增加了翼型尾缘逆时针后缘涡的强度,因此,翼型的升力和阻力均有所增加。

综上,翼型下表面柔性襟翼通过自身的流固耦合特性将会诱导下表面的流动分离,使其靠近翼型尾缘部分的流动分离影响翼型后缘涡的形成,进而改变上表面的非定常流动特性,形成新的流动控制机制。

3.3 柔性襟翼刚度系数对翼型气动特性的影响

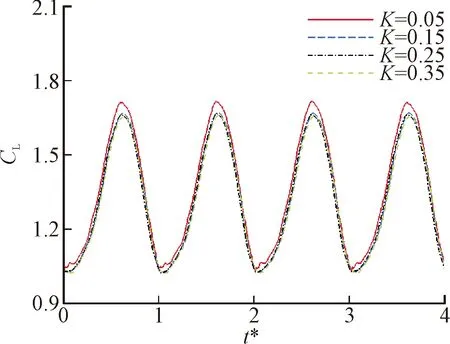
本文研究了下表面柔性襟翼流固耦合特性对低雷诺数下翼型非定常流动控制作用机制。图8给出了不同刚度系数的下表面柔性襟翼对翼型气动力学系数时程曲线的影响,其中,襟翼的L=0.1,P=0.9,M=15。从图8中可以看出:不同刚度系数K下翼型气动力学系数时程曲线的周期特性基本一致,但翼型的瞬时升力系数CL和瞬时阻力系数CD并不相同;柔性襟翼的刚度系数越小,翼型对应的瞬时升力系数CL和瞬时阻力系数CD越大,这表明柔性襟翼的材料属性将明显改变翼型的气动特性。为了衡量柔性襟翼利用流固耦合特性进行流动控制的机制,仍需要给出升阻力系数的平均量化结果。

(a)升力系数时程曲线

(a)平均升阻力系数随刚度系数的变化

3.4 不同刚度系数柔性襟翼的流动控制机理

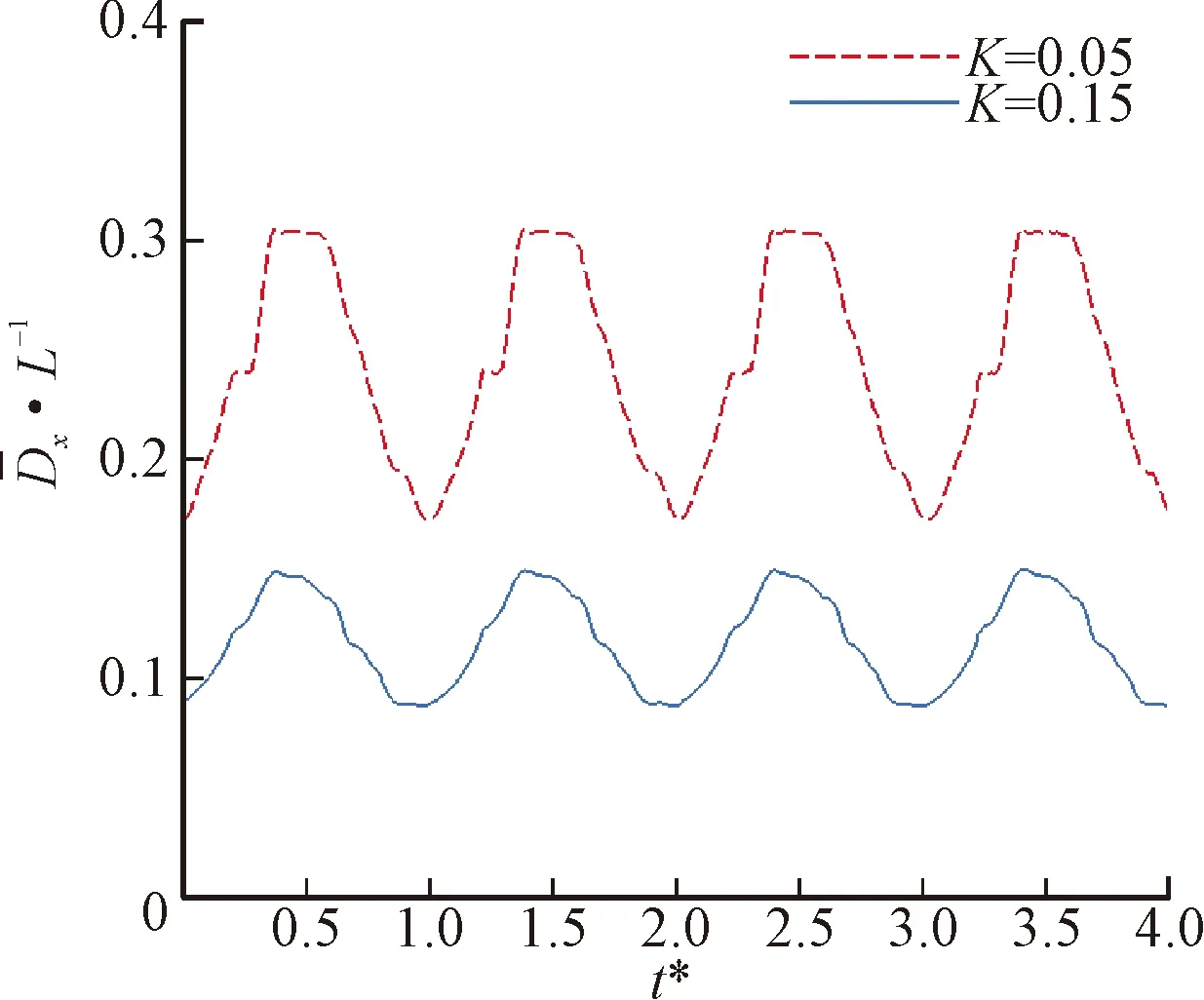
(a)柔性襟翼水平位移随时间的变化

图11给出了同一时刻不同刚度系数的柔性襟翼及翼型周围的流线分布。可以看到,不同刚度系数下翼型上表面的流动分离基本一致。由于下表面柔性襟翼不同刚度系数下其自身的变形不同,在流固耦合作用下襟翼周围的非定常流动发生扰动,同样产生了不同程度的流动分离。在图11(a)中,当K=0.05时,柔性襟翼发生了明显的弯曲变形,当流体绕过襟翼后在其后方迅速形成了饱满的顺时针涡,由于变形导致柔性襟翼末端与翼型下表面的间距相对较小,顺时针涡干扰翼型尾缘的后缘涡,从而增强了后缘涡的强度。随着刚度系数的增加,当K=0.1时,柔性襟翼变形相对较弱,柔性襟翼末端与翼型下表面有足够的空间,翼型尾缘顺时针涡的形状和强度更大,其与尾缘涡的相互干扰使得翼型的瞬时升阻力均明显减小。由此可见,K=0.05时下表面柔性襟翼流固耦合特性下的变形使得襟翼后的顺时针涡能够与翼型上表面的涡快速融合,翼型能够获得更好的气动性能。

(a)K=0.05

尽管下表面柔性襟翼并没有直接影响翼型的流动分离,但却通过对下表面非定常流动的扰动,形成了新的非定常流动分离进而影响了翼型的气动性能。靠近翼型尾缘的下表面柔性襟翼其流固耦合特性会直接影响上表面尾缘涡的发展,进而对翼型的非定常流动分离产生有效的控制。

4 结 论

本文采用面向柔性结构流固耦合特性所建立的非定常流动IB-LB-FEM数值模拟方法,研究了翼型下表面柔性襟翼的流动控制机理,并从气动特性、结构变形、涡的演化等角度系统分析了柔性襟翼对翼型非定常流动分离的控制机制,给出了翼型下表面柔性襟翼位置、刚度系数对翼型非定常流动控制的影响,提出下表面柔性襟翼流动控制的方法,主要结论如下。

(1)与无襟翼翼型相比,下表面柔性襟翼对于翼型整体气动性能的影响相对明显。这是因为下表面柔性襟翼通过扰动翼型下表面的非定常流动,在襟翼后方形成新的流动分离,从而影响了翼型的气动特性。

(2)当下表面柔性襟翼靠近翼型前缘时,前缘襟翼阻挡来流进而在下表面后方形成涡流导致升力与阻力均有所下降。当柔性襟翼位于0.9c处,翼型的平均升阻比较无襟翼提升了33.32%。柔性襟翼的下游形成的分离涡,成为了下表面柔性襟翼流动控制的关键。

(3)通过调整柔性襟翼的刚度系数,可以改变襟翼的变形特性,襟翼后方形成的涡与不同刚度系数柔性襟翼之间的相互作用成为影响翼型整体气动性能的主要因素。

本文的研究结果将为新型仿生飞行器低雷诺数环境下的流动控制提供新的理论支持。