一种基于级数函数的新型拱轴线
2023-10-23谢肖礼杨创捷
邱 辰,谢肖礼,覃 霞,杨创捷
(1.广西大学 土木建筑工程学院,南宁 530004;2.梧州学院 机械与材料工程学院,广西 梧州 543002;3.广西科学院,南宁 530007)
0 引 言
拱圈的线形直接影响拱桥的内力分布与大小[1], 一般认为理想的拱轴线应与拱上各种荷载作用下的三铰拱压力线相吻合, 此时沿拱轴线的每一正截面都无弯矩和剪力, 只承受轴向压力作用, 这样的拱轴线被称为合理拱轴线。
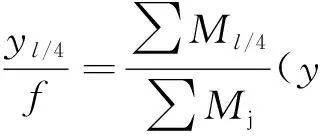

1 新型拱轴线初始方程的建立
1.1 力系等效分析
拱圈受力状态如图1所示, 计算跨径l, 矢高f, 水平推力H, 拱顶弯矩M0, 拱圈自重为沿弧长分布的均布荷载g(x), 吊杆或立柱的集中力为Pi(i=1, 2, …,n), 拱圈所承担的恒载为g(x)与Pi之和。为便于运算, 据圣维南原理将集中力Pi用静力等效均布荷载q(x)代替, 荷载等效对结构的整体受力不产生影响, 仅影响集中力作用点附近的受力。
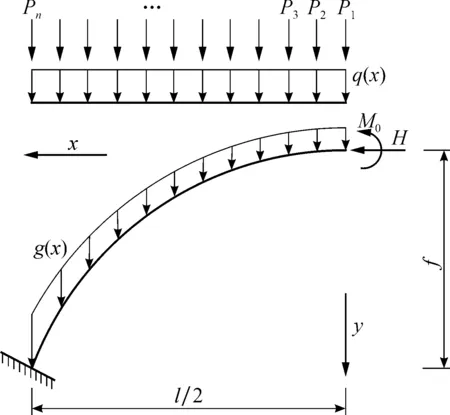
图1 拱圈的受力状态Fig.1 Stress state of arch
为了将沿弧长分布的拱圈自重荷载g(x)与桥面系均布荷载q(x)统一到同一坐标系, 需将g(x)转换为沿跨度方向的荷载gx(x), 则有

(1)
式中:x、y为拱圈任意点坐标。此时作用在拱圈上的全部恒载转换为沿跨度方向全部恒载f(x), 则有
(2)
1.2 拱轴线初始方程的建立
设拱轴线方程为级数函数

(3)
取距离拱顶O点x处的任意截面, 对其右侧的全部荷载对该截面建立弯矩平衡方程, 得拱圈任意截面弯矩M(x)为

(4)
式中:H为拱顶水平推力;M0为拱顶弯矩。

M(Xi)=0;
(5)
将边界条件x=l/2,y=f代入式(2)得
(6)
式(5)与式(6)联立成一方程组, 共有n+2个方程, 其中包含a1、a2、…、an、H、M0共n+2个未知数, 求解该方程组即可得到拱轴线系数以及水平推力和拱顶弯矩, 分别记为a1, 0、a2, 0、…、an, 0、H0和M0, 1, 所得拱轴线称为初始拱轴线
(7)
该拱轴线初始方程采用有限元分析软件对初始拱轴线进行建模计算, 读取各节点的竖向位移, 并运用最小二乘法将其拟合为拱轴线位移函数v(x)。
2 拱轴线最终方程的求解
2.1 迭代式的建立和求解
为了表达挠度与拱轴线及其他参数之间的关系并建立迭代式, 在小变形假设的前提下, 结合拱的挠度理论控制方程[15]

(8)
式中:ω(x)为任意点挠度;E(x)I(x)为抗弯刚度。
由式(2)、 (4)、 (8)可得
(9)
(10)
式中:φ为拱轴线位移函数v(x)与ω(x)的夹角。
将式(10)写成迭代格式则有
(11)
其中:m为迭代次数。
(12)

(13)

与前文相似, 对式(12)与式(13)构成的n+2元方程组进行求解, 即可得到第m+1次状态的拱轴线系数a1,m+1、a2,m+1、…、an,m+1以及水平推力Hm+1和拱顶弯矩M0,m+1。
2.2 迭代终止准则及拱轴线最终方程
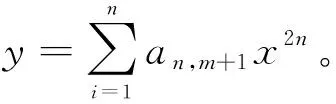
3 算 例
3.1 等截面空腹式拱桥
对跨径500 m的等截面空腹式拱桥, 取矢跨比为l/5, 拱圈沿弧长自重荷载集度g=63 kN/m, 桥面恒载q=200 kN/m, 吊杆间距取为10 m, 桥面荷载由吊杆传递给拱圈。为了方便计算, 取n=4, 求得拱轴线初始方程为y=1.581×10-3x2+3.154×10-10x4-2.082×10-16x6+3.630×10-22x8。取ε=0.000 1, 经过迭代计算后的拱轴线最终方程为y=1.566×10-3x2+6.963×10-10x4-3.396×10-15x6+1.369×10-20x8。
采用Midas Civil软件建立初始状态和最终状态拱轴线的计算模型, 弯矩和应力如图2所示。初始状态下, 拱顶、 拱脚弯矩为29 345.6 和-52 245.1 kN·m, 最小和最大应力为112.449和158.389 MPa; 最终状态下, 拱顶、 拱脚弯矩为35 696.4和-41 219.3 kN·m, 最小和最大应力为109.935和152.386 MPa。经过迭代计算后拱圈内力和应力均得到有效改善, 拱脚弯矩降低21.1%, 全拱最大应力减小3.8%, 最小应力减小2.2%。
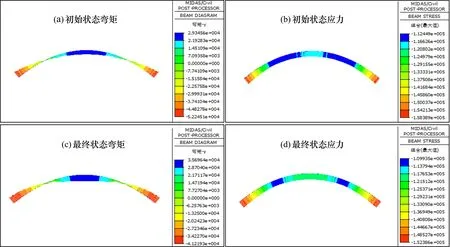
图2 等截面空腹式拱桥初始状态和最终状态下拱轴线的弯矩和应力图Fig.2 Bending moment and stress diagrams of arch axis in initial state and final state of equal section hollow arch bridge
3.2 变截面空腹式拱桥
对跨径500 m的变截面空腹式拱桥,拱圈矢跨比取l/5,拱圈拱顶自重荷载集度gd=73.4 kN/m,拱脚自重荷载集度gd=98 kN/m,沿跨度按线形变化,桥面恒载q=200 kN/m,吊杆间距取为10 m,桥面荷载由吊杆传递给拱圈。为了方便计算,取n=4,求得拱轴线初始方程为y=1.545×10-3x2+1.114×10-9x4-6.115×10-15x6+3.964×10-20x8。取ε=0.000 1, 经过迭代计算后的拱轴线最终方程为y=1.547×10-3x2+1.960×10-10x4+2.403×10-14x6-2.170×10-19x8。
采用Midas Civil软件建立初始状态和最终状态拱轴线的计算模型, 弯矩和应力如图3所示。初始状态下, 拱顶、 拱脚弯矩为35 456.0和-100 322 kN·m, 最小和最大应力为86.373和116.819 MPa; 最终状态下, 拱顶、 拱脚弯矩为38 309.3和-91 821.3 kN·m, 最小和最大应力为86.069和114.402 MPa。经过迭代计算后拱圈内力和应力均得到有效有效改善, 拱脚弯矩降低8.5%, 全拱最大应力减小2.1%, 最小应力减小0.4%。

图3 变截面空腹式拱桥初始状态和最终状态下拱轴线的弯矩和应力图Fig.3 Bending moment and stress diagrams of arch axis in initial state and final state of variable cross section hollow arch bridge
3.3 新型拱轴线与五点重合法拱轴线

图4 悬链线拱轴线弯矩(a)和应力(b)Fig.4 Bending moment(a) and stress(b) of catenary arch axis
3.4 新型拱轴线与悬链线拱轴线
在桥梁设计中, 选取悬链线作为拱轴线时也可在原有五点重合法所求出拱轴系数m的基础上再对m进行调整以找出更为合适的拱轴系数, 在3.2节工况下选取拱轴系数为m=1.1、 1.2、 1.3的悬链线与本文新型拱轴线进行对比, 各节点坐标如表1所示(坐标系见图1), 初始状态拱轴线坐标介于拱轴系数为1.1和1.2的悬链线之间, 最终状态拱轴线坐标介于拱轴系数为1.2和1.3的悬链线之间。同样建立拱轴系数为1.1、 1.2、 1.3的悬链线计算模型, 计算结果如表2所示。最终状态的拱轴线内力及应力相比所选取的悬链线有较大改善, 其拱脚弯矩及最大应力均小于拱轴系数m为1.1和1.2的悬链线; 其拱脚弯矩及最大应力虽大于拱轴系数为1.3的悬链线, 但该悬链线最大应力出现在拱顶, 这对结构受力显然是不利的。

表1 拱轴线坐标

表2 拱轴线弯矩及应力
4 结 论
本文提出了一种新型拱轴线并对其进行深入的分析与研究, 得出以下结论:
(2)给出了迭代计算的终止准则, 当迭代误差|ai,m+1-ai,m|≤ε时(ε为一很小的正数), 即认为计算收敛, 停止迭代计算, 即可得到拱轴线最终方程的系数。
(3)为了对本文的计算理论进行验证, 取n=4,ε=0.000 1, 分别对等截面空腹式拱桥和变截面空腹式拱桥拱轴线进行求解, 并运用有限元分析软件对所得拱轴线进行建模分析。结果表明, 经过迭代计算后, 最终状态的拱轴线在恒载作用下其拱脚弯矩和全拱最大应力均小于初始状态的拱轴线。
(4)将所求得等截面空腹式拱桥拱轴线与五点重合法求得的悬链线拱轴线对比, 新型拱轴线的内力和应力均得到有效改善, 拱脚弯矩减小21.5%, 全拱最大应力减小3.9%, 最小应力减小2.2%。
(5)将所求得变截面空腹式拱桥拱轴线与拱轴系数为1.1、 1.2、 1.3的悬链线作对比, 其内力及应力状态相比所选取的悬链线有较大改善, 拱脚弯矩及最大应力均小于拱轴系数为1.1和1.2的悬链线; 拱脚弯矩及最大应力虽大于拱轴系数为1.3的悬链线, 但该悬链线最大应力出现在拱顶, 这对结构受力显然是不利的, 故本文的新型拱轴线计算方法要优于目前常用悬链线设计方法。
