顾及共模误差影响的澳大利亚GPS站长时间序列分析
2023-10-23凌聪聪廖超明康传利周聪林杨翼飞张振宇
凌聪聪,廖超明,2,康传利,周聪林,杨翼飞,张振宇
(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006;2.南宁师范大学 自然资源与测绘学院,南宁 530001;3.广西壮族自治区自然资源信息中心,南宁 530028)
GPS基准站是提供全球导航定位、 卫星精密定轨、 动态参考框架维护的重要基础设施, 同时也为大陆构造形变监测、 地震预测、 地球动力学研究积累宝贵的观测数据[1-4]。由于GPS站受仪器、 环境等因素影响, 导致观测结果中含有多种误差, 其中区域GPS站网中存在着一种与时空相关的误差, 被称为共模误差(common mode errors, CME), 因此开展GPS时间序列共模误差分析, 对获取区域地壳现今构造运动特征具有重要意义。
对区域GPS站网共模误差研究已取得许多的成果: 胡守超等[5]对南加州区域GPS站的共模误差进行提取, 发现堆栈法(staking)、 主成分分析(PCA)和Karhunen-Loeve展开(KLE)均能有效提取GPS站网的共模误差; 伍吉仓等[6]、 贺小星等[7]通过结合PCA和KLE方法增强空间滤波稳健性, 有效剔除GPS站网的共模误差, 进而提高GPS站坐标时间序列精度; 马超等[8]使用staking、 PCA、 KLE法对南极半岛地区的GPS站进行了空间滤波, 结果表明PCA滤波效果优于其他两种方法, 滤波后残差时间序列振幅、 RMS都有所减小; 此外, 王健等[9]使用PCA估计并剔除欧洲大区域GPS站网的共模误差, 发现空间滤波后部分站点最优噪声模型发生改变; 刘宗强等[10]对四川23个CORS站坐标时间序列进行研究, 通过堆栈法剔除CORS站的共模误差, 发现空间滤波后的部分站点出现随机游走噪声。由此可见, 对于区域GPS站网共模误差的提取方法已比较成熟, 为基于GPS观测数据开展区域地壳现今构造运动监测研究提供了技术支撑。
目前, 姜卫平等[11]、 汪浩等[12]对澳大利亚区域进行了相关研究, 前者研究时间跨度对GPS站水平方向噪声模型的影响, 后者利用GPS和GRACE数据研究区域地壳垂向季节变化。 本文选择澳大利亚区域19个GPS站长跨度坐标时间序列作为研究对象, 采用PCA方法提取共模误差, 利用谱指数估计和最大似然估计法分析剔除共模误差前后的时间序列噪声特性, 为开展区域地壳现今构造运动特征研究提供高精度坐标速度场估值。
1 分析方法
1.1 主成分分析
主成分分析是一种广义的空间滤波方法, 该方法把一组相关数据变量通过线性变换成一组不相关的变量[6,13]。假设一个区域GPS站网有n个测站, 每个站点观测m天, 且满足n≤m关系。设X矩阵的每一列表示站点某一方向时间序列的残差值, 每一行则表示某一历元所有站点的残差值。X矩阵的协方差阵为B, 其元素定义为
(1)
协方差矩阵B是一个n×n对称矩阵, 可由正交分解为
B=VΛVT,
(2)
式中:Λ是协方差阵B的非零特征值构成的对角矩阵, 其中特征值按对角线降序排序;VT是由特征向量构成一个n×n正交矩阵。根据特征值可得到主成分为
(3)
式中:ak是X矩阵的第k个主成分;Vk为对应第k个主成分的特征向量。以降序排列的前几个特征值代表残差时间序列的最大贡献, 而特征向量代表各站点的空间响应, 则PCA最终提取的CME可定义为
(4)
式中:ε(Mi,j)表示由p个主成分计算的第j个站点第Mi天的共模误差。
1.2 谱指数法
许多地球物理信号能用某种常见的统计模型来表征, 可描述为幂律过程[14-16]。 GPS坐标时间序列噪声信号也属于地球物理信号, 也可描述为幂律过程, 将该随机过程的时间域用功率谱函数描述为
Px(f)=P0(f/f0)k,
(5)
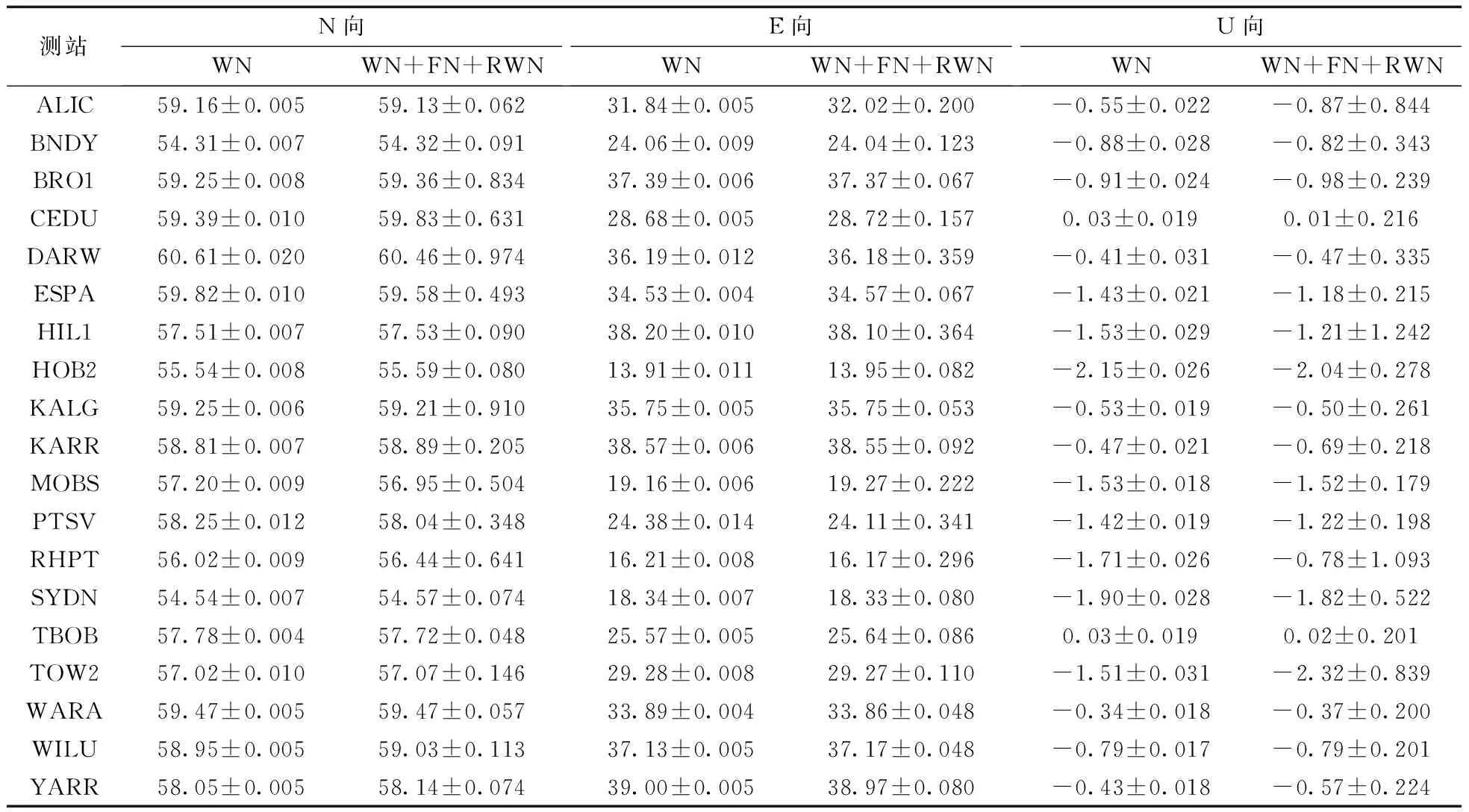
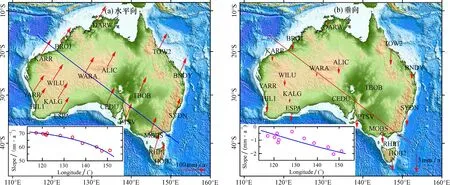
式中:f是时间频率;P0和f0为归一化常数;Px(f)表示功率谱密度;k是频谱指数, 其为双对数坐标系中功率谱密度P0(f)对频率图像的斜率, 取值在[-3,1]。 当-3 借助CATS时间序列分析软件[17]采用最大似然估计法计算最大似然值(MLE), 同时估计噪声分量值。对于给定的一组观测值x, 使其协方差的联合概率值l达到最大 (6) 对式(6)两边取对数 MLE=ln[l(x,C)] (7) 其绝对值是反映噪声模型的一个关键指标, 可通过其估计出不同噪声模型的最大似然值, 选取其中最大MLE的模型作为最佳模型。蒙特卡罗提出, 两种噪声模型MLE差值大于2.9可作为噪声模型的区分阈值[10], 即假设WH+RWN与WH+FN的MLE差值大于阈值2.9, 则可判定MLE大的噪声模型更优。 选取均匀分布于澳大利亚地区的19个GPS站(图1)、 时间跨度为2010-06—2020-07的坐标时间序列数据, 数据来源于内达华大地测量实验室(http: //geodesy.unr.edu/gps_timeseries/)[18]。原始时间序列数据采用GIPSY/OASIS-II软件进行处理, 同时已对电离层、 对流层延迟、 天线相位中心偏差进行校正, 并加入了极潮、 海潮及固体潮等模型改正, 最终处理得到IGS14框架下GPS站坐标时间序列。 图1 澳大利亚区域19个GPS站点序号及分布Fig.1 Distribution of 19 GPS stations in Australia 为了合理估计GPS时间序列各项参数,需要对其进行预处理。一般GPS时间序列模型可表示为 y(ti)=a+bti+csin(2πti)+dcos(2πti)+esin(4πti)+ (8) 式中:ti表示以年为单位的时间; 待求系数a、b分别表示为测站的初始位置和速率; 系数c、d表示站点周年项运动; 系数e、f表示站点半周年项运动;gi为由各种原因(如仪器天线更换等)引起阶跃式坐标突变;H为一阶梯函数;Tgj为发生坐标跳变时间;vi为观测误差项。 受到外界条件、 GPS接收机软硬件等因素影响, 部分GPS站点某些年积日会出现观测数据丢失或观测数据质量不好等情况, 从而导致 GPS 时间序列存在缺失或粗差等问题。本文首先采用绝对中位数法对每个站点的时间序列进行粗差剔除; 然后用三次多项式进行插值与补齐缺失数据, 得到等间隔的“干净”时间序列; 最后对原始时间序列去均值项、 速度项以及阶跃项, 得到各GPS站点的残差时间序列。ALIC站点原始坐标时间序列经过预处理后得到的残差时间序列如图2所示。 图2 ALIC站点残差时间序列Fig.2 Residual time series of Station ALIC 对澳大利亚地区19个站点的残差时间序列进行主成分分析, 分别得到N、 E、 U向的贡献率, 结果如图3所示。可知, 采用PCA分析得到第一主成分贡献率在N、 E、 U向为36.9%、 42.7%、 39.9%; 第二主成分贡献率在N、 E、 U向为22.1%、 16.4%、 9.6%; 第三主成分贡献率在N、 E、 U向为7.9%、 8.4%、 8.8%; 前3个主成分累计贡献率在N、 E、 U向66.9%、 67.5%、 58.3%, 即前3个主成分综合了大部分的空间响应, 因此后续仅对前3个主成分进行讨论。 图3 N、 E、 U方向的主成分贡献率占比Fig.3 Contribution of principal components in N,E and U direction 研究表明, 当某一主分量模式中50%以上测站的标准化空间响应大于25%, 且该模式的特征值贡献率大于1%, 则可作为测站间的共有模式[19]。为确定式(4)中的主分量个数p来计算CME, 将特征向量除以其绝对值最大的元素, 得到标准化的空间特征向量, 如图4所示。第一主分量每个站点N、 E、 U方向上的标准化空间响应均大于25%, 主成分贡献率超过1%, 而第二、 三主分量在3个方向上并不满足该条件, 因此本文用第一主成分来计算区域各站的CME。以ALIC站为例, 扣除了CME前后的残差时间序列和残差RMS分别如图5、 6所示。 图4 各GPS站点标准化空间响应Fig.4 Standardized spatial responses of GPS stations 图5 ALIC站滤波前后的残差时间序列Fig.5 Residual time series before and after filtering at Station ALIC 图6 各站点滤波前后的残差RMS值Fig.6 Residual RMS of each station before and after filtering 从图5可看出, 滤波前残差时间序列N、E向存在较弱的周期波动,U向周期波动明显,滤波后残差时间序列在N、 E、 U向的振幅都有所减小。滤波后各站N、 E、 U向的残差RMS都有减小, 平均减小约29.7%、 25.5%、 24.2%, 说明滤波后各站点的坐标分量估值精度得到有效提高(图6)。此外, 部分站点滤波前后的残差RMS值相差较小, 而部分站点则相差较大, 这可能与站点空间分布有一定关系。如U向站点序号5、 8的残差RMS值相差较小, 对应站点DARW、 HOB2分布于澳大利亚边缘。 用CATS软件获取空间滤波前后的时间序列在N、 E、 U向上的谱指数, 如表1所示。各站点滤波前后的时间序列的谱指数在-2~0, 说明该区测站滤波前后的噪声模型并非单一的白噪声模型。 表1 空间滤波前后测站的谱指数 为确定最优噪声模型, 用CATS软件获取滤波后各测站在WN、 WN+FN、 WN+RWN、 WN+FN+RWN噪声模型下的最大似然值, 并将其他3种模型与WN模型的最大似然值作差, 结果如图7所示。WN+FN和WN+FN+RWN模型MLE差值基本相等, 且两个模型都比WN+RWN模型的MLE差值大。根据蒙特卡罗准则判定WN+FN和WN+FN+RWN模型更优, 但两个模型不具有可分性。现假设WN+FN+RWN为区域最优噪声, 且在该噪声模型下估计滤波前后各站点的噪声分量。 图7 19个GPS测站N、 E、 U向MLE差值Fig.7 MLE difference of 19 stations in N,E,U direction 限于篇幅, 表2仅列出滤波前后的9个GPS站基于WN+FN+RWN模型的噪声分量。可知: 1)澳大利亚地区GPS站N、 E、 U向最优噪声模型为WN+FN+RWN, 9个站的坐标分量出现有白噪声、 闪烁噪声及随机游走噪声, 因此该区域GPS测站在N、 E、 U向不仅需要考虑WN+FN, 还应加入RWN噪声; 2)空间滤波后测站N、 E、 U向白噪声和闪烁噪声的估值都有减小, 但U向有部分站点(ALIC、 TBOB)的白噪声有增加情况, 该原因有待进一步研究; 3)部分站点(ALIC、 KARR等)空间滤波后还原出了被掩盖的随机游走噪声, 这表明空间滤波能够将被高频信号掩盖的随机游走噪声显示出来。 表2 基于WN+FN+RWN模型的噪声分量估计值 根据GPS站时间序列分析结果, 采用WN、 WN+FN+RWN模型分别估计GPS站N、 E、 U向的速度及其精度, 如表3所示。可知, 模型WN+FN+RWN和WN在N、 E、 U向速率平均偏差为0.12、 0.06、 0.19 mm/a, 最大差值分别为0.42、 0.18、 0.93 mm/a。在速度不确定性方面, 最优噪声模型估计下N、 E、 U向速度不确定性为WN模型下的十至几十倍。由此说明, 仅考虑白噪声的影响并不能真实地反映测站速度及其不确定性, 尤其是对于速度不确定性的估计。 从内达华大地测量实验室收集到的站点速率与WN+FN+RWN模型估计站点速率作差, 得到GPS站的速率差值(图8)。由19个GPS测站点N、 E、 U向速率差异可知, GPS站点N、 E、 U向速率差异范围-0.99~0.19 mm/a、 -0.39~0.73 mm/a、 -1.74~1.25 mm/a, 差异绝对值的均值分别为0.28、 0.17、 0.45 mm/a。基于WN+FN+RWN模型估计的GPS站坐标速率与内达华大地测量实验室处理的结果相比较, 从整体上具有较好的一致性, 其差异主要表现在HIL1、 RHPT、 TOW2站点的垂向速率估值; 同时, 这3个站点速率估值的不确定性相对较大, 分别达到了±1.24、 ±1.09、 ±0.84 mm/a(表3)。 表3 WN+FN+RWN模型与WN模型下的GPS站速度及其精度 图8 GPS站点N、 E、 U方向速率差Fig.8 Rate difference of GPS stations in N,E and U direction 以WN+FN+RWN组合模型下N、 E、 U向的速率绘制澳大利亚板块坐标速度场, 同时绘制辅助线上下10°范围的GPS站速率子图。由图9a和表3分析可知, 测站N向速率在54.3~60.5 mm/a, E向速率在13.9~39.0 mm/a, 测站水平方向速率的差异较大, 说明澳大利亚板块内部存在一定形变。IGS14框架下GPS站整体水平运动方向为北东方向, 平均速率约为65.1 mm/a; 在太平洋海板块西南端的北西向推挤力、 东南印度洋中脊的北东向分离推挤力作用下, 测站运动方向由北北东逐渐向北方向过渡; 自澳大利亚地区的北西向南东方向, 水平速率估值逐渐减小。 图9 WN+FN+RWN模型下的澳大利亚水平(a)与垂直(b)速度场Fig.9 Horizontal(a) and vertical(b) velocity fields based on WN+FN+RWN model in Australia 除TBOB、 CEDU站点近零速率的正值外(图9b、 表3), 其余站点速率为-2.15~0 mm/a, 各GPS站点垂向速率差异较小。GPS站点监测到澳大利亚板块现今地壳垂向运动整体处于缓慢下沉状态, 平均速率约为-0.95 mm/a; 澳大利亚地区的东、 南面下沉速度相对于西、 北面更快。 通过分析滤波前后和不同噪声模型下澳大利亚地区19个GPS站2010-06—2020-07的长时间序列, 得到以下结论: (1)对区域GPS站开展空间滤波能够有效降低白噪声和闪烁噪声。此外, 空间滤波能够将被掩盖的随机游走噪声还原出来, 因此应考虑对该区域进行空间滤波。 (2)澳大利亚地区GPS站坐标时间序列应考虑采用WN+FN+RWN的组合。虽然白噪声模型与WN+FN+RWN模型的速率估值非常接近, 但只考虑白噪声影响下的速度不确定性将被低估。因此, 在该区域开展GPS站时间序列分析时, 应考虑采用多噪声组合模型代替白噪声模型。 (3)在IGS14框架下, 澳大利亚区域19个GPS站现今地壳水平运动方向整体表现为北北东向, 平均速率约为65.1 mm/a, 且速率自北西向南东逐渐减小; 垂直运动处于缓慢下沉状态, 平均速率约为-0.95 mm/a, 且东、 南面下沉速率相对于西、 北面更快。1.3 最大似然估计法

2 数据来源与预处理
2.1 GPS数据
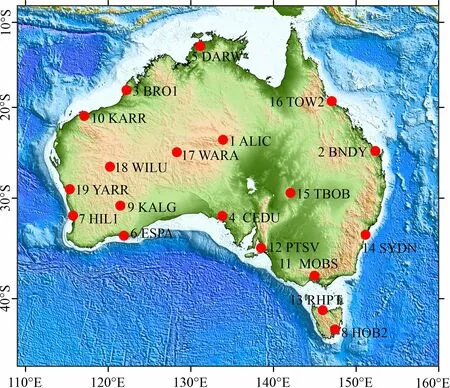
2.2 GPS时间序列处理

3 GPS站坐标时间序列噪声特性分析
3.1 共模误差提取
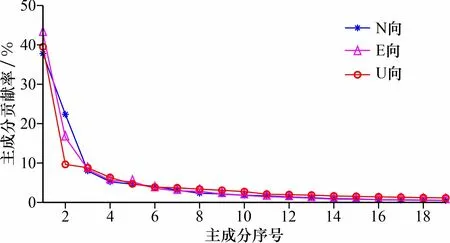



3.2 最优噪声模型分析



4 区域坐标速度场分析
4.1 基于WN+FN+RWN模型的坐标速度场估计

4.2 区域构造运动分析
5 结 论
