考虑开关矩阵的综合化航电系统任务可靠性分析
2023-10-23王道震李翼瀚刘红波马玉柱王锋
王道震,李翼瀚,刘红波,马玉柱,王锋
(天津七一二通信广播股份有限公司,天津 300462)
引言
在航电综合射频系统中,涉及到多路信号的综合集成设计,需要进行通道切换。因此,综合射频架构设计需要用到开关矩阵以实现功能重构。开关矩阵不仅重要而且复杂,因此在任务可靠性建模时不能将其忽略。当开关矩阵的失效率增大到一定程度时,旁联模型的优势就不复存在。本文研究重点在于研究任务可靠度的比例门限,它跟系统任务时间有关系。求解开关矩阵与通道失效率的比例门限,并证明小于等于这个比例门限时,在任何系统任务时间内旁联模型的任务可靠性总是大于等于并联模型。
1 综合系统架构中通用激励模块设计
射频综合采用模块化、标准化的设计方法,对各个子系统的各种功能进行重新划分、组合,将传感器前端组件和数据处理组件进行资源共享,可重构的新型系统。射频综合架构是新型航电系统综合的架构(图1),将融合雷达、电子战、通信、导航识别等多个传感器系统的射频部分。由此可见,开关矩阵对射频通道选择起到很重要的作用,而且其组成复杂,不能忽略。
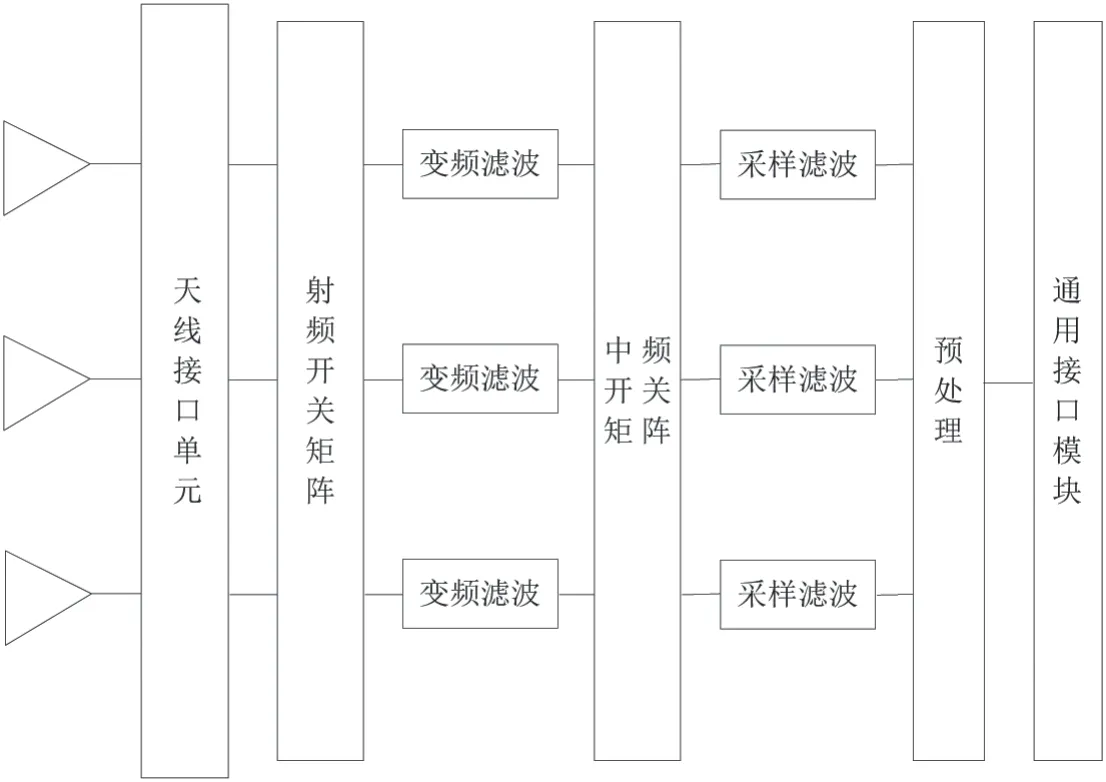
图1 射频综合架构示意图
下面我们将通用资源里的通用激励模块进行说明。通用激励模块内有4个通道,实现上变频及快跳本振产生功能。
2 旁联模型与并联模型的对比分析
2.1 考虑开关矩阵失效的马尔科夫过程分析
某综合射频系统中有3个模块,每个模块中有4路相同的通道,且4路通道都正常才能工作,其任务可靠性框图如2所示。因此λ1=λ2=λ3=λ11+λ12+λ13+λ14=λ21+λ22+λ23+λ24=λ31+λ32+λ33+λ34。

图2 考虑开关失效率的旁联模型任务可靠性框图

图3 通用激励模块状态转移图
当考虑开关失效率时,我们研究一下开关的失效率与通道失效率之间满足一定条件时,旁联的任务可靠性优于并联的任务可靠性。
马尔科夫过程是一类随机过程,它最早由俄国数学家马尔科夫在1907年提出。它假设这个模型的每个状态只依赖之前的状态。
利用马尔科夫过程建立可靠性模型有以下几点假设:
1)系统的各个单位寿命和维修时间服从指数分布;
2)在时间区间(t,t+Δt)内,发生故障的概率为λΔt;
3)在时间区间Δt内出现2次以上的概率或修复的概率为0,因为Δt足够小且三个模块之间相互独立。
S1: 三个激励模块均正常,第一通路检测及转换开关正常且第一个激励模块工作。
S2:第一个激励模块故障或该通路检测及转换开关失效,第二通路检测及转换开关正常且第二个模块工作。
S3:第一个激励模块故障,第二个激励模块故障或该通路检测及转换开关故障,第三通路检测及转换开关正常且第三个模块正常工作。
S4:三个激励模块均故障。
第一个模块的故障率为:λ1,第二个模块的故障率为:λ2,第三个模块的故障率为λ3。由于三者模块是相同的,因此失效率相同设为λ,每路检测及转换开关的失效率为λk。
P(t)为处于各个状态概率的列矩阵:
微系数矩阵P(∆t)为连续型马尔科夫过程,其转移概率为t和t+∆t之间极小的∆t时间内的概率。
根据导数定义得:
借鉴现代控制理论中状态方程的求解方法,将时域转换到复频,将上式进行拉普拉斯变换得:
然后再将上式进行反拉普拉斯变换得:
系统初始状态为S1即:
状态转移矩阵P:
每一行的概率和为1。
A=P-I;
计算S1、S2、S3状态下的概率:
2.2 并联模型的任务可靠性分析
并联系统没有开关矩阵时,其可靠度模型及MTBF求解公式如图4所示。

图4 通用激励模块并联任务可靠性框图
令λk=k*λ(k>0)
当MTBF旁=MTBF并,求解方程得k=1.4。
显然k<1.4时,则∆MTBF大于0,即旁联的平均严重故障间隔时间大于并联。下面我们讨论任务可靠度,两种模型的差值。
如图5所示,横轴取任务时间零到十万小时,纵轴取旁联模型的任务可靠度减去并联模型的任务可靠度得到的曲线。

图5 开关矩阵失效率为通道的1.4倍时任务可靠度差值
由图5可知,根据不同的失效率迭代仿真计算,在开关矩阵的失效率为通道失效率的1.4倍时,得到如下结论。
任务可靠度:在考虑开关矩阵失效率为通道失效率的1.4倍时。由上图可知当系统任务时间t大于1.81e4时,旁联的任务可靠度大于等于并联的任务可靠度。大于等于1.81e4之后旁联的任务可靠度小于并联的任务可靠度。
下面我们探索在一个适当的比值下,无论系统任务时间t取何值,总能使得带开关的旁联系统的任务可靠度总大于等于并联系统的任务可靠度。
将R旁-R并消掉e-λt的系数部分,则有(k+1)2/k2=3,因此得到k=(√3+1)/2,此时有如下等式:
为方便比较大小,将其转为以下分式形式:
设分子部分为m,分母部分为n则,
当λt>0时,
分别对m和n求解二阶导数:
当λt→0+时,依据洛必达法则
综上所述:将分子分母分别求二阶导数则有m"≥n"且在λt趋近0+时,m'=n',因此在定义域上有m'≥n'。由于λt趋近于0+时,分子分母m=n,因此在定义域上总有m≥n,即R旁≥R并。
根据不同的失效率迭代计算,只要开关矩阵的失效率为通道失效率的倍,总能得到如下结论,即随着任务时间t增大,旁联部分与并联部分的任务可靠度差值越来越趋近于0,并且旁联模型的任务可靠度不小于并联模型的任务可靠度。为严谨起见,为证明其为比例系数门限,取其两侧的1.366和1.367为例进行数值模拟。由于两个数非常相近,二维图像上不便于区分,因此建立了三维图像模型,X轴为任务时间t,Y轴为比例系数K,Z轴为任务可靠度的差值。如图6所示,当取k值为1.366时,Z轴全为非负数。当取k值为1.367时,在系统任务时间取7e4时Z轴为负值,进一步证明了k=作为比例门限的正确性。
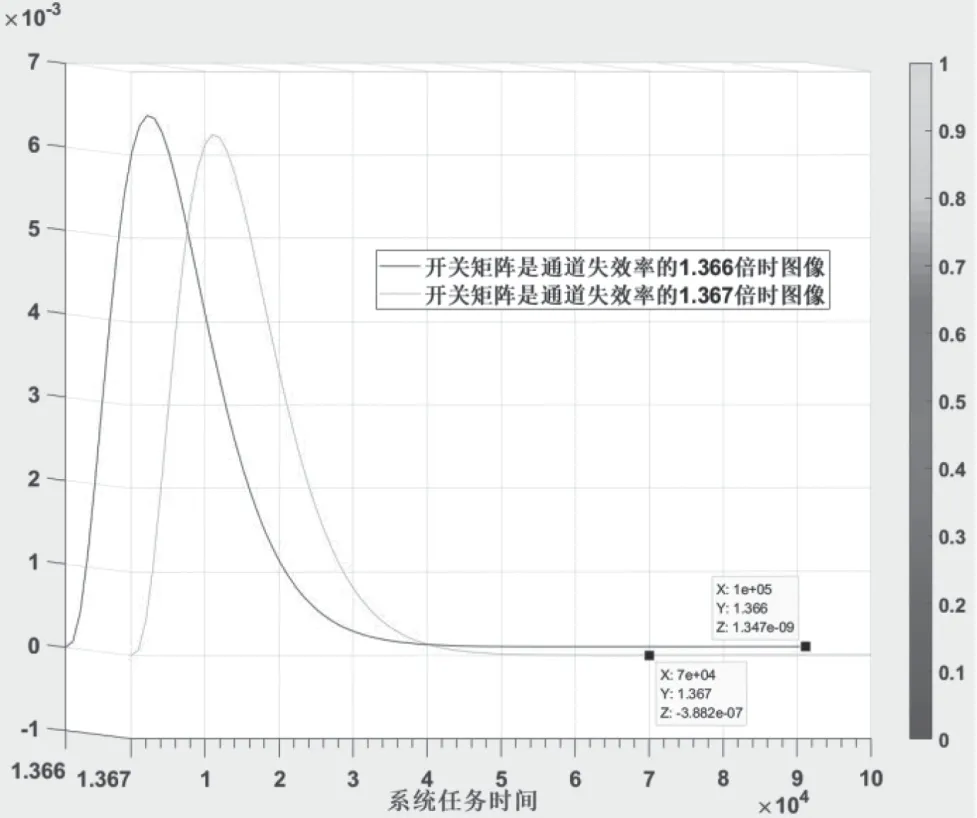
图6 取比例门限两侧K值时旁联与并联的任务可靠度差值
3 结论
在航电系统中通过任务可靠度和平均严重故障间隔时间的计算,比较旁联和并联模型的优势。
当开关矩阵失效率小于等于通道失效率的1.4倍时,旁联模型的平均严重故障间隔时间(MTBCF)大于等于并联模型;同理,当开关矩阵失效率大于通道失效率的1.4倍时,旁联模型的平均严重故障间隔时间(MTBCF)小于并联模型。当开关矩阵失效率小于等于通道失效率的()/2倍时,旁联模型在任何系统任务时间内的任务可靠度大于均大于等于并联模型。这个结论对于方案设计决策提供依据,即要不要加开关矩阵,在任务可靠性角度上来讲,需要考虑开关矩阵与通道的失效率比例关系,否则旁联模型的任务可靠性反而会降低。
