两阶段遗传算法和贪心策略相结合的多约束排样优化方法

马英钧，钟俊江

（厦门理工学院数学与统计学院，福建 厦门 361024）

排样优化问题本质上也称切割填充问题，优化的目的是合理规划方形产品在板材上的布局，减少下料过程中的板材浪费，简化切割过程。下料作为众多制造企业生产链中产品及零部件生产的第一道工序，消耗的材料和资源不容小觑，如何提高材料利用率，降低原材料消耗，是企业减少资源和能源浪费，承担环境保护责任所要解决的关键问题。

针对排样优化问题，当前已提出一些计算模型。王竹婷等［1］将层次聚类思想引入矩阵排样优化问题中，通过计算矩形组件间的结合度，将结合度最高的组件进行合并，并重复该过程来实现优化方案设计。王伟等［2］提出了一种基于捕食策略的遗传算法，通过对编码、遗传算子和适应度算子进行改进，并结合最低轮廓线搜索算法来获得最优布局。曾晓亮等［3］利用六元数组对矩形组件进行表征，并利用多岛遗传算法来设计排样方案，结果表明，该方案具有较高的利用率和稳定性。近年来，陈仕军等［4］提出反悔算子、距离受限邻域算子、满足容忍度3种策略来改进传统的邻域搜索算法，通过与以往方法的结果对比发现，该方法具有很高的求解效率。吴继聪等［5］介绍了多种Meta-Heuristic 算法在排样优化研究中的应用，并分析不同算法的性能和适用场景。与之前的方形组件的排样优化研究不同，张闯等［6］研究二维椭圆零件的排样优化问题，提出了一种在仿射坐标系下的变换，并建立整数规划模型。以上成果虽然推动了排样优化问题的研究，但是它们仅考虑如何排样以使材料最省，很少考虑到机器的具体切割限制，比如每次的切割可以保证板材分离及切割的次数不能过多的限制等。基于此，针对多约束排样优化问题的特点，本文提出了一种两阶段遗传算法和贪婪策略相结合的排样优化方法，建立产品布局和条带布局的数学模型，利用一种两阶段遗传算法来进行模型求解，并设计有效的解码方案提升模型的求解效率。同时，为了进一步提升利用率，针对“条带余料”和“板材余料”建立2种基于贪婪策略的算法模型，并在多个数据集上执行计算，以验证本文算法的有效性。

1 问题分析

本研究的问题引自2022 年“中国光谷·华为杯”研究生数学建模竞赛B 题第一问。本问题中的切割需要满足以下条件：1）只考虑“齐头切”的切割方式（直线切割、切割方向垂直于板材一条边，并保证每次直线切割板材可分离成2块）；2）切割阶段数不超过3，同一个阶段切割方向相同；3）假定板材原片仅有一种规格且数量充足；4）排样方案不用考虑锯缝宽度（即切割的缝隙宽度）影响；5）最终切割生成的产品项是完整的，非拼接而成。图1是一种有效的3阶段切割方式及其生成的模块。

图1 一种3阶段切割方式及其生成模块简图Fig.1 A three-stage cutting mode and modules it generated

图1 中：实竖线表示第一次切割得到两个模块分别是条带1 和条带2；长横虚线表示对于条带的切割（即第二次切割）得到6个栈分别是栈1、栈2、栈3、栈4、栈5和栈6；短竖虚线表示对于栈的切割（即第三次切割）最终获得17个产品。由图1可以看出，以上的每次切割都是沿着板材的一条边进行的，并且每次切割都将板材分成2段。对于该问题直接进行二维布局，不仅计算复杂度高，而且很有可能导致不满足“切割阶段不超过3” 的约束。由图1可知，第二刀切割会产生多个栈，每个栈都是由边长相等的产品组成的，因此，研究等边长的产品可以在一定程度上提升板材的利用效率。

为了减少切割的次数，先将边长相等的产品拼接为条带，并将条带沿着板材的长边放置。因此，根据产品的边长特点，将其分为3个类别：1）类别1包含有相等的边长，并且相等边长小于W（板材的宽）的产品；2）类别2 包含边长大于W的产品；3）类别3 包含与其他产品的边长都不相等的产品。对于类别1，建立一阶段模型来实现产品组合为条带优化；对于类别1 得到的条带和类别2 的产品（每个作为一个条带），建立二阶段模型来实现条带在板材上的布局优化；对于边长不相等的产品（类别3），利用前两步的废料和新板材，执行余料再利用。具体求解框架见图2。

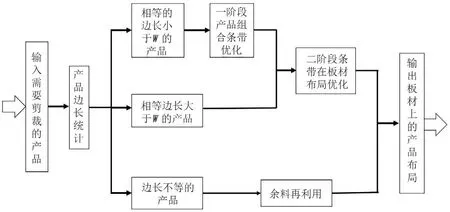
图2 多约束排样优化问题的整体求解框架Fig.2 Solution framework for multi-constraint layout optimization

2 基于两阶段遗传算法的产品布局优化

本节主要通过两阶段遗传算法来实现类别1 和类别2 的产品在板材上的优化布局，主要包含3 个步骤：1）建立产品组合优化数学模型；2）建立条带优化数学模型；3）构建两阶段遗传算法来初步实现两类产品在板材上的最优布局。

2.1 产品组合优化数学模型的建立

对于物品很少的分组，如果直接组合为条带，可能会导致空间的浪费。因此，设置阈值ε，对边长相等的物品数大于ε的那些分组拼接为条带。

令M1表示需要拼接的物品的个数，li表示第i产品的另一边（除了相等边长的另一边）的长度，M2表示预估需要的条带个数，xij表示第i产品是否放置于条带j中，当第i产品置于条带j中时，xij=1，反之，xij=0。为了使得用料最省，要求在不超过每个条带的限制长度L（板材的长边）情况下，使得所用的条带的数量尽可能少。此时，其模型为

需要注意的是，以dataA1的边长为58的产品为例，其84个产品另一边长的总和为100 830，而每个条带的最大长度为2 440，因此，M＞100 830/2 440 ≈41.32。对于式（1）描述的混合0～1 规划问题，变量的个数至少为84 × 42。

2.2 条带组合优化数学模型的建立

式（2）中：δ(x)为判断函数，与式（1）中的定义类似。由式（2）可以看出，目标函数要求选取的板材数尽可能小。第一个约束条件要求每个板材剪裁的条带的总宽度小于板材的宽度W，第二个约束要求每个条带必须有一个板材来剪裁，第三个约束条件要求yij是0～1决策变量。

需要注意的是，以dataA1 和阈值ε=10 为例，根据类别1 拼接得到108 个条带和类别2 的102 个条带，一共得到210 个条带。这些条带的总宽度为71 754，因此，至少需要的板材数量N=71 754/1 220 ≥59。也就是说，式（2）描述的模型中决策变量的个数至少为210 × 59。

2.3 基于两阶段遗传算法的模型求解

节2.1 和节2.2 描述的问题都是混合0～1 规划模型，并且模型中决策变量的个数都比较多，利用传统的优化方法很难求解，甚至很难得到可行解。基于此，本研究采用遗传算法进行求解。现以产品组合优化的求解进行介绍。

遗传算法的优化方案包含编码、生成初始种群、计算适应度、交叉、变异等操作。

1）编码。为了提升编码效率，本研究使用序号编码来生成染色体。对于M个产品，任意一条染色体可表示为X={x1，x2，…，xM}，其中{x1，x2，…，xM}表示产品编号{1，2，…，M}的任意排列。染色体X表示的意义是依次实现产品x1，x2，…，xM的剪裁。

2）目标函数。对于染色体X={x1，x2，…，xM}，条带的长度限制L，产品另一边长度{l1，l2，…，lM}，计算条带总数的计算步骤如下：

Step1将产品项按照染色体X={x1，x2，…，xM}的顺序排列；初始化K=0，i=1，j=1，F1=∅，Z=0。

Step2将当前第i个产品放入Fj中，即Fj={Fj，xi}，并计算Z=Z+lxk。

Step3当Z≤L时，表示前条带有剩余；否则，删除集合Fj的最后一个元素，选择下一个条带，即j=j+1，Fj={xi}，Z=0。

Step4i=i+1，若i≤M，执行步骤Step2和Step3；否则，返回需要的条带总数K=j。

在以上步骤中，集合Fj表示第j条带剪裁的产品集合，K表示条带总数。由以上步骤可以看出，解码步骤的算法复杂度为O(n)。本研究中的每个染色体都是利用贪心算法进行解码，不仅保证每个染色体是可行解，而且是局部最优的。

3）交叉和变异。由于本文采用序号编码，在交叉的时候可能会导致染色体损坏。因此，采用部分交叉映射来对染色体进行修正［7-9］。部分交叉映射的主要思想是：对两个待交叉染色体交叉区域内的基因互换，并利用交叉区域内的映射关系将交叉区域外的基因进行修正。为了提升计算效率，保证变异之后染色体的有效性，变异操作采用基因交换的方式，即随机选择待变异染色体两个位置的基因进行交换［10］。

4）重组。为了提升算法效率，保证优秀染色体可以进入下一代，本文设置代沟操作，并在每一次交叉变异之后，选取上一代最优的10%的个体直接进入下一代。

遗传算法的具体流程见图3。

图3 遗传算法流程图Fig.3 Genetic algorithm flow

综上，首先利用遗传算法求解节2.1的问题来获取产品组装为条带的最优方案，然后再利用遗传算法求解节2.2实现条带在板材上的最优布局。

3 基于贪心策略的余料再利用

在产品组合优化和条带组合优化的过程中，都可能会出现余料，合理利用这些余料可以在很大程度上提升板材的利用效率。因此，基于贪心策略［11-12］，本文提出两方面的余料利用策略，即产品组合的余料再利用和条带组合的余料再利用。

3.1 产品组合的余料再利用

条带剪裁产品的过程中，若条带中产品项的总长度小于L，导致余料S1产生。图4 给出了余料S1的再利用示意图。

图4 余料S1的再利用示意图Fig.4 Reuse of residual material S1

如图4所示，对于组装条带产生的余料S1，其高为h1，宽为w1，从剩余的产品中选择可以放入S1的产品集合，即={x|min {hx，wx}＜min {h1，w1}且max {hx，wx}＜max {h1，w1}}。从集合中选择面积最大的产品C1进行放置，为保证切割总数不超过3 的约束，C1的左下角必须与余料S1的左下角重合。此时，如图4两边的两个图所示，由于C1的摆放方式不同，可得到不同的可使用余料分别为和，容易看出余料可使用面积更大，因此，按照图4 中最右图的方式摆放。余料S1的再利用步骤如下：

Step1令余料S1的宽为w、高为h，且剩余m个需要剪裁产品{C1，C2，…，Cm}的宽分别为{w1，w2，…，wm}，高分别为{h1，h2，…，hm}，当前可用产品集合T=∅。

Step2当min{w，h}＞min{wi，hi} 且 max{w，h}＞max{wi，hi}，说明此时第i个产品项可利用余料S1剪裁，更新T={T，i}。

Step3i=i+1，若i≤M，执行步骤Step2；否则，执行Step4。

Step4从T中挑选面积最大的第k产品放入余料S1中，且保证该产品左下边顶点与S1左上顶点重合，计算此时可用余料。

Step5计算产品旋转90o后的可用余料，当旋转后依旧可以放置，并且＞S′1时，将该产品旋转90o，更新余料S1=，更新余料S1的宽w′和高h′，T=∅；否则，更新余料S1=，更新余料S1的宽w′和高h′，T=∅。

Step6更新步骤Step2、Step3、Step4 和Step5，直至不能找到可放置的产品。返回关于当前余料S1的再利用方案。

根据以上步骤可以看出，对于任意产品的放置，都需要对所有的可能产品遍历一次，因此，其算法复杂度为O(n2)。

3.2 条带组合的余料再利用

在板材剪裁条带的过程中，若板材中条带的总宽度小于W，导致余料S2产生。余料S2的再利用示意图见图5。

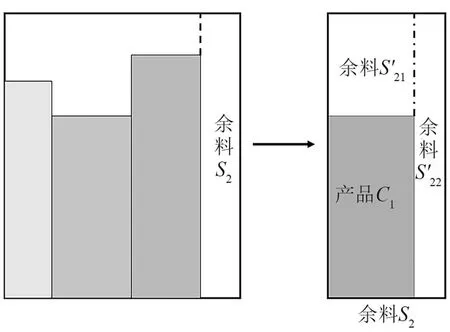
图5 余料S2的使用示意图Fig.5 Reuse of residual material S2

板材剪裁条带过程中产生的余料如图5所示。首先，利用贪心策略，从剩余需要剪裁的产品中选择最优的，即满足剪裁要切，面积最大，且放置方式要保证可利用余料的可利用面积最大。然后，经过第一次放置，有2块余料产生，即余料和余料。对于余料的处理方式与第一步类似，而余料的处理方式如节3.1余料S1的再利用步骤所示。余料S2的再利用步骤如下：

Step1令余料S2的宽w和高h，且剩余m个需要剪裁产品{C1，C2，…，Cm}的宽分别为{w1，w2，…，wm}，高分别为{h1，h2，…，hm}。

Step2按照余料S1的再利用算法，寻找产品放入S2中，得到剩余余料和余料。

Step3对剩余余料，重复余料S1的再利用算法，直至不能放置产品。

Step4对剩余余料，重复步骤Step2和Step3，直至不能放置产品。输出余料S2的再利用方案。

4 模型整体求解结果和分析

4.1 两阶段遗传算法的优化性能分析

对于类别1和类别2中的产品，利用两阶段遗传算法来获得产品的初始布局。现以dataA1中边长为58 的84 个产品组合条带和210 个条带组合在板材上布局为例来分析两阶段遗传算法的优化性能，结果见图6。

图6 关于dataA1的两阶段遗传优化过程图Fig.6 Two-stage genetic optimization process for dataA1

由图6（a）可以看出，初始随机方案的条带数为51，条带利用率为100 830/(2 440 × 51)=81.03%。随着算法进行，所需的条带数逐渐降低，最终需要的条带数为46，条带利用率为100 830/(2 440 ×46)=89.83%。条带的数量降低4 个，条带的利用率提升8.81%。由图6（b）可以看出，随着迭代过程的进行，组装210个条带需要的板材数量逐渐降低。初始随机生成的组装方案需要64个板材，板材的横向利用率为71 754/(1 220 × 70)=84.02%，其中71 754为210个条带的总宽度；当迭代次数为150次以后，板材的个数稳定到64个，板材的横向利用率为71 754/(1 220 × 64)=91.90%，提升了7.88%。

4.2 阈值对模型性能的影响

如节2.2所述，对于某些存在边长相等但数量很少的物品，直接组合为条带可能会导致板材的浪费。通过设置阈值ε=2，3，…，20来分析相等边长物品的数量与板材利用率的关系。具体地，当ε=2时，考虑所有存在边长相等的物品（相等边长小于1 220）；当ε=3 时，考虑相等边长的物品数量≥3的情况。以dataA1为例，对于不同的阈值，代入以上过程，可得到相应的板材利用率，结果见图7。

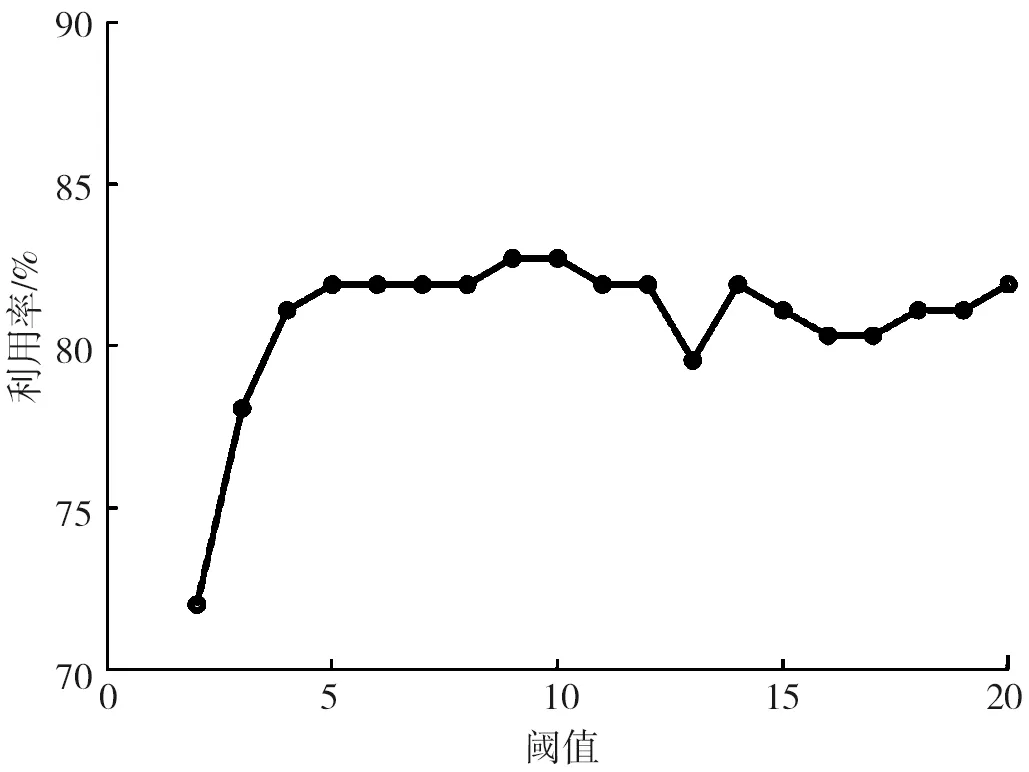
图7 dataA1中阈值和利用率的关系Fig.7 Relationship between threshold and utilization in dataA1

由图7可以看出，随着阈值的增加，板材的利用率也在逐渐提高，当阈值ε=10左右时，板材的利用率最高可达到82.71%。因此，对于数据集1，本文取ε=10，即对那些边长相等的物品数量≥10的分组利用第2节的操作来组合为条带，边长相等的物品数量小于10的个体归入类别3。

4.3 板材布局

对于2022 年“中国光谷·华为杯”研究生数学建模竞赛B 题中的dataA1、dataA2、dataA3、dataA4和dataA5这5个数据集，利用以上过程来执行排样优化，并选取禁忌搜索算法［13-14］进行对比，最终得到的结果见表1。

表1 排样优化在5个数据集上的结果对比Table 1 Results of layout optimization across five data sets compared

由于并不知道实际的最优板材数量，但可以计算最优板材数量的下界，即“最优板材数量下界”，它通过利用产品项的总面积和除以板材面积，并向上取整得到。由表1 可以看出，本文的方法在5个数据集上的板材利用率基本上都可保持在80%以上，并且高于禁忌搜索算法的结果。其中，对于dataA1，物品总面积为2.486 9×108，需要的板材数量为101 个，板材的利用率为82.71%。图8 给出了dataA1的第一个板材上的排样效果图。

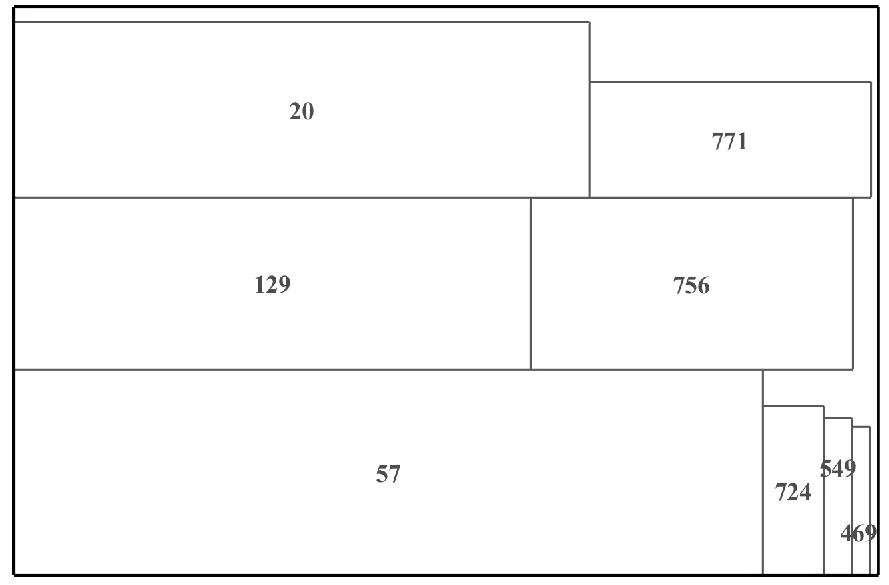
图8 dataA1中第一个板材上的产品排样Fig.8 Product layout on the first plate in dataA1

5 结论

针对多约束产品排样问题，提出一种两阶段遗传算法和贪心策略相结合的排样优化方法。该方法通过分析产品排样问题的特征，设计局部最优解码方案，采用两阶段遗传算法来实现产品和条带的最优布局，并针对产品余料和条带余料分别设计基于贪心策略的再利用方案。利用2022年研究生数学建模竞赛B题的5种数据集进行测试，通过模型对比和分析，验证了本研究模型的有效性。该模型的建立为有切割次数和切割限制的排样优化问题提供了一种新的求解方案。下一步的工作将针对多约束排样优化问题的特点建立集成学习模型，从而设计更为有效的邻域搜索策略，以进一步提升板材的利用率。