某物流车非独立前悬架K&C特性分析及优化
2023-10-22于国飞陈润发
刘 峙,于国飞,陈润发
(厦门理工学院机械与汽车工程学院,福建 厦门 361024)
现有的物流车多采用独立前悬架,导致制造和维护成本都较高。非独立悬架具有结构简单、成本低和维修方便等优点,但因其悬架特性较差影响到汽车的操纵稳定性。改善非独立前悬架特性对提升汽车的操纵稳定性和降低物流车的制造成本具有重要意义。
悬架K&C(kinematics &compliance)特性是影响车辆操纵稳定性的重要因素,改善悬架K&C 特性是提升操纵稳定性重要前提。陈云等[1]以某客车前空气悬架为研究对象,在充分考虑其他系统和外界条件对悬架计算结果的影响后,对悬架刚度、固有频率和侧倾刚度进行计算,将计算结果和试验结果对比,计算结果满足设计要求。高金良等[2]对麦弗逊悬架特性进行优化,利用切比雪夫多项式零点插值技术改进响应面模型,针对该模型采用双层嵌套的改进非支配排序遗传算法和粒子群算法进行多目标优化,改善了悬架特性。刘红领等[3]以扭转梁横梁开口方位角、横梁截面厚度、横梁垂向位置等参数为设计变量,利用ADAMS软件建立扭转梁悬架模型进行K&C 性能优化仿真分析。张翔等[4]以某轿车多连杆后悬架为研究对象,通过 ADAMS/Insight 和 Matlab 联合仿真,对硬点坐标和衬套进行灵敏度分析,采用 NSGA-II 算法对硬点坐标和衬套刚度进行多目标优化。张召振等[5]以响应曲面模型和遗传算法为优化手段,以车辆操纵稳定性和平顺性相关评价指标为目标函数,以车辆的钢板弹簧刚度、前横向稳定杆刚度和后横向稳定杆刚度为优化设计变量进行多目标优化,得到最优参数解来改善车辆操纵稳定性和平顺性。魏恒等[6]在汽车垂向运动和侧向运动之间的动力学耦合机制分析的基础上,建立多维耦合的独立悬架汽车摆振系统动力学模型。李志清等[7]针对空气悬架系统模糊PID 控制方法中参数选取存在局限性和难以选取的问题,利用遗传算法优秀的全局优化搜索能力和并行能力,提出了一种用遗传算法来优化模糊PID控制器参数的策略。综上所述,现有文献中大多数对独立悬架进行分析优化,而对非独立前悬架少有研究。为此,本文借助ADAMS 仿真平台对非独立悬架特性进行分析,在此基础上对悬架结构进行多目标优化设计,为非独立前悬架特性改进提供参考。
1 模型的建立
钢板弹簧既是悬架的弹性元件,又是悬架的导向机构,连接车轴和车架,传递各个方向的力和力矩,约束控制车轮的跳动轨迹,因此钢板弹簧的合理建模对悬架特性分析有至关重要的作用。
1.1 钢板弹簧模型的建立
变截面钢板弹簧的轮廓线包括梯形和抛物线型2类。每类中又包含根部、端部加厚,只有根部加厚和根部、端部都不加厚几种变型。抛物线型的优点是在抛物线区段内应力相等,材料利用率最高,是最为理想的类型,多用于中小型车辆[8]。本文选择抛物线型根部和端部都不加厚的钢板弹簧,钢板弹簧参数如表1所示。根据弹簧参数计算得到钢板弹簧的静刚度为253.75 N·mm-1。

表1 钢板弹簧参数Table 1 Parameters of leaf spring
1.2 钢板弹簧模型验证
使用ADAMS/Car的 Leafspring 模块建立柔体钢板弹簧模型,建立的钢板弹簧在弹簧叶片间产生接触力,模拟夹紧力矩和垂直载荷的变化造成的摩擦力,较好地模拟钢板弹簧实际的使用情况[9]。表2为变截面钢板弹簧的部分中心轮廓坐标及厚度。各参数设置后建立变截面钢板弹簧柔体模型,具体如图1所示。

图1 钢板弹簧柔体模型Fig.1 Soft body model of leaf spring

表2 变截面钢板弹簧部分中心线轮廓坐标及厚度Table 2 Partial centerline contour coordinates and thickness 单位:mm
为验证钢板弹簧柔体模型的准确性,将建立的钢板弹簧模型导入Adams/view 模块对其进行简化处理,在前卷耳和大地之间、吊耳和大地之间及吊耳和后卷耳之间3处分别施加旋转副约束,在中间无效片段处施加载荷F,得到如图2所示的钢板弹簧验证模型。
图2 钢板弹簧验证模型Fig.2 Verification model of leaf spring
将钢板弹簧柔体模型的理论静刚度和仿真静刚度进行对比,验证建立的钢板弹簧柔体模型的准确性。在钢板弹簧根部平直段处施加一个每秒增加2 000 N 的方向向上的载荷模拟静刚度工况,得到理论计算和仿真分析静刚度对比曲线如图3所示。由图3计算可知,仿真平均静刚度为234.67 N·mm-1。由于通过ADAMS/Car Leafspring 模块建模来模拟夹紧力矩和垂直载荷的变化造成的摩擦力,所以仿真静刚度并不是一个固定值,它和理论静刚度之间存在误差。仿真静刚度与理论静刚度相比,误差仅为7.5%,在合理误差范围之内,说明所建立的钢板弹簧模型是正确的,可用于进一步的研究。
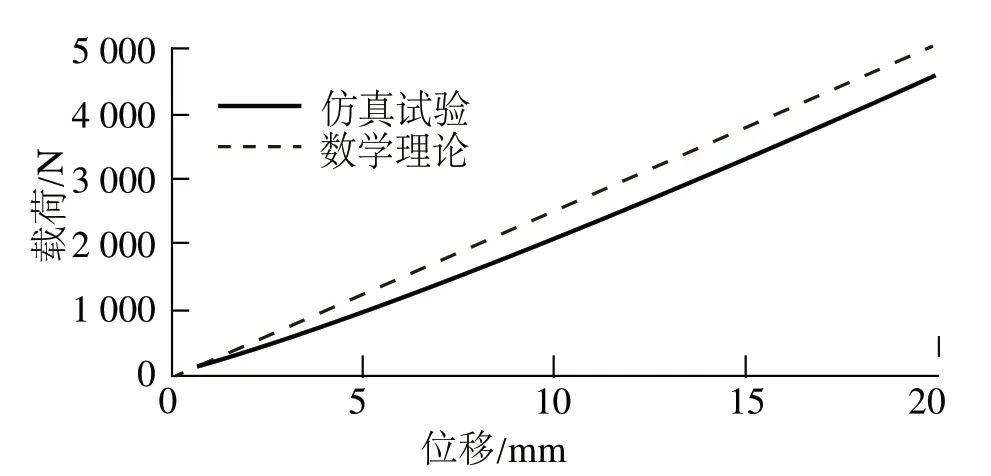
图3 理论计算和仿真分析静刚度对比曲线Fig.3 Static stiffness by calculation and simulation analysis compared
2 悬架特性分析
非独立前悬架主要结构为钢板弹簧总成、减振器、控制臂等。悬架关键硬点坐标汇总如表3 所示,搭建非独立前悬架试验台如图4所示。

图4 非独立前悬架试验台模型Fig.4 Testing model of dependent front suspension
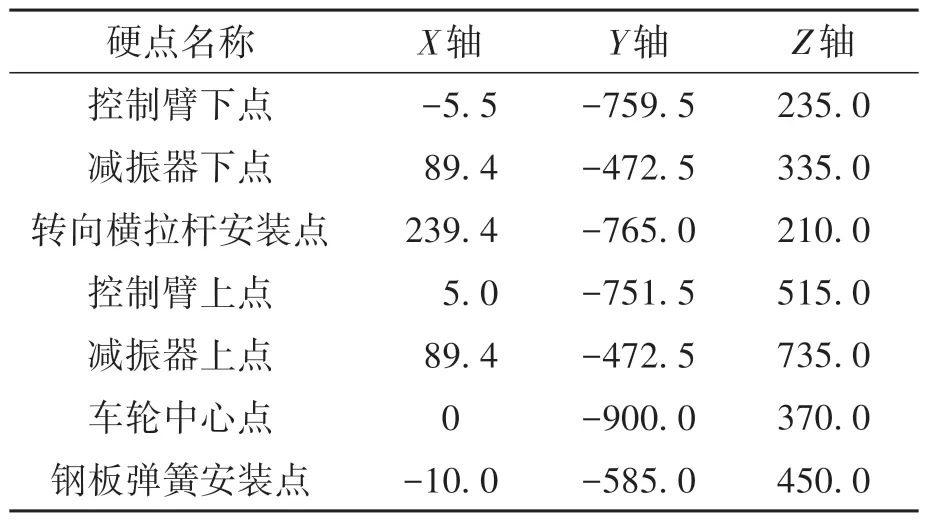
表3 非独立前悬架主要硬点坐标Table 3 Main hard point parameters of front suspension in mm
2.1 悬架K特性分析
在悬架设计中,悬架K特性的设计要求为车轮前束角范围变化量应控制在1°以内,而且随着车轮上跳,车轮前束角应该向零或者负前束方向变化,从而使车辆具有一定的不足转向特性,有效提高整车稳态转向特性。车轮外倾角范围变化量应控制在1°以内,随着轮胎上跳,车轮外倾角由正外倾向负外倾变化,与前束角变化相匹配[10]。车轮前束角仿真曲线如图5(a)所示,车轮外倾角仿真曲线如图5(b)所示。由图5(a)可知,在轮胎跳动量为-30~30 mm 过程中,车轮前束角变化范围为-0.967°~0.413°,变化范围较大,有待优化;由图5(b)可知,车轮外倾角变化范围为-0.214°~0.072°,满足设计要求。
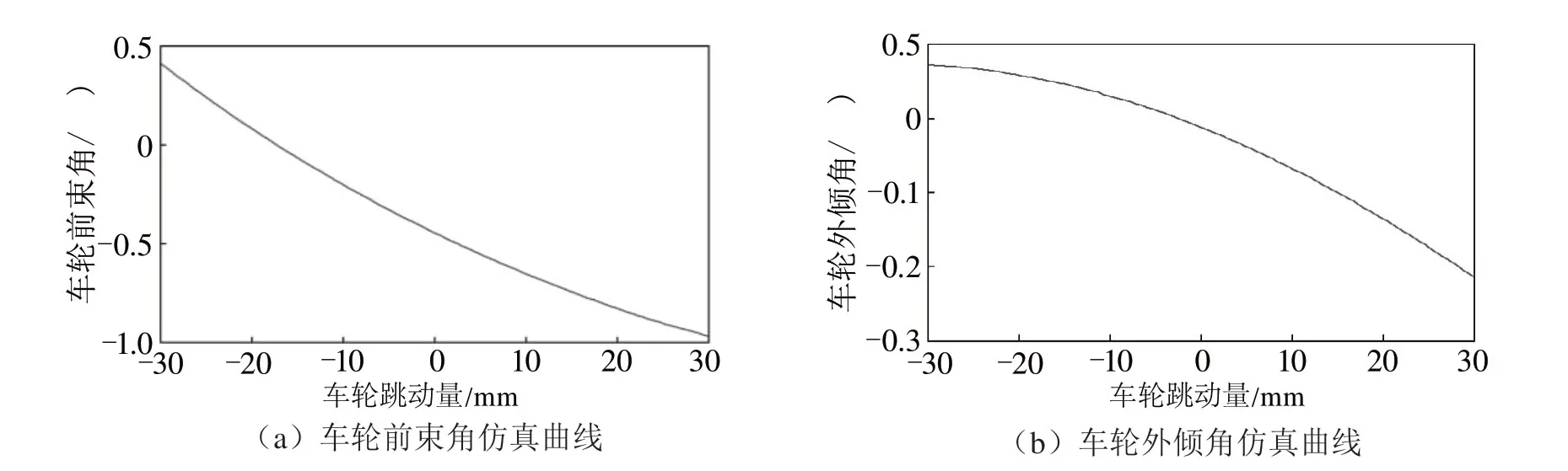
图5 K特性仿真曲线Fig.5 Simulated K characteristics
2.2 C特性分析
在车轮接地处从左到右施加一个-2 000~2 000 N 的力[11],左右车轮同向加载。设置完成后,执行仿真分析,车轮前束角、车轮外倾角仿真曲线分别如图6(a)和图6(b)所示。车轮前束角变化范围-0.068°~ 0.043°,车轮外倾角变化范围-0.000 4°~0.000 8°,变化范围很小,满足行业要求。
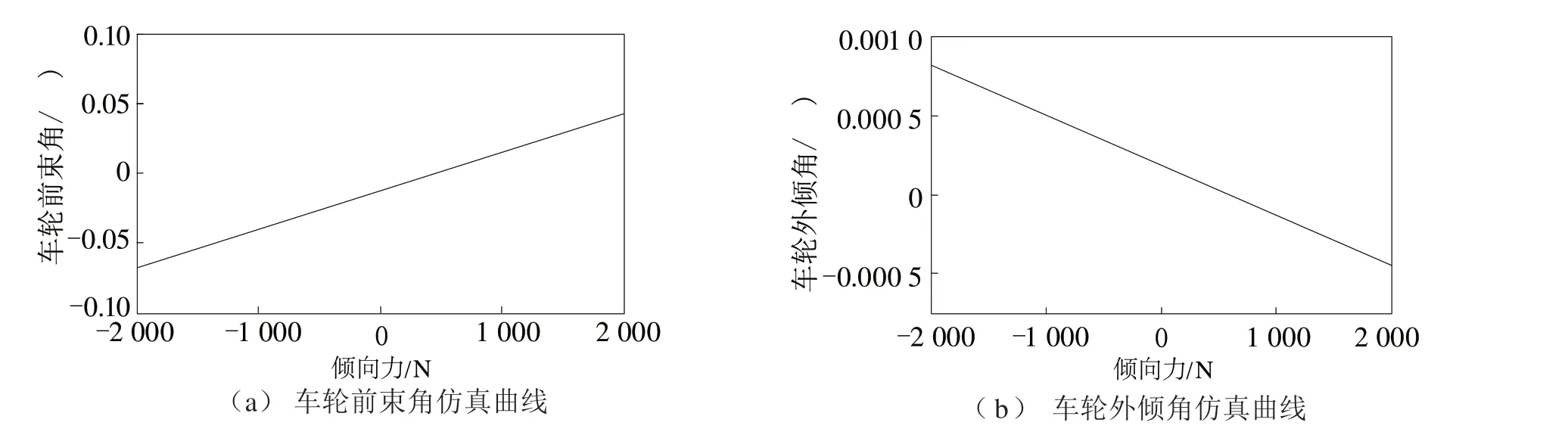
图6 C特性仿真曲线Fig.6 Simulated C characteristics
3 悬架的优化
在悬架K&C 特性分析中,K 特性分析前束角范围变化量为1.38°,变化范围偏大,需要进行优化。利用ADAMS/Insight 模块对悬架结构参数进行优化,其主要步骤为确定包含优化设计变量、目标函数、约束条件的优化设计模型。
3.1 确定优化设计变量
在优化过程中,如将所有硬点均作为优化设计变量则工作量很大,而且很多硬点位置对当前优化目标敏感度不高,从而导致优化效果不理想。因此在优化前须先对硬点进行敏感度分析,选择敏感度较高的硬点坐标作为优化变量。结合实际工程经验和尽可能少地改变悬架硬点坐标的原则,经过多次硬点组合敏感度分析,最终选择控制臂上硬点(upper_arm)、控制臂下硬点(lower_arm)、转向横拉杆硬点(tierod)、减振器上硬点(upper_shock)作为拟合变量。敏感度拟合指标[12]如表4 所示。表4 中R2表示优化数据的平方和与原始数据的平方和之比,变化范围0~1 之间,其值越大,表示拟合情况越好。通常小于R2,但当远小于R2时表明模型有些优化变量是多余的,其值越接近于1,表明拟合情况越好。P表示拟合过程中是否有其他可以计算项。R/V表明优化值与原始值之间的关系,其值越高越好,一般好的拟合其值应该大于10[13]。

表4 敏感度拟合指标Table 4 Sensitivity fitting indicators
车轮前束角的硬点敏感度分析结果如图7 所示。图7 中,控制臂下硬点x方向敏感度为41.97%,控制臂上硬点x方向敏感度为-37.54%,而其他硬点方向敏感度较低。综合考虑后,将控制臂下硬点x坐标、控制臂上硬点x坐标设为优化设计变量。
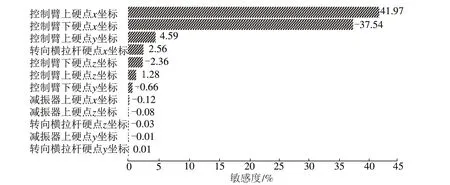
图7 硬点敏感度分析结果Fig.7 Sensitivity analysis results by hard point
3.2 优化模型的建立
将前悬架K特性仿真中的车轮前束角、车轮外倾角范围变化量的最小值作为优化目标函数,属于多目标优化设计问题。本文采用加权平方和法设计优化,建立优化模型为
式(1)中:σmax、ςmax分别为车轮外倾角、车轮前束角在迭代过程中最大绝对值;σ0、ς0分别为车轮外倾角、车轮前束角目标值;x1、x2分别为控制臂下硬点、控制臂上硬点x坐标。
选择响应面模型算法作为优化算法。响应面模型通过多项式函数拟合设计空间,具有能通过较少试验得到精确结果、可拟合复杂响应关系和实用性强等优点,其表达式为
经过多次迭代,计算得到悬架优化后的硬点坐标x1=-7.2 mm,x2=-3.3 mm。
3.3 试验验证
在相同环境中设计仿真试验,得到优化前后前束角和外倾角随车轮跳动量变化对比曲线如图8所示。由图8 可知,前束角范围变化量从1.38°降低到0.755°,降低45.2%,且满足轮胎上跳时前束角由正前束向负前束变化,外倾角的变化范围和变化趋势也在合理范围之内。结果表明前悬架特性优化达到预期目标。

图8 优化前后前束角和外倾角随车轮跳动量变化对比曲线Fig.8 Changes of toe angle and camber angle varying with runout before and after optimization
4 结论
本文利用ADMAS/Car 软件建立钢板弹簧式非独立悬架模型,并对悬架的K&C 特性进行分析。分析结果表明,在K 特性分析中,车轮外倾角在合理变化范围之内,但其前束角变化范围为-0.967°~0.413°,变化范围较大,需加以优化。为此,根据K 特性分析结果在ADAMS/Insight 中建立多目标优化设计模型,确定目标函数,分析悬架各硬点敏感度,根据敏感度分析结果,控制臂下硬点x方向敏感度为41.97%,控制臂上硬点x方向敏感度为-37.54%,二者选定为设计变量。优化结果显示,优化后前束角变化范围为-0.507°~0.248°,范围变化量降低45.2%,表明优化后悬架特性得到改善。研究为后续非独立前悬架物流车性能改善提供一定的参考。
