四心圆法形成椭圆的误差分析

王甲春，林煜凯，曾瑞江

（厦门理工学院土木工程与建筑学院，福建 厦门361024）

画法几何学椭圆的经典画法是四心圆法，它需要用直尺和圆规画一个给定长半轴和短半轴的近似椭圆，用4个相切的圆弧绘制椭圆。用圆弧代替椭圆弧的方法形成椭圆，至少可以追溯到16世纪文艺复兴时期，甚至可追溯到公元1世纪的罗马竞技场中椭圆建筑的建造［1］。四心圆法被认为是最早手绘椭圆的方法，至今它仍在椭圆的制作中发挥着重要的作用。计算机时代工程图学要利用计算思维与图形思维相结合来解决工程问题［2］，虽然四心圆法绘制椭圆的历史悠久，但是针对此方法的计算分析才是近些年来开展的工作。闫培泽［3］研究了用数值四心圆法绘制椭圆的误差，得出短长轴比为0.24 附近时绝对误差值最大，但是没有揭示误差的分布规律。文献［4-5］讨论了四心圆法绘制椭圆的法向误差的变化规律，唐立波［6］给出了四心圆法绘制椭圆法向误差的三角函数表达式，周亚辉等［7］研究利用八心圆法来降低四心圆法的误差，但是这两种方法过于复杂。在建筑建造的过程中，椭圆形的混凝土建筑物、构筑物模板的支撑和安装需要明确绝对误差和相对误差，用以确定是否需要调整。因此，本文全面分析四心圆法形成椭圆的绝对误差和相对误差的变化规律，并利用CAD 三维表示四心圆法绘制椭圆和椭圆的相对位置关系，明确四心圆法形成椭圆误差的整体变化规律，计算出误差的极值点，便于四心圆法在建筑工程中的应用。

1 椭圆的形成

画法几何中四心圆法绘制椭圆（见图1），方法简单，用尺规能够完成，手工绘制方便，用四段圆弧来代替椭圆也有利于建造的实施。设椭圆的长轴为2a，短轴为2b，则其标准方程为

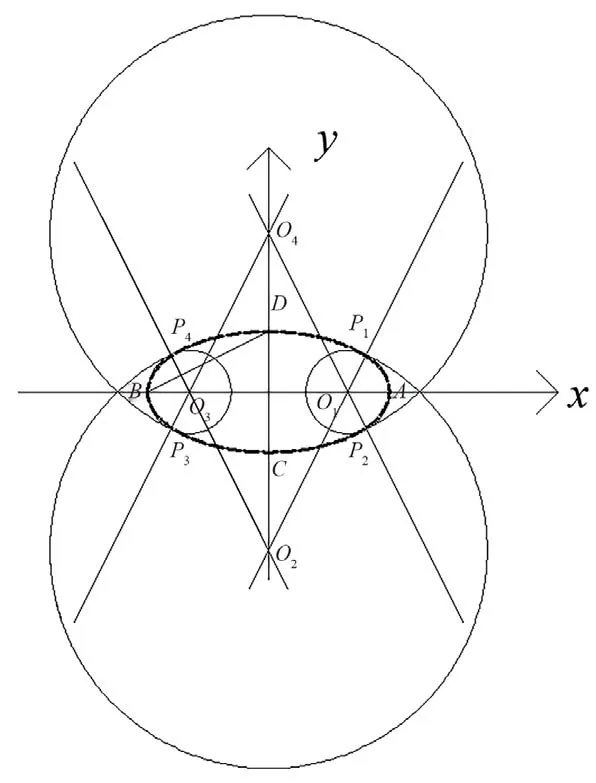
图1 四心圆法绘制椭圆Fig.1 Drawing ellipse by four-center method

圆2的方程为：

2 误差分析

2.1 误差的表达

由图2可见，除了椭圆端点A外，第一象限圆1的圆弧在椭圆弧外侧。由图3可见，第一象限圆2的圆弧与椭圆弧有一个交点M，DM段椭圆弧在圆弧的外侧，MP1段圆弧在椭圆弧的外侧，端点D是重合点，椭圆与圆2的交点M坐标［10］为。

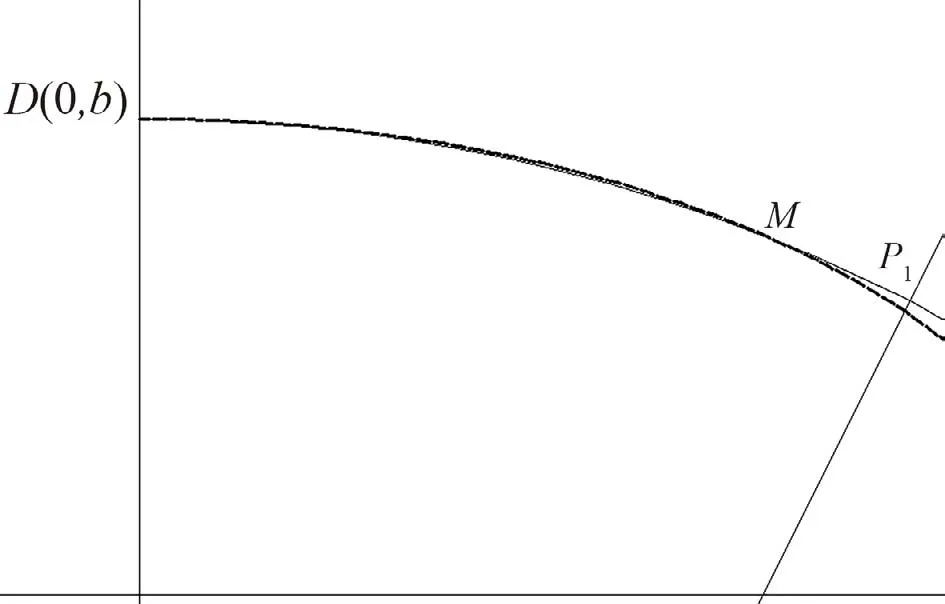
图3 第一象限圆2的圆弧与椭圆弧Fig.3 Arc and elliptical arc of the first quadrant circle 2

第一象限圆弧与椭圆弧的误差分析，两段圆弧的方程变形为

令绝对误差f为

由图4可见，绝对误差f在圆2段随着x值的增加而增加，属于正偏差，达到最大值后下降到负偏差，存在一个极大值点；绝对误差f在圆1 段是负偏差，存在一个极小值点，整个绝对误差曲线呈“钩状”。另外，由图4的两条曲线来看，b值固定，a值增大，绝对误差f的绝对值增加。

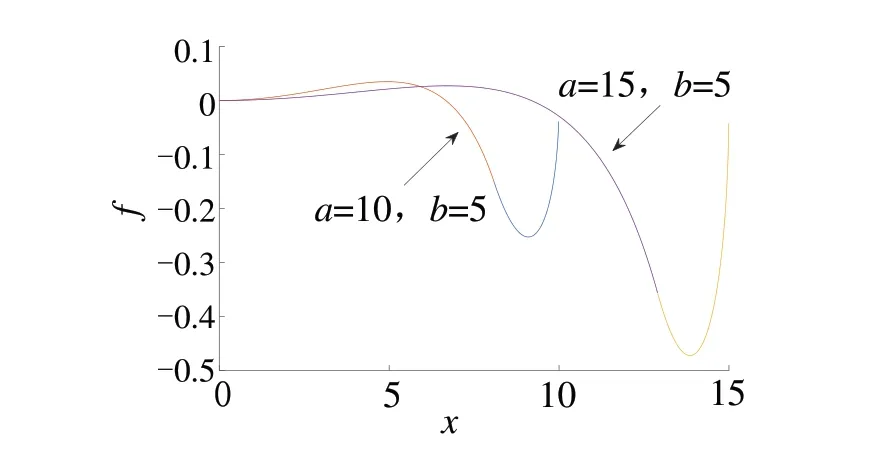
图4 绝对误差随x值的变化Fig.4 Absolute error varying with x value

相对误差g为：

由图5可见，相对误差在长轴端点附近快速增加，这主要是由于长轴端点附近椭圆y值接近于0，因此，相对误差快速增加。

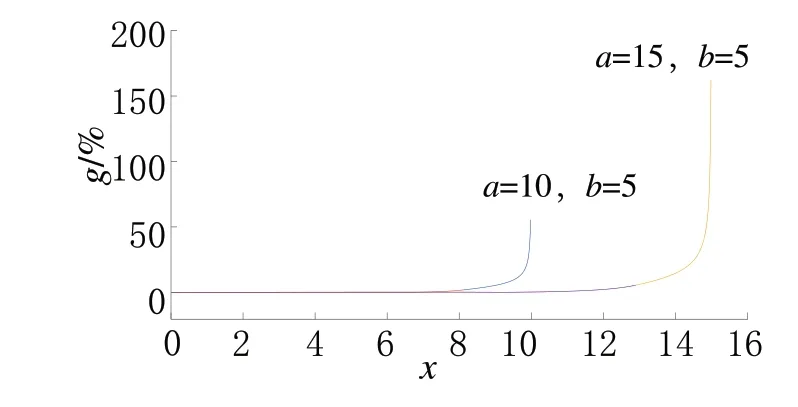
图5 相对误差随x值的变化Fig.5 Relative error varying with x value

2.2 结果分析

分析椭圆尺寸对绝对误差f的影响。令，分别比较两个圆的切点附近的绝对误差f的变化规律，结果见图6。计算的点的位置位于切点P1附近，可以看出，k值增加，绝对误差f值的绝对值越大，也就是椭圆越扁，绝对误差越大。

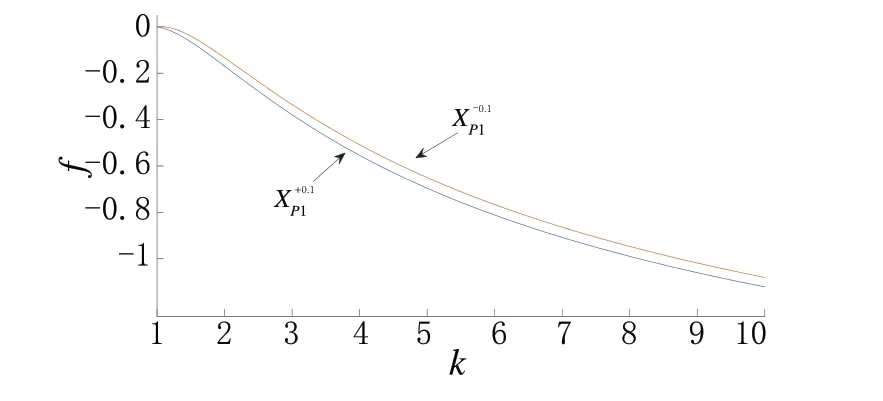
图6 绝对误差随k值的变化(b=5)Fig.6 Absolute error varying with k value (b=5)

绝对误差曲线的极值点，先求偏导数。即

式（6）是一元四次方程，利用Matlab 求解，但是根的通式太繁琐。通过数值解得到验证，当a=10、b=5时，解出符合要求的根x2=9.095 4；当a=15、b=5时，解出符合要求的根x′2=13.856 3，由图4可见，这两个根是正确的。

应用CAD 软件以四心圆法绘制圆弧形成的椭圆和相同长短轴的椭圆为边界旋转形成椭球体，如图7 所示，蓝色是四心圆法绘制部分，灰色是椭圆部分。由图7可以看出两个椭球体的差别，长轴附近是圆包裹椭圆，也就是四心圆法绘制的椭圆大于真实的椭圆，在短轴附近椭圆与圆非常接近。

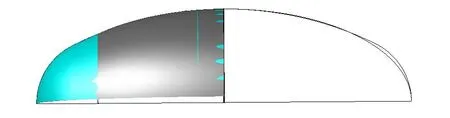
图7 四心圆法绘制椭圆的三维表示Fig.7 Three dimensional representation by four-center method

3 结论

通过对四心圆法形成椭圆的绝对误差和相对误差的分析，得到绝对误差的2个极值点，其中负偏差的极值点是四次方程的根；椭圆的长轴和短轴的数值确定后，可以计算出极值点的位置和误差大小；相对误差在长轴端点附近最大。利用CAD 三维绘图，可表达出椭圆误差的分布三维表示，在椭圆长轴的两端误差最大。