一种改进的线性变换与多尺度位置编码方法

周 伟

（厦门理工学院计算机与信息工程学院，福建 厦门 361024）

近年来，手写公式的识别逐渐成为了一个热门的研究内容，它在自动阅卷、在线教育、文档识别、公式录入等领域具有很强的应用需求。目前，手写公式的识别研究还处于初期阶段，局部歧义、手写风格迥异、结构复杂等问题仍未得以较好解决。在手写场景下，很多字符仅从形态上难以准确区分，比如手写的英文“b”和数字“6”、字母“x”和乘号等局部歧义和手写风格问题，这都需要结合上下文来推断字符的概率［1］。另外，公式中常常包含一些结构复杂的符号如∑、∏、∫、log 等，符号之间的位置关系有上下、左右、右上、右下、半包围等，既要识别符号本身，又要识别与其他符号之间的关系，这是公式识别的难点所在。

在公式识别研究领域，早期的方法是将其先切分再识别［2-3］，但该方法容易切分错误，影响识别结果，且切分之后的符号识别未能考虑上下文信息。Sutskever等［4］提出序列到序列的方法，之后，研究人员开始使用编码器-解码器的无切分方法［5］，该方法将公式图片在编码器中转换为一个中间向量，中间向量又在解码器中转换为输出序列，这成为公式识别领域的一个热门研究。Zhang等［6］针对书写风格迥异的问题，添加了空间和时间注意力机制，融合多种不同模态的信息提升效果，该系统在线识别在CROHME2014、CROHME2016 的识别率分别为61.16%、57.02%。Deng 等［7］提出了由粗到细的注意力机制，用于识别印刷体和手写公式，在Im2latex-100k、CROHME2014 的识别率分别为79.88%、38.74%。Zhang 等［8］提出了多尺度空间注意力机制，解决由字符尺寸差异较大带来的字符丢失问题，该方法在CROHME2014、CROHME 2016 的识别率分别为52.8%、50.1%，而且，该方法能够有效处理一些尺寸较小的符号识别，比如小数点或上标等。Nguyen 等［9］提出一种空间分类特征的聚类方法，根据手写符号大小不同尺寸如下标或上标符号等，从多个尺度中提取输入图像的特征，并度量图像之间的空间距离。Zhang等［10］将基于树结构的双向长短时记忆方法用于在线公式识别中，提取公式的二维结构。张建树［11］也使用树结构进行离线手写公式识别，在CROHME14、CROHME16、CROHME19的识别率分别为49.1%、48.5%、51.4%。Wu 等［12］提出了一种简称PAL-v2 的端到端模型，采用新颖的对抗学方法来学习语义不变特征，以处理手写公式书写风格和格式的多样性问题，该模型在CROHME14、CROHME16 的识别率分别为48.88%、49.61%。以上模型在手写公式识别领域均取得不错的效果，除了树结构方法是专门处理位置的之外，其他研究内容都主要放在空间注意力、字符尺寸、书写风格等内容上，与位置编码方法相关的手写公式识别的研究成果较少，而它又是深度学习中处理结构关系和逻辑关系的有效方法。

关于深度学习中位置编码的相关研究，Vaswani等［13］提出一种新颖的位置编码，即正余弦函数交替的位置编码，将词在句子中所处的位置映射成向量，补充到特征向量中，并通过线性变换和点积学习单词之间的距离和相对位置，被证明是一种有效的位置编码方法。之后，位置编码在自然语言领域不断演变出新的方法，如：Chu等［14］提出条件位置编码和位置编码视觉转换器，根据输入序列的大小而变化，处理各种尺寸的图像，并可以保持平移不变性；Liu 等［15］提出FLOATER 绝对位置编码，解决长度限制问题，提升长度未知的泛化能力；Dai等［16］在Transformer-XL 模型中采用相对位置编码替换绝对位置编码，解决长序列的建模问题，它通过每个层注意力处理了词和词之间的距离差。在自然语言处理领域，位置编码方法均取得较好效果。在手写图像识别上，Sabour 等［17］曾提出胶囊网络采用输入向量与权重矩阵相乘方法，编码低级和高级特征之间的空间关系，该方法比较重视卷积网络中特征之间位置关系，虽然能处理局部与整体之间的关系，在手写数字数据集上表现突出，但是网络参数（标量）均替换为向量，比卷积网络运算量大，泛化能力差。因此，本文提出一种改进的位置编码方法，利用三角函数线性变换性质，提取符号的绝对位置和符号之间的相对位置，同时结合多尺度方法，在水平、垂直方向分别进行不同尺度的比例伸缩，以增加符号之间的间距，并分别突出水平、垂直方向的结构关系，从而提取更细微的符号和符号之间的位置关系。

1 位置编码方法

公式符号之间包含重要且复杂的位置关系，除了先后之外，还包含上下标、包围、嵌套等关系。首先，由于卷积网络存在难以建模位置（时序信息）的缺陷；其次，循环神经网络在隐藏层每个时间点接收上一个时间点的隐藏状态，能够建立前后时序的关系，但是无法处理公式的复杂结构关系，如上下、包围等。所以，在编码器的特征提取过程中，需要单独保存位置信息，否则在全连接层进行特征整合之后，就会丢失符号之间的位置关系，如符号a2可能被误识别为a2、a2、2a等结构错误，甚至符号错误。

位置编码的表示方式有多种，三角函数被证明是一种有效的表示方法，它具有线性变换性质。如位置p和p+Δb，通过公式sin（p+Δb）=sin（p）cos（Δb）+cos（p）sin（Δb）和cos（p+Δb）=cos（p）cos（Δb）-sin（p）sin（Δb），位置p+Δb可以通过位置p和Δb表示或者变换得到，也就可以学习它们的相对位置关系。

在Transformer 文本序列问题中，词在序列中的位置是一个数字，在二维公式图像中，位置是一个坐标（x，y）。设特征向量的尺寸为（h，w），x∈［0，h），y∈［0，w），dm表示时间序列数量，它的值与通道数量相同。在某个时刻i，i∈［1，dm］，生成2个位置函数信号sin（）、cos（）分别编码奇偶时刻的位置。这些正弦、余弦信号连接成一个位置向量P2，这个向量的第i个时刻位置（x，y）的编码是P2（x，y，i），计算公式为

假设特性向量尺寸（h’，w’）的值为（14，14），不同坐标位置编码P2（x）用正弦或余弦函数交替编码，而且不同的时刻i（即维度）可以采用不同的三角函数的相位和频率，不同时刻i的x位置编码函数具体如图1所示。由图1可见，这正好符合位置编码的要求，即各个维度周期不一样，而且同一维度内部的值既要有差距，又不能差距太大（在长序列中泛化能力差）。

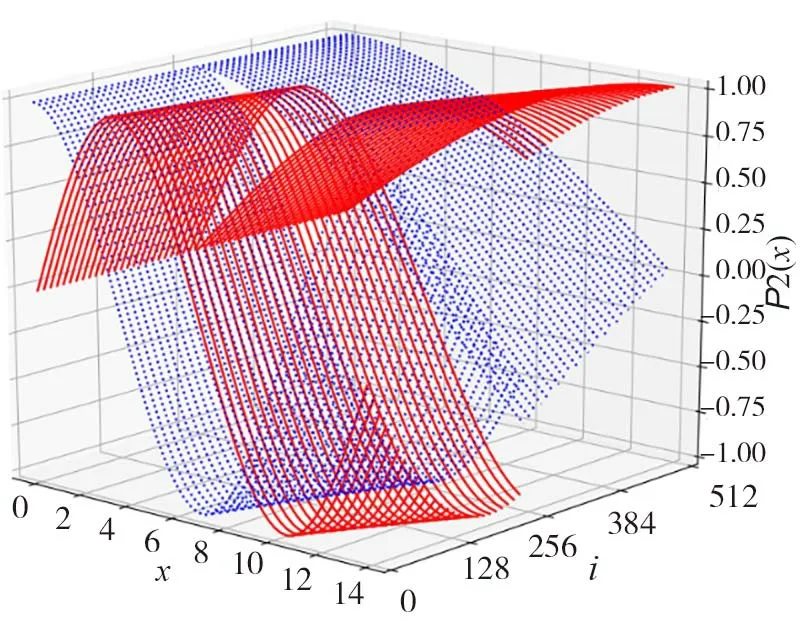
图1 不同时刻i的x位置编码函数图Fig.1 Function graph of position x at different time i

位置信息x与y是分开存储的，位置的向量维度dm，高度h’，宽度w’，dm的值为512，那么位置x存储在［0，256）的维度，位置y在［256，512）的维度，时刻i=1位置向量分别是［1，14，1，256］和［1，1，14，256］，具体如图2 所示。接着，经过每一个时刻i之后，填充成完整的位置向量，发现位置向量与特征向量尺寸是一样的，具体如图3 示。位置向量与特征向量结合的方法有多种，本文把2个向量相加，拼接起来作为一个新向量，即包含特征和位置的中间向量。

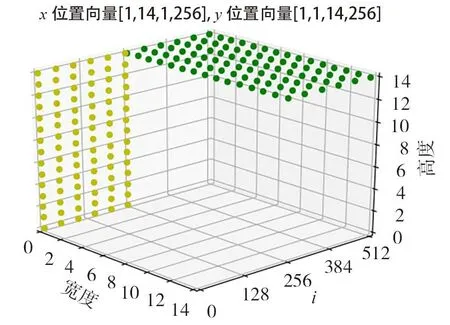
图2 初始时刻的位置向量图Fig.2 Initial position vector

在训练中，以不同的尺度比例进行拉伸或缩放位置特征，在更大尺度下提取放大的特征。在尺度不变的情况下，对x坐标以m∶1 尺度变换，可增加符号之间的横向间距，更好区分开符号。同样，y坐标以n∶1 尺度伸缩，则从纵向上增加间距，更明显突出上下结构关系。在x坐标和y坐标上分别进行的伸缩变换情况如图4所示。这样能让1张图片按不同时刻生成2张伸缩图片，而m和n的值要满足m＞1 和n＞1（本文设m、n的测试值为3 和2）。公式（1）加入位置尺度m∶1 之后，在时刻（维度）i∈［1，］的位置x的编码函数如式（2）和式（3）所示：

图4 在x坐标和y坐标上分别进行伸缩变换示意图Fig.4 Graph of makes different scale transformation on x coordinate and y coordinate respectively

加入尺度m∶1伸缩之后，奇偶时刻正余弦函数交替的编码式子仍然满足线性变换，公式P2（p+Δb，2i）=sin（mp+mΔb）=sin（mp）cos（mΔb）+cos（mp）sin（mΔb）、P2（p+Δb，2i+1）=cos（mp+mΔb）=cos（mp）cos（mΔb）-sin（mp）sin（mΔb）仍然成立。由于常量Δb是已知的，设u=sin（mΔb），v=cos（mΔb），那么替换之后，P2（p+Δb，2i）=P2（p，2i）u+P2（p，2i+1）v，P2（p+Δb，2i+1）=P2（p，2i+1）u-P2（p，2i）v，矩阵变换表示形式为

另外，位置向量的值相乘也能得到位置之间的距离信息，计算公式为P2（p+Δb）P2（p）=sin（mp+mΔb）sin（mp）+cos（mp+mΔb）cos（mp）=cos（-mΔb）=v，距离值v是已知常量，能代表两者的距离（非真实距离）。

2 离线手写公式识别模型

为了验证以上位置编码方法，本文设计一个离线手写公式识别模型，包括密集卷积网络、位置编码、循环神经网络和注意力机制等主要模块。模型结构如图5所示。

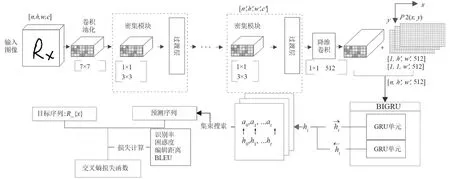
图5 离线手写公式识别模型结构图Fig.5 Recognition model of offline handwritten mathematical expression

卷积网络在图像特征提取上具有明显的优势，并且密集卷积网络引入跳跃式连接网络，打破了n-1 层输出只能作为n层的输入的习惯，输出可以直接跨过多层作为后面某一层的输入，它的特征共享和任意层互联的特性，解决了深层网络在训练过程中梯度消散而难以优化的问题，而且减少了网络的参数和计算量。本文的卷积网络结构如图5所示，它包括多个密集块和过渡层，由于密集块的每一层输入是前面所有层的输出，第t层的输入是［x0，x1，…，xt-1］，第t层的输出是xt，k表示每个密集块中每层输出的特征图个数，每经过一个层，下一层的特征维度就会增长k，k值越大意味着在网络中流通的信息也越大，网络的能力也越强，同时网络的尺寸和计算量也会变大［18］。参考DenseNet-121 网络结构，本文输入图像尺寸［n，h，w，c］，其中：h为高度；w为宽度；c为通道数。首先，图像经过64个7×7卷积核与池化层，其次是3个密集块，密集块分别包括｛n1=6，n2=12，n3=24｝个的1×1卷积核和3×3卷积核，设增长率k的值为32，特征图数量为c’为64，经过第1个密集块和过渡层之后，c’加上n1c×k再除2，即(64+6 × 32)/2=128。以此类推，经过3 个密集块和过渡层之后，特征图数c’为512，即特征向量尺寸为［n，h’，w’，512］，并嵌入同样尺寸的位置向量之后，即得到最终的编码器输出。

模型的另一个模块是典型的双向门控循环单元（bi-directional gate recurrent unit，BiGRU），它是一种特殊循环神经网络（recurrent neural network，RNN），是处理序列问题的有效方法，并且解决了RNN的梯度爆炸、梯度消失、短时记忆的问题，并且GRU 弥补了RNN 短时记忆的不足，适合处理长度复杂的公式识别问题。GRU的参数为

只有更新门rt和重置门zt2 个门参数，重置门有助于捕捉短期的依赖关系，而更新门有助于捕捉长期的依赖关系。减少门则减少了参数，两个门的权重参数为Wr和Wz，参数和计算量相比LSTM 少，训练更容易收敛。

接着，把每一个前向隐藏状态和后向隐藏状态拼接为隐藏状态ht，如

ht再加入到输入和输出中间的隐含层，这层可以学习到每个符号的上下文特征。因为数学公式的符号之间具有时序关系和上下文关系，每个特征在转换为符号时都要考虑前后上下文的关系，只考虑从前往后的信息序列是不够的。有些数学公式需要参考前面的符号才能识别，同样，有些前面的符号参考后面的符号加以识别，比如手写的‘）’与‘1’，它们形状相似，需要根据前面是否有符号‘（’加以判断。

为了防止序列关键信息丢失，添加注意力机制是一种常用方法，尤其是处理公式比较长的任务，它在不同的时间使用不同的隐藏状态，即权重系数Wt，给关键的符号区域分配更大的权重系数，减少关健信息丢失，通过注意力机制计算每个时刻隐藏状态对应的权重at，其计算公式为

式（7）中：Wt表示ht的权重系数；ut表示注意力层的第t个时刻隐藏状态；uw表示随机初始化的注意力矩阵；at为第t个时刻隐藏状态对应的权重。ht输入到注意力层，得到注意力层t时刻的隐藏状态ut，再进行归一化计算注意力的权重概率分布at，带权求和得到上下文特征向量st=∑atht，由st、隐藏层状态ut，以及前一时刻预测符号yt-1预测目标符号yt。

3 实验结果与分析

本文采用的评价指标除了识别率之外，还有3 个机器翻译的评价指标，即：BLEU（biLingual evaluation understudy）［19］、困惑度、编辑距离。公式是由多个符号按照一定结构顺序组合的序列，它的识别是序列到序列的过程，这与机器翻译（序列到序列）过程相似。所以，训练和评价模型不能仅仅通过比对整个目标序列是否正确，还需要计算预测值与目标值的相似程度。

BLEU是一种机器翻译中常用的自动评价指标算法，计算预测与参考之间的相似程度，它是一个比较候选文本与其他一个或多个参考文本的评价分数。除此之外，BLEU也用于其他语言生成、图片标题生成、文本摘要、语音识别等。通过对候选文本与参考文本中的相匹配的n元组进行计数，当n的值为4时，即BLEU-4。BLEU-4分数范围在0～1，越接近于1，则效果越好。困惑度是一种交叉熵的指数形式，它和交叉熵都可以用来评价模型的好坏。困惑度越小，准确率就会越高，也被认为是平均分支系数，即预测下一个符号有多少种选择分支，选择分支越少，模型也越准确。对于模型M=P（wi|wi-N+1…wi-1），它的困惑度Perplexity（W）公式可定义为交叉熵的指数形式，即

式（8）中：W代表数学公式；N是公式长度；H（W）是交叉熵；P（wi）是符号的概率分布。

编辑距离是自然语言处理中度量序列相似程度的指标之一，假设两个序列为A、B，序列A［0，i］与序列B［0，j］的编辑距离是由它们之间所需要的最少单字符编辑操作的次数决定的，其计算公式为

式（9）中：i，j表示序列中的位置，i∈（0，|A|），j∈（0，|B|）。

本文实验使用了CROHME 2014 和CROHME 2016 两个数据集，它们是在线手写公式数据集，经过点数据可视化转化为离线手写公式图片。CROHME 2014包含训练集8 836个公式、测试集986个公式、101 种符号［20］；CROHME 2016 是以CROHME2014 测试集为验证集，另外测试集包括1 147 个公式［21］。本文在CROHME2014、CROHME2016 数据集的实验数据与其他文献的对比结果如表1 所示。由表1 可见，本文的识别率比DenseWAP-TD、PAL-v2 提升约1%，含1 个字符错误的识别率与DenseWAP-TD、PAL-v2接近，含2个字符错误的识别率比DenseWAP-TD、PAL-v2平均提高1%～2%。另外，根据常见结构符号（如符号∑、∫等）预测值与目标值比对结果统计，本文的结构识别率分别为69.2%、68.9%，超过其他模型数据0.6%以上。

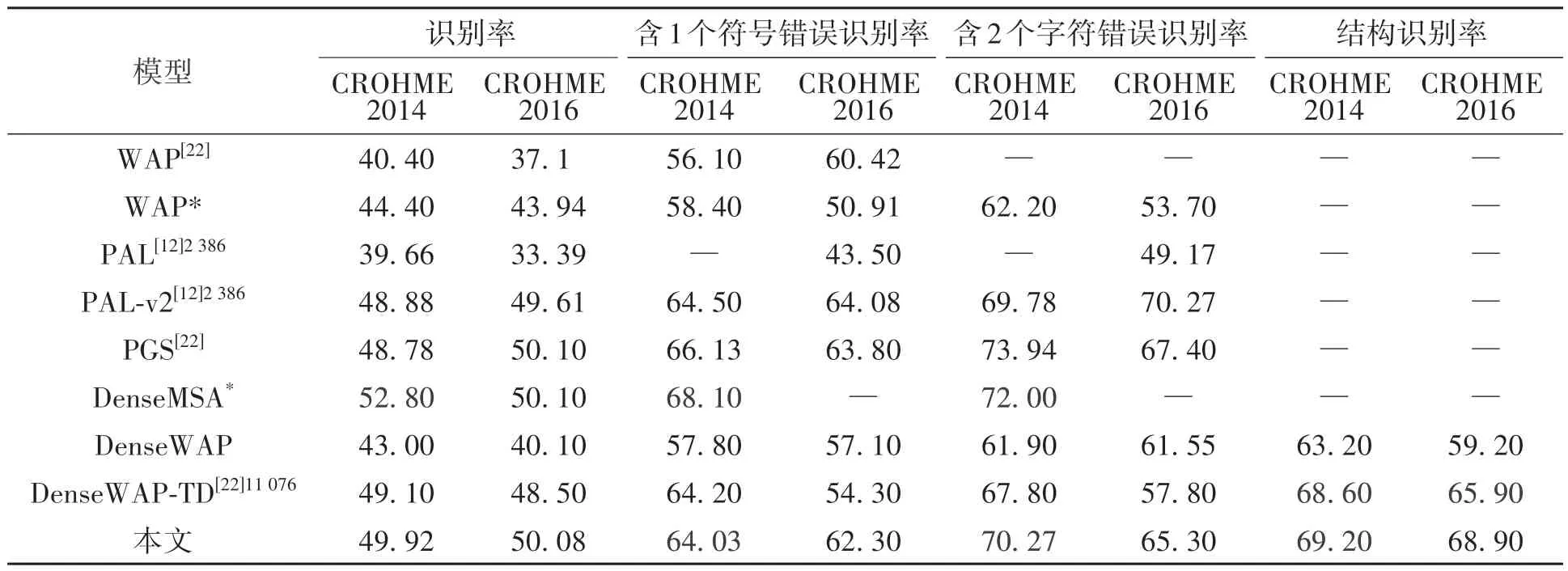
表1 不同模型在CROHME 2014和CROHME 2016 测试集上的结果对比Table 1 Results of different models on the CROHME 2014 and CROHME 2016 test sets compared 单位：%

模型训练过程的指标变化如图6 所示，可见，开始训练之后，识别率很快突破0，并以较快的速度提升，约20 批次之后提升速度缓慢，并逐渐收敛，第120 批次时的识别率50.08%，迭代次数少且收敛快。困惑度的值如图6（b）所示，它的值从10 左右开始快速减少，并逐渐收敛于1.66（第120 批次），它的理想值是1，即只有1 个可选的预测分支。图6（c）和图6（d）分别是BLEU-4、编辑距离值的曲线图，在1～20 批次之间，它们的值先增加，有一个短暂的下降之后，再快速增加，增加的幅度从快到慢，并逐渐收敛于0.78和83.2，与识别率曲线图的变化规律相似。其中，BLEU-4值越高，预测序列与目标序列的相识程度越高，预测越正确。编辑距离值越大，表示序列之间距离越大，即模型对不同序列认识区分越清楚。优化的位置编码方法与普通坐标编码分别进行训练之后，3个评价指标变化曲线分别如图6的细线和粗线所示，可见，虽然两者模型训练都可以收敛，但是，前者的各个指标曲线收敛比较稳定，困惑度指标也比后者明显降低约1，BLEU-4、编辑距离和识别率分别提高约0.15、16和10%。

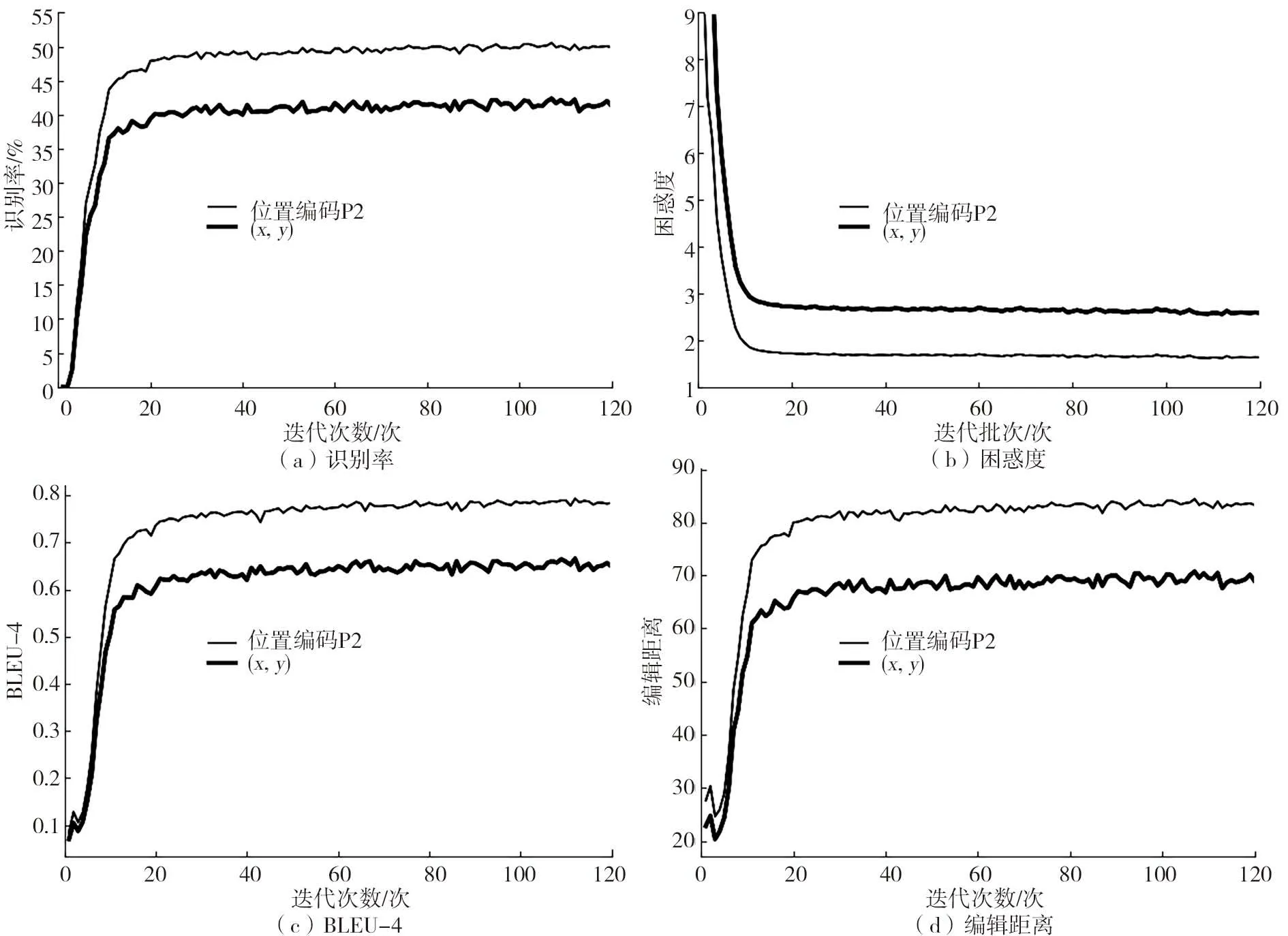
图6 在CROHME 2016测试集上的评价指标曲线图Fig.6 Evaluation results on CROHME 2016 test set

图7 是网络训练的几个关键时刻的可视化过程。由图7 可知，每一张图片灰色背景区域是注意力权重的可视化效果，区域的注意力权重越大，显示的灰色就越暗，图片上方是对应的位置区域的目标序列。

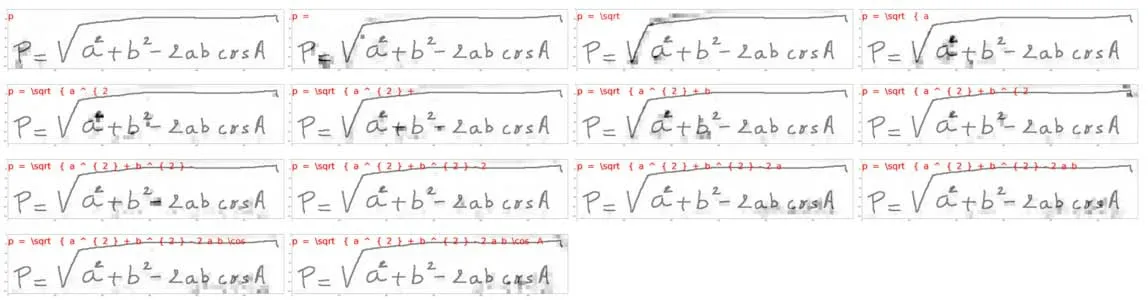
图7 图像生成目标序列的各个时刻截图Fig.7 Screenshots of attention at various moments when the image is converted into a sequence of text

除了识别率和评价指标之外，还需要进一步对预测序列与目标序列比对，并统计结构识别率、识别错误的字符数等。首先，关注识别错误的公式和符号，例如：33.5与335、h与k、a与α（alpha）、θ与e、N’与N、γ（gamma）与r、1 与i、log 与109、q与9、5 与S、n与h、n与π 等，但是以上错误并非必然，与手写风格关系大，尤其是手写比较潦草情况。其次，通过比对预测序列与目标序列的结构部分，分析模型识别公式结构的效果。

输入图像1：

输出序列1：sqrt ｛1+sqrt｛2+sqrt｛3+sqrt｛4｝｝｝｝

输入图像2：

输出序列2：a^ ｛b^ ｛c^ ｛d｝｝｝。能够识别到4 层的根号和3 次指数的公式复杂情况的结构。这2 个公式的结构比较深，难度已经非常高，本文加入位置编码之后，可以有效保存和传递符号之间的位置关系。但是，一些更复杂的符号结构仍存在识别错误，一般与2个以上的字母或者数字有结构关系，如极限符号lim、累加符号∑等。

4 结论

本文先引用正余弦函数交替的编码方法，在水平和垂直方向分别进行多尺度伸缩变换，并通过公式推导证明多尺度伸缩之后仍满足线性变换性质，编码之后的位置向量之间也能通过运算得到它们的距离，位置编码方法理论可行。然后，设计一个包含该位置编码方法的验证模型。验证实验显示，模型训练速度快，识别率很快突破0，训练约20批次开始逐渐收敛，约120批次之后稳定收敛，训练收敛快且稳定；在CROHME 2014 和CROHME 2016 的测试集上的识别率分别达到49.92%和50.08%，结构识别率分别达到69.2%和68.9%。另外，BLEU-4、困惑度和编辑距离等评价指标的值比较合理，且比普通坐标编码效果更好。证明了本文提出的位置编码的方法具有较好的可行性。未来仍需解决多尺度的参数优化的问题，引入和对比其他优秀的深度学习位置编码方法，进一步提高评价指标和识别率。