“说数学”在教学中的应用研究

牟庆生

摘要：数学是思维的体操，将数学思维过程用语言表达出来，有助于教师了解学生的动态，及时调整教学方向，实现教学相长.本文中以“函数的零点”教学为例，具体阐述如何选择“说”的内容，并提出“说”的执行方法.说开放话题，制造认知冲突；议议新问题，拟定解决方案；辨析新材料，验证解题方案；练典型例题，培养表述能力；评教学反馈，增强解题信心.

关键词：说数学；认知；材料

说数学是指学习者用口头表达的方式阐述自己对数学问题的认识、解题思路、思想方法与情感体会等的过程，一般可概括为：说知识、说过程、说异见、说体会.说数学是数学交流的基本形式，能让学生在表达中获得良好的交流能力，为数学核心素养的形成奠定基础.鉴于此，笔者以“函数的零点”教学为例，具体谈谈如何将“说数学”应用于实际教学中.

1 选择说的内容

学生认知发展的过程并不一定与教学过程相符合，其认知常常随着最近发展区的发展而发展.因此，在说数学的内容选择上，应契合学生的认知经验，只有着眼于学生认知的生长点，才能让说数学起到真正的教学作用.教师应精心设计教学过程，为学生搭建“说”的平台，并积极配合学生的“说”，让师生、生生之间通过对话的方式，完成教学任务，实现教学相长.

“函数的零点”教学是在函数概念的基础上进行的，可利用函数的性质、图象等解决方程问题，将函数的零点和方程的根融合在一起进行思考、分析.但在数形结合的对应上，学生常会出现偏差，有时因过分倚重一方面，导致其他因素被弱化，所捕捉到的信息不全，出现图形不准确或数据偏差等问题；也有学生因等价转化不合理，导致思维出现混乱等情况.

事实证明，解题不仅需要严谨的逻辑思维能力，还要有良好的直觉思维，而用语言表达则是训练学生直觉思维的良好方法.

綜上分析，笔者认为本节课的教学，训练学生的“说数学”能力可选取以下内容：①回顾零点的概念与判定方法；②排查教学活动过程中产生的问题，根据问题拟定解决方案；③课前自测，验证拟定的方案是否有效，提升学生的思辨能力；④练习训练，培养解题表达能力；⑤及时反馈，获得信心.

2 制定说的方法

笔者在研究“说数学”的过程中，共经历了以下三个阶段：①自由阶段，教师鼓励学生大胆地说，但迫于教师的压力，效果甚微；②问题阶段，教师根据教学活动需要，设计系列化的问题链，让学生针对问题，一个个地说思路，这种教学效果虽然不错，但存在教师牵着学生鼻子走的嫌疑，制约了学生的自主发挥；③循序渐进阶段，结合教学内容与学生的认知水平，遵循一定的规律、次序，将说数学规划成说、议、辨、练、评，五个层次.

笔者以第三阶段的“说数学”教学为例，针对“分段（复合）函数的零点”的教学，具体谈谈“说数学”的操作过程与方法.

2.1 说开放话题，制造认知冲突

此环节的目的在于引导学生复习零点的概念与性质，强化零点可多元表征的特性.教学中，笔者发现学生在概念的表征上存在模糊性、不灵活性、分散性与不一致性等问题.这些问题会阻碍学生的思维发展.为了帮助学生从高层次理解这些概念，教师可展开以下教学活动.

（1）设计开放话题.封闭式的问题只会禁锢学生的思维，无法达到发散学生思维的目的.本节课，教师可提出：“请大家说说对函数零点的理解.”这是一个典型的开放式问题，学生在回答过程中，思维角度会比较宽泛，在学生畅所欲言时，同伴进行补充，教师在适当的时候进行引导.若学生说对了，紧接着询问理由；若学生说错了，则鼓励同伴进行修正、完善.如此群策群力，即可帮助学生建立完整的知识网络.

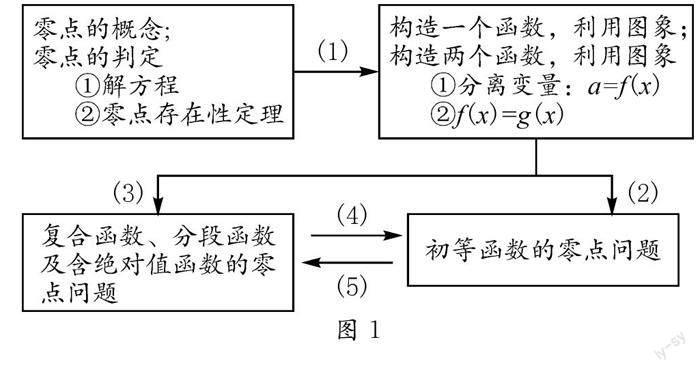
（2）制造认知冲突.每个学生对零点的认识都有所区别，教师可根据学生认知的差异性，通过一定的教学手段激发学生的认知冲突，以激活学生思维的深度与广度.如紧扣“零点不是点”的话题，询问：零点不是点，那是什么？它的本质是什么？有什么作用？等等.学生在对认知冲突的处理中，逐渐实现函数的零点与方程的根的互相转化（见图1）.

2.2 议议新问题，拟定解决方案

这是一个容易被忽视的环节，而此环节却是确定研究对象，激发学生产生学习内驱力的重要机会.首先要建立多元化的对话机制，确定研究对象.如可用：“你们在解决关于零点的问题时，曾经遇到过哪些障碍？”在学生的表达中，师生共同设计解决方案.

如学生在处理f（x）=x2-2x+12的相关问题时，运用了转化为分段函数、整体换元等方法.在学生提出自己的困惑后，师生共同讨论，并获得解决问题的方案为：如图1（4），将分段函数的零点问题转化成初等函数的零点问题.若学生还不能理解这个方法，可例举：已知，f（x）=|x|，g（x）=x2-2x+12，分别求f（g（x））与g（f（x））.

通过上述问题的解决，学生弄清楚了初等函数的零点问题是怎么变成复合分段函数的零点问题.

2.3 辨析新材料，验证解题方案

数学教学并不纯粹是解题教学，而是数学思想方法的教学.“说数学”说的是思维，到底该用怎样的方式来辨析新材料，验证解题方案呢？

首先，在新材料的选择上，可考虑以下几个方面：①可用零点相关知识来解释、分析并解决这个材料；②材料需有新意；③材料要有明确的针对性.其次，在话题的选择上，可从以下流程出发：课前自测、展示错误、错题归因、思考对策、完善解题.再次，在话题的引领上可提出：你用了哪些方法？为什么选择这种方法？还有其他方法吗？这些解题方法错在哪儿？等等.学生亲历思考、辨析过程，可获得思维的升华.

本节课，笔者选择了以下材料：

（1）已知函数f（x）=2|x|，x≤0，|lg x|，x＞0，那么函数g（x）=2f2（x）-3f（x）+1有几个零点？

（2）函数f（x）=|ln x|，如果g（x）=f（x）-ax在区间（0，4）上存在三个零点，那么实数a的取值范围是什么？

（3）若函数f（x）满足以下几个条件：①定义域为R；②x∈R，均有f（2+x）=f（x）；③x∈［-1，1］时，f（x）=1-|x|，则方程f（x）=12log2|x|在区间［-3，5］上有几个解？

以第（2）个材料为例，从多角度进行“说数学”，以培养学生思维的发散性与广阔性.

师：针对第（2）个材料，你们会选择怎样的解题方法？并说说理由.

生1：構造h（x）=ax，分析函数h（x）与f（x）=|ln x|这两个函数的图象（过程略）.

生2：也可以将方程变形为a=|ln x|x，令h（x）=|ln x|x=ln xx，1≤x＜4，-ln xx，0＜x＜1.求导，然后根据h（x）的图象来解决问题（过程略）.

师：还有没有其他方法？

生3：函数g（x）在（0，1）上必然有一个零点.若将问题转化成g（x）在（1，4）上有两个零点，令h（x）=ln x-ax，则h′（x）=1x-a.当a≤0时，h′（x）＞0在（1，4）上恒成立，h（x）最多只有一个零点，因此可排除.当a＞0时，h′（x）的零点为x=1a，此时分0＜1a≤1，1a≥4与1＜1a＜4三种情况进行分析，最终解得ln 22＜a＜1e.

师生都为生3的解题思路喝彩.观察以上解题思路，会发现区间端点特别容易被忽略掉，但学生依然能依靠自主分析完善解题过程.

2.4 练典型例题，培养表述能力

因思维水平的差异，学生的表述能力也有较大差异.为了让学生能想得明白、说得清楚，教师可引导学生通过例题训练、小组交流、同伴互评等方式检验学习成效.如本节课，笔者安排了以下例题进行教学：

（1）已知函数f（x）=x2-2x+1，x＞0，x+1，x≤0，如果关于x的方程f2（x）-af（x）=0有五个不同的实数解，那么a的取值范围是什么？

（2）若f（x）是偶函数，其定义域为R，当x∈［-2，0］时，f（x）=12x-1，如果在区间（-2，6］上关于x的方程f（x）-loga（x+2）=0（a＞1）存在三个不同的实数根，那么a的取值范围是什么？

这是两道关于零点问题的典型例题，学生在这两题的探究过程中，交流合作，最后获得统一结论.笔者要求学生将自己的解题思路、过程与方法分享给大家，如此不仅锻炼了学生的口头表达能力，还让学生在表达的过程中捋清了自己的思路，完善对知识的认知.

2.5 评教学反馈，增强解题信心

及时反馈评价是教学活动不可或缺的一个环节，同一节课，从不同价值观角度出发，会有不一样的评价方式.而不同的评价又会带领学习者朝着不同的方向前进.从教学的时效性出发，回顾与反馈可结合在一起用“说数学”的方式进行.评价方式可多层次、多角度、多元化与多样化.除师生的评价以外，还可吸纳更多外界人士参与到评价中来，以扩大评价元，提高评价效果，增强学生的解题信心.

总之，师生、生生以及生本的“说数学”过程，是多层次的对话过程，也是多维度的思考过程.学生在交流中反馈，又在反馈中交流，最终获得思维的发展与能力的提升，为数学核心素养的形成奠定坚实的基础.