基于值函数迭代的持续监测无人机路径规划

刘晨，陈洋*，符浩

基于值函数迭代的持续监测无人机路径规划

刘晨1，2，陈洋1，2*，符浩3

（1.武汉科技大学 机器人与智能系统研究院，武汉 430081； 2.冶金自动化与检测技术教育部工程研究中心（武汉科技大学），武汉 430081； 3.武汉科技大学 计算机科学与技术学院，武汉 430081）（ ∗ 通信作者电子邮箱chenyag@wust.edu.cn）

使用无人机（UAV）持续监测指定区域可以起到威慑入侵破坏、及时发现异常等作用，然而固定的监测规律容易被入侵者发现，因此需要设计UAV飞行路径的随机算法。针对以上问题，提出一种基于值函数迭代（VFI）的UAV持续监测路径规划算法。首先，合理选择监测目标点的状态，并分析各监测节点的剩余时间；其次，结合奖励/惩罚收益和路径安全性约束构建该监测目标点对应状态的值函数，在VFI算法过程中基于原则和轮盘选择随机选择下一节点；最后，以所有状态的值函数增长趋于饱和为目标，求解UAV持续监测路径。仿真实验结果表明，所提算法获得的信息熵为0.905 0，VFI运行时间为0.363 7 s，相较于传统蚁群算法（ACO），所提算法的信息熵提升了216%，运行时间降低了59%，随机性与快速性均有所提升，验证了具有随机性的UAV飞行路径对提高持续监测效率具有重要意义。

路径规划；持续监测；值迭代；轮盘选择；原则

0 引言

出于公共安全、环境保护、科学研究等目的，人们需要对某些区域进行长期观察、测量和数据采集，从而为系统决策提供支撑，即持续监测问题。人工监测经常受天气、地理环境、熟练程度等影响，导致监测效率低、质量差、成本高，劣势逐步扩大。无人机（Unmanned Aerial Vehicle， UAV）具有飞行稳定、飞行范围广、运行成本较低等优势，同时还能与无人车相结合构成自主监测与数据处理系统，使用无人机或无人车执行监测任务能克服上述人工监测的缺陷。但是使用无人机执行持续监测任务时，为防止入侵者轻易发现监测路径规律，需要提高无人机飞行路线的随机性和监测规律的安全性。本文旨在寻找一个有策略的、安全的持续监测路径计算方法，从而实现持续监测任务的要求。

Cannata等［1］、Portugal等［2］和Machado等［3］在研究持续监测问题时，提出了闲置时间的概念，并将它作为算法性能指标应用于多机器人巡逻问题。闲置时间指巡逻的某个时刻与目标点被访问时刻之间的时间差。Pasqualetti等［4］优化协同巡逻算法最小更新时间，最小更新时间指机器人两次访问同一个位置时的时间间隔。Elmaliach等［5］提出了以一定频率巡逻和访问任务点，根据任务区域中需要访问的任务点构建封闭路径，通过优化路径实现优化目标点被访问的频率的目标。Chen等［6］在研究持续监测问题时，提出一种多蚁群优化（Overdue-aware Multiple Ant Colony Optimization， OMACO）算法，运用目标排他机制求解多无人机合作的最优飞行路径。

近年来，强化学习在自动驾驶［7］、机器视觉［8-9］、自然语言处理［10-11］和推荐搜索系统［12］等领域应用广泛，研究者也开始将强化学习和路径规划结合。Bellman等［13］提出贝尔曼方程和动态规划的概念，根据动态系统的状态和值函数确定函数方程，通过求解该方程得到最优控制解。值迭代是一种动态规划方法，原理是利用奖惩机制学习，每个状态都执行奖赏值最大的动作，使整个过程累积的值最大，从而获得最优策略。马尔可夫决策过程（Markov Decision Process， MDP）是动态规划的离散随机版，通过类似“试错”的机制使方程迭代求解。部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process， POMDP）是处理不确定条件下决策问题的通用框架之一，其中也涉及值迭代算法的应用与改进，代表性的算法包括基于点的值迭代、前向搜索值迭代和启发式搜索值迭代，这些算法通常能够得到最优或近似最优的策略［14］。基于点的值迭代［15］是经典的基于密度标准扩展探索点集的算法。前向搜索值迭代算法［16］采用了基于值函数的近似求解方案，根据最优值函数上界选择最优动作探索最优可达信念点集，保证收敛到全局最优。然而这些算法在大规模问题上存在收敛效率低的缺陷。启发式搜索值迭代［17］采用基于MDP的近似解法，根据MDP的策略在信念点集形成的空间中选择最优的动作，降低了求解复杂度，提高了计算效率。启发式概率值迭代算法相较于主流的基于密度的近似解法能更有效地利用模型信息［18］，相较于基于单一界的近似解法具有更好的收敛效果，相较于基于复合界的解法收敛更快。房俊恒［19］针对大规模POMDP问题，提出了一种改进的启发式搜索值迭代算法。该算法以可达性作为启发式准则搜索具有重大价值的可信状态点，局部更新这些点的值函数，获得了有效的近似优化策略。

Washington等［20］提出了一种简化状态值迭代算法，利用MDP的结构求解最优策略，并将它应用于求解持续监测问题。Bethke等［21］提出一个多智能体持续监视问题的MDP建模方法，讨论了一种由贝叶斯模型估计器与MDP结合的自适应机制，并验证了这种自适应机制在持续监视问题中的性能优势。Jeong等［22］提出一种生成任务流的方法，目标是使持续监视区域的不确定性尽可能保持在较低的水平；实验结果展示了算法具有较小的不确定性，但监视任务的执行过程中仍存在循环轨迹的现象。

上述循环轨迹产生的原因是：在路径规划问题中无人机需在满足约束的前提下从起点运动到达终点，无人机在采用值迭代方法学习路网信息生成最优飞行路径时，通常只能得到唯一最优解，将它融入持续监测任务中，求解得出的无人机路径将是已知起点到某个终点之间路径段的无限循环。为了防止持续监测任务被入侵破坏，不能采用循环路径执行任务，因此本文提出持续监测路径规划算法需要满足随机性要求。陈佳等［23］运用信息熵决定蚁群之间的行动，如合作或是竞争，提高了算法的多样性。

本文围绕持续监测路径规划，在路网和等待时间的约束下，提出一种基于值函数迭代（Value Function Iteration， VFI）的无人机持续监测路径规划算法，寻找一条具有较高安全性的监测路径。值迭代求解方法能快速收敛，求得最优策略近似解；因此，设计并运用值函数进行迭代学习，设计有剩余时间约束的即时收益，结合未来收益，在对每个状态执行奖赏最大的动作时，结合具有随机性的轮盘选择，求出随机性强的持续监测路径最优解，使路径具有一定的安全性。针对给定的初始状态能够输出每次的访问节点，满足收敛阈值的要求。

本文的主要工作包括：

1）考虑持续监测路网和剩余时间约束，结合奖励和惩罚收益，设计值函数建立无人机持续监测路径规划模型。

2）运用具有随机性的轮盘选择的方法，解决无人机监测路径循环问题，在持续监测路径选择下一目标点时，采取原则随机选择其他目标点方法，使用轮盘选择。

3）运用信息熵评价持续监测路径的随机性，其中，每个目标点的熵使用不同访问周期出现的概率进行计算，再通过求取所有目标点的熵的均值评估持续监测路径随机性。

1 问题描述

本文假设持续监测任务由一架旋翼无人机完成。为了方便分析，可以将旋翼无人机视为转弯半径为0、匀速飞行的质点。已知所有待监测目标点构成的拓扑网络和各目标点的最大允许监测周期，其中，目标点的最大允许监测周期指无人机相邻两次监测同一个目标点之间的最大允许时间间隔。如果无人机在该时间间隔之内未能到达相应目标点，表示监测任务失败。

无人机监测过程应当满足以下要求：

1）尽可能提高各个待监测节点的访问频率；

2）相邻两次到达同一个目标点实施监测的间隔时间不允许超过该目标点的最大允许监测周期；

3）监测路径具有较强的随机性。

为了获得无人机最优的监测路径，不允许无人机持续停留在任意一个目标节点的位置。

2 持续监测路径规划模型

城市街道大多是直线形成的矩形区域，因此本文也简化成矩形路网。将待监测区域内的街道设定为无人机持续监测任务的目标点。整个持续监测区域包含多个目标点，每个目标点都拥有各自的最大允许监测周期。因此，每个目标点都有一个表征它的距离发生监测逾期事件的时间间隔的参数，称为监测剩余时间。剩余时间越少，该目标点被监测的需求越迫切。为防止无人机的持续监测规律被入侵者获取，需寻找到安全可靠的持续监测策略，完成对这一区域的持续监测任务。

建立路径规划模型的思路如下：确定无人机的每一个状态，对每个可能的下一目标点计算选择此点后达到下一个状态的期望价值；比较选择哪个目标点达到的状态的期望值函数最大，将这个期望值函数作为当前状态的值函数，并循环执行这个步骤，直到值函数收敛。

2.1　状态向量与动作空间

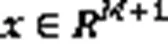
2.2　收益函数

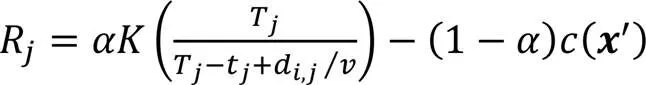
其中sgn为符号函数。

2.3　值函数

无人机决策的目的是期望得到一个行动策略集，但是无人机的决策和行动的奖励不能实时对应。因此，需要定义一个更为有效的函数，即值函数［24］，描述决策和行动的奖励。当前状态的值函数不仅可以横向地与其他状态比较，也可以纵向地与其他策略比较，从而在后续的迭代过程中找到最佳策略，形成行动策略集。

更新后的状态：

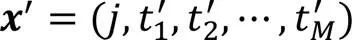
式（7）中，各节点剩余时间的计算如下：

2.4　监测路径的随机性

持续监测任务通常要求监测方案具有一定的随机性，以防止外界获得监测规律伺机破坏，因此有必要在优化监测路径的同时，提升无人机监测路径的随机性。本文通过计算监测路径的信息熵评估监测路径的随机性。信息熵常被用作一个系统的信息含量的量化指标，它表示整个系统的所有信息量的一种期望：系统越复杂，出现不同情况的种类越多，每种情况出现概率越小，随机性越强，信息熵越大；系统越简单，出现情况种类越少，每种情况出现概率越大，随机性越弱，信息熵越小。

无人机在得到行动策略集后，每个目标点被访问的次数不同，同一目标点每次访问的时间间隔不相同，因此持续监测路径中目标点的访问周期是一组离散数。本文运用信息熵评价这一组离散数，信息熵值越高，访问每个目标点的时刻越随机，持续监测路径随机性越强。信息熵函数如下：

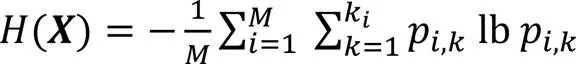
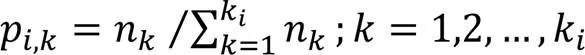
3 模型迭代求解

值迭代算法运行初期，节点被逐渐访问，无法判断有多少种状态向量以及对应的值函数产生。随着迭代次数的增加，状态向量逐渐增多。本文采用值迭代和轮盘选择结合的方法：

3.1　下一节点的选择策略

对于下一目标点的选择，90%概率选择奖励收益最大的目标点，10%概率使用轮盘选择其他目标点。基于轮盘选择的方法的基本思想是：各个目标节点的选择概率与它最大允许监测周期和剩余时间有关。剩余时间越少、与最大允许监测周期的差值越大，被选择的概率越高。具体操作如下：

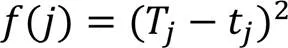
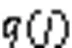
3.2　迭代终止条件

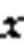
3.3　算法流程

本文针对持续监测问题，建立了基于剩余时间约束的值迭代优化模型。在求解时，首先确定无人机的初始节点，其次根据式（2）初始化各节点监测的剩余时间，最后得到初始状态向量。在执行持续监测任务过程中，通过值函数的迭代优化，当值函数达到收敛条件时，停止迭代，得到无人机最优监测策略。

算法的具体步骤如下：

1）初始化各节点最大允许监测周期和状态向量。无人机从节点1开始执行监测任务，即当=1时，式（1）变为：

4）重复步骤2）～3）搜索无人机路径，直至值函数更新量小于给定的收敛阈值。

算法伪代码见算法1。

算法1 无人机值函数迭代。

循环开始：

综上所述，无人机每从一个监测节点移动到下一监测节点后，将移动后的节点重置为当前节点，继续按照要求寻找移动路径，最终完成持续监测任务，并为无人机规划一条安全的监测路径。

4 实验与结果分析

为了验证本文提出的持续监测无人机路径规划算法的有效性，基于Matlab软件仿真，分别设计了简单路网和复杂路网进行对比分析。本文算法与传统旅行商问题（Traveling Salesman Problem， TSP）中的经典遗传算法（Genetic Algorithm， GA）、模拟退火（Simulated Annealing， SA）算法和蚁群算法（Ant Colony Optimization， ACO）对比。GA通过变异和交叉体现生物遗传的多样性；ACO通过种群间信息素的传递体现集群的智能协作；SA体现经典温度变化规律。简单路网的仿真参数如表1所示。

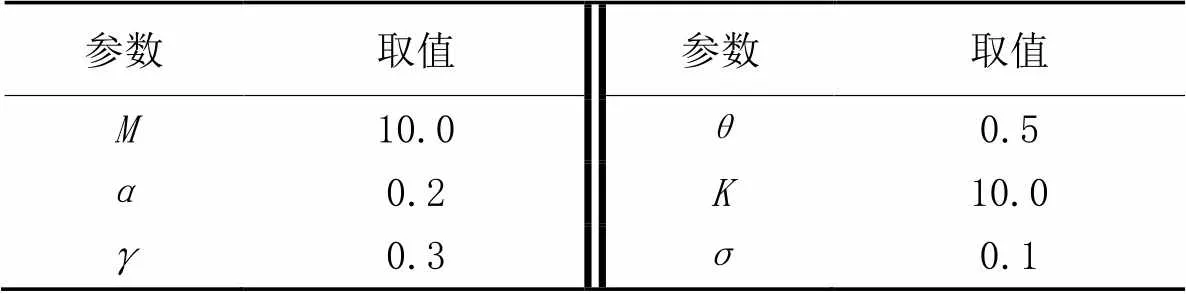
表1　仿真参数

简单路网如图1所示，各节点的最大允许监测周期与坐标如表2所示。无人机初始状态向量的节点位于节点1。

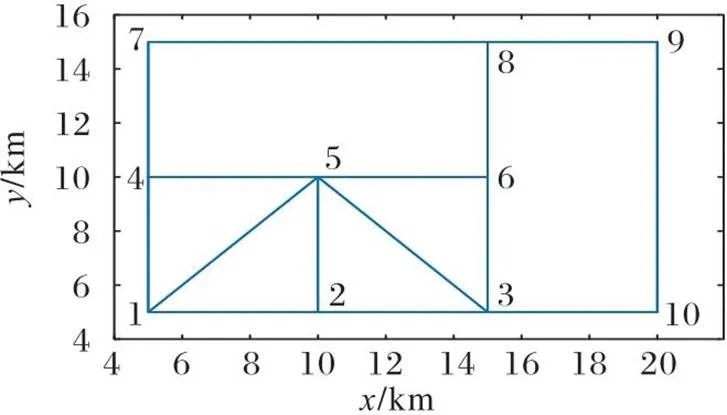
图1　持续监测路网

表2　各节点位置及其最大允许监测周期

4.1　持续监测路径

图2　收敛阈值

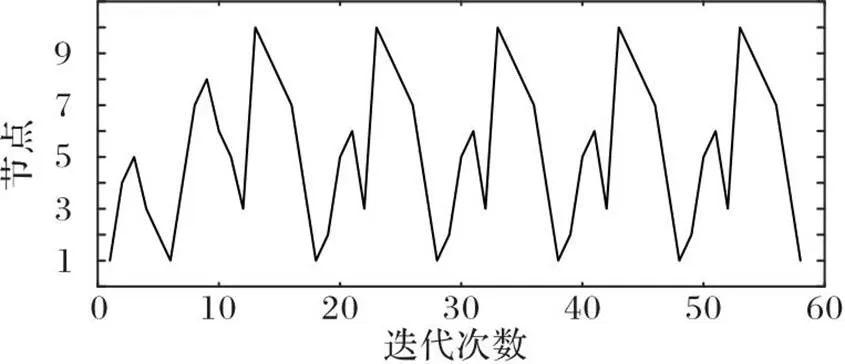
图3　基于VFI的持续监测路径

无人机监测时，若选择不同的初始点，VFI算法得到的概率矩阵有微小差异。以初始点分别为节点1和10为例，得到的概率矩阵灰度图如图4所示。虽然图4（a）和图4（b）的灰度值略有不同，但趋势和主要特征完全一致。因此，无人机每一步决策时基于最大概率得到的路径点相同，这表明即使巡检时初始点不同，仍然会获得稳定的相同的最优路径。

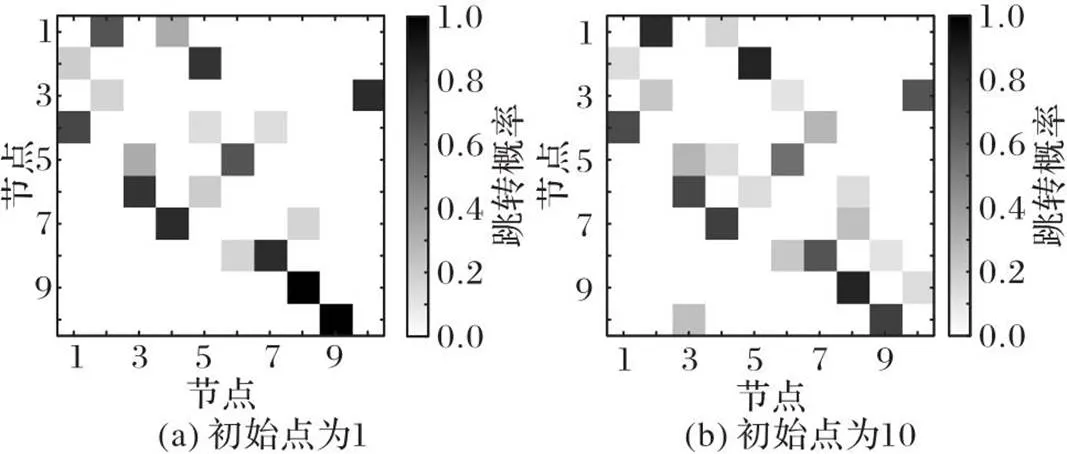
图4　初始点为1和10时概率矩阵灰度图

4.2　持续监测结果随机优化

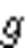
表3　持续监测路径对比

图5中部分状态向量的值函数差值大于0.3，原因为该状态向量的值函数首次更新差值较大且迭代过程中出现次数较少，同时说明了其他状态多次被访问、个别状态很少被访问，排除了持续监测路径循环路径的可能。

图5　三条路径的收敛曲线

图6为3条优化监测路径的部分片段。在整个持续监测路径中，3条路径迭代10步之后，路径节点出现局部循环情况，但它们对应的收敛曲线图中展现出重复的状态少于21个，原因为：状态定义由11个变量构成，状态维度为11，迭代过程运算量较大，在前期少量迭代学习时，仅有的节点数无法满足隐藏的大量状态的匹配。在迭代训练之后，持续监测路径的随机性显著提高，其中路径3的随机性最好，存在循环的路径段仅第6至8步3个目标点，路径1中有第8至17步8个目标点，路径2中有第3至8步6个目标点，存在循环的路径目标点越多，随机性越差。使用信息熵验证基于值函数迭代持续监测路径的随机性，熵值越大，路径中的随机性越强。

图6　三条优化的监测路径

不同算法生成的路径如表4所示，将VFI算法生成的路径1～3用VFI-1、VFI-2、VFI-3表示。

表4　不同持续监测算法的路径结果对比

VFI算法具有以下几个优点：

1）步骤简洁。VFI算法迭代学习一次完整路径，没有ACO中多次迭代完整路径，也没有GA的种群初始化。

2）调参数量少。VFI算法需要提前设定3个参数，GA、ACO和SA分别需要提前设定4、5和4个参数。

3）收敛快。VFI算法遵循奖励收益最大原则迭代学习一次完整路径。GA编码复杂，需要对问题和对应最优解编码，影响收敛速度。ACO使用随机选择，有助于寻找全局最优解，但收敛慢。SA中温度下降速度越慢，搜索时间越长，可以获得更优的解，因此收敛较慢，否则可能跳过最优解。

4.3　实际路网仿真实验

图7　部分城区地图及对应的实际路网

根据图7（b）监测路网展开仿真实验，结果如图8～9所示。整个程序响应时间为0.575 9 s，信息熵为1.576 3，表明在短时间内得到随机性强的持续监测路径。

图8　实际路网下监测路径的收敛曲线

图9　实际路网下的最优持续监测路径

5 结语

随着网络中目标点增多，状态向量维数也会增加，采用单架无人机监测可能无法满足每个目标点的最大允许监测周期，因此，未来工作将研究多无人机的协作持续监测问题。

[1] CANNATA G， SGORBISSA A. A minimalist algorithm for multirobot continuous coverage［J］. IEEE Transactions on Robotics， 2011， 27（2）： 297-312.

[2] PORTUGAL D， ROCHA R P. Multi-robot patrolling algorithms： examining performance and scalability［J］. Advanced Robotics， 2013， 27（5）： 325-336.

[3] MACHADO A， RAMALHO G， ZUCKER J D， et al. Multi-agent patrolling： an empirical analysis of alternative architectures［C］// Proceedings of the 2002 International Workshop on Multi-Agent Systems and Agent-Based Simulation， LNCS 2581. Berlin： Springer， 2003： 155-170.

[4] PASQUALETTI F， FRANCHI A， BULLO F. On cooperative patrolling： optimal trajectories， complexity analysis， and approximation algorithms［J］. IEEE Transactions on Robotics， 2012， 28（3）： 592-606.

[5] ELMALIACH Y， AGMON N， KAMINKA G A. Multi-robot area patrol under frequency constraints［J］. Annals of Mathematics and Artificial Intelligence， 2009， 57（3/4）： 293-320.

[6] CHEN Y， SHU Y， HU M， et al. Multi-UAV cooperative path planning with monitoring privacy preservation［J］. Applied Sciences， 2022， 12（23）： No.12111.

[7] ZHANG H， ZHAO J， WANG R， et al. Multi-objective reinforcement learning algorithm and its application in drive system［C］// Proceedings of the 34th Annual Conference of IEEE Industrial Electronics. Piscataway： IEEE， 2008： 274-279.

[8] OH J， GUO X， LEE H， et al. Action-conditional video prediction using deep networks in Atari games［C］// Proceedings of the 28th International Conference on Neural Information Processing Systems — Volume 2. Cambridge： MIT Press， 2015： 2863-2871.

[9] CAICEDO J C， LAZEBNIK S. Active object localization with deep reinforcement learning［C］// Proceedings of the 2015 IEEE International Conference on Computer Vision. Piscataway： IEEE， 2015： 2488-2496.

[10] LEWIS M， YARATS D， DAUPHIN Y， et al. Deal or no deal？ end-to-end learning of negotiation dialogues［C］// Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Stroudsburg， PA： ACL， 2017： 2443-2453.

[11] WEISZ G， BUDZIANOWSKI P， SU P H， et al. Sample efficient deep reinforcement learning for dialogue systems with large action spaces［J］. IEEE/ACM Transactions on Audio， Speech， and Language Processing， 2018， 26（11）： 2083-2097.

[12] DERHAMI V， PAKSIMA J， KHAJAH H. Web pages ranking algorithm based on reinforcement learning and user feedback［J］. Journal of AI and Data Mining， 2015， 3（2）： 157-168.

[13] BELLMAN R. On the theory of dynamic programming［J］. Proceedings of the National Academy of Sciences of the United States of America， 1952， 38（8）： 716-719.

[14] BRAVO R Z B， LEIRAS A， CYRINO OLIVEIRA F L. The use of UAV s in humanitarian relief： an application of POMDP-based methodology for finding victims［J］. Production and Operations Management， 2019， 28（2）： 421-440.

[15] BURKS L， AHMED N， LOEFGREN I， et al. Collaborative human-autonomy semantic sensing through structured POMDP planning［J］. Robotics and Autonomous Systems， 2021， 140： No.103753.

[16] AKBARINASAJI S， KAVAKLIOGLU C， BAŞAR A， et al. Partially observable Markov decision process to generate policies in software defect management［J］. Journal of Systems and Software， 2020， 163： No.110518.

[17] HORÁK K， BOŠANSKÝ B， PÉCHOUČEK M. Heuristic search value iteration for one-sided partially observable stochastic games［C］// Proceedings of the 31st AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2017：558-564.

[18] LIU F， HUA X， JIN X. A hybrid heuristic value iteration algorithm for POMDP［C］// Proceedings of the IEEE 28th International Conference on Tools with Artificial Intelligence. Piscataway： IEEE， 2016： 304-310.

[19] 房俊恒. 基于点的值迭代算法在POMDP问题中的研究［D］. 苏州：苏州大学， 2015： 25-35.（FANG J H. Research on point-based value iteration algorithms in POMDP domains［D］. Suzhou： Soochow University， 2015： 25-35.）

[20] WASHINGTON P H， SCHWAGER M. Reduced state value iteration for multi-drone persistent surveillance with charging constraints［C］// Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway： IEEE， 2021： 6390-6397.

[21] BETHKE B， BERTUCCELLI L， HOW J P. Experimental demonstration of adaptive MDP-based planning with model uncertainty［C］// Proceedings of the 2008 AIAA Guidance， Navigation and Control Conference and Exhibit. Reston， VA： AIAA， 2008： No.6322.

[22] JEONG B M， HA J S， CHOI H L. MDP-based mission planning for multi-UAV persistent surveillance［C］// Proceedings of the 14th International Conference on Control， Automation and Systems. Piscataway： IEEE， 2014： 831-834.

[23] 陈佳，游晓明，刘升，等. 结合信息熵的多种群博弈蚁群算法［J］. 计算机工程与应用， 2019， 55（16）：170-178.（CHEN J， YOU X M， LIU S， et al. Entropy-game based multi-population ant colony optimization［J］. Computer Engineering and Applications， 2019， 55（16）：170-178.）

[24] HA M， WANG D， LIU D. Generalized value iteration for discounted optimal control with stability analysis［J］. Systems and Control Letters， 2021， 147： No.104847.

UAV path planning for persistent monitoring based on value function iteration

LIU Chen1，2， CHEN Yang1，2*， FU Hao3

（1，，430081，；2（），430081，；3，，430081，）

The use of Unmanned Aerial Vehicle （UAV） to continuously monitor designated areas can play a role in deterring invasion and damage as well as discovering abnormalities in time， but the fixed monitoring rules are easy to be discovered by the invaders. Therefore， it is necessary to design a random algorithm for UAV flight path. In view of the above problem， a UAV persistent monitoring path planning algorithm based on Value Function Iteration （VFI） was proposed. Firstly， the state of the monitoring target point was selected reasonably， and the remaining time of each monitoring node was analyzed. Secondly， the value function of the corresponding state of this monitoring target point was constructed by combining the reward/penalty benefit and the path security constraint. In the process of the VFI algorithm， the next node was selected randomly based onprinciple and roulette selection. Finally， with the goal that the growth of the value function of all states tends to be saturated， the UAV persistent monitoring path was solved. Simulation results show that the proposed algorithm has the obtained information entropy of 0.905 0， and the VFI running time of 0.363 7 s. Compared with the traditional Ant Colony Optimization （ACO）， the proposed algorithm has the information entropy increased by 216%， and the running time decreased by 59%，both randomness and rapidity have been improved. It is verified that random UAV flight path is of great significance to improve the efficiency of persistent monitoring.

path planning; persistent monitoring; value iteration; roulette selection;principle

This work is partially supported by National Natural Science Foundation of China （62173262， 62073250）.

LIU Chen， born in 1998， M. S. candidate. His research interests include robot navigation and path planning.

CHEN Yang， born in 1980， Ph. D.， professor. His research interests include modeling， planning and control of mobile robots.

FU Hao， born in 1988， Ph. D.， lecturer. His research interests include multi-robot reinforcement learning.

1001-9081（2023）10-3290-07

10.11772/j.issn.1001-9081.2022091464

2022⁃09⁃30；

2023⁃01⁃13；

国家自然科学基金资助项目（62173262，62073250）。

刘晨（1998—），男，湖北洪湖人，硕士研究生，主要研究方向：机器人导航与路径规划； 陈洋（1980—），男，湖北荆门人，教授，博士，主要研究方向：移动机器人建模、规划与控制； 符浩（1988—），男，湖南桃江人，讲师，博士，主要研究方向：多机器人强化学习。

TP242；TP18

A

2023⁃01⁃15。