基于谱聚类的社交网络动态社区发现算法

杨煜，段威威

基于谱聚类的社交网络动态社区发现算法

杨煜*，段威威

（电子科技大学 计算机科学与工程学院，成都 611731）（ ∗ 通信作者电子邮箱yangyu2022@std.uestc.edu.cn）

动态社区发现研究是社交网络分析（SNA）的重要研究领域。随着节点加入或离开社交网络，节点间的关系也随之建立或消失，进而影响着社区结构的变化。针对社交网络静态社区发现算法缺少必要的社区节点历史信息而导致的网络结构分析、聚类信息不足和计算开销过大的问题，基于社区网络演化事件的划分并根据主要社区事件的分析，提出一种基于谱聚类的动态社区发现算法（SC-DCDA）。首先，根据实验观察使用谱映射的方法将高维数据降维，并采用改进的模糊C-均值聚类（FCM）算法确定动态社交网络中的节点与待发现社区的关联度；其次，根据演化相似度矩阵分析社区结构。通过使用真实网络数据集以及模块度得分、轮廓系数等社区发现算法衡量指标，评估所提算法的效果。实验结果表明，SC-DCDA的计算开销相较于传统谱聚类降低了8.37%，在所有数据集上的平均模块度得分是0.49，其他衡量指标的定性分析结果也较好，验证了所提算法在信息交互、聚类效果和精确度上表现较好。

社交网络分析；动态社区发现算法；模糊C-均值聚类；演化相似度矩阵

0 引言

社区是社交网络中拓扑结构的重要研究对象，社区发现算法是社交网络分析（Social Network Analysis， SNA）的主要研究领域，研究社区发现算法有助于研究者深入学习社交网络的复杂拓扑结构及其社区行为特征。传统社交网络社区发现算法的研究对象多为静态社区，然而实际的社交网络都是随时间的变化而不断演化，导致多数静态社区发现建模研究难以识别同一社区中节点随时间变化所具有的相同或相似的属性及其行为，更难以识别不同社区中的节点随时间变化所具有的潜在信息，无法有效提取动态社区的特征，分析动态网络结构、网络特性、网络信息传播规律和优化网络应用不准确。

动态社区由一组连接紧密、随时间变化的节点组成，并且社区内部节点在此刻比社区外部节点连接更紧密。社交网络动态社区发现是在随时间变化的复杂网络系统中，发现连接紧密的社区结构。研究动态社区的网络建模、行为分析和社区发现算法能有效揭示社交网络中节点和连接特征、节点和连接社区的共性规律，有助于推动社区发现算法相关应用。它的研究意义是探究复杂网络结构及社区事件演化的过程，为社交网络的应用提供支撑。

目前，动态社交网络社区发现算法面临的问题是动态网络模型的构建。现有的动态模型构建方法通常采用融合非隐匿平滑框架的策略［1-2］，该策略可以量化社区时间片间的相似性，通过拓展静态社区发现的方法，借助网络拓扑结构的连通性和模块度函数发现动态社区的结构；在概率模型中，使用贝叶斯模型根据扩展随机块模型计算演化的动态社区结构。在模型构建中，不同社区之间动态交互结构通常是稀疏关系，导致它们的相似度矩阵也是稀疏相似度矩阵，影响谱聚类算法的收敛。同时，动态模型中社区数随着相邻时间片的节点交互而动态演化，演化决定着社区的合并和分裂、生长和收缩、产生和消失及持续保持，致使在设计算法中社区数难以确定。综上，现阶段稀疏相似度矩阵对谱聚类算法和确定相邻时间片动态社区数的相关研究较少。

针对社交网络动态社区建模中存在的上述问题，提出基于谱聚类的动态社区发现算法（Spectral Clustering based Dynamic Community Discovery Algorithm， SC-DCDA）。

本文的主要工作如下：

1）针对稀疏矩阵的影响，改进谱聚类算法。基于谱映射优化方法提取的社交网络拓扑结构的特征值，使用模糊C-均值聚类（Fuzzy C-Means clustering， FCM）算法确定动态社交网络的节点与待发现社区的关联程度，即计算数据集数据点间的相似度，通过谱映射优化将网络中节点转化成谱聚类算法的近似相似度度量矩阵，降低稀疏矩阵对谱聚类算法的影响，减少动态谱聚类计算的开销。

2）针对确定动态社区数，考虑网络社区的历史时间片拓扑结构特征，将当前时间片的社区拓扑结构状态信息和它的历史时间片的拓扑结构状态信息进行谱聚类。根据事件演化相似度矩阵确定动态社区数，分析和预测时间片上社区事件的演化结果。

3）在真实的CollegeMsg［1］、email-Eu-core-temporal［2］、sx-askubuntu［2］和wiki-talk-temporal［2］动态网络数据集的时间片上，对比SC-DCDA和典型算法的计算开销和性能，实验结果验证了所提算法在信息交互、聚类效果和精确度上均表现较好。

1 相关工作

本文重点关注社交网络动态社区结构演化规律和社区发现算法。关于动态社交网络社区结构发现算法的研究，Li等［3］归纳出时间权衡社区发现方法和跨时间片社区发现方法，其中：时间权衡社区发现方法的思想是社区结构发现的更新依赖于当前社交网络状态和前一时间片网络结构信息，该方法较接近现实社交网络场景；跨时间片社区发现方法的思想是在不同时间片上社区结构发现更新依赖于过去、当前社交网络状态中所有可获得到的有效信息，该方法认为对社交网络的生命周期进行时间片划分，使得相邻时间片社区结构关系具有随机性和不确定性。动态社区结构演化和社区发现研究的目标是识别具有较高相似度节点及较高关联度的社区。

由于社交网络动态社区的开放性、动态性和复杂性，发现算法主要关注社区划分结果的精确度、事件动态演化、动态社区发现算法和社区发现算法质量评价标准等方面：Yin等［4］提出改进的粒子算法，对初始聚类结果调优，防止聚类局部最优化，提高聚类的精确度；Wang等［5］提出基于马尔可夫链的动态过程增加社区检测算法动态过程的转移概率，提高社区检测的能力；Besharatnia等［6］提出标签传播的优化方法，提高动态社区检测的质量和效率；Li等［7］提出局部谱子图（LOcal SPectral clustering， LOSP）的局部重叠社区发现方法；Wharrie等［8］、Mucha等［9］和Palla等［10］提出社区发现算法社区质量评价标准，社区质量评价标准主要包括核函数、模块度和进化聚类社区质量评价方法，分别用于评价动态社交网络社区检测近似度变化、相邻时间片社区结构变化和检测社区质量差异度。

1.1　相似度的计算方法

相似度是社交网络社区发现中建模节点属性和行为的相似程度的衡量指标，如边介数（Betweeness）衡量指标［11］。边介数指网络中任意节点之间通过此边的最多路径数，并且介数高的边比介数低的边更可能是社区间的边。不同社区中节点之间的最短路径都经过社区间的这条边，这为社区发现提供相似度计算的依据。

通过相似度分析可以研究社交网络社区节点特征值，除常用的密度、距离、聚集系数等方法之外，现有研究使用的相似度计算方法逐渐向综合性的相似度计算方法发展。Li等［12］提出基于节点特征值、关系密度和拓扑结构的多相似度计算方法；Qin等［13］提出多相似度谱方法改进已有进化聚类相似度计算准确度，该方法更好地用于检测动态网络的社区结构；Chen等［14］使用微分方程模拟有向网络中节点的连续变化状态，提出基于重构邻居集（节点基于自身状态和正向连接邻居集的平均状态，以及社区间正向连接相似度关系更新状态）的进化谱算法，较好地检测动态网络的社区结构；Olszewski等［15］提出在输入输出数据空间中改进数据样本邻居计算方法，该方法基于数据的离散性，自适应计算数据宽度，先输入数据聚类，再计算聚类内差异值，最后依据此值决定数据样本邻居宽度值进行社区分割；Guidi等［16］定义邻接区域结构，节点间拓扑结构相似度分析基于相对熵（节点间关于邻接区域信息分布的相似度度量）计算节点间的相似度。综上，基于距离的相似度计算将忽略节点携带信息的相似度，相较于距离计算的社区发现更重要。

1.2　谱映射和模糊C-均值

谱映射建立矩阵特征向量特征值与多项式的函数关系，即在社交网络不同时间片上使用谱映射方法提取网络的拓扑结构的特征值，使用FCM根据提取的特征值发现社区。与C-means相比，FCM的划分引入了弹性空间。与-means相比，FCM的目标函数中引入了隶属度矩阵，指明节点属于待划分社区的隶属程度，并且-means理论上只是确保快速收敛到局部最优解（因为聚类内节点对初始聚类中心点的选择具有依赖性），即-means最优解的求解要求对网络划分所有可能的社区。本文使用FCM，通过算法迭代后，根据终止迭代条件将节点划分到隶属度较高的社区。

1.3　静态到动态社区发现算法

如图1所示，CollegeMsg原始数据集（包含1 899个节点和5 983条边）来自https：//snap.stanford.edu/data/CollegeMsg.html，实验中根据事件演化人为划分8 000、16 000和24 000条数据记录。图1（c）是整个CollegeMsg数据集193 d的动态可视化结构，社交网络静态社区结构发现到动态社区结构发现随时间推移的过程。

图1　CollegeMsg原始数据集的可视化结构

图2为不同时间片上动态社区结构发现的结构演变，SC-DCDA的社区结构演变基于当前社交网络拓扑结构状态信息和前一相邻时间片拓扑结构状态信息。

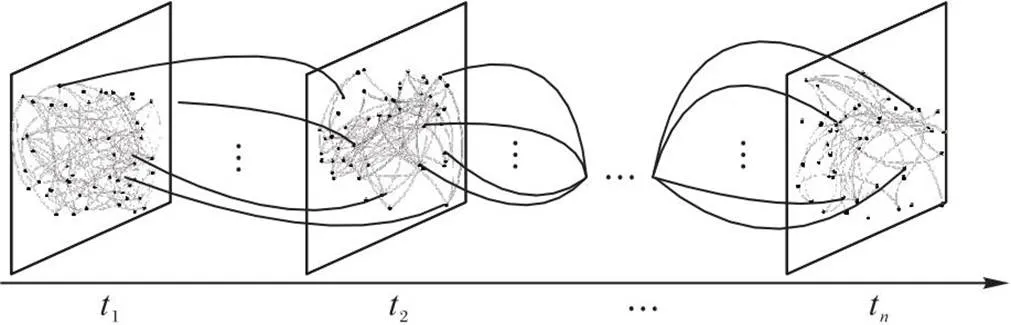
图2　动态社区结构的时间依赖图

静态社区发现算法较难识别同一社区中的节点随时间片迁移所具有的相同或相似属性、行为，更难识别不同社区节点随时间片迁移所具有的潜在信息。在社区发现算法中引入时间片概念划分结构演化过程事件，建立演化模型过渡到动态社区发现算法，更精确地分析网络结构、特性和信息传播规律，进而将时间片上的局部最优社区结构向整个网络演化的全局最优社区结构求解。

2 动态社交网络结构和演化

2.1　社区结构相关定义

社区结构是自底向上分析复杂社交网络拓扑结构的重要分析方法，本文为便于阐述基于谱聚类的社交网络社区发现算法，将社区结构定义如下。

2.2　动态社区结构演化

鉴于社交网络的复杂性及其网络规模难以量化，为便于研究基于谱聚类的社交网络社区发现算法和人为划分时间片，本文引入动态社区结构演化。

社区结构发现以节点具有相同或相似的属性、行为及其连接关系建模。随着时间的不断变化，根据新的节点及其连接关系在网络中的出现，以及原有节点及其连接关系的不断变化，将社交网络社区结构的演化划分为出生事件、死亡事件、生长事件、分裂事件、合并事件、持续事件和收缩事件等节点重组的演化过程事件。结合Guidi等［16］定义的相似度矩阵（式（1））和Mohammadmosaferi等［17］引入事件的部分进化。

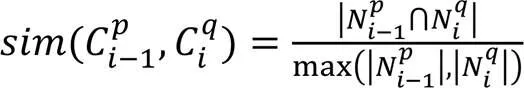
针对动态社区发现的理论基础工作，演化相似度矩阵定义如下。

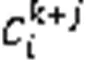
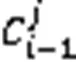
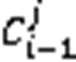
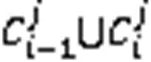
此外，过往研究还将事件细化为：持续事件（Continue Event）、收缩事件（Contraction Event）和生长事件（Growth Event）。在演化过程事件中，出生事件和死亡事件对社区结构新增和删除的影响最大，因此基于谱聚类的社交网络社区发现算法重点关注这两类事件，难点是关注分裂事件和合并事件。

基于谱聚类的社交网络社区发现算法整体思想为：将时间上有限的动态社区网络结构人为地划分成具体的时间片，再使用静态谱聚类或其他对比算法处理网络相邻连续时间片上的社区结构，分析和预测时间片上社区事件演化结果，得到相邻连续时间片上（当前时间片和前一时间片）谱聚类动态社区。

3 基于谱聚类的动态社区发现算法

基于谱图理论的聚类算法是社交网络动态社区发现的研究方法之一，社交网络社区发现聚类算法是将聚类问题转化为图最优划分问题，原因是谱聚类算法计算社交网络的最小割，与相似度矩阵和拉普拉斯矩阵（Laplacian matrix）特征值一致。本文算法基于时间权衡社区发现方法的启发，提出基于FCM的谱聚类算法计算动态社区。

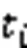
为了确定动态建模中社区数，考虑在每一个时间片上发现当前网络和历史网络特征的社区数和结构，克服静态社区发现算法仅考虑历史网络特征的社区数和结构的缺点。SC-DCDA的流程分3个步骤。

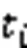
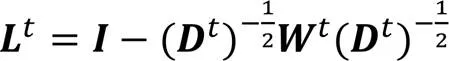
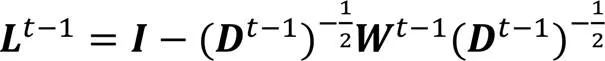
第三步 根据第2章动态社区结构事件演化，基于谱聚类算法求解当前网络和历史网络特征的社区数和结构。

SC-DCDA具体的伪代码如算法1所示。

算法1 基于谱聚类的动态社区发现算法。

end for

end if

动态社区结构发现按照时间片序列，对每个时间片上的网络运用谱映射优化，将网络中节点转化成谱聚类算法的近似相似度度量矩阵，使用Minkowski distance公式作为相似度的简化度量；应用拉普拉斯特征处理，将特征数据转换成适合SC-DCDA的特征矩阵；基于事件演化模型，模拟动态社交网络社区结构算法计算聚类结果，SC-DCDA记录社区结构演化事件。

4 实验与结果分析

主要从获取真实动态社交网络数据集、数据处理、特征处理、FCM谱聚类、动态社区演化模型训练、算法调优、算法预测值输出和算法性能评估方面验证本文算法的准确度和有效性。

4.1　数据集

实验在数据集CollegeMsg［1］、email-Eu-core-temporal［2］、sx-askubuntu［2］和wiki-talk-temporal［2］的不同时间片上进行，消融实验、性能分析实验和对比实验中所使用的动态网络真实数据集均来自网络，数据集的统计信息如表1所示。特别的，数据集节点和链接之间关系的结构和属性需要转换成Python语言支持的.gml数据类型和存储。

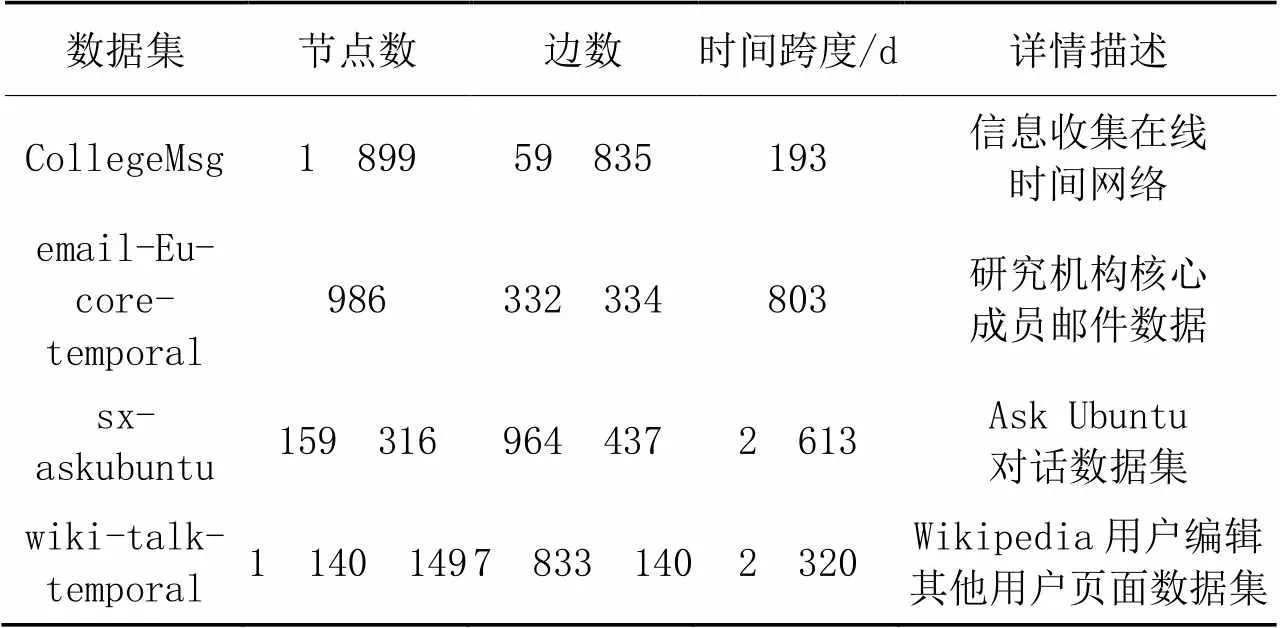
表1　数据集统计信息

4.2　性能评价指标

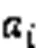
3）CH（Calinski-Harabasz）指标［21］。聚类模型质量的评价指标，即相同类别相似性较高，不同类别相似性较低。值越高，聚类模型的质量越好。

4）Davies-Bouldin指数（Davies-Bouldin Index， DBI）［21］。聚类算法聚类质量的评估指标，聚类内距离之和与聚类间距离之比，比值越小，聚类效果越好。

4.3　实验环境设置

算法实现使用Python语言，运行时间单位为s。处理器信息为配备Radeon显卡的AMD 锐龙 7 5800H，主频为3.20 GHz，内存容量是16.0 GB。

4.4　实验结果与分析

不同的社区发现算法会产生不同的社区分布和运行时间，实验中使用的数据集时间片来自表1数据集的手动分片，保证相邻时间片社区结构演化的相似度，当前时间片的分片时间跨度包含上一相邻时间片的时间跨度。

将数据集划分为3个时间跨度的时间片，即CollegeMsg 0.8、CollegeMsg 1.6、CollegeMsg 2.4，email-Eu-core-temporal 1、email-Eu-core-temporal 6、email-Eu-core-temporal 12，sx-askubuntu 2.5、sx-askubuntu 5、sx-askubuntu 7.5，wiki-talk-temporal 2.5、wiki-talk-temporal 5和wiki-talk-temporal 7.5。其中0.8指8 000条数据集记录，依此类推，时间片跨度为当地时间2004年4月15日22：56至2004年5月4日14：24。

如表2所示，SC-DCDA基于社区事件演化相似度矩阵的改进的FCM谱聚类，在消融实验中，SC-DCDA的计算稀疏矩阵的时间开销相较于传统谱聚类降低了8.37%，主要原因是SC-DCDA采用时间权衡社区发现方法，社区结构发现的更新不仅考虑当前社交网络状态，也考虑前一时间片网络结构信息，该时间片上没有演化的节点聚类的时间开销则降低。

在与典型算法对比实验中，对比算法分别选择基于遍历策略求最大模块度的Louvain算法［22-23］、基于最小熵原理求最优解的InfoMap算法［24］、基于贪心策略的最大团合并的Fast Newman（FN）算法［24］和基于边介数（任意两节点间通过此边的最短路径数）的Girvan-Newman（GN）算法［22-23］。从图3可知，SC-DCDA在各个数据集上随着时间片的时间跨度不断增加，但相较于其他对比算法，增长较缓慢，表明SC-DCDA的运行时间的增长率没有显著增长，进而说明它在不同时间片上具有较好的可扩展性。

使用无标签的CollegeMsg、email-Eu-core-temporal、sx-askubuntu和wiki-talk-temporal数据集，分别在3个时间片上与Louvain算法、InfoMap算法、FN算法和GN算法对比模块度得分，结果如图4所示。在真实数据集上，模块度得分在0.5～0.7的聚类算法效果较好。SC-DCDA在email-Eu-core-temporal数据集时间片的平均模块度得分是0.60，在上述数据集平均模块度得分是0.49，具有较好的聚类效果。

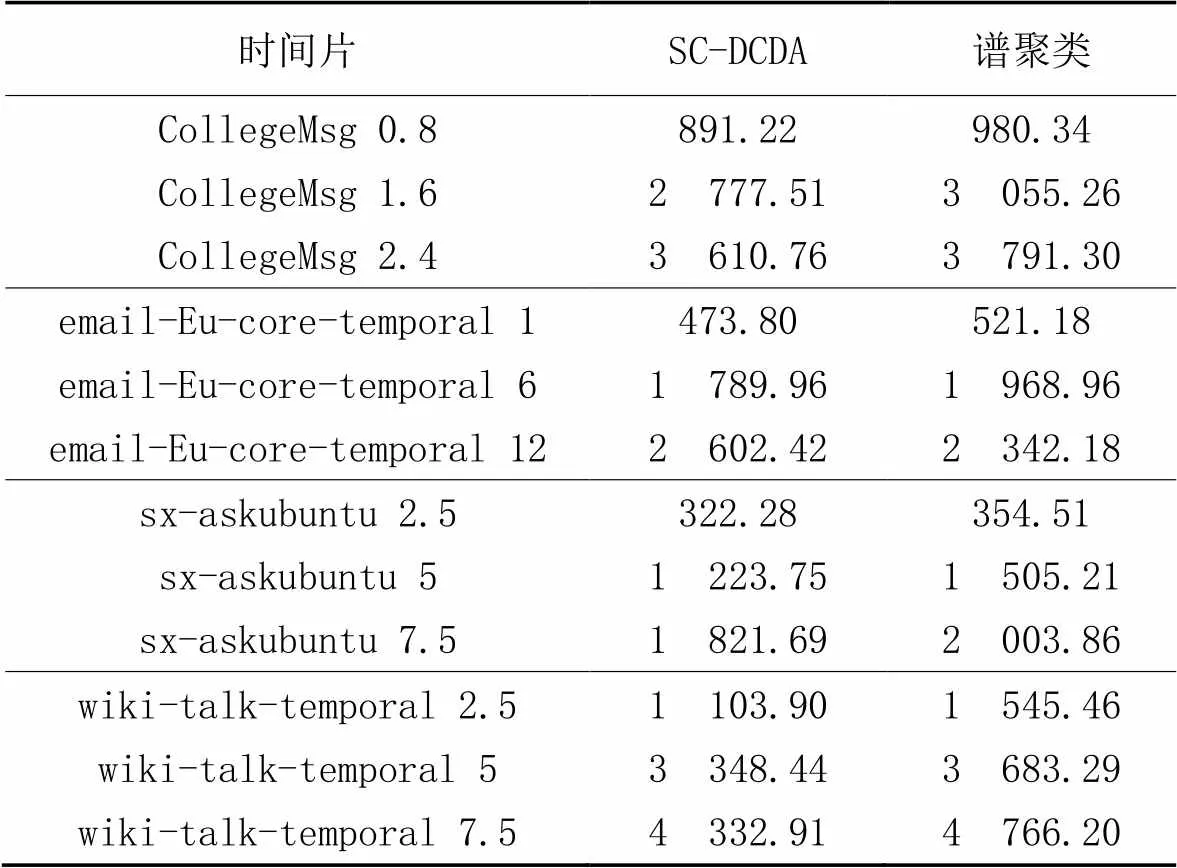
表2　SC-DCDA与谱聚类在动态数据集上的计算开销对比

图3　SC-DCDA与典型算法在动态数据集上的运行时间对比

使用轮廓系数评价社区发现结果的准确性。实验使用上述无标签数据集分别在3个时间片上与典型算法的轮廓系数对比：该评价指标越接近1，说明样本聚类正确性越高；越接近-1，说明聚类的错误概率越高。从图5可以看出，相较于其他算法，SC-DCDA聚类的轮廓系数均为正数，社区发现的正确性较好，并且无错误聚类的指标概率。

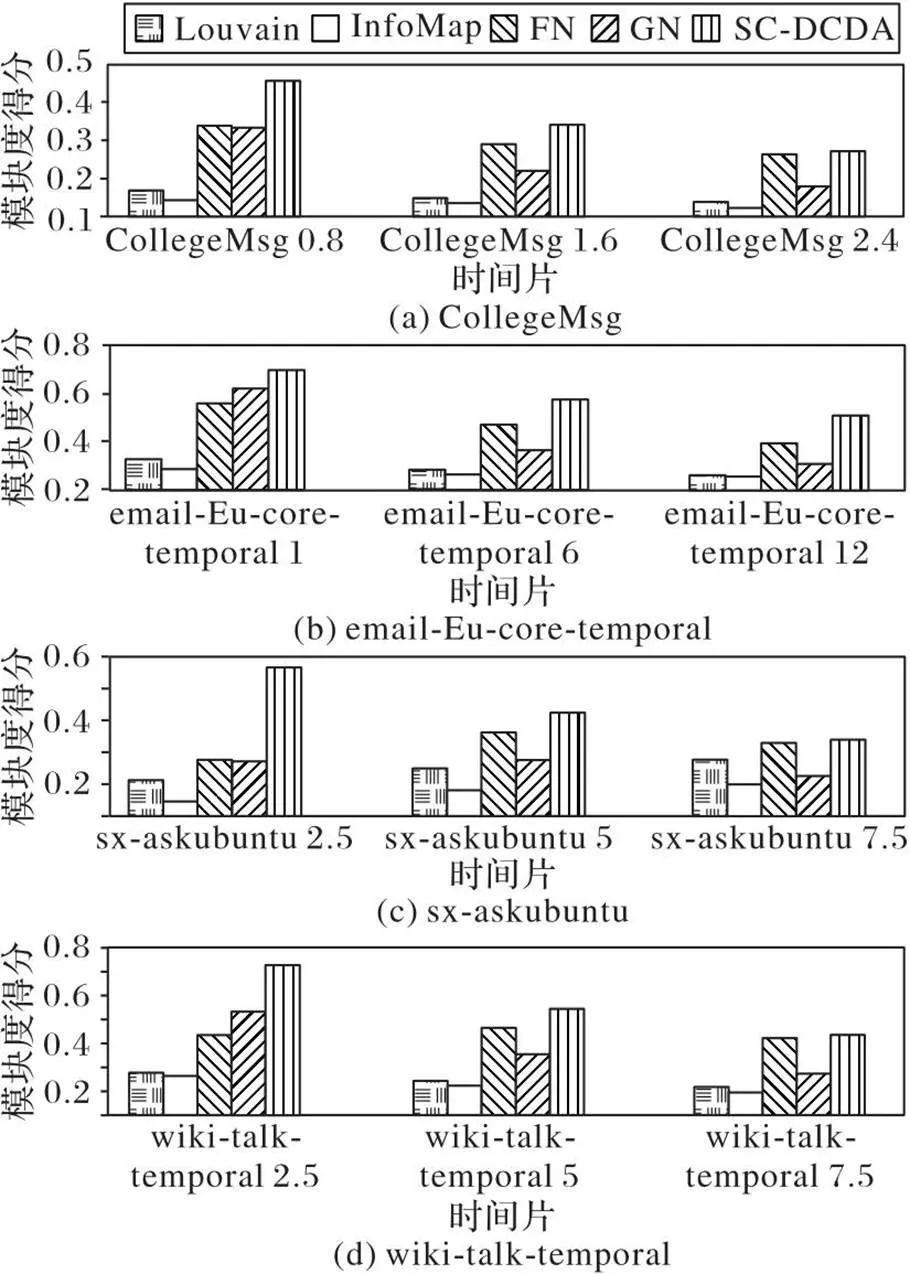
图4　SC-DCDA与典型算法的模块度得分对比

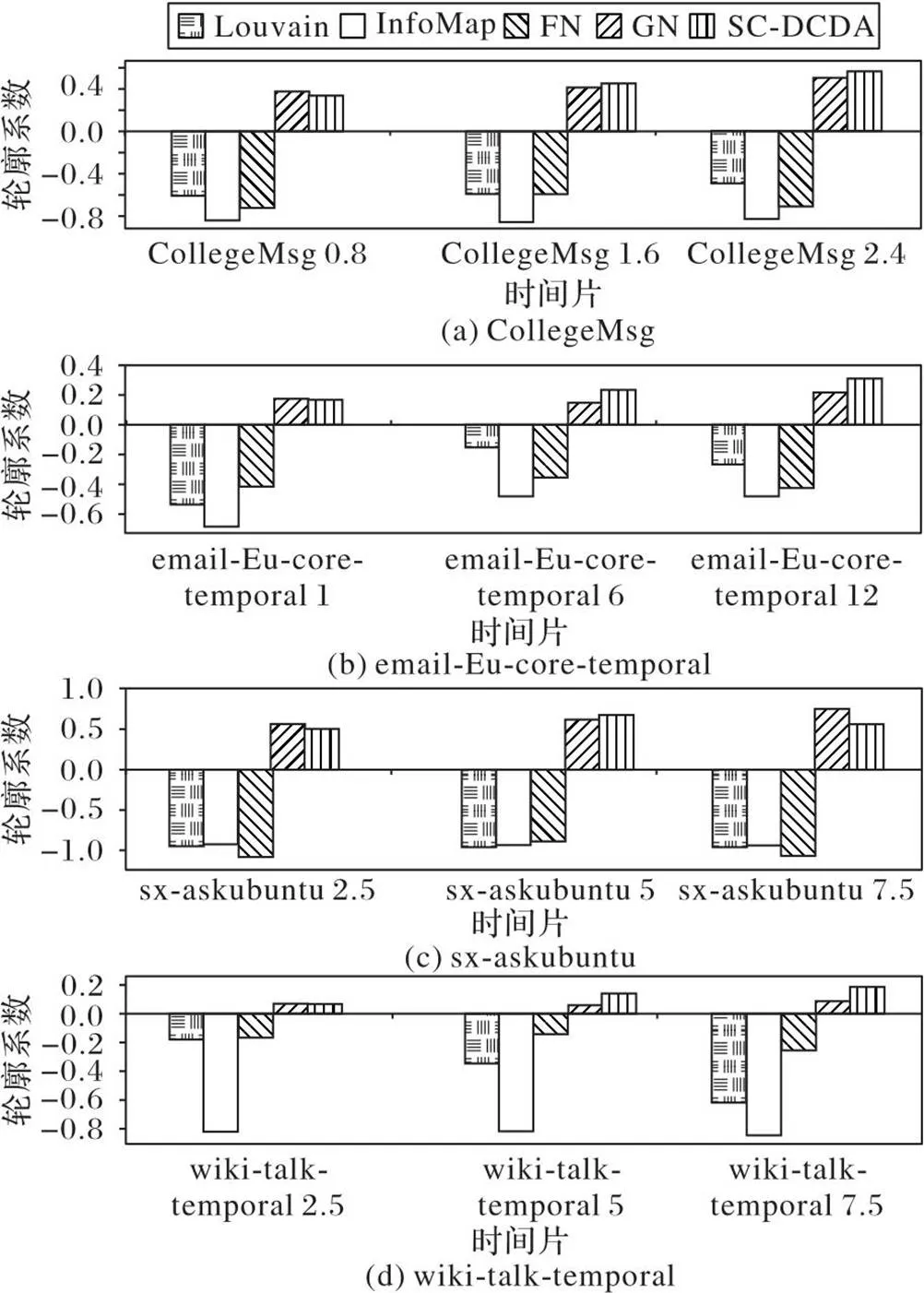
图5　SC-DCDA与典型算法的轮廓系数指标对比

此外，使用CH和DBI指标评价社区发现结果的质量。从图6可以看出，GN算法和SC-DCDA的CH平均值均高于其他对比算法，模型的聚类效果较好。从图7可以看出，SC-DCDA的DBI平均值较小，说明它取得了较好的社区发现结果。实验中根据DBI值不断优化FCM聚类，防止产生局部最优解。

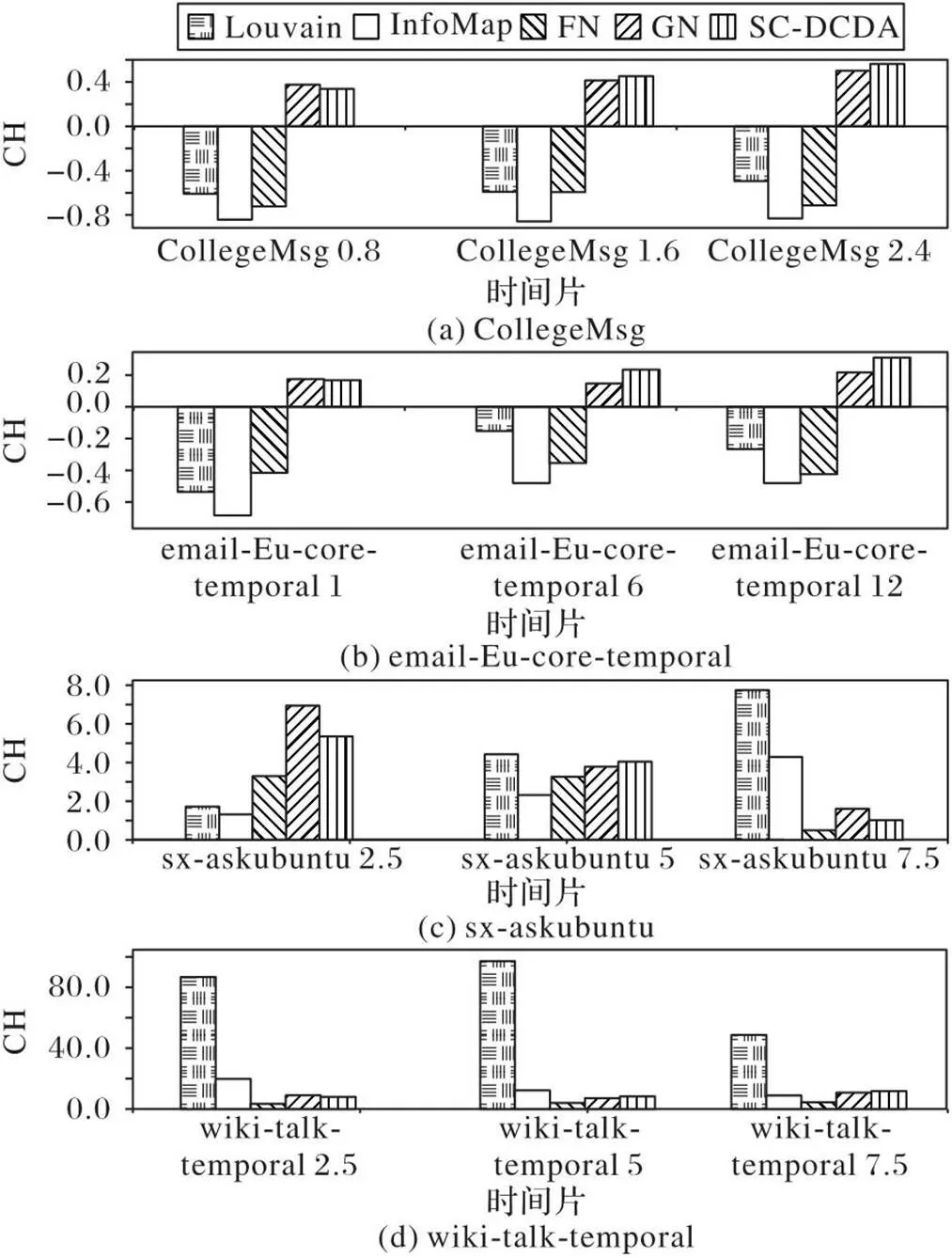
图6　SC-DCDA与典型算法的CH指标对比

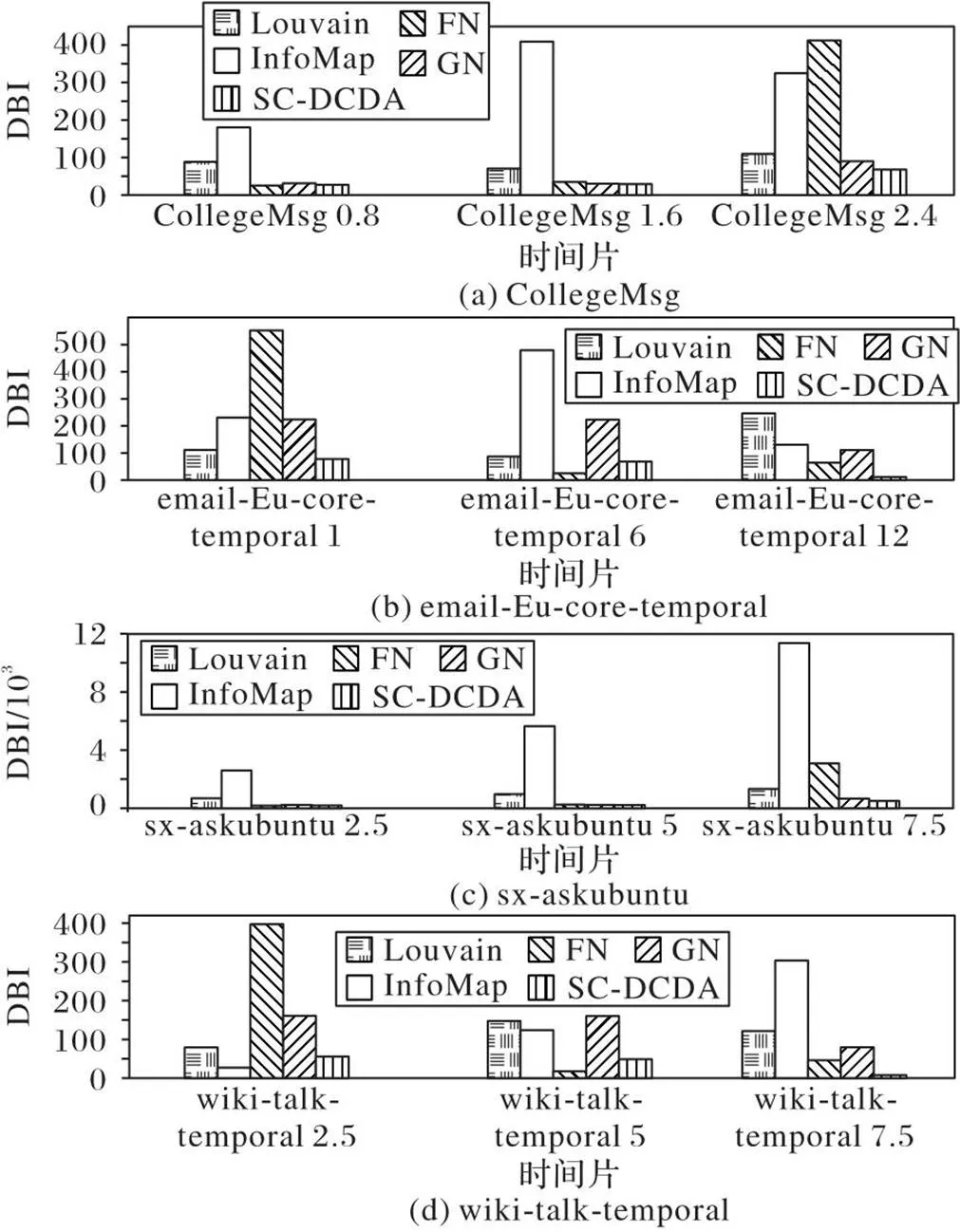
图7　SC-DCDA与典型算法的DBI对比

5 结语

本文基于动态社区结构演化，研究社交网络动态社区结构演化规律和动态数据集随时间变化的社区发现规律，侧重于演化事件中的出生事件、死亡事件、分裂事件和合并事件。采用真实数据集实验验证SC-DCDA的信息交互、聚类效果和准确度，结果显示SC-DCDA在动态数据集上的模块度得分、轮廓系数、CH指标和DBI较好。SC-DCDA为动态性、多样性和复杂性社交网络演化和结构分析提供研究方法和一定的参考价值；但该模型的抽象建模依赖于具体的领域场景和相似度的优化，是目前研究领域的局限和不足，也是下一步研究的方向。

动态社区发现只考虑社交网络的结构，忽略节点的属性特征，但节点属性对精准的社区发现更具有价值。未来将考虑节点在不同领域场景、不同时间片下属性的相似性，挖掘更多社区信息提高社区发现的精确度。此外，动态社区事件演化预测方面也需要进一步研究，主要体现在研究事件状态随时间片状态的迁移追踪的精确度：一方面需改进计算特征值和特征向量的算法，提高计算的效率；另一方面可以借助卷积神经网络历史信息前一时间片的信息和当前时间片信息去计算当前状态，模型上可借助注意力机制Attention做并行，观测时间片状态的迁移和研究事件收敛的关联度。

[1] PANZARASA P， OPSAHL T， CARLEY K M. Patterns and dynamics of users' behavior and interaction： network analysis of an online community［J］. Journal of the American Society for Information Science and Technology， 2009， 60（5）： 911-932.

[2] PARANJAPE A， BENSON A R， LESKOVEC J. Motifs in temporal networks［C］// Proceedings of the 10th ACM International Conference on Web Search and Data Mining. New York： ACM， 2017： 601-610.

[3] LI W， ZHONG K， WANG J， et al. A dynamic algorithm based on cohesive entropy for influence maximization in social networks［J］. Expert Systems with Applications， 2021， 169： No.114207.

[4] YIN Y， ZHAO Y， LI H， et al. Multi-objective evolutionary clustering for large-scale dynamic community detection［J］. Information Sciences， 2021， 549： 269-287.

[5] WANG Z， WANG C， LI X， et al. Evolutionary Markov dynamics for network community detection［J］. IEEE Transactions on Knowledge and Data Engineering， 2022， 34（3）： 1206-1220.

[6] BESHARATNIA F， TALEBPOUR A， ALIAKBARY S. An improved grey wolves optimization algorithm for dynamic community detection and data clustering［J］. Applied Artificial Intelligence， 2022， 36（1）： No.2012000.

[7] LI Y， HE K， BINDEL D， et al. Overlapping community detection via local spectral clustering［EB/OL］. （2015-09-26） ［2022-09-10］.https：//arxiv.org/pdf/1509.07996.pdf.

[8] WHARRIE S， AZIZI L， ALTMANN E G. Micro-， meso-， macroscales： the effect of triangles on communities in networks［J］. Physical Review E， 2019， 100（2）： No.022315.

[9] MUCHA P J， RICHARDSON T， MACON K， et al. Community structure in time-dependent， multiscale， and multiplex networks［J］. Science， 2010， 328（5980）： 876-878.

[10] PALLA G， BARABÁSI A L， VICSEK T. Quantifying social group evolution［J］. Nature， 2007， 446（7136）： 664-667.

[11] KANAVOS A， VOUTOS Y， GRIVOKOSTOPOULOU F， et al. Evaluating methods for efficient community detection in social networks［J］. Information， 2022， 13（5）： No.209.

[12] LI N， PEN M， JIANG W， et al. A community detection algorithm based on multi-similarity method［J］. Cluster Computing， 2019， 22（S2）： 2865-2874.

[13] QIN X， DAI W， JIAO P， et al. A multi-similarity spectral clustering method for community detection in dynamic networks［J］. Scientific Reports， 2016， 6： No.31454.

[14] CHEN J， WANG H， WANG L， et al. A dynamic evolutionary clustering perspective： community detection in signed networks by reconstructing neighbor sets［J］. Physica A： Statistical Mechanics and its Applications， 2016， 447： 482-492.

[15] OLSZEWSKI D. A clustering-based adaptive neighborhood retrieval visualizer［J］. Neural Networks， 2021， 140： 247-260.

[16] GUIDI B， MICHIENZI A， ROSSETTI G. Towards the dynamic community discovery in decentralized online social networks［J］ Grid Computing， 2019， 17（1）： 23-44.

[17] MOHAMMADMOSAFERI K K， NADERI H. Evolution of communities in dynamic social networks： an efficient map-based approach［J］. Expert Systems with Applications， 2020， 147： No.113221.

[18] IZAKIAN H， ABRAHAM A. Fuzzy C-means and fuzzy swarm for fuzzy clustering problem［J］. Expert Systems with Applications， 2011， 38（3）：1835-1838.

[19] BOUDEBZA S. An approach for detecting dynamic communities in social networks［D］. Jijel： Université Mohammed Seddik BenYahia， 2022： 1-165.

[20] TAKAFFOLI M， SANGI F， FAGNAN J， et al. Community evolution mining in dynamic social networks［J］. Procedia — Social and Behavioral Sciences， 2011， 22：49-58.

[21] ŠKRLJ B， KRALJ J， LAVRAČ N. Embedding-based Silhouette community detection［J］. Machine Learning， 2020， 109（11）： 2161-2193.

[22] 蒲实，赵卫东. 一种面向动态科研网络的社区检测算法［J］. 计算机科学， 2022， 49（1）：89-94.（PU S， ZHAO W D. Community detection algorithm for dynamic research network［J］. Computer Science， 2022， 49（1）：89-94.）

[23] 许平华，胡文斌，邱振宇，等. 节点不对称转移概率的网络社区发现算法［J］. 软件学报， 2019， 30（12）：3829-3845.（XU P H， HU W B， QIU Z Y， et al. Community detection algorithm based on asymmetric transition probability of nodes［J］. Journal of Software， 2019， 30（12）： 3829-3845.）

[24] 周锐，王桂娟，邓皓天，等. 复杂网络聚类特征层次布局算法［J］. 计算机应用研究， 2022， 39（2）：479-484.（ZHOU R， WANG G J， DENG H T， et al. Complex network clustering feature multi-level layout algorithm［J］. Application Research of Computers， 2022， 39（2）： 479-484.）

Spectral clustering based dynamic community discovery algorithm in social network

YANG Yu*， DUAN Weiwei

（，，611731，）

Dynamic community discovery is an important research area in Social Network Analysis （SNA）. As nodes joining or leaving social networks， the relationships between nodes establish or terminate， which affects community structure changes. The discovery algorithms of static communities in social networks lack of the essential historical information of community nodes， resulting in the insufficient network structure analysis as well as clustering information and the high computational cost. Aiming at these problems， based on the division of the community network evolution events， according to the analysis of the major community events， a Spectral Clustering based Dynamic Community Discovery Algorithm （SC-DCDA） was proposed. Firstly， according to the experimental observation， the dimensionality of high-dimensional data was reduced by using the method of spectral mapping. At the same time， the improved Fuzzy C-Means clustering （FCM） algorithm was adopted to determine the correlation between the nodes in the dynamic social network and the communities to be discovered. Secondly， the community structures were analyzed according to the evolutionary similarity matrix. Finally， the real network datasets and community discovery algorithm indicators， such as modularity score and Silhouette coefficient， were used to evaluate the effects of the proposed algorithm. Experimental results show that the computational cost of SC-DCDA is reduced by 8.37% compared with traditional spectral clustering， the average modularity score of the algorithm on all datasets is 0.49， and the qualitative analysis results of other algorithm metrics are also good， indicating that the proposed algorithm performs well in information interaction， clustering effect， and accuracy.

Social Network Analysis (SNA); dynamic community discovery algorithm; Fuzzy C-Means clustering (FCM); evolutionary similarity matrix

This work is partially supported by Science Research Fund Project of Department of Education of Yunnan Province （2020J1110）.

YANG Yu， born in 1988， Ph. D. candidate. His research interests include community discovery， network and system security.

DUAN Weiwei， born in 1998， M. S. candidate. His research interests include machine learning， deep learning， community detection.

1001-9081（2023）10-3129-07

10.11772/j.issn.1001-9081.2022101517

2022⁃10⁃14；

2023⁃01⁃03；

云南省教育厅科学研究基金资助项目（2020J1110）。

杨煜（1988—），男，安徽太和人，博士研究生，主要研究方向：社区发现、网络与系统安全； 段威威（1998—），男，安徽界首人，硕士研究生，主要研究方向：机器学习、深度学习、社区检测。

TP181

A

2023⁃01⁃10。