基于协方差矩阵自适应进化策略的机器人手眼标定算法

赵云涛，谢万琪，李维刚，胡佳明

基于协方差矩阵自适应进化策略的机器人手眼标定算法

赵云涛1，2，谢万琪2*，李维刚1，2，胡佳明2

（1.冶金自动化与检测技术教育部工程研究中心（武汉科技大学），武汉 430081； 2.武汉科技大学 信息科学与工程学院， 武汉 430081）（ ∗ 通信作者电子邮箱atolrop@163.com）

针对视觉传感器标定和机器人运动学求解过程中存在噪声干扰，导致传统的手眼标定算法求解误差较大的问题，提出一种基于协方差矩阵自适应进化策略（CMAES）的机器人手眼标定算法。首先，采用对偶四元数（DQ）对旋转和平移分别建立目标函数和几何约束，简化求解模型；其次，采用惩罚函数法将约束问题转化成无约束优化问题；最后，使用CMAES算法逼近手眼标定旋转和平移方程的全局最优解。搭建机器人、相机实测实验平台，将所提算法与Tsai两步法、非线性优化算法INRIA、DQ算法进行对比。实验结果表明：所提算法在旋转和平移上的求解误差和方差均小于传统算法；与Tsai算法相比，所提算法的旋转精度提升了4.58%，平移精度提升了10.54%。可见在存在噪声干扰的实际手眼标定过程中，所提算法具有更好的求解精度与稳定性。

机器人；协方差矩阵自适应进化策略；对偶四元数；手眼标定；约束优化

0 引言

手眼标定用于获取机器人坐标系和视觉传感器坐标系之间的齐次变换矩阵，将相机拍摄到物体在世界坐标系的位姿信息转换成在机器人基坐标系下的空间坐标，从而实现机器人对目标的抓取、点焊等操作。

此后，Tsai等［2］提出了手眼标定算法，给出了该方法下手眼标定数据集的筛选原则，并采取线性的方法分两步先求解出旋转矩阵，再根据旋转矩阵求解出平移向量；Park等［3］提出Navy手眼标定算法，通过使用李群理论的知识求解手眼标定经典方程；Daniilidis等［4］提出了对偶四元数（Dual Quaternion， DQ）方法。

以上方法虽然采用了不同的数学工具，但都有相同的特点：旋转和平移的解是用线性代数的方法估计的。这些方法在理想的仿真环境下能获得高精度的求解结果，但在实际的手眼标定过程中，相机标定和机器人运动学求解过程会存在一些噪声，允许线性化旋转方程的几何性质在有噪声的情况下不成立，需要解决的线性问题是病态的，最后导致了方程求解的非线性和不稳定性。

Dornaika等［5］提出INRIA算法，用非线性优化方法同时求解旋转和平移矩阵，相较于以往的算法精度有所提升；王君臣等［6］也采用了非线性的方法，将手眼标定问题转化为一个非线性优化问题。但是手眼校准本质上是非凸的，因此任何封闭形式的解都只是一个近似的答案，求解过程中可能落入局部最优，对求解时的初值有较高要求。

在近期的手眼标定算法研究中，一些方法采用了全局优化的思想：文献［7］中首次采用了全局思想研究手眼标定问题；文献［8］在文献［7］的基础上采用了最小二乘法进行全局迭代；文献［9-10］中采用凸松弛优化方法解决手眼标定的问题，通过gloptipoly3工具箱将非凸问题转换为凸优化问题，相比传统解法具有更高的求解精度和稳定性。但这类方法依赖于问题参数模型的选取，对于大规模问题通常不是很实用，因为凸松弛的计算代价是解决单个凸问题的倍数［11］。

协方差矩阵自适应进化策略（Covariance Matrix Adaptation Evolutionary Strategy， CMAES）是在进化策略（Evolutionary Strategy， ES）算法的基础上发展起来的一种新型无约束的全局优化方法，文献［12］中将它成功应用在标定领域，验证了该算法有很好的搜索性能。与遗传算法（Genetic Algorithm， GA）、粒子群优化（Particle Swarm Optimization， PSO）算法相比，它的收敛更快且搜索精度更高。本文在上述研究的基础上将CMAES算法应用于对偶四元数手眼标定方程的求解，主要有以下改进：

1）使用对偶四元数分别建立旋转和平移的目标函数和几何约束，简化求解问题模型，用CMAES算法替代传统对偶四元数中的奇异值分解算法，减小旋转和平移误差。

2）采用CMAES算法求解手眼标定方程，不对手眼标定的非凸问题进行松弛处理而是直接解决，相较于文献［9-10］中的算法，求解更快。

3）通过惩罚函数法［13］对手眼标定的约束条件进行迭代，将约束优化问题转化为无约束优化问题，从而通过CMAES算法逼近手眼标定方程的全局最优值。

最后，搭建机器人、相机实测实验平台，将本文算法与三种传统算法（Tsai、INRIA、DQ）进行对比，验证了本文算法在存在噪声干扰的实际手眼标定过程中，旋转和平移的求解误差和方差均小于其他算法，具有更好的求解精度与稳定性。

1 手眼标定问题

手眼标定的目的是求取机器人执行器末端到相机传感器的齐次变换矩阵，通过多次变换机器人末端位置，拍摄不同角度的标定板图片，作为手眼标定的参数。其中一次手眼标定如图1所示。

如图1所示，本文的手眼标定系统采用手在眼上（Eye-in-hand）的安装方式，用表示两次机器人运动末端相对位置的转换矩阵；表示两次相机相对位置的转换矩阵；是机器人末端到相机的转换矩阵。手眼标定的数学模型是：

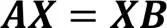
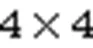
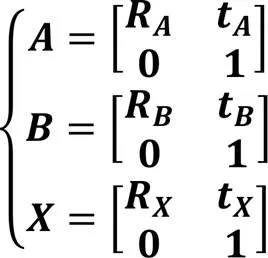
将式（2）的齐次变换矩阵代入式（1）展开，可以得到手眼标定问题的初始数学模型：

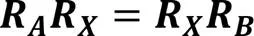
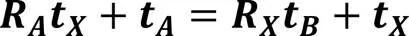
由于的求解需要两组观测值，所以机器人至少得变换3个不同位置进行相机拍摄。在实际求解中，通过对机器人进行次位姿变换，得到组和，求解矩阵方程组：

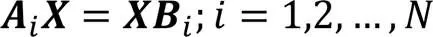
其中：，、为两次不同运动的机器人末端坐标位置，可以通过机器人运动学正解求得；，、则是标定板的两次运动视觉传感器所对应的外参矩阵，可以通过张正友标定法得到。

2 AX=XB方程的对偶四元数模型

2.1　对偶四元数的性质

对偶四元数（DQ）是对偶数和四元数在多维空间中的结合，本文采用DQ表示空间的任意旋转和平移，可以避免万向节死锁的问题。DQ的数学形式如下：

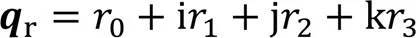
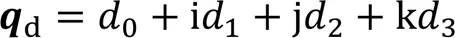
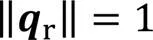
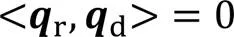
2.2　手眼标定的对偶四元数模型

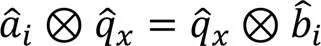
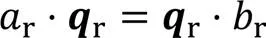
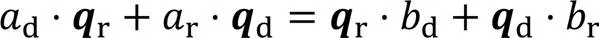
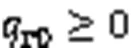
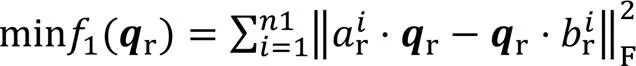
其中1表示手眼标定进行的姿态变换次数。

以式（15）建立DQ平移部分的优化方程，并以单位DQ的性质式（10）建立约束条件，建立平移问题模型：

根据四元数乘法的性质（式（12）），可以简化式（17）的平移方程：

列出简化后平移部分的优化问题模型2：

3 基于CMAES的手眼标定算法

3.1　CMAES

CMAES采用择优截断选择策略，能防止手眼标定问题模型的种群过早收敛；在有噪声的实际标定环境中，能减少因噪声干扰导致求解模型陷入局部最优的情况［14］。本文采用CMAES逼近手眼标定旋转和平移方程的全局最优解，对目标进行采样并更新迭代进化路线，直到搜索到满意的解或达到最大迭代次数［15］。

1）进行采样与最优子群计算。

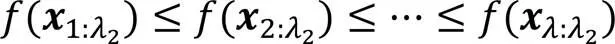
2）更新均值。

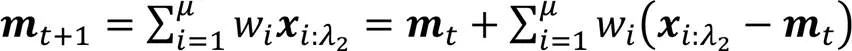
3）协方差矩阵自适应调整。

协方差矩阵的更新路径和协方差更新公式分别如式（22）～（23）所示：

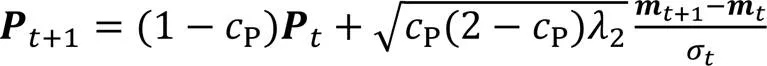
4）步长调整。

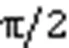
步长进化路径的公式为：

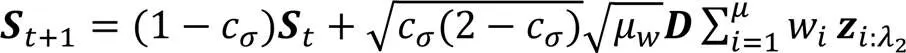
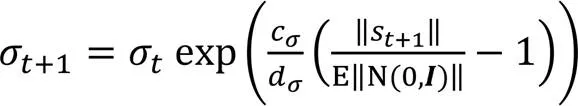
3.2　惩罚函数法转换约束条件

由于CMAES算法适用于无约束优化，为了方便优化模型的求解，本文引入了惩罚函数法。利用适当定义的复合函数再在原目标函数上建立惩罚函数法，把有约束的优化问题转换为无约束优化问题再加以解决，并通过定义可达性指数为手眼标定方程优化问题模型中的停止判断条件：

针对本文的约束问题：

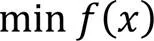
构造辅助函数如下：

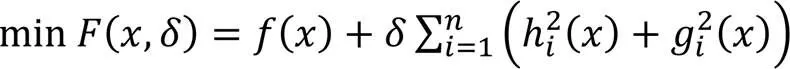
根据式（27），将式（16）的约束条件进行转换，构造新的旋转优化模型如下：

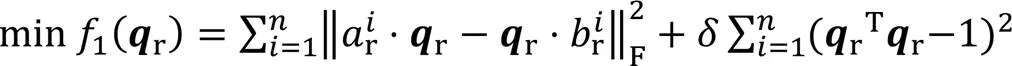
求解旋转部分的优化方程后，再根据式（18）、式（27）构造DQ平移部分手眼标定优化模型：

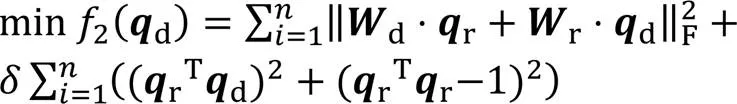
3.3　基于CMAES的手眼标定算法设计

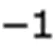
步骤3 建立优化模型，见式（28），使用采样的候选解计算优化问题函数值；并按式（20）排序，组成当前最优子群。

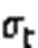
当满足停止条件并成功获取旋转模型的解后，将步骤3的优化模型（式（28））替换成平移优化模型（式（29）），重复步骤1～7，获取平移模型的解，最后将DQ转换为手眼标定齐次变换矩阵进行输出。

4 实验与结果分析

实验采用Eye-in-hand手眼标定系统与HM06型号机器人，重复精度在0.05 mm以内，搭载Azure Kinect相机传感器，RGB相机的分辨率为3 840×2 160，标定板采用8×11的棋盘格标准，单个棋盘格的边长为15 mm，实验场景如图2所示。

实验环境为Windows 11 64位操作系统，Intel Core i5-8300H CPU 2.30 GHz，RAM 8.0 GB。

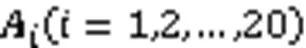
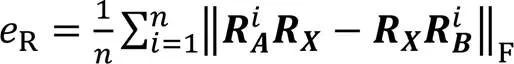
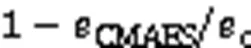
图3（a）和表1反映了在10组测试实验中，本文算法在求解手眼标定旋转部分的误差平均值最小，旋转误差最大值为1.128 5°，最小为0.552 0°。在各组算法中，本文算法的旋转误差的方差最小，说明它的优化结果更稳定。与经典手眼标定算法相比，本文算法的精度均有提升，旋转精度比Tsai提升了4.58%，最高提升了10.60%。

图3　四种算法的旋转误差与平移误差

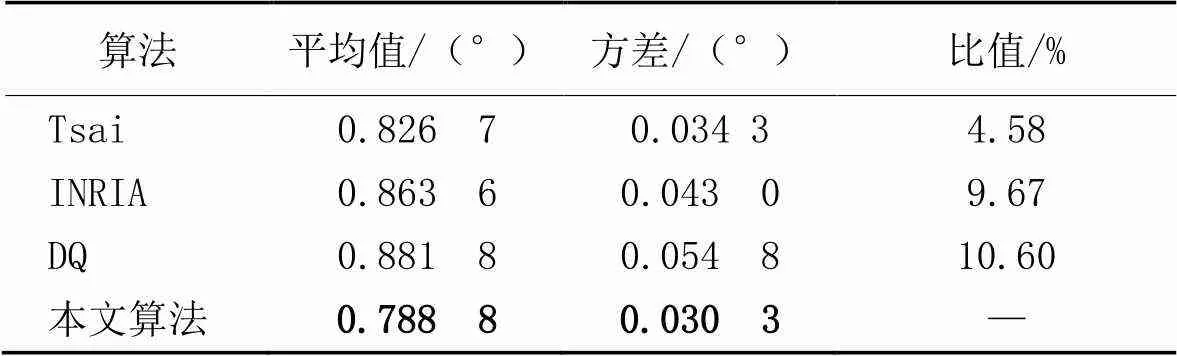
表1　旋转误差数据对比

通过图3（b）、表2可以看出，本文算法在4种算法里方差最小，说明全局优化算法在寻优过程中更稳定，旋转精度和平移精度都有所提升。由于实际实验的噪声干扰，传统手眼标定的线性方法在平移矩阵的求解过程受到的影响更大，因此本文算法相较于其他传统算法有了更大的提升，与Tsai相比，平移精度提高了10.54%。不足的是，传统算法的求解时间均在0.2 s内，而本文算法采用择优截断选择策略，牺牲了一部分求解效率，10次手眼标定平均求解时间为0.593 s，比传统算法稍长。

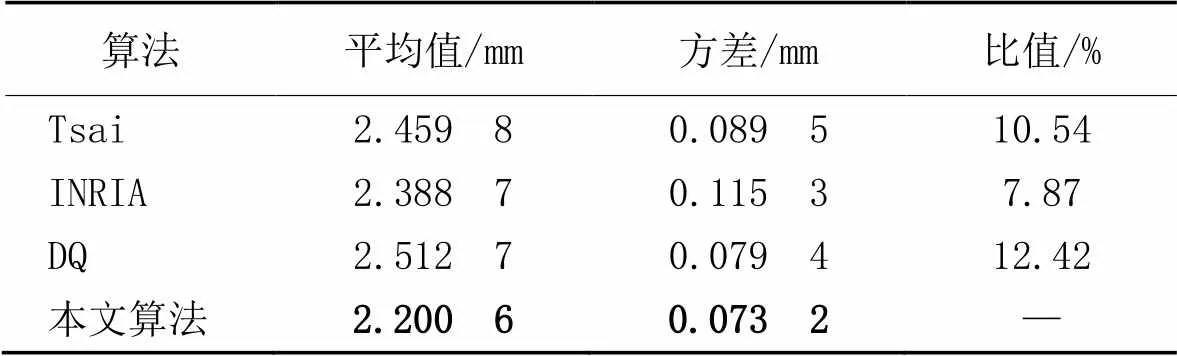
表2　平移误差数据对比

5 结语

本文提出基于CMAES的手眼标定算法，将协方差矩阵自适应进化策略应用于全局优化过程，在实际手眼标定过程中减少了噪声的影响，更大程度避免了齐次方程=的求解落入局部最优的问题。在求解过程中采用数学工具对偶四元数，使用惩罚函数法转化约束问题，方便手眼标定方程的求解，最后使用CMAES分别求解旋转和平移部分。实验结果表明，本文算法的平移误差和旋转误差的方差最小，验证了算法寻优效果的稳定性，并且精度较传统算法有所提高，在机器人视觉系统的应用中具有一定的潜力。

[1] SHIU Y C， AHMAD S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB［J］. IEEE Transactions on Robotics and Automation， 1989， 5（1）： 16-29.

[2] TSAI R Y， LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration［J］. IEEE Transactions on Robotics and Automation， 1989， 5（3）： 345-358.

[3] PARK F C， MARTIN B J. Robot sensor calibration： solving AX=XB on the Euclidean group［J］. IEEE Transactions on Robotics and Automation， 1994， 10（5）： 717-721.

[4] DANIILIDIS K， BAYRO-CORROCHANO E. The dual quaternion approach to hand-eye calibration［C］// Proceedings of 13th International Conference on Pattern Recognition — Volume 1. Piscataway： IEEE， 1996： 318-322.

[5] DORNAIKA F， HORAUD R. Simultaneous robot-world and hand-eye calibration［J］. IEEE Transactions on Robotics and Automation， 1998， 14（4）： 617-622.

[6] 王君臣，王田苗，杨艳，等. 非线性最优机器人手眼标定［J］. 西安交通大学学报， 2011， 45（9）： 15-20， 89.（WANG J C， WANG T M， YANG Y， et al. Nonlinear optimal robot hand-eye calibration［J］ Journal of Xi’an Jiaotong University， 2011， 45（9）： 15-20， 89.）

[7] HELLER J， HENRION D， PAJDLA T. Hand-eye and robot-world calibration by global polynomial optimization［C］// Proceedings of the 2014 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2014： 3157-3164.

[8] 王一凡，段锁林，高仁洲，等. 基于对偶四元数的机器人手眼标定算法研究［J］. 机电工程， 2019， 36（7）： 755-760， 765.（WANG Y F， DUAN S L， GAO R Z， et al. Study on robot hand-eye calibration using dual quaternion［J］. Journal of Mechanical and Electrical Engineering， 2019， 36（7）： 755-760， 765.）

[9] 李巍，吕乃光，董明利，等. 凸松弛全局优化机器人手眼标定［J］. 计算机应用， 2017， 37（5）： 1451-1455.（LI W， LYU N G， DONG M L， et al. Robot hand-eye calibration by convex relaxation global optimization［J］. Journal of Computer Applications， 2017， 37（5）： 1451-1455.）

[10] 王龙，闵华松. 基于LMI优化的对偶四元数手眼标定算法［J］. 机床与液压， 2021， 49（21）：8-14.（WANG L， MIN H S. Dual quaternion hand-eye calibration algorithm based on LMI optimization［J］. Machine Tools and Hydraulics， 2021， 49（21）： 8-14.）

[11] GONG P H， ZHANG C S， LU Z S， et al. A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems［C］// Proceedings of the 30th International Conference on Machine Learning. New York： JMLR.org， 2013： 37-45.

[12] 仲志丹，张玮琪，杜慧颖. 基于CMAES算法的加速度计多位置新型标定方法［J］. 智能计算机与应用， 2018， 8（2）： 30-34.（ZHONG Z D， ZHANG W Q， DU H Y. New multi-position calibration method for accelerometer based on CMAES algorithm［J］. Intelligent Computer and Applications， 2018， 8（2）： 30-34.）

[13] 曾繁琦，袁晓静，王旭平，等. 基于荷电状态惩罚函数的能量管理策略优化方法［J］. 中国机械工程， 2022， 33（7）： 852-587， 871.（ZENG F Q， YUAN X J， WANG X P， et al. Energy management strategy optimization method based on SOC penalty function［J］. China Mechanical Engineering， 2022， 33（7）： 852-587， 871.）

[14] 黄亚飞，梁昔明，陈义雄. 求解全局优化问题的正交协方差矩阵自适应进化策略算法［J］. 计算机应用， 2012， 32（4）：981-985.（HUANG Y F， LIANG X M， CHEN Y X. Hybrid orthogonal CMAES for solving global optimization problems［J］. Journal of Computer Applications， 2012， 32（4）： 981-985.）

[15] WANG T C， TING C K. Fitness inheritance assisted MOEA/D-CMAES for complex multi-objective optimization problems［C］// Proceedings of the 2018 IEEE Congress on Evolutionary Computation. Piscataway： IEEE， 2018： 1-8.

[16] 陈兴国，徐修颖，陈康扬，等. 基于CMAES集成学习方法的地表水质分类［J］. 计算机科学与探索， 2020， 14（3）：426-436.（CHEN X G， XU X Y， CHEN K Y， et al. Surface water quality classification via CMAES ensemble method［J］. Journal of Frontiers of Computer Science and Technology， 2020， 14（3）： 426-436.）

[17] ENEBUSE I， FOO M， IBRAHIM B S K K， et al. A comparative review of hand-eye calibration techniques for vision guided robots［J］. IEEE Access， 2021， 9： 113143-113155.

[18] DEKEL A， HÄRENSTAM-NIELSEN L， CACCAMO S. Optimal least-squares solution to the hand-eye calibration problem［C］// Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2020： 13595-13603.

Robot hand-eye calibration algorithm based on covariance matrix adaptation evolutionary strategy

ZHAO Yuntao1，2， XIE Wanqi2*， LI Weigang1，2， HU Jiaming2

（1，（），430081，；2，，430081，）

To solve the problem that the traditional hand-eye calibration algorithms have large solution errors due to the noise interference in the processes of vision sensor calibration and robot kinematics solution， a robot hand-eye calibration algorithm based on Covariance Matrix Adaptation Evolutionary Strategy （CMAES） was proposed. Firstly， the mathematical tool Dual Quaternion （DQ） was used to establish the objective functions and geometric constraints for both rotation and translation， and the solution model was simplified. Then， the penalty function method was used to transform the constrained problem into an unconstrained optimization problem. Finally， CMAES algorithm was used to approximate the global optimal solution of hand-eye calibration rotation and translation equations. An experimental platform of robot and camera measurement was built， and the proposed algorithm was compared with two-step Tsai algorithm， the nonlinear optimization algorithm INRIA， and the DQ algorithm. Experimental results show that the solution error and variance of the proposed algorithm are smaller than those of traditional algorithms for both rotation and translation. Compared with Tsai algorithm， the proposed algorithm has the rotation accuracy improved by 4.58%， and the translation accuracy improved by 10.54%. It can be seen that the proposed algorithm has better solution accuracy and stability in the actual hand-eye calibration process with noise interference.

robot; Covariance Matrix Adaptation Evolutionary Strategy (CMAES); Dual Quaternion (DQ); hand-eye calibration; constrained optimization

1001-9081（2023）10-3225-05

10.11772/j.issn.1001-9081.2022081282

2022⁃09⁃19；

2022⁃11⁃10；

湖北省教育厅科学技术研究计划项目（B2020012）。

赵云涛（1982—），男，内蒙古赤峰人，副教授，博士，主要研究方向：机器视觉、机器人应用； 谢万琪（1998—），男，湖北武汉人，硕士研究生，主要研究方向：机器人与视觉、点云； 李维刚（1977—），男，湖北咸宁人，教授，博士，主要研究方向：智能优化、数据挖掘； 胡佳明（1998—），男，湖北鄂州人，硕士研究生，主要研究方向：智能优化、机器人控制。

TP242

A

2022⁃11⁃25。

This work is partially supported by Science and Technology Research Program of Department of Education of Hubei Province （B2020012）.

ZHAO Yuntao， born in 1982， Ph. D.， associate professor. His research interests include machine vision， robot application.

XIE Wanqi， born in 1998， M. S. candidate. His research interests include robot and vision， point cloud.

LI Weigang， born in 1977， Ph. D.， professor. His research interests include intelligent optimization， data mining.

HU Jiaming， born in 1998， M. S. candidate. His research interests include intelligent optimization， robot control.