基于节点相似性分组与图压缩的图摘要算法

宏宇，陈鸿昶，张建朋*，黄瑞阳

基于节点相似性分组与图压缩的图摘要算法

宏宇1，陈鸿昶2，张建朋2*，黄瑞阳2

（1.郑州大学 网络空间安全学院，郑州 450002； 2.信息工程大学 信息技术研究所，郑州 450002）（ ∗ 通信作者电子邮箱j_zhang_edu@sina.com）

针对当前图摘要方法压缩率较高，图压缩算法无法直接被用于下游任务分析的问题，提出一种图摘要与图压缩的融合算法，即基于节点相似性分组与图压缩的图摘要算法（GSNSC）。首先，初始化节点为超节点，并根据相似度对超节点分组；其次，将每个组的超节点合并，直到达到指定次数或指定节点数；再次，在超节点之间添加超边和校正边以恢复原始图；最后，对于图压缩部分，判断对每个超节点的邻接边压缩和摘要的代价，并选择二者中代价较小的执行。在Web-NotreDame、Web-Google和Web-Berkstan等6个数据集上进行了图压缩率和图查询实验。实验结果表明，在6个数据集上，与SLUGGER（Scalable Lossless sUmmarization of Graphs with HiERarchy）算法相比，所提算法的压缩率至少降低了23个百分点；与SWeG（Summarization of Web-scale Graphs）算法相比，所提算法的压缩率至少降低了13个百分点；在Web-NotreDame数据集上，所提算法的度误差比SWeG降低了41.6%。以上验证了所提算法具有更好的图压缩率和图查询准确度。

图摘要；图压缩；图查询；超边；最小描述长度

0 引言

图数据可以用于建模实体和实体之间的复杂关系，在现实世界中应用广泛，如社交网络、蛋白质分子网络、合作关系网络和通信网络等。许多计算问题都可以转换成图上的计算问题，从而利用图上的相关技术解决问题。图有很多下游任务，如模式挖掘、社区发现、图查询和可视化等，服务于解决现实问题；然而，随着数据规模的爆炸式增长，用于分析的图数据也越来越复杂多样，难以存储和分析，解决这些问题已经成为当前研究的热点和难点。

目前用于解决图数据量大问题的技术包括图压缩和图摘要（Graph summarization）技术。图摘要技术［1-11］将具有较高相似度的节点合并成超节点，减少节点和边的数量以降低图的复杂度，主要方法有基于节点分组的方法［5-7］、基于边分组的方法［2］和基于稀疏化的方法［1］等。图压缩技术［4，12-16］将图数据以存储占用更低的压缩方式存储，主要方法有基于顶点重排序的方法［12-13］和基于邻接矩阵的方法［14］等。这两类技术的侧重点不同，图摘要技术侧重于保存图的结构信息，它的输出是一个更为抽象紧凑的图，因此可以直接用于下游任务分析；图压缩技术则是以各种方式最大限度地降低图数据在磁盘空间或内存空间的存储占用，由于图压缩技术并不关注图的结构信息，因此在降低存储空间方面，图压缩效果更好，但是图压缩产生的图并不能直接使用，需要先对压缩后的图进行解码操作。

通过对比两种技术的特点可以发现，图摘要虽然能够降低图的复杂度，但为了能够恢复原始图和保存结构特征，它的效果比图压缩的效果差；而图压缩虽然能够更好地降低图的消耗，但是不能直接用于分析。

针对以上问题，本文提出一种基于节点相似性分组与图压缩的图摘要算法（Graph Summarization algorithm based on Node Similarity grouping and graph Compression， GSNSC），结合了图摘要与图压缩的优势。

本文的主要工作如下：

1）提出了一种基于节点相似性分组与图压缩的图摘要算法（GSNSC）。首先通过将节点分组聚合成超节点的方式产生较小的输出摘要图，其次压缩摘要图中的超边和校正边，降低图的压缩率，减少运行时间。所提算法不仅能够降低图的存储空间占用，而且还能直接用于挖掘和分析。

2）在真实数据集上进行实验，实验结果表明，所提算法比现有的图摘要算法具有更好的压缩率和更低的运行时间。针对图查询设计了相关实验，验证了所提算法具有较好的查询准确度。

1 相关工作

1.1　图摘要

图摘要又叫作图概要，是一种降低大规模图的复杂度和描述长度的技术。它通过一些策略（如合并多个节点成一个超节点、去掉不重要的边等）创建一个摘要图，在降低图的成本的同时也保存了图的结构特征，使得到的摘要图能够更容易地支持图模式挖掘、可视化和邻域查询等下游任务。

图1　例子示意图

1.2　图压缩

图压缩也是降低图规模的一种方法，和图摘要的区别是它不关注图的结构信息和语义信息，它的目标是尽可能地降低图的存储空间占用，使得大图数据可以存储在较小的磁盘空间上，以解决图数据量较大的问题。目前图压缩的研究还处于起步阶段［4］，这些方法大多压缩节点的边，其中较为常用的是基于节点重排的方法。由于真实的图通常都是非常稀疏的，如在社交网络中，节点代表用户，边代表用户之间的好友关系，图中的节点数可能达到上千万甚至上亿，而每个节点的好友关系可能仅有几十或者几百条。图压缩可以在不改变图结构的情况下压缩节点的稀疏邻边，因此当使用邻接表压缩边时，节点的排序非常重要。通过节点重排算法可以更好地降低图的压缩率，每个节点的邻边以邻接表保存，其次利用编码技术压缩节点的邻边。可以看出，图压缩技术的目的是降低图数据的存储空间占用，并不保留图的结构特征，因此单纯的图压缩技术产生的压缩图不是图的结构，不能直接用于分析，必须进行解码操作。本文的目标不仅是降低图的存储空间占用，而且还能直接用于挖掘和分析，因此需要结合图摘要技术改进算法。

文献［14］中利用邻接矩阵的特征提出了2-tree，2-tree能很好地压缩邻接矩阵，实现较好的时间/空间均衡，但2-tree还面临以下问题：2-tree中还存在大量的同构子树；2-tree只能压缩稀疏图；2-tree只能表示静态图，不能向其中增加或者删除边。针对上述问题，文献［21］中把多值决策图（Multiple-valued Decision Diagram， MDD）和2-tree结合，提出了2-MDD，利用MDD的删除规则和化简规则合并相同子图。

2 问题定义

在本文研究中，创建摘要图采用最小描述长度（Minimum Description Length， MDL）原则［22］，MDL原则的目的是寻找最好的损失模型，使得模型和编码数据的损失最小。本文通过最小描述长度创建摘要图和压缩图，问题定义如下：

表1　符号及含义

3 算法基本原理

本文算法使用的代价模型分两部分组成，分别是对边进行图摘要方式存储的代价模型和对边进行图压缩方式存储的代价模型。对节点进行图摘要的损失如下：

压缩超节点相连的超边时的损失如下：

通过式（1）可以得出合并一对节点的收益为：

其中为合并和之后的节点。合并超节点对的收益表示相较于合并之前，合并之后图的总消耗的降低量，该值越大说明收益越高。

3.1　算法描述

2）合并阶段。合并第1）步产生的每个组。计算超节点的合并收益时需要查找所有其他超节点，选出最佳的那个超节点与之合并，但是这样会非常浪费时间，因此采取分组合并的方式降低时间复杂度。

首先根据超节点的shingle值（见3.2节）将超节点划分成多个组，每个组内的超节点都比较相似，即有很多个公共邻居，将这些节点合并会使得合并前后的总体边数量大幅降低。分组后只需要对每个组内的超节点计算合并收益，不必搜索整个超节点集，大幅缩小了查找范围。合并完成后，执行以下操作：

编码 将满足条件的超节点之间连接超边并更新校正边集，对于每个超节点的所有邻接超边，比较压缩存储或者摘要存储的消耗，选择存储消耗更小的方式存储。

GSNSC的伪代码如算法1所示。

算法1 GSNSC。

while（<） do

合并每个组

3.2　分组阶段

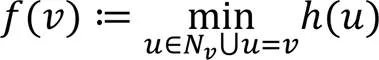
分组阶段的伪代码如算法2所示。

算法2 分组阶段。

3.3　合并阶段

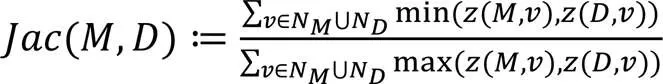
合并阶段的伪代码如算法3所示。

算法3 合并阶段。

while（||>1 &&<） do

随机采样中任意节点对

3.4　编码阶段

当处理所有超节点后，再压缩校正边集。具体步骤为：首先遍历原始图中的每一个节点，获取每一个节点的所有校正边，其次计算该节点的邻边压缩存储消耗和摘要存储消耗，如果压缩需要的存储代价更小，则选择压缩，以段的方式存储；否则以节点对的方式存储。至此算法结束，返回摘要压缩图和校正边集合。

编码阶段的伪代码如算法4所示。

算法4 编码阶段。

6） else

11） else

15） 压缩

17） else

3.5　算法时间复杂度分析

3.6　算法空间复杂度分析

4 实验与结果分析

4.1　实验设置

1）数据集。

实验使用的数据集如表2所示。Web-Berkstan数据集（http：//snap.stanford.edu/data/）中节点代表来自berkely.edu 和stanford.edu的页面，边代表它们之间的连接。类似地，Web-Google和Web-NotreDame数据集中的节点分别代表谷歌和诺特丹大学网站的页面。DBLP数据集中，节点代表论文作者，边代表两个作者之间有合作关系。Skitter数据集为Internet拓扑图，追踪路线从几个分散的来源到数百万个目的地。Youtube数据集为在线社交网络数据集。

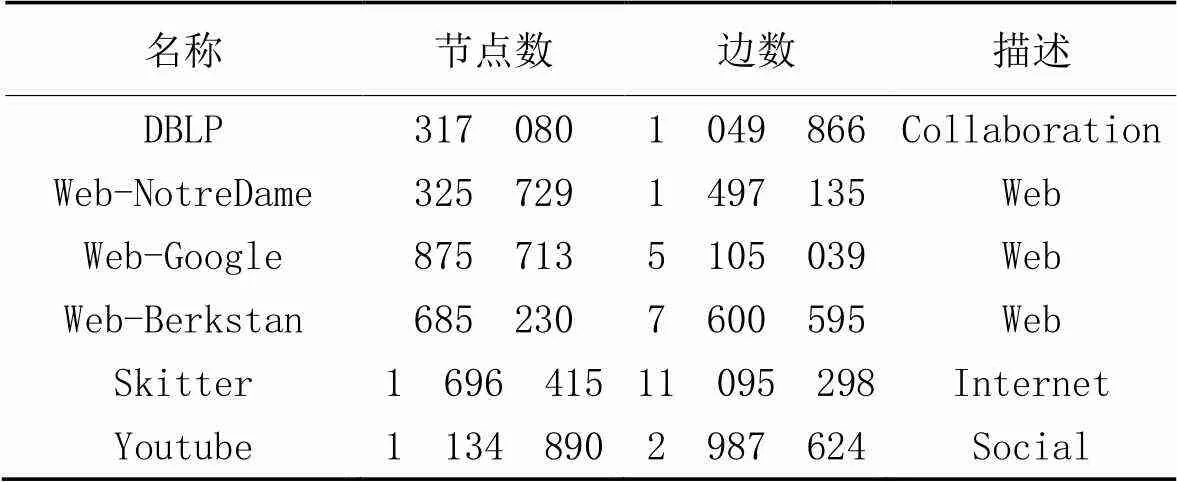
表2　数据集描述

2）环境设置。

GSNSC代码运行在一个Intel Xeon CPU E5-2650 v4 @ 2.20 GHz的linux服务器上，其中包含4个CPU，每个CPU12核，语言为C++。

3）评价指标。

4.2　对比算法

针对压缩率对比实验，对比算法如下。

1）DPGS［6］。原算法的损失函数是编码长度而不是边和节点的数量，实验中采用本文中的损失函数。

2）SWeG［5］。该算法采用和本文算法相同的分组方式，但是在合并步骤上有所不同。

3）GREEDY［3］。该算法是图摘要的经典贪心算法。

4）GreedyCS［4］。和本文算法类似，该算法也是采用图摘要和图压缩结合的方法降低图的规模。

5）SLUGGER［18］。该算法贪婪地将节点合并为超节点，同时维护和利用它们的层次结构。

4.3　压缩率和运行时间实验

不同算法的压缩率和运行时间实验结果对比如表3所示，其中：OOT代表运行时间太久或内存超过限制，属于无效数据；压缩率为输出图与输入图大小的比值，值越小，效果越好。设置阈值分别为0.1、0.2和0.3（SLUGGER无阈值区分），对比每种算法的实验结果。对于同一数据集的同一个方法，当越大时，效果越差，这是因为越大，合并节点的门槛就越高，节点越不容易被合并，因此输出图中的节点数和边数就越多，导致压缩率更高。与SLUGGER相比，GSNSC的压缩率至少降低了23个百分点；与SweG相比，压缩率至少降低了13个百分点。通过每个数据集上的结果可以看出，GSNSC的压缩率效果明显优于其他对比算法，原因是该算法相较于其他对比算法，不仅压缩摘要图中的超边，还压缩了用于恢复原图的校正边集，后者对压缩率降低做出最大贡献，这是因为校正边集通常总是远大于超边集，两个超节点之间最多有一条超边，但是可以有多条校正边。对于不同的数据集，同种方法压缩率相差较大；从结果可以看出，图的密度越低，压缩率就越好。

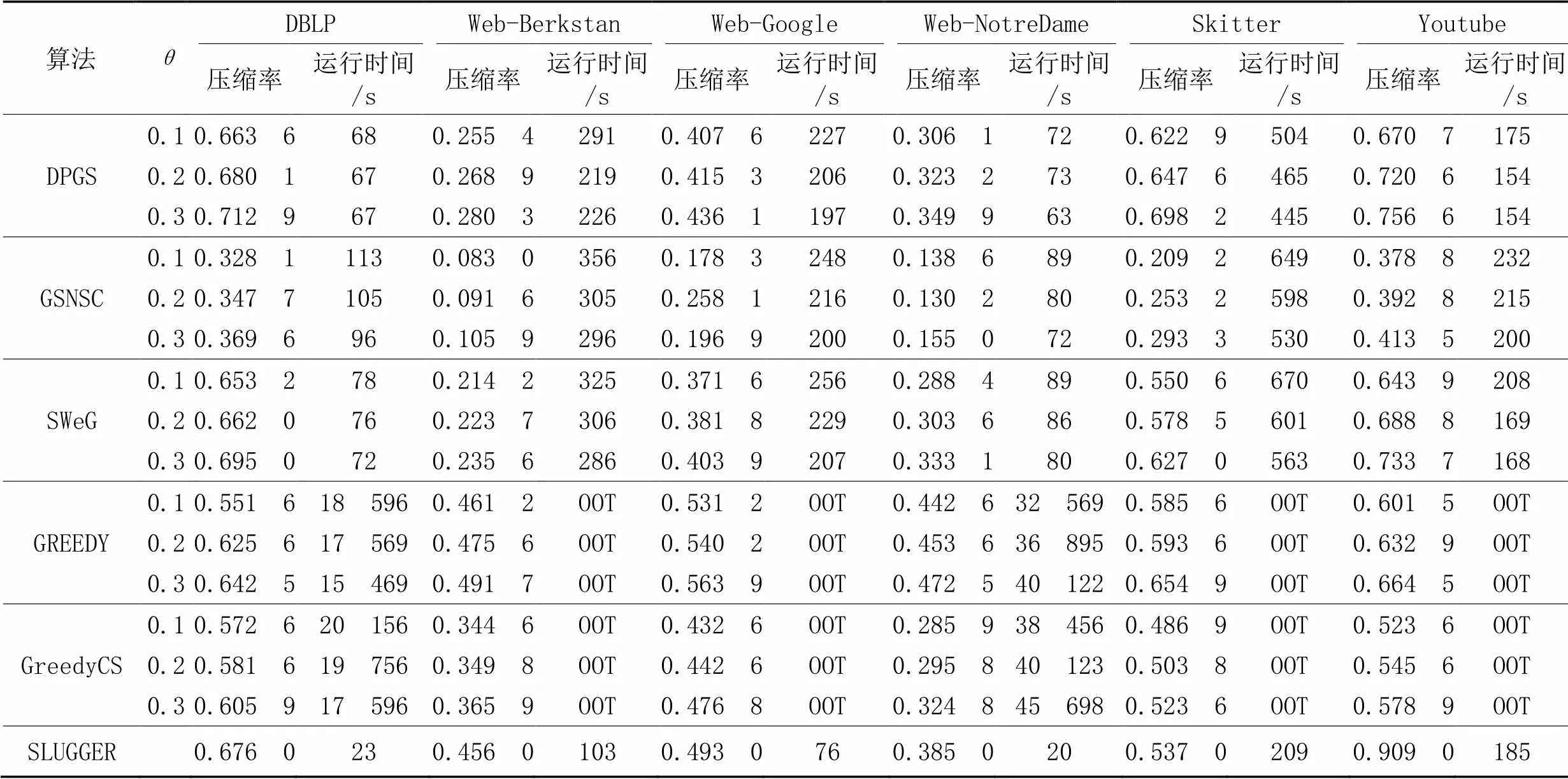
表3　不同算法在6个数据集上的实验结果对比

4.4　θ和压缩率的关系

图2展示了在Web-NotreDame数据集下测试的和压缩率之间的关系。可以看出，当值为0.05时压缩率最低，当值逐渐变大，压缩率也在不断升高；这是由于越大，节点合并的阈值就越高，因此效果越差。

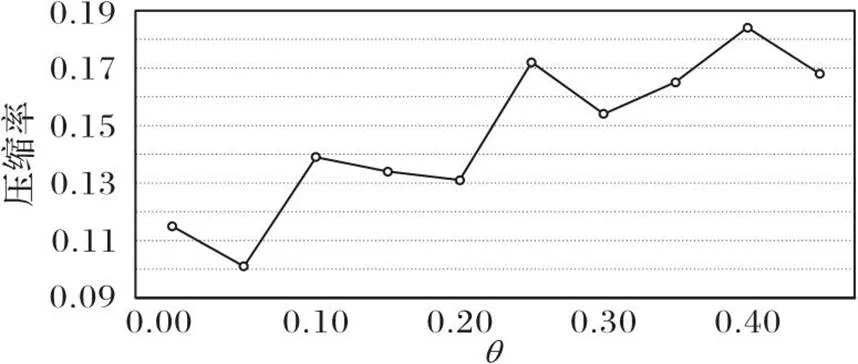
图2　Web-NotreDame数据集上和压缩率的关系

4.5　T和压缩率的关系

图3展示了在Web-NotreDame数据集上，当=0.2时迭代次数和压缩率之间关系的实验结果。可以看出，在的取值为1到5时，压缩率下降较快；这是由于此时太小，每次循环合并的节点数是有限的，因此每增加1，压缩率就大幅下降。当>5时，越往后压缩率不断上下浮动并趋于稳定，这很大程度上是由于算法运行具有随机性。

图3　Web-NotreDame数据集上T和压缩率的关系（θ=0.2）

4.6　图查询

通过期望邻接矩阵对图进行查询将会比在原始图上更快，这是因为摘要图中的节点数很少，因此邻接矩阵相较于原始图更小，因此查询效率更高，本文从图查询的准确度方面评估摘要图的好坏。

对比GSNSC、DPGS和SweG这3种算法在Web-NotreDame数据集上的度误差，在Web-NotreDame和Web-Google数据集上的邻接误差，实验结果如表4所示。可以看出，GSNSC的度误差和邻接误差更低，与SweG相比，度误差降低了41.6%，说明GSNSC在针对图查询的准确率上优于其他对比算法。

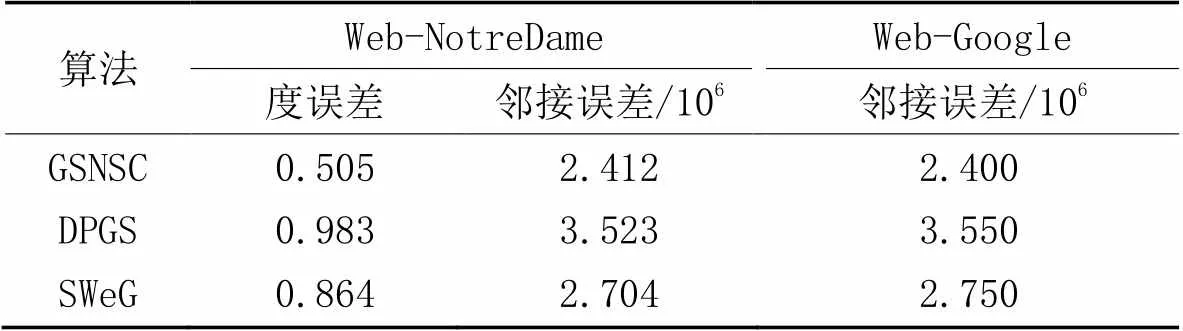
表4　不同数据集上3种算法的度误差和邻接误差对比

5 结语

本文结合图摘要和图压缩的优势，提出一种图摘要和图压缩的融合算法（GSNSC），用于压缩大规模图数据。经过理论分析和实验验证，结果表明所提算法具有较好的效果，所提融合算法具有一定的可行性。然而，本文算法目前只适用于简单静态同质图，还无法适用于异质图、属性图和动态图等。未来可以通过设置损失函数等方法，将本文算法扩充至属性图，根据不同节点的类型扩充至异质图，加入时间属性扩充至动态图。

[1] LEE K， JO H， KO J， et al. SSumM： sparse summarization of massive graphs［C］// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2020： 144-154.

[2] MACCIONI A， ABADI D J. Scalable pattern matching over compressed graphs via dedensification［C］// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 1755-1764.

[3] NAVLAKHA S， RASTOGI R， SHRIVASTAVA N. Graph summarization with bounded error［C］// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2008： 419-432.

[4] SEO H， PARK K， HAN Y， et al. An effective graph summarization and compression technique for a large-scaled graph［J］. The Journal of Supercomputing， 2020， 76（10）： 7906-7920.

[5] SHIN K， GHOTING A， KIM M， et al. SWeG： lossless and lossy summarization of web-scale graphs［C］// Proceedings of the 2019 World Wide Web Conference. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2019： 1679-1690.

[6] ZHOU H， LIU S， LEE K， et al. DPGS： degree-preserving graph summarization［C］// Proceedings of the 2021 SIAM International Conference on Data Mining. Philadelphia， PA： SIAM， 2021：280-288.

[7] ZHU L， GHASEMI-GOL M， SZEKELY P， et al. Unsupervised entity resolution on multi-type graphs［C］// Proceedings of the 2016 International Semantic Web Conference， LNCS 9981. Cham： Springer， 2016： 649-667.

[8] TIAN Y， HANKINS R A， PATEL J M. Efficient aggregation for graph summarization［C］// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2008： 567-580.

[9] YONG Q， HAJIABADI M， SRINIVASAN V， et al. Efficient graph summarization using weighted LSH at billion-scale［C］// Proceedings of the 2021 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2021： 2357-2365.

[10] UR R S， NAWAZ A， ALI T， et al. g-Sum： a graph summarization approach for a single large social network［J］. EAI Endorsed Transactions on Scalable Information Systems， 2021， 8（32）： No.e2.

[11] SACENTI J A P， FILETO R， WILLRICH R. Knowledge graph summarization impacts on movie recommendations［J］. Journal of Intelligent Information Systems， 2022， 58（1）： 43-66.

[12] BOLDI P， SANTINI M， VIGNA S. Permuting web graphs［C］// Proceedings of the 2009 International Workshop on Algorithms and Models for the Web-Graph， LNCS 5427. Berlin： Springer， 2009： 116-126.

[13] HERNÁNDEZ C， NAVARRO G. Compressed representations for Web and social graphs［J］. Knowledge and Information Systems， 2014， 40（2）： 279-313.

[14] BRISABOA N R， LADRA S， NAVARRO G.2-trees for compact Web graph representation［C］// Proceedings of the 2009 International Symposium on String Processing and Information Retrieval， LNCS 5721. Berlin： Springer， 2009： 18-30.

[15] FRANCISCO A P， GAGIE T， KÖPPL D， et al. Graph compression for adjacency-matrix multiplication［J］. SN Computer Science， 2022， 3（3）： No.193.

[16] EMAMZADEH ESMAEILI NEJAD A， JAHROMI M Z， TAHERI M. Graph compression based on transitivity for neighborhood query［J］. Information Sciences， 2021， 576： 312-328.

[17] YANG S， YANG Z， CHEN X， et al. Distributed aggregation-based attributed graph summarization for summary-based approximate attributed graph queries［J］. Expert Systems with Applications， 2021， 176： No.114921.

[18] LEE K， KO J， SHIN K. SLUGGER： lossless hierarchical summarization of massive graphs［C］// Proceedings of the IEEE 38th International Conference on Data Engineering. Piscataway： IEEE， 2022： 472-484.

[19] KE X， KHAN A， BONCHI F. Multi-relation graph summarization［J］. ACM Transactions on Knowledge Discovery from Data， 2022， 16（5）： No.82.

[20] KANG S， LEE K， SHIN K. Personalized graph summarization： formulation， scalable algorithms， and applications［C］// Proceedings of the IEEE 38th International Conference on Data Engineering. Piscataway： IEEE， 2022： 2319-2332.

[21] 董荣胜，张新凯，刘华东，等. 大规模图数据的2-MDD表示方法与操作研究［J］. 计算机研究与发展， 2016， 53（12）：2783-2792.（DONG R S， ZHANG X K， LIU H D， et al. Representation and operations research of2-MDD in large-scale graph data［J］. Jouanal of Computer Research and Development， 2016， 52（12）：2783-2792.）

[22] RISSANEN J. Modeling by shortest data description［J］. Automatica， 1978， 14（5）： 465-471.

[23] BRODER A Z， CHARIKAR M， FRIEZE A M， et al. Min-wise independent permutations［J］. Journal of Computer and System Sciences， 2000， 60（3）： 630-659.

[24] LeFEVRE K ， TERZI E. GraSS： graph structure summarization［C］// Proceedings of the 2010 SIAM International Conference on Data Mining. Philadelphia， PA： SIAM， 2010： 454-465.

Graph summarization algorithm based on node similarity grouping and graph compression

HONG Yu1， CHEN Hongchang2， ZHANG Jianpeng2*， HUANG Ruiyang2

（1，，450002，；2，，450002，）

To solve the problem that the current graph summarization methods have high compression ratios and the graph compression algorithms cannot be directly used in downstream tasks， a fusion algorithm of graph summarization and graph compression was proposed， which called Graph Summarization algorithm based on Node Similarity grouping and graph Compression （GSNSC）. Firstly， the nodes were initialized as super nodes， and the super nodes were grouped according to the similarity. Secondly， the super nodes of each group were merged until the specified number of times or nodes were reached. Thirdly， super edges and corrected edges were added between the super nodes for reconstructing the original graph. Finally， for the graph compression part， the cost of compressing and summarizing the adjacent edges of each super node were judged， and the less expensive one in these two was selected to execute. Experiments of graph compression ratio and graph query were conducted on six datasets such as Web-NotreDame， Web-Google and Web-Berkstan. Experimental results on six datasets show that， the proposed algorithm has the compression ratio reduced by at least 23 percentage points compared with SLUGGER （Scalable Lossless sUmmarization of Graphs with HiERarchy） algorithm， and the compression ratio decreased by at least 13 percentage points compared with SWeG （Summarization of Web-scale Graphs） algorithm. Experimental results on Web-NotreDame dataset show that the degree error of the proposed algorithm is reduced by 41.6% compared with that of SWeG algorithm. The above verifies that the proposed algorithm has better graph compression ratio and graph query accuracy.

graph summarization; graph compression; graph query; super edge; Minimum Description Length (MDL)

1001-9081（2023）10-3047-07

10.11772/j.issn.1001-9081.2022101535

2022⁃10⁃17；

2023⁃01⁃31；

国家自然科学基金资助项目（62002384）；中国博士后科学基金资助项目（2020M683760）。

宏宇（1998—），男，河北廊坊人，硕士研究生，主要研究方向：图数据挖掘； 陈鸿昶（1964—），男，河南新密人，教授，博士生导师，博士，主要研究方向：大数据分析、通信与信息系统； 张建朋（1988—），男，河北廊坊人，助理研究员，博士，主要研究方向：大数据分析； 黄瑞阳（1986—），男，福建漳州人，副研究员，博士，主要研究方向：知识图谱、文本挖掘。

TP391

A

2023⁃01⁃31。

This work is partially supported by National Natural Science Foundation of China （62002384）， China Postdoctoral Science Foundation （2020M683760）.

HONG Yu， born in 1998， M. S. candidate. His research interests include graph data mining.

CHEN Hongchang， born in 1964， Ph. D.， professor. His research interests include big data analysis， communication and information systems.

ZHANG Jianpeng， born in 1988， Ph. D.， research assistant. His research interests include big data analysis.

HUANG Ruiyang， born in 1986， Ph. D.， associate research fellow. His research interests include knowledge graph， text mining.