优化编码树单元级比特分配算法

杨栩，郭红伟，李婉雪

优化编码树单元级比特分配算法

杨栩1，2*，郭红伟3，4，李婉雪1

（1.成都师范学院 物理与工程技术学院，成都 611130； 2.重庆邮电大学 通信与信息工程学院，重庆 400065； 3.红河学院 工学院，云南 蒙自 661199； 4.电子科技大学 信息与通信工程学院，成都 611731）（ ∗ 通信作者电子邮箱yangxu@cdnu.edu.cn）

新一代视频编码标准H.266/VVC（Versatile Video Coding）的码率控制算法采用编码参数相互独立的率失真优化技术。然而，同一帧内的编码树单元（CTU）间在空域上相互影响，且存在全局编码参数；同时，CTU级比特分配公式采用近似的编码参数分配比特，进而降低了码率控制精度和编码性能。针对上述问题，提出空域全局优化CTU级比特分配算法RTE_RC（Rate Control with Recursive Taylor Expansion），并通过递归算法逼近全局编码参数。首先，建立空域全局优化比特分配模型；其次，应用递归算法求解CTU级比特分配模型中的全局拉格朗日乘子；最后，优化编码单元的比特分配并对编码单位进行编码。实验结果表明，在低延时P（Prediction）帧（LDP）配置下，与码率控制算法VTM_RC相比，所提算法的码率控制误差由0.46%下降至0.02%，码率节省了2.48个百分点，编码时间下降了3.52%，显著提升了码率控制精度和率失真性能。

比特分配；全局拉格朗日乘子；码率控制；递归泰勒展开；VVC

0 引言

通信技术的发展使视频数据在互联网中大规模传输变为可能，移动互联网技术的普及使视频数据传输的需求量也越来越大，有限的带宽难以满足海量增长的视频数据传输需求，视频数据压缩变得越发重要，视频编解码也成了学术界和工业界研究的重点。在最新一代视频编码标准H.266/VVC（Versatile Video Coding）下，压缩率进一步提升，相同主观质量下节省了50%左右的码率，但也极大地增加了编码复杂度。

码率控制（Rate Control， RC）［1］是视频编码最主要的研究内容之一，广泛应用于视频数据的编码和传输，特别是线上会议系统、直播平台等对实时性要求比较高的应用。在带宽限制条件下，实时传输质量稳定的视频数据并平衡压缩率、复杂度和准确率是码率控制中的复杂优化问题。

码率控制算法不仅影响视频的压缩效果，也影响视频的传输时延。码率控制分为比特分配和码率控制两个阶段，码率控制算法的目标可以总结为两方面：1）使目标码率在不同层次的编码单元上根据图像复杂度合理分配，图像复杂度由已编码帧的率失真性能反映；2）分配的目标码率尽可能完全使用，使实际编码码率和目标码率的误差趋近于零。

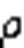
-模型中，拉格朗日乘子不仅可以用于比特分配阶段，在码率控制阶段，也可以使用它计算QP后直接用于编码；因此拉格朗日乘子会影响码率控制精度和编码率失真性能［6］，对码率控制效果产生决定性的影响。为了降低编码复杂度，编码器忽略编码单元间在时域、空域上的相关性，独立计算各个编码单元的失真、编码比特和率失真代价。编码器利用拉格朗日乘子进行预测模式的对比选择，然而编码单元间的编码参数在时域、空域、频域上存在密切的联系，特别是帧间预测采用的运动补偿预测（Motion Compensated Prediction， MCP）和运动矢量预测（Motion Vector Prediction， MVP）使编码单元在时域上存在相互依赖，所以许多研究［7-9］围绕考虑相关性的率失真优化展开，还有部分研究围绕优化比特分配展开。文献［4］中在帧级比特分配中考虑编码帧的时域相关性，通过改变全局拉格朗日乘子的权重系数为不同层级编码帧分配比特，在编码树单元（Coding Tree Unit， CTU）级比特分配中，根据图像复杂度为CTU分配比特。文献［10］中提出了用递归泰勒展开（Recursive Taylor Expansion，RTE）法计算全局拉格朗日乘子，并应用到HEVC（High Efficiency Video Coding）码率控制算法。文献［11-12］中将全局拉格朗日乘子应用到HEVC码率控制算法的比特分配阶段和码率控制阶段。文献［13］中提出了一种多目标码率控制，即在码率控制算法中减小编码失真，保证码率控制精度和减小质量波动等多个目标的联合优化。文献［14］中在参考帧和已编码帧之间建立依赖因子，并用于自适应比特分配算法，编码复杂度也有所增加。文献［15］中以结构相似性（Structural SIMilarity， SSIM）为评价指标优化比特分配。文献［16］中通过编码单元中选择SKIP模式的像素占比建立相应的码率控制模型，并应用到VVC参考代码中。然而在CTU级比特分配算法中，为了降低计算复杂度，VVC直接用同层级上一帧的帧级拉格朗日乘子分配编码帧的目标比特，由于当前编码帧和同层级上一帧的目标比特有较大的差距，使用相同的拉格朗日乘子进行比特分配不准确，码率控制精度和率失真性能仍然有进一步提升的空间。

比特分配公式为复杂的非线性函数，难以直接获取它的解析解。文献［17］中通过迭代算法逼近封闭解，从而优化码率控制；但是该算法重在优化计算机实现，没有从编码上建立完备的理论模型。受此启发，虽然同一帧内的CTU之间不存在时域相关性，但是当前编码CTU的编码性能受到它邻近已编码CTU的影响，在空域上存在相关性。为了能在空域上全局优化比特分配，有必要建立它的数学模型，确定全局编码参数，再通过迭代算法逼近它的全局解，并应用到新一代视频编码标准VVC。

目前VVC码率控制算法采用-模型，在CTU级码率控制中，由于当前帧还未编码，编码参数未知。为了简化问题，在分配帧级目标比特时，使用图像组（Group of Pictures， GOP）中同一层级的最近已编码帧的参数分配比特，由于使用已编码帧参数计算的比特和当前编码帧的目标比特不一致，将导致码率控制误差的累积。本文提出空域全局优化编码树单元级比特分配算法RTE_RC（Rate Control with Recursive Taylor Expansion），将码率分配公式中的全局拉格朗日乘子作为未知数，用目标比特和分配公式建立一个关于未知参数拉格朗日乘子的方程，使用RTE法［17］求解全局拉格朗日乘子，并应用于VTM（VVC Test Model）12.0中以优化CTU级比特分配，通过极少步的递归逼近全局解，降低编码复杂度，提升性能。

1 VVC码率控制算法

VVC码率控制算法分为比特分配和码率控制两个阶段。比特分配阶段将目标比特分配到不同的编码单元，即算法依据输入视频的内容、传输信道中带宽的上限和缓冲器的状态为编码单元分配恰当的比特数；在码率控制阶段，编码单元确定相应的量化参数QP以编码，即通过选择不同的量化参数使编码后的比特数和分配的比特数尽可能接近。

1.1　R-λ模型

为了降低编码复杂度，VVC码率控制技术同样采用独立率失真优化技术，码率控制问题变为在目标码率限定条件下最小化编码失真的问题，表达式为：

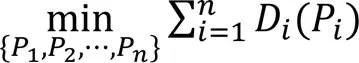
其中：为编码单元数；P为第个编码单元的参数（如量化参数、运动向量、划分方式等）；D和R分别为第个编码单元的编码失真和比特消耗；T为目标码率。

VVC标准参考代码VTM，采用信源服从柯西分布［18］的率失真模型：

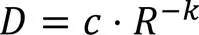
其中：和为模型参数；和分别为编码失真和编码比特，分别用均方误差（Mean Square Error， MSE）和单位像素所占比特（bit per pixel， bpp）表示。MSE通过原始帧和重建帧对应像素的均方误差求得，而bpp则通过目标码率与对应的像素总数的比值计算，码率控制算法在视频序列、GOP、帧、CTU不同层级进行比特分配，对应地，在不同层级上都有相应的bpp值。

通过拉格朗日乘子法将式（1）所示的有约束优化问题转化为无约束优化问题，即

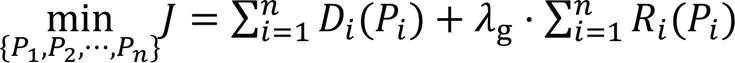
其中：为所有编码单元的率失真代价之和；g为全局拉格朗日乘子，即整个视频序列共享该拉格朗日乘子。式（3）中各离散变量间高度耦合，难以求解视频编码的优化问题。为简化问题，假设各编码单元互不相关，即每个编码单元的编码失真和编码比特数只与当前编码单元的编码参数有关，独立求解每个编码单元最优编码参数问题如下：

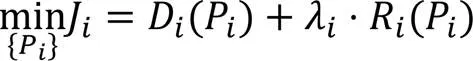
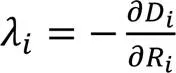
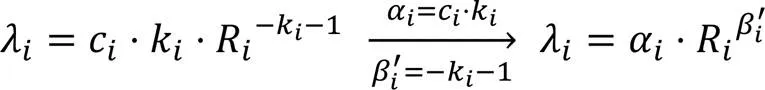
式（6）中的参数在编码完一帧或者一个CTU后，自动更新。根据式（2）和式（6）可以得到参数更新公式：

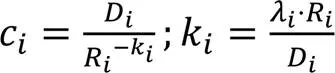
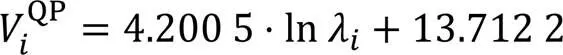
可以看出，码率控制算法中的量化参数和拉格朗日乘子的对数可以用线性函数关系拟合。

1.2　编码树单元级比特分配

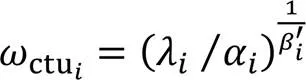
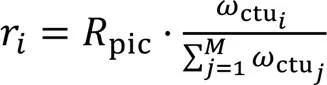
2 优化CTU级比特分配

为简化编码问题、降低复杂度，将各编码单元看作相互独立的个体，通过拉格朗日乘子法将约束性优化问题转换为非无约束性优化问题。为了能全局优化CTU级比特分配，需要找到最优参数并求解，再用于优化比特分配。

2.1　空域上全局优化比特分配问题

对于不考虑帧间CTU时域相关性的优化比特分配问题，即在编码帧目标比特限定条件下最小化编码失真，需要优化的参数为比特，编码第个CTU时，式（4）对r求偏导为0，建立等式：

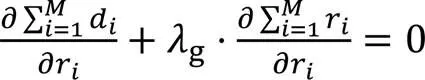
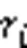
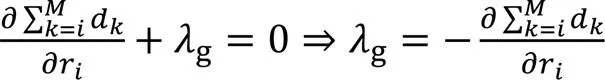
帧内所有CTU采用基于全局拉格朗日乘子g的-模型，可以优化比特分配，使编码失真最小。CTU都用相同的拉格朗日乘子意味着一帧内每一个比特的作用都相同，即增减一个比特所带来失真变化相同。CTU级比特分配问题为：在给定帧目标比特条件下，通过已编码帧对应CTU相关参数分配比特。计算公式如下：

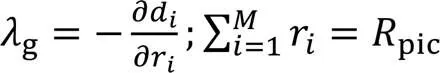
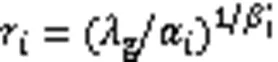
2.2　比特分配公式的泰勒展开式

根据上文的-模型，可得帧级分配的比特与各编码单元分配的比特关系为：

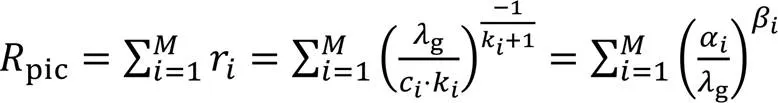
截断式（17）的4阶及其以上项，可得：

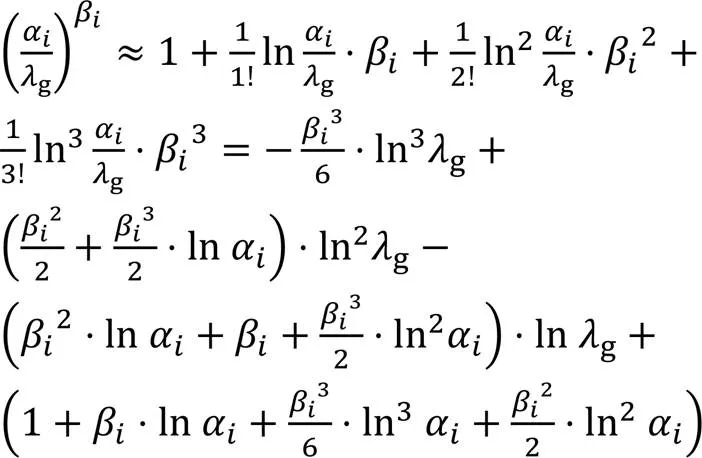
将式（18）代入式（16）可得：

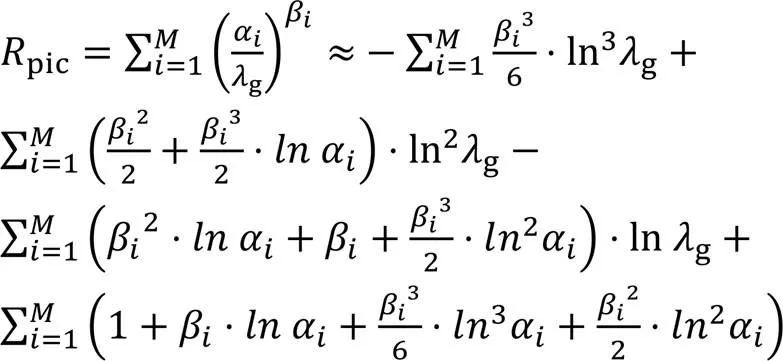
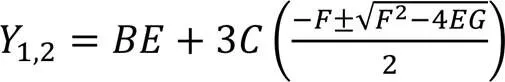
2.3　RTE求解编码用并优化比特分配

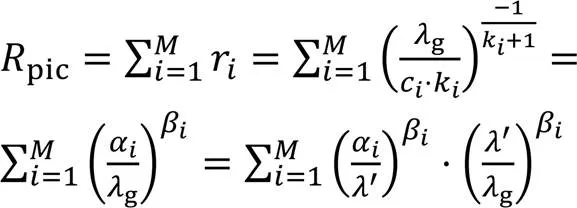
实际编码中递归结束条件为式（24）～（25）：

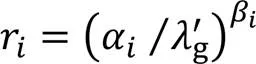
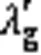
2.4　算法流程

算法 RTE_RC算法。

目标 计算全局拉格朗日乘子，并用于优化编码树单元级比特分配；

初始化 将参数初始化为同级上一帧相关参数。

for 每一个编码帧

通过初始拉格朗日乘子计算式（19）中、、、、、、

if 式（24）满足递归结束条件

若满足，结束递归

else

执行下一次循环

for 每一个CTU

码率控制阶段进行编码并更新CTU参数

if 最后一个CTU

更新帧参数

else

编码下一个CTU

完成视频序列编码

3 实验与结果分析

3.1　实验设置

为验证本文算法（RTE_RC）的有效性，将算法集成到VVC参考软件VTM12.0的码率控制算法中。以VTM12.0不开启码率控制作为基准，分别使用QP值22、27、32、37编码每个测试序列，所得的4个码率值作为码率控制实验的目标码率。

实验条件遵守国际编码标准组织JCT-VC（The Joint Collaborative Team on Video Coding）建议的通用测试条件 （Common Test Conditions， CTC），选用JCTVC-L1100［21］建议的具有不同分辨率类型的视频作为测试视频，包括ClassB、ClassC、ClassD和ClassE中的全部16个视频序列。编码器配置为低延时P帧（Low-Delay Prediction frame， LDP）。实验环境为Inter Core i7-7700K，CPU@4.2 GHz，内存16 GB，X64处理器，Windows10操作系统。

码率控制算法是在目标码率的限定下，尽可能降低失真，编码时间是衡量算法复杂度的重要参数，所以码率控制算法优劣的评价指标包括码率控制精度、编码时间和码率节省BD-rate（Bjøntegaard-Delta rate）。

码率控制精度为计算实际编码码率和目标码率的误差率，计算公式为：

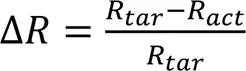
BD-rate是评价视频编码算法率失真性能的主要参数之一，表示新算法相较于原算法的码率节省。BD-rate为负值时，表示在相同峰值信噪比（Peak Signal-to-Noise Ratio， PSNR）下码率节省，反之码率增加。格式为YUV420的原始视频包含亮度Y、色度U、色度V这3个通道，人眼对亮度更加敏感，一般主要比较亮度分量的BD-rate（Y）。

编码时间是衡量算法编码复杂度的重要指标，通过比较绝对编码时间或者相对编码时间评价编码复杂度。

3.2　对比算法

为了说明RTE_RC的有效性，将RTE_RC与主流算法进行对比。基准算法为H.266/VVC的参考代码自带的码率控制算法（Rate Control algorithm Versatile Test Model ， VTM_RC），基准算法集成了最新的编码算法，在此基础上还能提升编码性能，具有较好的对比意义。码率控制中的目标码率是通过固定QP算法（FIXED_QP）编码每一个视频序列获得。文献［22-23］算法是码率控制中非常经典的算法，文献［22］算法实现低复杂度下质量稳定的码率控制，文献［23］算法在-模型下实现自适应比特分配。为了进一步提升率失真性能，文献［16］算法考虑了残差系数为0的SKIP模式对编码率失真参数的影响，并建立质量依赖因子用于编码，取得了较好的率失真性能。本文实验主要从编码时间、码率控制精度和码率节省三方面进行对比分析。

3.3　码率控制精度对比

3.4　率失真性能对比

本文实验还对比了不同算法的BD-rate，如表1所示。RTE_RC总体平均BD-rate为0.55%，远低于VTM-RC算法的3.03%，码率节省了2.48个百分点。与文献［16］算法相比，RTE_RC的率失真性能较低，这是因为RTE_RC以VTM为基准，而文献［16］算法以HM为基准。RTE_RC在率失真性能上也优于文献［22-23］算法。

表1　不同比特分配优化算法性能对比 单位：%

为了直观地观察率失真性能提升情况，图1给出了不同测试序列中，在LDP下RTE_RC与VTM_RC的率失真曲线。从图1可以看出，PSNR越高，率失真性能越好， RTE_RC率失真性能优于VTM_RC。

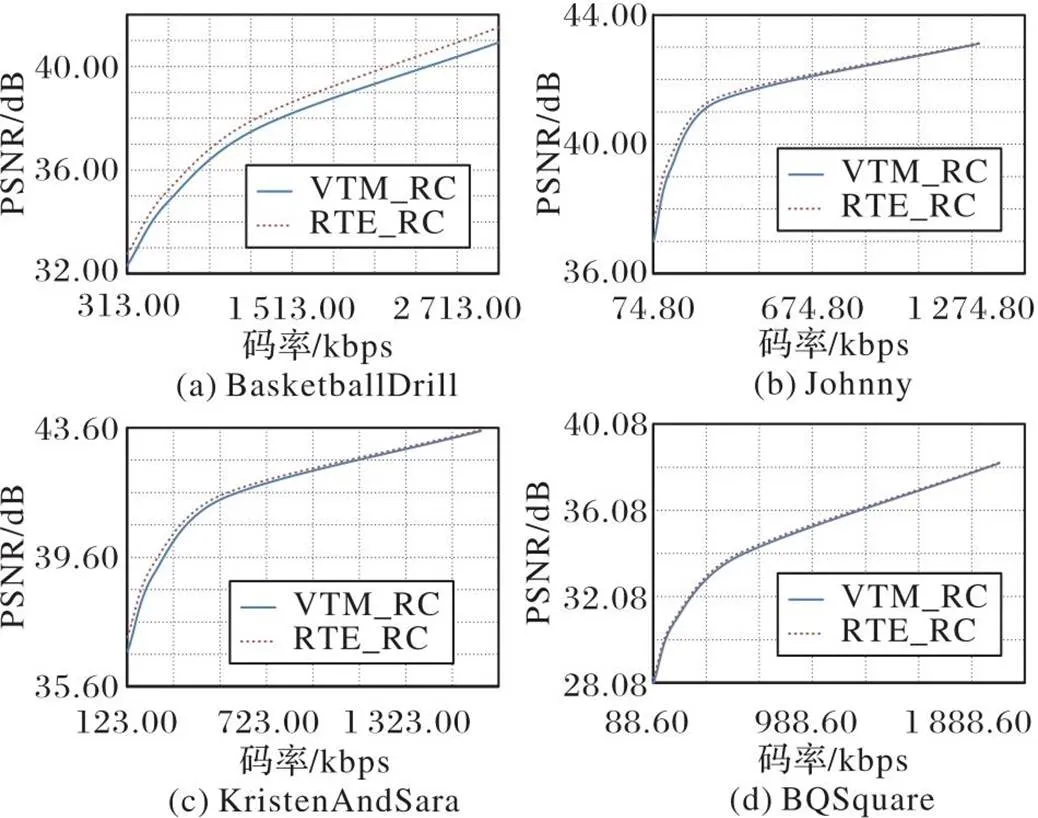
图1　不同算法在不同测试序列中的率失真性能比较

表2对比了不同算法下亮度分量（Y）和色度分量（U、V）的BD-rate。RTE_RC色度分量的平均BD-rate分别为-2.10%和-1.98%，VTM_RC色度分量的平均BD-rate分别为3.40%和3.63%，RTE_RC在色度分量上的码率节省更多。

表2　各分量在VTM_RC和RTE_RC下BD-rate对比 单位：%

由于VTM通过滑动窗将误差往后累积并平均分配到未编码帧，越往后，突击消化误差的情况越多，不仅影响编码率失真性能，还会增加控制误差。本文算法针对图像变化缓慢的视频序列效果更明显，对于人像视频或者背景固定的视频，图像率失真特性较稳定，如果分配得更准，则更符合编码单元的率失真特性。表1中ClassE类的BD-rate节省最多也说明了这个问题。

3.5　编码时间对比

RTE_RC、VTM_RC与用于计算目标码率的固定QP编码算法（FIXED_QP）编码所有测试序列所用绝对时间如表3所示。

从表3可以看出，RTE_RC的编码时间低于VTM_RC和FIXED_QP，并且RTE_RC相较于VTM_RC的编码时间减少了3.52%。虽然采用递归算法，但是编码复杂度没有提高，主要原因是：1）次数较少，每次递归不超过3次就能达到10-10的控制误差，递归算法相较于运动搜索和其他编码环节所花时间较少；2）更精准的码率控制，或者更符合编码单元率失真特性的比特分配，使图像更稳定，不存在图像质量波动较大的情况，从长远看，能在编码模式选择和图像划分中节省时间；3）因为率失真性能的提升，编码模式选择时间更少，如背景固定的视频，有更大可能选择SKIP编码模式，从而缩短时间。

表3　不同算法的编码时间对比 时间：h

4 结语

线上视频会议、线上教学正逐步得到推广，而高稳定低延时系统是保证良好用户体验的前提，这也对码率控制算法提出了更高的要求，进一步提高码率控制精度和率失真性能，同时降低编码时间是码率控制面临的主要问题。本文分析了VVC码率控制系统的-模型，通过递归泰勒展开法计算每帧中所有CTU的全局拉格朗日乘子并应用于更新CTU权重系数，以此优化比特分配。实验结果表明，RTE_RC能较大程度提高码率控制精度和率失真性能，而且缩短了编码时间。但是本文主要解决了比特优化分配的问题，如何能让分配的比特使用得更合理是下一步研究的重点。

[1] 郭红伟，朱策，周益民. HEVC 码率控制技术的研究进展［J］. 重庆邮电大学学报（自然科学版）， 2018， 30（2）： 199-209.（GUO H W， ZHU C， ZHOU Y M. Recent advances on rate control for HEVC［J］. Journal of Chongqing University of Posts and Telecommunications （Natural Science Edition）， 2018， 30（2）：199-209.）

[2] LIU Y， LI Z G， SOH Y C. A novel rate control scheme for low delay video communication of H.264/AVC standard［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2007， 17（1）： 68-78.

[3] HE Z， KIM Y K， MITRA S K. Low-delay rate control for DCT video coding via /spl rho/-domain source modeling［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2001， 11（8）： 928-940.

[4] LI L， LI B， LI H， et al.-domain optimal bit allocation algorithm for high efficiency video coding［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2018， 28（1）： 130-142.

[5] LI B， LI H， LI L， et al. λ domain rate control algorithm for high efficiency video coding［J］. IEEE Transactions on Image Processing， 2014， 23（9）： 3841-3854.

[6] 郭红伟，朱策，刘宇洋. 视频编码率失真优化技术研究综述［J］. 电子学报， 2020， 48（5）： 1018-1029.（GUO H W， ZHU C， LIU Y Y. Overview of rate-distortion optimization for video coding［J］. Acta Electronica Sinica， 2020， 48（5）：1018-1029.）

[7] GAO Y， ZHU C， LI S， et al. Temporally dependent rate-distortion optimization for low-delay hierarchical video coding［J］. IEEE Transactions on Image Processing， 2017， 26（9）： 4457-4470.

[8] GAO Y， ZHU C， LI S， et al. Source distortion temporal propagation analysis for random-access hierarchical video coding optimization［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2019， 29（2）： 546-559.

[9] YANG T， ZHU C， FAN X， et al. Source distortion temporal propagation model for motion compensated video coding optimization［C］// Proceedings of the 2012 IEEE International Conference on Multimedia and Expo. Piscataway： IEEE， 2012： 85-90.

[10] LI S， XU M， WANG Z， et al. Optimal bit allocation for CTU level rate control in HEVC［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2017， 27（11）： 2409-2424.

[11] GUO H， ZHU C， XU M， et al. Inter-block dependency-based CTU level rate control for HEVC［J］. IEEE Transactions on Broadcasting， 2020， 66（1）： 113-126.

[12] GUO H， ZHU C， GAO Y， et al. A frame-level rate control scheme for low delay video coding in HEVC［C］// Proceedings of the IEEE 19th International Workshop on Multimedia Signal Processing. Piscataway： IEEE， 2017： 1-6.

[13] LIU F， CHEN Z. Multi-objective optimization of quality in VVC rate control for low-delay video coding［J］. IEEE Transactions on Image Processing， 2021， 30： 4706-4718.

[14] MAO Y， WANG M， WANG S， et al. High efficiency rate control for versatile video coding based on composite Cauchy distribution［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2022， 32（4）： 2371-2384.

[15] LI Y， MOU X. Joint optimization for SSIM-based CTU-level bit allocation and rate distortion optimization［J］. IEEE Transactions on Broadcasting， 2021， 67（2）： 500-511.

[16] LI Y， LIU Z， CHEN Z， et al. Rate control for versatile video coding［C］// Proceedings of the 2020 IEEE International Conference on Image Processing. Piscataway： IEEE， 2020： 1176-1180.

[17] 北京航空航天大学. 一种基于最佳比特分配的HEVC CTU级码率控制方法：201510882801.X［P］. 2016-03-23.（Beihang University. A HEVC CTU level bit rate control method based on optimal bit allocation： 201510882801.X［P］. 2016-03-23.）

[18] KAMACI N， ALTUNBASAK Y， MERSEREAU R M. Frame bit allocation for the H.264/AVC video coder via Cauchy-density-based rate and distortion models［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2005， 15（8）： 994-1006.

[19] LI B， XU J， ZHANG D， et al. QP refinement according to Lagrange multiplier for high efficiency video coding［C］// Proceedings of the 2013 IEEE International Symposium on Circuits and Systems. Piscataway： IEEE， 2013： 477-480.

[20] LI B， XU J， LI H. Refining QP to improve coding efficiency in AVS［C］// Proceedings of the 2013 IEEE International Conference on Image Processing. Piscataway： IEEE， 2013： 1528-1531.

[21] BOSSEN F. Common test conditions and software reference configurations［EB/OL］. ［2022-04-11］.https：//www.itu.int/wftp3/av-arch/jctvc-site/2010_07_B_Geneva/JCTVC-B300.doc.

[22] WANG M， NGAN K N， LI H. Low-delay rate control for consistent quality using distortion-based Lagrange multiplier［J］. IEEE Transactions on Image Processing， 2016， 25（7）： 2943-2955.

[23] LI B， LI H， LI L. Adaptive bit allocation for R-lambda model rate control in HM［C］// Proceedings of the 13th Meeting of Joint Collaborative Team on Video Coding of ITU-T SG1 6WP3 and ISO/IEC JTC1/SC. ［S.l.］： JCTVC， 2013： 29.

Optimized bit allocation algorithm for coding tree unit level

YANG Xu1，2*， GUO Hongwei3，4， LI Wanxue1

（1，，611130，；2，，400065，；3，，661199，；4，，611731，）

It the rate control algorithms of the new generation video coding standard H.266/VVC （Versatile Video Coding）， the rate-distortion optimization technique with independent coding parameters is adopted. However， the Coding Tree Units （CTUs） within the same frame affect others in the spatial domain， and there are global coding parameters. At the same time， in the CTU-level bit allocation formulas， approximated coding parameters for bit allocation are used， resulting in the reduction of rate control accuracy and coding performance. To address these issues， a spatial-domain global optimization algorithm for CTU-level bit allocation called RTE_RC （Rate Control with Recursive Taylor Expansion） was proposed， and the global coding parameters were approximated by using a recursive algorithm. Firstly， a globally optimized bit allocation model in spatial-domain was established. Secondly， a recursive algorithm was used to calculate the global Lagrange multiplier in the CTU-level bit allocation formula. Finally， the bit allocation of coding units was optimized and the coding units were coded. Experimental results show that under the Low-Delay Prediction frame （LDP） configuration， compared with the rate control algorithm VTM_RC （Rate Control algorithm Versatile Test Model）， the proposed algorithm has the rate control error decreased from 0.46% to 0.02%， the bit-rate saved by 2.48 percentage points， and the coding time reduced by 3.52%. Therefore， the rate control accuracy and rate distortion performance are significantly improved by the proposed algorithm.

bit allocation; global Lagrange multiplier; rate control; Recursive Taylor Expansion (RTE); Versatile Video Coding (VVC)

This work is partially supported by National Natural Science Foundation of China （62061015）， Special Scientific Research Project of Chengdu Normal University （ZZBS2020-11）.

YANG Xu， born in 1983， Ph. D. candidate， lecturer. His research interests include panoramic video coding and communication， machine learning based video coding.

GUO Hongwei， born in 1980， Ph. D.， professor. His research interests include video coding and communication， image processing.

LI Wanxue， born in 1992， Ph. D.， lecturer. Her research interests include image processing， video coding.

1001-9081（2023）10-3195-07

10.11772/j.issn.1001-9081.2022091410

2022⁃09⁃22；

2022⁃11⁃28；

国家自然科学基金资助项目（62061015）；成都师范学院专项科研项目（ZZBS2020⁃11）。

杨栩（1983—），男，四川苍溪人，讲师，博士研究生，CCF会员，主要研究方向：全景视频编码及通信、基于机器学习的视频编码； 郭红伟（1980—），男，云南金平人，教授，博士，CCF高级会员，主要研究方向：视频编码及通信、图像处理； 李婉雪（1992—），女，四川成都人，讲师，博士，主要研究方向：图像处理、视频编码。

TN919.81

A

2022⁃12⁃07。