白鹤滩泄洪洞横向三支臂弧门设计关键技术

2023-10-21胡坚柯金晓华吕飞鸣朱烨森

中国农村水利水电 2023年10期

胡坚柯，金晓华，吕飞鸣，朱烨森

（中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122）

1 概述

白鹤滩泄洪洞规模较大，泄洪洞弧门孔口尺寸（15 m× 9.5 m）和设计水头（58 m）等参数均属国内外最大水平之列［1］，而泄洪洞在严苛的技术参数要求下面临巨大的破坏风险。泄洪洞闸门及启闭机布置见图1，在进水口布置有一道事故闸门和一道潜孔弧形工作闸门。为降低泄洪洞空蚀风险，采取降低单宽流量、减小水深等措施以降低出口消能防冲难度、提高洞身运行安全。白鹤滩泄洪洞宽高比达1.58，常规二支臂弧门难以满足变形控制及水封要求，且大宽度弧门抗流激振动能力不足。据调查，在中国、德国、日本等国内外闸门设计规范和设计手册中均未提到横向多支臂结构形式的弧门［2］，在国内，横向三支臂弧门在国内工程中尚无应用实例，因而白鹤滩泄洪洞弧门亟需寻求横向三支臂弧门技术体系［3］。

图1 泄洪洞闸门及启闭机布置图Fig.1 Layout of spillway tunnel gate and hoist

白鹤滩泄洪洞弧形闸门主梁结构形式可采用主横梁结构和主纵梁结构［4-6］，考虑门叶分节、运输、制造及安装要求，主横梁结构的弧门形式更优［7-9］。泄洪洞弧门选用容量为2×5 000 kN液压启闭机进行操作，可动水启闭以及局部开启运行。

白鹤滩泄洪洞横向三支臂弧门基本布置形式如图1（b）所示，为了保证弧门结构能够满足挡水及运行要求，对横向三支臂的支臂位置、单位刚度比选取进行了优化分析［10-13］，并进一步对横向三支臂弧门在全关设计水头工况（面板承受58 m 水头），以及设计洪水位下弧门开启瞬间工况（面板承受58 m 水头+吊点启闭力2×5 000 kN）下的结构受力及变形进行分析。

2 横向三支臂弧门支臂位置优化分析

2.1 支臂位置参数设置

白鹤滩泄洪洞横向三支臂弧门的载荷受力如图2（a）所示，其中主要受到挡水时的水压力，以及液压启闭机操作闸门时的启闭力。白鹤滩泄洪洞弧门设计水头58.00 m，考虑动载系数和地震荷载系数后，设计总水压力约为118 700 kN。横向三支臂弧形闸门面板外缘曲率半径为19 m，支铰形式为球铰，采用自润滑球面滑动轴承支承。

图2 泄洪洞弧门受力示意图Fig.2 Schematic diagram of the force on the spillway tunnel arc door

如图2（b）所示为横向三支臂弧门的内力分布示意图，内力分布满足多跨连续梁的超静定结构特点，其中，主横梁悬臂长度为a（m），Mx、Ma、Mb、Mc、Ml为主框架横梁弯矩，Mh为支臂弯矩，H为侧向力，Na、Nb、Nc为支承反力，Ra、Rc为支座反力。对于非常规的横向三支臂弧门主框架悬臂长度取值，应尽量确保三个支臂反力的差值较小，且主框架结构的内力以及变形分布均匀，进而利于闸门以及依附的土建结构的整体稳定。将横向三支臂弧门主框架的内力分配按中间支臂设置在孔口中心线上，分别选取主横梁悬臂段长度为2、2.1、2.2、2.3、2.4、2.5、2.6、3 m进行弧门内力计算分析。

2.2 计算结果

如图3所示为不同悬臂长度时横向三支臂弧门主框架的内力和弯矩分布情况。当悬臂段长度a在2.2～2.5 m 范围内时，Mx与Ma（Mc）、Ml、Mb的差值相对较小，主框架横梁的弯矩分布比较均匀，其中以悬臂段长度为2.3 m 时弯矩分布最为均匀；当主框架横梁悬臂段长度a在2.4～2.5 m 范围内时，主框架支承反力差值最小，主框架横梁部分的弯矩分布相对均匀；当悬臂段长度a在2.2～2.5 m 范围内时，主框架所受的侧向力和支臂弯矩都较小，其中悬臂段长度a在2.3～2.4 m 范围内时，侧向力最小；当a为2.5 m时，主框架横梁部分的弯矩分布相对均匀，最大差值为9 796 kN·m，主框架支承反力差值最小为810 kN。考虑白鹤滩泄洪洞扁宽型结构特点［11，12］，横向三支臂弧门的主横梁悬臂长度值为2.5 m是较优的设计方案。

图3 三支臂弧门悬臂长度对内力和弯矩分布影响Fig.3 Influence of cantilever length on the distribution of internal force and bending moment

3 横向三支臂弧门单位刚度比优化分析

3.1 单位刚度比参数设置

三支臂弧门的主横梁与支臂的单位刚度比计算公式为：

式中：I1为主横梁的截面惯性矩；h为支臂计算长度；I2为支臂的截面惯性矩；L为主横梁计算跨度。

参照《水电工程钢闸门设计规范》（NB 35055-2015），直支臂弧形闸门主横梁与支臂的单位刚度比推荐选用4～11，而对于相同孔口宽度和设计水头的横向三支臂弧门，其主横梁计算跨度L值约为常规二支臂弧门的1/2，因此，为了保证三支臂弧门结构刚度满足设计要求［13］，进一步研究主横梁与支臂的单位刚度比横向三支臂弧门的结构的影响，分别选取单位刚度比K0为3、4、5、6、7、8、9、10、11进行主框架内应力计算分析。

3.2 计算结果

如图4所示为不同单位刚度比时横向三支臂弧门主框架内力和弯矩分布情况。基于弧门悬臂长度对结构内力分布影响研究，弧门结构的悬臂段长度为2.5 m，此时悬臂段最大弯矩Mx为定值。由图4（a）可知，随着单位刚度比K0的增加，主框架侧向力H越来越小，由此产生的支臂弯矩Mh也越来越小；而随着单位刚度比K0的增加，边支座与中间支座反力的差值增大，但是增加幅度较小，并且逐步趋于均匀，表明单位刚度比对支座反力的影响不大。由图4（b）可知，随着单位刚度比K0的增大，弯矩Ma、Mb以及Ml值几乎没有变化，表明单位刚度比对主横梁弯矩分配的影响很小。

参照《水电工程钢闸门设计规范》，设置合理的弧形闸门主横梁与支臂的单位刚度比的目的是为了使弧形闸门主横梁与支臂的结构相匹配、整体受力更均匀，即能尽量提高弧门整体结构的承载利用率［13］。针对横向三支臂弧门，主横梁的计算跨度L值约为常规弧门的一半，使得单位刚度比K0值约为相同尺寸的常规弧门的两倍。

因此，依据等载荷布置原则，选定两根主横梁布置方案，白鹤滩泄洪洞横向三支臂弧门主横梁与支臂结构尺寸如图5 所示，其中主横梁的截面惯性矩I1为19 662 741.4 mm4，支臂计算长度hz为17 914 mm，支臂的截面惯性矩I2为6 611 292.5 mm4，主横梁计算跨度L为500 mm。由式（1）计算得到的单位刚度比为10.7，对照上述分析结果，该主框架形式为较优的方案。

图5 主横梁和支臂结构尺寸（单位：mm）Fig.5 Structural dimensions of main beam and arm

4 横向三支臂弧门结构有限元分析

4.1 计算模型及工况

根据横向三支臂弧门支臂位置和单位刚度比的优化分析，选取三支臂弧门悬臂长度为2.5 m，并以此建立如图6（a）所示的弧门结构有限元三维模型。如图6（b）～（e）所示为弧门结构的网格划分情况，该模型共有结点169 829 个，单元299 152 个，其中壳单元134 218 个，用以模拟弧门面板、水平梁、纵梁、支臂等弧门中具有板壳特征的构件；实体单元161 570 个，用以模拟支铰结构。白鹤滩泄洪洞三支臂弧门的水平梁、纵梁以及支臂材料选用Q345C 钢材，支铰中的活动铰和固定铰选用ZG35CrMo 铸钢，铰轴选用35CrMo 钢。弧门主要构件的材料、厚度参数如表1所示。

表1 主要构件的材料特性Tab.1 Material characteristics of major components

图6 主横梁和支臂结构尺寸Fig.6 Structural dimensions of main beam and arm

由于弧门在全关状态时，总水压力最大、水柱力最大，即此时总载荷最大；同时，若此时进行启门操作，考虑动载荷后风险最大。因而通过对弧门两种工况进行计算模拟，工况1 用以模拟弧形闸门全关挡设计洪水位（挡水水头58 m）下的受力工况，工况2 用以模拟弧形闸门在设计洪水位下开启瞬间（启闭力2×5 000 kN）的受力工况。详细载荷及模型约束见表2。

表2 工作闸门运行工况Tab.2 Operating condition of service gate

4.2 计算结果

图7 和图8 展示了两种工况下弧门整体以及各构件的位移及应力等色图。其中，图7（a）和图7（b）分别为工况1 时闸门的总位移和Mises 应力，图7（c）～（i）分别代表面板、水平梁、纵梁、支臂、固定铰、活动铰、铰轴的Mises应力。同样地，图8（a）和图8（b）分别为工况2时闸门的总位移和Mises应力，图8（c）～（i）分别代表面板、水平梁、纵梁、支臂、固定铰、活动铰、铰轴的Mises应力。如表3所示为两个工况下由数值计算得到的弧门结构主要构件的最大Mises应力结果。

表3 基于有限元数值计算的各构件最大Mises应力结果（含应力集中）Tab.3 The results of maximum Mises stress of each component based on finite element calculation （Including stress concentration）

图7 工况1时弧门整体和各部位的位移及应力数值计算结果云图Fig.7 The displacement and Mises stress results of the gate and all parts under working condition 1

对照图7 和图8 所示的应力云图可知，在构件之间的个别连接处或构件截面突然变化的位置，存在应力徒增的现象，这与结构存在应力集中以及有限元网格出现畸变有关，在实际构件中，需要将数值计算出现的集中应力进行剔除。

为了验证数值计算的准确性，选取水平梁为例进行连续梁弯矩求解，得到如图9所示的计算简图。

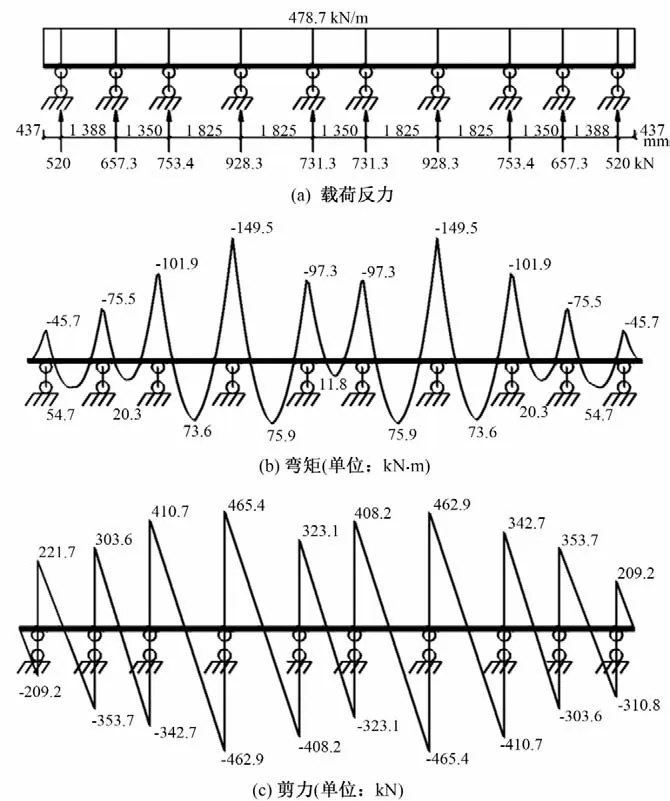
图9 水平梁计算简图Fig.9 Horizontal beam calculation diagram

基于《水电工程钢闸门设计规范》（NB 35055-2015）的计算要求，

式中：σ为弯曲应力；M为弯矩；W为截面模量；τ为剪切应力；Q为剪力；S为截面矩；I为惯性矩；δ为板厚；σ'为折算应力。得到水平梁最大应力约65 MPa，对应于表4 所示的81.8 MPa 结果在合理范围之内。通过相似的验证手段，优化后的工作闸门各构件最大Mises应力计算结果如表4所示。

表4 优化后的各构件Mises应力范围（剔除应力集中）Tab.4 The Mises stress range of each component after optimization（After removing stress concentration）

对比表4 中工况1 和工况2 的计算结果，工作弧门在工况2（设计洪水位下开启瞬间）下的整体应力水平大于在工况1（全关挡设计洪水位库水）下的整体应力水平，特别是弧门启吊点处的局部应力明显增大。在工况2（设计洪水位下开启瞬间）下，弧门结构的主要应力不超过145.00 MPa。

图10 展示了两种运行工况下弧门面板上三道横向水平线（顶水封部位、闸门最大合位移所在的中部水平线，底水封部位）上的位移分布情况。如图10 所示，工况1（全关挡设计洪水位库水）下面板顶水封部位的最大合位移为8.61 mm，横向最大位移差小于0.24 mm；面板中部最大合位移为14.75 mm，横向最大位移差小于2.11 mm；面板底水封部位最大合位移为13.25 mm，横向最大位移差小于0.42 mm。而在工况2（设计洪水位下开启瞬间）下面板顶水封部位的最大合位移为6.84 mm，横向最大位移差小于0.89 mm；面板中部最大合位移为11.10 mm，横向最大位移差小于2.59 mm；面板底水封部位最大合位移为6.54 mm，横向最大位移差小于1.57 mm。