超宽带高功率脉冲对裸导线的耦合特性分析

刘翔宇,韩玉兵,李炎新

(南京理工大学 电子工程与光电技术学院,南京 210094)

随着电磁技术的不断发展,战争形式已变为遍布海、陆、空、天、电的5维空间战争。而电磁技术的广泛应用,使5维空间作战依赖于各种信息化作战装备和系统,如雷达、通信、导航、敌我识别及遥测遥控等装备系统。若这些系统无法在复杂电磁环境中稳定工作,将导致战场感知迷茫、指挥协同紊乱及用频装备效能下降,影响甚至误导指挥决策,令交战双方作战能力的不对称优势逐渐扩大。而电力系统能量和信息的安全传输对装备及分系统至关重要。线缆作为信息和能量的基础传输媒介,确保系统中设备的正常运转及电能的高效率传送。传输线缆高稳定性、高可靠性的运行是保障装备及分系统正常运转的基础[1]。在整个信息与能量传输的过程中,需避免强电磁脉冲对传输线缆的影响。

超宽带高功率脉冲(ultra-wideband high power pulse,UWBHPP)作为一种强电磁脉冲,电磁能量可通过线缆、天线和孔缝等途径与装备分系统耦合,造成设备的降级、损坏甚至瘫痪,这对线缆的屏蔽性能提出了更高的要求。因此,开展UWBHPP裸露导线的耦合效应的研究,对保障装备及分系统的安全工作十分重要。安霆等[2]研究了UWBHPP、高空核爆电磁脉冲(high altitude electromagnetic pulse, HEMP)作用下长线缆的耦合效应;张鑫[3]提出了同轴线芯上电流计算模型,并建立了耦合方程,求解了屏蔽线芯耦合能量;陈旭[4]基于时频域等效性和最小相位原理求解了屏蔽线电流;丁昱[5]利用 时域有限积分法(finite integration technique,FIT) 法研究了 HEMP 作用下,同轴线终端的耦合特性,并分析了不同电场方向、不同线缆长度、不同孔缝大小及不同同轴线外导体厚度和不同电导率下耦合系数的变化规律;黄聪顺等[6]采用传输线的方法,数值模拟了HEMP作用下地面附近电缆屏蔽层的皮电流,并分析了皮电流随线缆长度、线缆屏蔽层两端接地状态及入射场方向的变化规律;Paul[7]最早将多导体传输线理论应用于电磁兼容,并建立了三导体传输线模型,模拟分析了线缆近远端串扰效应;Gassab等[8]基于多导体传输线理论,建立了多层绞缠双绞线束在平面波激励下的电磁耦合模型,给出了平均单位长度电参数的计算方法,预测了不同入射方向平面波激励下线缆束负载上的共模电流;D’Amore等[9]采用场线耦合的传输线模型,重点研究了外界电磁场与屏蔽多导体线的场线耦合效应,并运用电路模型研究了外界电磁场与屏蔽电缆之间的集总参数矩阵方程;Pignari等[10]提出一种用于预测无限大平面上,双绞线在平面波干扰下负载响应的传输线模型,给出了等效感应集总电压源的解析表达式和干扰强度的近似上限。目前,国内外对高功率脉冲的线缆耦合特性研究较少,主要还集中在HEMP对线缆耦合特性的研究。

本文基于时域有限差分法,分析了不同UWBHPP对裸露导线的强电磁脉冲耦合效应,分别从线缆长度、UWBHPP上升沿及脉冲宽度3方面,对线缆上耦合电压的影响进行了对比分析,为线缆的屏蔽效能及电磁防护设计提供了依据。

1 传输线的理论模型

暴露于高功率微波环境中的电缆,可在内部出现干扰电流或电压。在高功率微波作用下,电缆外导体上将感应出干扰电流和电压,再通过电缆本身的转移阻抗,激励电缆的内部,在芯线上感应出干扰电流或电压。高功率微波在电缆上的耦合过程,通常采用传输线方程来描述,适用的条件是电磁波的波长大于传输线的截面[11]。

常见的传输线模型分别为Agrawal模型[12]、Taylor模型[13]及Rashidi模型[14]。3种模型的搭建方法虽不一样,但经过分析后,3种电路模型得出的响应结果是一样的[15]。图1为Agrawal场线耦合等效模型。

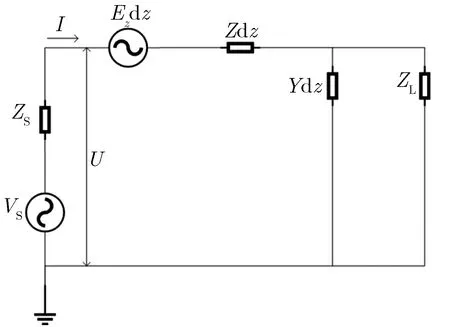
图1 Agrawal场线耦合等效模型Fig.1 Agrawal field line coupling equivalent model

由文献[7]可知,当频率为ω的平面波作用于图1所示的传输线上时,沿线的电压U和电流I满足的微分方程可表示为

(1)

(2)

其中:Ez为瞬态干扰电场强度;Z和Y分别为单位长度线缆的阻抗和导纳,可表示为

Z=R+jωL

Y=G+jωC

(3)

其中:R,L,G,C分别为单位长度线缆的电阻、电感、电导和电容;j为虚数单位;ω为照射角频率。

对式(1)和式(2)求导,并联立可得二阶微分方程,表示为

(4)

(5)

2 仿真实验

裸导线单线仿真模型如图2示。图2中导线为25_AWG、无屏蔽层裸导线,离地高度为10 cm,负载阻抗为50 Ω;采用有限大矩形理想导体来模拟大地。

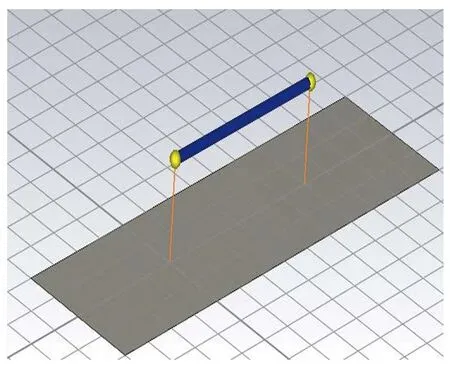
图2 裸导线单线仿真模型Fig.2 Simulation model for a single cable of exposed conductors

UWBHPP激励源为平面波,使用3种不同的UWBHPP信号辐照裸露导线,具体参数如表1所列。tr,wp,fc,wpb分别为UWBHPP信号的上升沿、脉冲宽度、中心频率及相对带宽;fh,fl分别为微波脉冲峰值功率谱密度下降3 dB时,所对应的频率上限和频率下限。平面波沿-z方向垂直辐照裸导线,电场强度E为6 000 V·m-1。

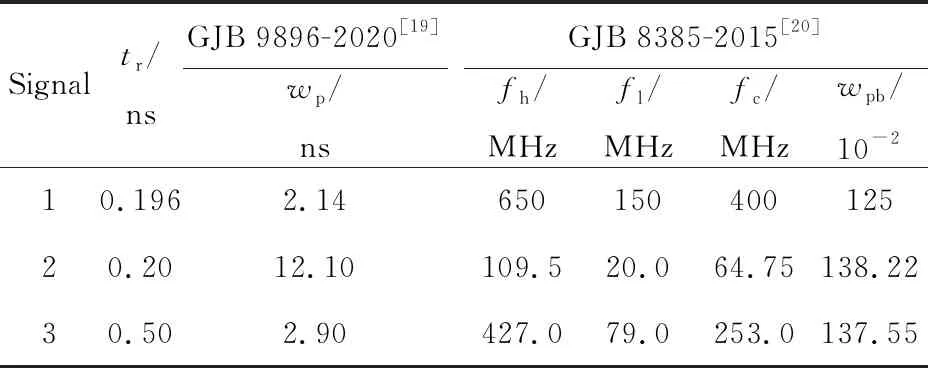
表1 3种UWBHPP信号参数Tab.1 Three types of UWBHPP signal parameters

图3和图4分别为3种激励源信号的时域波形和归一化频谱图。由图3可见:当激励源为信号2时,上升沿与信号1接近,但脉冲宽度约为信号1的6倍;当激励源为信号3时,上升沿与信号1及信号2均不同,脉冲宽度比信号1略大。

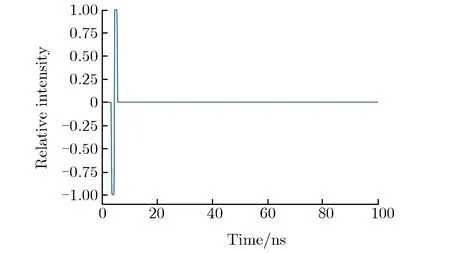
(a) Signal 1

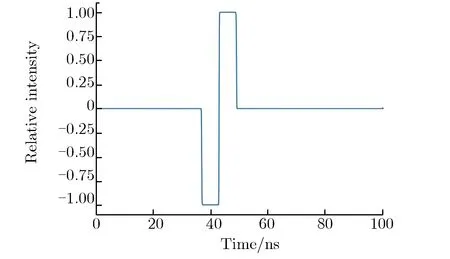
(b) Signal 2

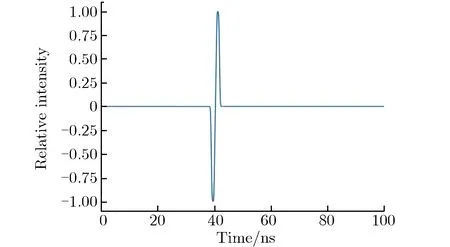
(c) Signal 3图3 3种激励源信号时域波形Fig.3 Time domain waveform of three types of excitation source signals

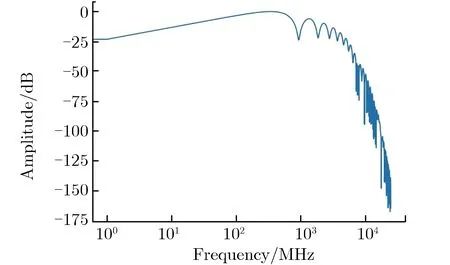
(a) Signal 1

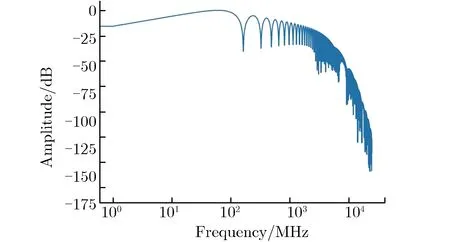
(b) Signal 2

(c) Signal 3图4 3种激励源信号归一化频谱图Fig.4 Normalized spectrums of three excitation source signals

根据GJB 8218-2014[21],采用脉冲的幅频特性曲线上包含97%脉冲能量的频段[0,f97]作为脉冲的主频段。其中,f97为脉冲的上限频率,可表示为

(6)

其中:A(f)为脉冲的幅频特性;f为频率。

根据此定义,图4中3种激励源信号的上限频率分别为3 284, 2 687, 1 314 MHz。

在CST Design工作室中连接电路,裸导线一端接激励源端口,另一端接50 Ω负载,模拟实际工作状态,电路模型如图5所示。图5中,P1与P2为端口处的探头;N1_SW_1与N2_SW_1分别为Schematic Block的输入端与输出端。

图5 电路模型Fig.5 Model of the circuit

2.1 仿真结果

2.1.1 激励源信号1

为方便描述,激励源信号辐照裸导线产生的耦合电压峰值均取绝对值。当激励源为信号1时,耦合电压峰值Vp随线缆长度l的变化关系如图6所示。由图6可见:l为1～6 cm时,Vp从约20 V线性增长至约160 V;当l为6～25 cm时,Vp由最大值约160 V下降至约120 V;当l大于30 cm时,Vp在120 V附近振荡。

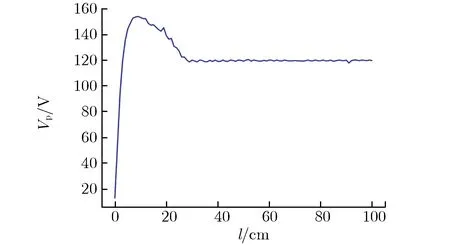
图6 耦合电压峰值随线缆长度的变化关系Fig.6 Vp vs. l

上升沿tr表示感应信号从10%电压峰值增至90%电压峰值的时间间隔。耦合电压上升沿tr随线缆长度l的变化关系如图7所示。

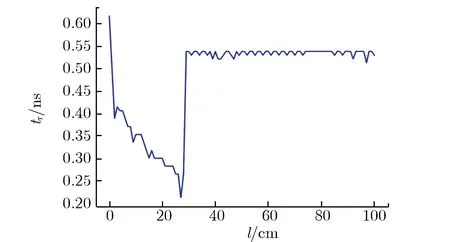
图7 耦合电压上升沿随线缆长度的变化关系Fig.7 tr vs. l

由图7可见:当l为0～30 cm时,tr随l增大而减小,由约0.6 ns减小至约0.2 ns;当l约为30 cm时,tr急剧上升至约0.55 ns;当l为30～100 cm时,tr基本维持在约0.55 ns;tr最小值与图3(a)中激励源信号1的脉冲宽度基本接近。

由上述结果可得,激励信号1的线缆耦合电压峰值Vp可表示为

(7)

其中:E为平面波辐照电场强度;ls为耦合电压开始收敛时所对应的线缆长度。

线缆长度为6 cm时,线缆耦合电压V随时间t的变化关系如图 8所示。

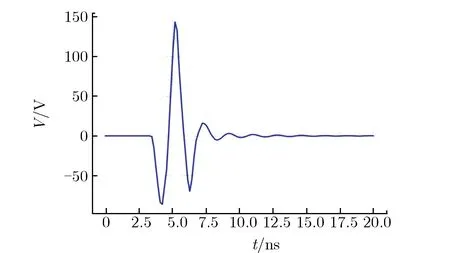
图8 线缆长度为6 cm时,线缆耦合电压随时间的变化关系Fig.8 V vs. t when the cable length is 6 cm

2.1.2 激励源信号2

当激励源为信号2时,耦合电压峰值Vp随线缆长度l的变化关系如图9所示。由图9可见:当l为1～180 cm时,Vp从约50 V增至约380 V;当l大于180 cm时,Vp稳定在约380 V。

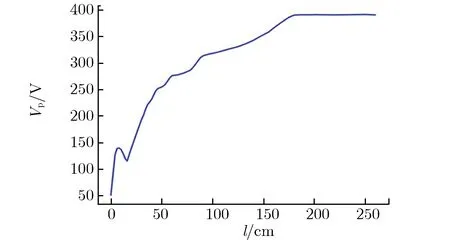
图9 耦合电压峰值随线缆长度的变化关系Fig.9 Vp vs. l

耦合电压上升沿tr随线缆长度l的变化关系如图10所示。

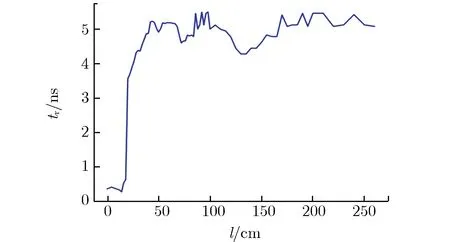
图10 耦合电压上升沿随线缆长度的变化关系Fig.10 tr vs. l

由图10可见:当l为0～40 cm时,随l的增加,tr整体呈增大的趋势;当l大于40 cm时,tr基本在4.5～5.5 ns之间波动。

与第2.1.1节中信号1相比,信号2的脉冲宽度约为信号1的6倍,Vp最大值约为信号1的3倍,tr最大值约为信号1的10倍。

线缆长度l为200 cm时,线缆耦合电压V随时间t的变化关系如图11所示。

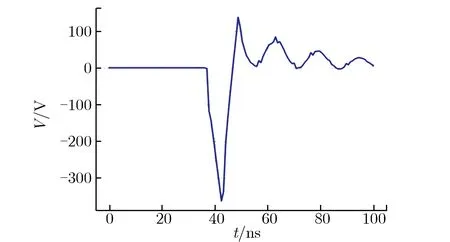
图11 线缆长度为200 cm时,线缆耦合电压随时间的变化关系Fig.11 V vs. t when the cable length is 200 cm

2.1.3 激励源信号3

当激励源为信号3时,耦合电压峰值Vp随线缆长度的变化关系如图12所示。

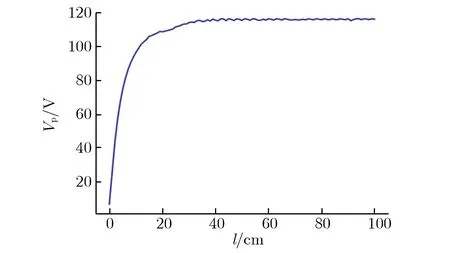
图12 耦合电压峰值随线缆长度的变化关系Fig.12 Vp vs. l

由图12可见:当l小于6 cm时,Vp随l的增加呈线性增大的趋势;当线缆长度为6～40 cm时,Vp随l的增加缓慢上升;当l大于40 cm时,Vp在115 V附近波动。

耦合电压上升沿随线缆长度l的变化关系如图13所示。

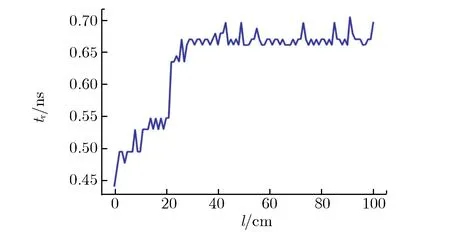
图13 耦合电压上升沿随线缆长度的变化关系Fig.13 tr vs. l

由图13可见:当l为1～32 cm时,随l的增加,tr整体呈增大的趋势;当l大于32 cm时,tr基本在0.66～0.70 ns之间波动。

与第2.1.1节中信号1相比,激励源信号3的上升沿略大,随l的增加,Vp上升较为平缓,最后的稳定值与激励源信号1差别不大。

线缆长度l为6 cm时,线缆耦合电压V随时间t的变化关系如图14所示。

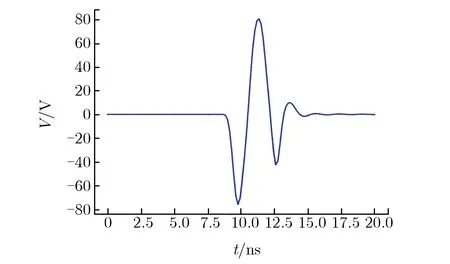
图14 线缆长度为6 cm时,线缆耦合电压随时间的变化关系Fig.14 V vs. t when the cable length is 6 cm

2.2 仿真结果对比

3种激励源信号的线缆耦合仿真结果如表2所列。表2中:λf为中心频率对应的波长;Vp,max为Vp的最大值;Vp,sta为Vp的稳定值;tr,sta为tr的稳定值;ls为Vp,sta对应的线缆长度。

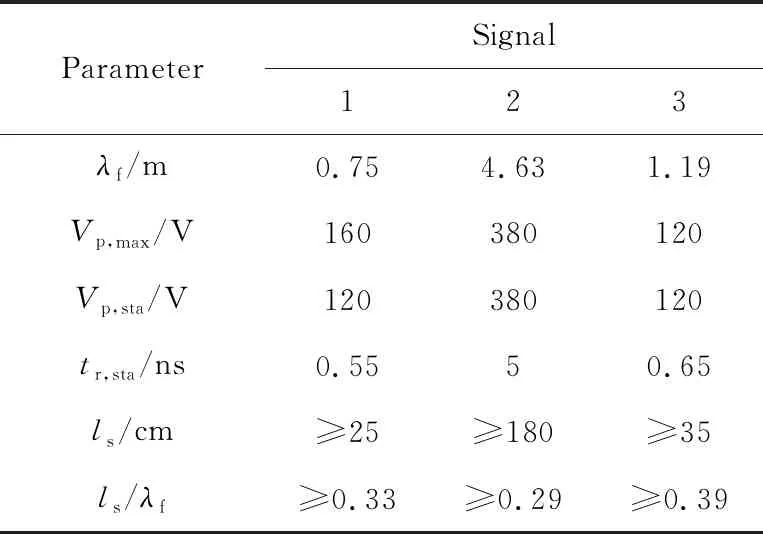
表2 3种激励源信号的线缆耦合仿真结果Tab.2 Simulation results of cable coupling for three types of excitation source signals

由表2可知:在超宽带高功率脉冲辐照下,较长线缆的耦合电压峰值Vp在百伏量级;Vp及tr均随着l的增加而增大,并逐渐收敛趋于稳定;ls/λf约为0.3,甚至更大。对于上升沿极短的超宽带高功率脉冲,当传输线缆较短时应当有更高的防护要求,传输线缆较长时防护要求略低;对于脉冲宽度较宽的超宽带高功率脉冲,传输线缆较长时耦合电压较大,对防护器件耐受提出更高的要求。

3 结论

基于时域有限差分法,利用CST模拟仿真了UWBHPP对裸露导线的耦合响应特性。仿真表明:线缆耦合电压峰值及上升沿受UWBHPP宽度的影响较大,当脉宽显著变大时,耦合电压峰值及上升沿会成倍数增大;线缆耦合电压峰值稳定值对应的线缆长度与中心频率对应波长的比值约为0.3;应对上升沿较快的UWBHPP,当线缆较短时,需额外考虑耦合电压峰值。仿真结果可为防护装备的防护设计提供一定的参考。