气流床煤气化熔渣流动行为参数预测模型的研究进展
2023-10-20赵超越白永辉宋旭东苏暐光王焦飞于广锁
赵超越,白永辉,宋旭东,苏暐光,吕 鹏,王焦飞,于广锁,2,姚 敏
(1.宁夏大学 化学化工学院 省部共建煤炭高效利用与绿色化工国家重点实验室,宁夏 银川 750021;2.华东理工大学 洁净煤技术研究所,上海 200237)
0 引 言
气流床(EFB)气化具有碳转化率高、煤种适应性强、燃料进料灵活以及技术性能优良等优点,是我国煤炭大规模利用的优先选择[1-2]。原料煤粉或水煤浆经高压喷入EFB气化炉内,在高温下(1 300~1 500 ℃),原料与气化剂(O2/H2O)接触,煤中有机物经热解、气化生成合成气,无机物经高温转化为熔渣沿气化炉内壁流动进入水浴,在水浴中凝固并通过锁斗排出[3]。EFB气化炉工艺温度和气化装置的长期稳定运行与灰渣流动行为关系密切[4]。煤灰的熔融特性是描述升温过程中煤灰变成熔渣的行为;黏温特性是高温液相熔渣逐渐冷却成固相过程中的行为变化,即通常采用灰熔融特性和黏温特性描述煤灰的流动行为[5]。煤灰熔融特性是选择气化炉用煤的重要指标,灰熔融温度(AFTs,包括变形温度(TD)、软化温度(TS)、半球温度(TH)和流动温度(TF))是评价煤灰熔融特性最直接的参数[6]。煤灰的黏温特性一般采用黏温曲线描述煤灰在高温下形成熔渣时黏度与温度间的关系。高温熔渣在冷却过程中的黏度变化、结晶等行为也是描述结渣过程中熔渣黏温特性的重要参数,并为气化炉用煤选择提供重要指导[7]。AFTs和黏度是最直观的参数,是评价煤灰流动行为最根本的标准。
为保证EFB气化炉顺利运行,结合工业实际要求,一般要求煤灰TF在1 380 ℃左右,在该运行温度下煤灰的黏度在2.5~25.0 Pa·s[8-9]。高AFTs煤(TF>1 500 ℃)在EFB气化过程中造成堵渣、结垢、熔融、团聚和沉积等问题;低AFTs煤冲刷炉体,不能形成合适的挂渣保护层;高(低)AFTs煤都易造成炉体损伤,从而缩短EFB气化炉的使用寿命[10-12]。黏度过高,引起结渣堵渣问题;黏度过低,耐火砖被侵蚀,加快脱落,冲刷气化炉内壁。
煤在EFB气化炉内的化学反应处于高温高压且湍流多相反应的苛刻条件下[13],该苛刻条件决定了煤在气化过程中的灰流动行为难以实时测量,同时试验人员的主观性和测试设备会造成较大的差异,获取熔渣流动行为参数困难大,极大促进了熔渣流动行为预测模型研究工作。通过预测煤灰的熔融特性和黏温特性参数不仅可以验证数据的可靠性、替代繁琐的试验,还可预测原料在气化炉中出现问题而进行相关调整,极力避免结渣堵渣现象造成炉渣堵塞和气化炉非计划停工[14]。颜婷珪等[15]基于宏观性质测试方法和模拟计算方法详细综述煤灰流动性研究方法,其中包括软件预测分析法,但并未提及相应的预测模型公式及适用范围;另外,有研究人员论述了煤灰的灰熔融温度预测方法,但未涉及其他熔渣参数[16]。因此,笔者分别介绍不同流动行为参数、各预测方法的优缺点、应用范围及相关模型,并分析预测公式与真实试验结果的误差对比,以期对指导EFB气化过程中熔渣流动行为的准确预测提供借鉴。
1 熔渣流动行为参数
熔渣的流动行为包括灰熔融特性和黏温特性,是选择气化用煤的重要依据,也是影响气化炉长期顺利液态排渣及稳定操作的关键因素,因此,为达到更精准预测效果,需寻找影响煤灰熔融特性和黏温特性的参数。
1.1 熔融特性参数
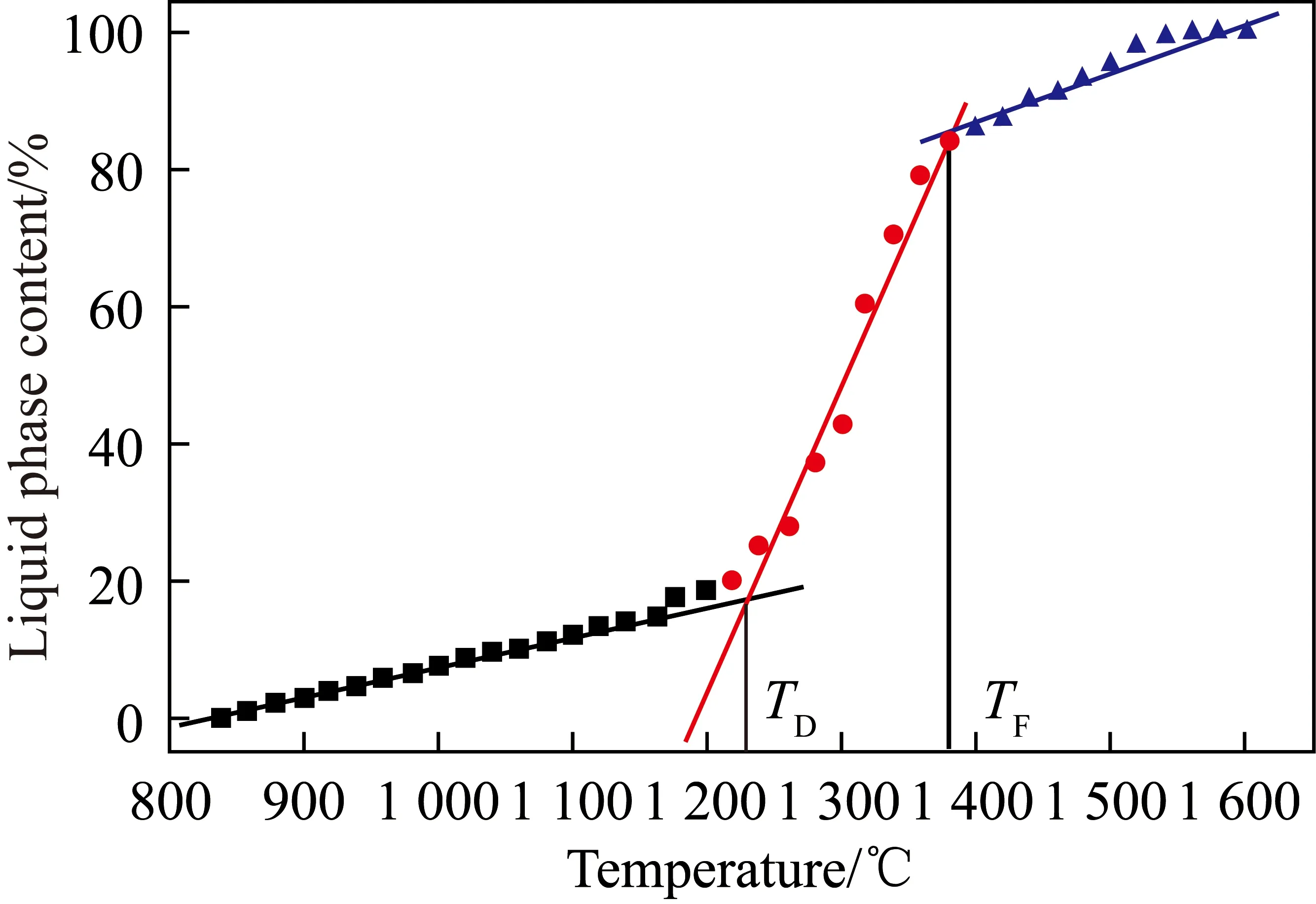
煤灰熔融特性是指用于描述煤灰在高温下固相转变为液相的过程。煤中成分复杂,没有严格物理意义的熔点,故定义了TD、TS、TH、TF四个特征温度,即AFTs来描述其熔融过程。煤灰温度达到TD时,煤灰开始熔融并产生一定黏度;当温度达到TS时,煤灰黏度进一步增大[4]。当温度达到TF时,黏附现象已经十分严重,此时存在大量液相。基于上述煤灰熔融的主要过程,TF通常被认为是评价煤灰的流动行为最根本的标准,预测TF具有一定可靠性[17-18]。高温下熔融特性由矿物质的熔融性和热稳定性决定,表征煤灰熔融性的参数除AFTs外,还有初始液相温度Tini、液相含量对应的温度(全液相温度Tliq,含90%液相对应的温度T90、100%对应的液相温度T100)、最后一个固相对应的温度Tend等参数。AFTs作为直接判断煤灰熔融特性的参数,其传统测试方法是将煤灰制作成标准灰锥,用灰熔点测定仪观察升温过程中灰锥的熔融程度,根据GB/T 219—2008《煤灰熔融性的测定方法》判断出4个特征温度是最常用的煤灰熔融性测试方法;也可采用热机械分析仪测定AFTs,用体积变化速率、峰形宽度和高度获得液相含量、收缩率等灰熔融相关的参数[7]。
煤灰的化学组分主要包括SiO2、Al2O3、Fe2O3、TiO2、CaO、MgO、Na2O、K2O、SO3、P2O5等10种氧化物(煤灰中还存在SO3,但在加热过程中SO3会作为气体逸出,预测时一般不考虑)。上述氧化物根据其性质可分为酸性氧化物(A:SiO2、Al2O3、P2O5、TiO2)和碱性氧化物(B:Fe2O3、CaO、MgO、Na2O、K2O)[19]。酸性氧化物易增强聚合物的稳定性从而提高煤AFTs和黏度;反之,碱性氧化物会抑制煤中聚合物形成,或疏松硅酸盐网络结构[20]。煤灰成分复杂,对于高硅铝煤、高钙高铁煤等同一类型的煤,也可采用添加煤灰中的单一组分来调控煤灰AFTs,但无法精准预测煤灰的流动行为。为更好地描述煤灰组分对煤灰流动行为的影响,根据不同类型煤灰组成提出2个参数:硅铝比(S/A,SiO2/Al2O3)和碱酸比(B/A=w(Fe2O3)+w(CaO)+w(MgO)+w(Na2O)+w(K2O)/w(SiO2)+w(Al2O3)+w(P2O5)+w(TiO2),或酸碱比(A/B)),可以很好预测煤灰流动行为的变化趋势[14]。另外,从矿物质角度分析,煤灰在高温熔融过程中逐渐生成的耐熔矿物质、助熔矿物质等矿物质影响AFTs。不同气氛(氧化性气氛、弱还原性气氛、强还原性气氛等)条件下会改变煤灰组分(Fe)的价态,富铁煤在不同气氛下的AFTs大小的规律为:强还原气氛>氧化性气氛>弱还原性气氛[21]。
1.2 黏温特性参数
煤灰的黏温特性一般用来描述煤灰在高温下形成的熔渣黏度与温度之间的关系。根据体系中相平衡、黏性流体的活化能和煤灰的化学组成等影响因素,一般常采用黏度、临界黏度温度(TCV)、Tliq等参数评价熔渣的黏温特性[22]。熔渣黏温曲线的测量方法:将制备好的煤灰根据其AFTs或Tliq放进高温炉中预熔,将冷却后的熔渣放入测试坩埚,在高温旋转黏度仪中以3 ℃/min的降温速率获得不同温度下的黏度[23]。当熔渣温度高于Tliq时,熔渣结构是影响黏度的主要因素;当熔渣温度低于Tliq时,析出的固相是影响黏度的主要因素[24]。根据熔渣在低于Tliq时的黏度特性,熔渣类型一般分为玻璃渣和结晶渣。对于玻璃渣,黏度随温度的降低逐渐增大;结晶渣的温度在TCV以下,其黏度迅速升高,由于晶相的存在,黏度的增加会导致熔渣堵塞和气化炉非计划停工[25-26]。晶体的形成取决于复杂多组分体系内的相平衡、固体析出速率或析出晶体的几何尺寸,其晶体成核和生长动力学对形成晶体的大小、数量和形状也有一定的影响[27]。
煤灰流动行为参数的影响因素可概括为内部因素(煤灰组分)和外部因素(气氛、压力)[28]。改变操作条件是通过改变单个元素的价态或矿物成分的存在形式改变AFTs和黏度,而煤灰化学成分是通过寻找煤灰化学组成及比值与煤灰流动行为参数之间的定性或定量关系来建立预测模型[19]。AFTs和熔渣黏度参数测量不仅复杂且耗时,重复性和准确性较差。因此,需借助煤灰组分及AFTs、Tliq、TCV、S/A、B/A(或A/B)等煤灰流动行为参数来建立预测模型,同时弥补高温表征手段的不足,对气化炉选择煤样具有一定指导意义。
2 预测模型方法
根据构建预测流动性参数的处理方法,可分为回归分析法、软件预测法(FactSage热力学模拟软件、LAMMPS动力学模拟软件)、数学建模法(人工神经技术(反向传播算法(BP)、支持向量机(SVM))和离子势(平均摩尔离子势(Ia)、金属离子电势浓度(CMP))预测法。每种预测方法具有一定的优缺点,熔渣参数不同,可选择不同预测方法,也可选用多个方法联合进行预测。
2.1 回归分析法
回归分析法可通过数据中的因变量与某个或某些自变量的相关关系建立一个相关性较好的回归方程(即函数表达式),是前期预测煤灰AFTs和黏度变化常用的分析方法。通过拟合大量经典煤灰的真实数据,借助Matlab、最小二乘法、偏最小二乘法等优化方法对多个煤灰化学组成或比值参数进行多元线性回归拟合。引入相关参数R描述拟合的相关程度,若R>0.7,相关度一般,在接受范围内;R>0.8,相关度较高;R>0.9,相关度非常高,故可通过R判断该预测模型的预测效果。
2.2 软件预测法
随热力学、动力学模拟软件的普及,为预测煤灰的流动性参数提供了便捷。FactSage热力学模拟软件遵循Gibbs能最小化原则,确定固相形成在能量上是否有利[29];LAMMPS分子模拟动力学软件模拟分析晶体成核和生长动力学对煤灰形成的晶体大小、数量和形状存在一定影响[22]。采用软件预测法具有省时省力,精度高等优点,借助软件建立有化学意义的关联参数预测煤灰熔渣的参数。
2.2.1 FactSage热力学模拟软件
FactSage热力学软件作为化学热力学领域中完全集成数据库的最大计算系统之一,常用来计算煤灰中多元相平衡及矿物熔融过程的变化,以及预测高温下灰渣的状态、性质[30]。FactSage热力学软件中的“Equilib”模块计算出不同温度下煤灰熔融过程的物相变化规律,计算发现FactSage模拟结果与试验结果基本一致[31-32];“Viscosity”模块模拟计算黏度变化,以便较准确找到最佳配比调整配煤方案,对试验具有一定的指导和参考意义[33]。王芳杰等[20]通过试验测定的黏度值与Factsage软件预测黏度值基本一致;“Phase Diagram”模块探究相平衡,固、液相及等温线变化;“Reaction”模块热化学角度分析煤灰在高温下的反应,以及相应的吉布斯自由能(ΔG)、焓变(ΔH)、熵变(ΔS)等。FactSage软件还可用于模拟计算特定温度下的晶相组成、液-固含量以及黏度等,从热力学角度分析并构建具有化学意义的参数模型。
2.2.2 LAMMPS动力学模拟软件
LAMMPS分子动力学(MD)方法依据Newton力学来模拟分子体系的运动,获得分子运动轨迹,进而计算体系中的宏观热力学性质和动力学性质(如动能、势能、压力、扩散系数、传播系数、结构因素、谱密度函数、分布函数等)[34];通过选择合适的势函数模拟计算熔渣微观结构、原子轨迹等,得到熔渣的微观结构信息,根据径向分布函数,获取配位数、键长、键角等数据信息,以及四面体结构、氧键单元,从而进一步构建氧键与黏度、TCV的关联式。目前该模拟软件已广泛应用于玻璃、冶金渣和煤灰渣等熔体微观结构的研究[35-36]。
2.3 数学建模法(优化)
智能算法可对原始数据进行加工和分析,探寻未知的内在规律。数据挖掘的方法主要分为传统的统计学方法、粗糙集理论方法、决策树理论方法和人工神经网络理论方法。其中,人工神经网络不仅可承受异常数据的干扰,具有优异的非线性泛化能力及并行处理复杂信息的能力,且具有自组织、自适应、分布式记忆(存储)等优势,被广泛使用。常见的人工神经网络模型、运行模式及主要应用[37]见表1。
目前,除上述BP神经网络优化算法用于煤样数据优化外,SVM算法也具有良好的自学习能力,适合小样本训练,较好解决神经网络的欠学习和小样本中局部极小点等问题,且基于其结构风险最小化原则,其在统计学方法中也独树一帜[44-45]。下面将分别介绍BP神经网络优化和SVM这2种算法。
2.3.1 BP神经网络模型
BP神经网络以其预测精度高、结构简单、自学习、自组织、自适应能力强等优点得到了广泛应用。主要通过误差的反向传播自动调整网络结构的参数,对于给定的输入,产生最期望的输出。在内部机制和联系不确定的情况下,BP神经网络被认为是一种高精度的模型方法。LIANG等[46]采用BP神经网络模型(图1)来探索煤灰的化学组成与其TD之间的关系,采用均方误差(MSE)(评价一组数据的离散程度)评估BP网络训练结果的稳定性,当MSE达到最小值时,BP神经网络预测取得较好的精度,其最大相对平均误差为6.67%。

图1 BP网络模型建立流程Fig.1 Flow chart of the network model establishment
BP神经网络进行数据优化时存在学习率参数的选取、收敛速度慢、易陷入局部极小值点及网络自身结构的选取等问题。近年来,研究学者们采用自身算法的直接改进、与其他智能算法联用及集多算法优势于一体的高性能神经网络模型对BP进行优化[47-48](表2)。

表2 优化BP神经网络的算法Table 2 Algorithms for optimizing the BP neural networks
2.3.2 SVM算法模型
SVM一般用来解决分类和回归问题,研究人员常用SVM算法来优化熔渣参数预测AFTs。WANG等[52]基于遗传算法建立了GA-SVM预测AFTs模型,预测较准确,发现该模型适用于学习小样本问题。XU等[53]模拟退火算法优化SVM得到预测TD的模型,并对电厂实测数据进行预测检验,发现模型预测精度较高。王红娜[54]建立了中国典型78种煤灰数据对SUM算法预测的初始训练样本和检验样本,预测20种单煤、13种混煤(2种煤掺混)和23种混煤(3种煤掺混),该试验发现23种混煤的效果最好,其MAPE(平均绝对百分误差)=1.24%,MSE=868;其次为20种单煤的效果较佳,MAPE=6.23%,MSE=8 159;2种掺混效果较差,MAPE=6.77%,MSE=16 158。出现较大预测误差的原因在于上述优化SVM算法对同一类型的煤种预测更为准确。
2.4 离子势预测模型
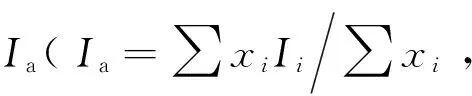
3 熔渣流动行为参数的预测模型
根据熔渣流动行为的评价参数,下面将分别按照预测熔渣熔融特性和黏温特性两部分进行介绍。
3.1 预测熔渣熔融特性参数的模型
从煤灰结构固液两相变化的本质可以看出,熔渣的AFTs和Tliq参数是典型用于预测熔渣熔融特性,通常采用煤灰组分及参数(S/A、B/A(或A/B)、Ia等)、Tliq等参数建立预测熔渣黏温特性参数。
3.1.1 预测AFTs的模型
1975年,WINEGARTNER和RHODES采用回归分析方法探索49个灰化学成分参数与AFTs间的定量关系,其分析误差为27 ℃。SEGGIAN也基于上述49个参数预测了260种不同组分的煤和35种生物质的AFTs和TCV,标准差约50 ℃,再次证明灰化学成分参数对煤灰流动性参数预测效果较好[57-58]。LIANG等[46]以煤灰中的酸性氧化物、碱性氧化物及B/A为自变量,用回归分析方法探究TD与上述3种自变量间的线性关系,拟合预测有15%误差,计算结果偏差约在100 ℃以内,故线性回归可以预测煤灰TD的变化趋势。
1)构建FT-煤灰组分参数的模型。XU等[59]采用最小二乘法拟合181个典型煤灰(A/B在0.55~6.96),TF与灰化学组成(R=0.934)的关系为
TF=0.091w(SiO2)2+ 0.270 1w(Al2O3)+0.148 9w(CaO)2+
0.208 8w(Fe2O3)2+ 6.827w(SO3)2+ 4.564w(TiO2)2+
0.523w(MgO)2+2.852w(Na2O)2+0.967w(K2O)2+
9.891(A/B)+837.5 。
(1)
刘硕等[60]借助Matlab软件和最小二乘法等多元回归拟合方法分别进行拟合,其预测公式分别为
Matlab软件拟合:TF=1 194.81-3.63w(SiO2)+2.76w(Fe2O3)+1.92w(Al2O3)+2.35w(CaO)+0.95×w(MgO)+10.66w(K2O)-21.74w(SiO2)-0.47×w(SO3)+66.31(A/B),R=0.78。
(2)
最小二乘法:TF=1 392.44-4.63w(SiO2)-1.92×w(Fe2O3)+3.24w(Al2O3)+0.3w(CaO)-11.68×w(MgO)-17.60w(SiO2)+5.50w(SO3)+4.47(A/B),R=0.83。
(3)
结果表明利用最小二乘法优化的回归分析法建立的预测模型的预测效果最佳。