生本理念下高中数学例题教学
2023-10-20游华秀
游华秀
(上杭县第一中学,福建 上杭 364200)
教师的课堂教学要能为学生搭建一个适宜学习的方式和平台.基于学情、站在学生学习立场的精心设计,对学生学习目标的达成、学习方式的优化、学习方法的掌握、学习能力的提升和思维品质的优化大有裨益.然而,在解题教学中,笔者发现不少教师将教学设计的重心放在展示自己的解题能力上,不断地抛出不同解法,强化解题技巧和套路的训练,忽视思路的分析和解法的形成过程,忽略学生内在的数学思维活动.数学解题教学的关键应落实到何处?怎样落实才能更好地促进学生的学习?笔者谈谈自己的一些思考.
1 着眼点:点拨疑难,帮助学生摆脱学习困境
学生解题障碍主要体现在已有知识和经验无法与所求问题成功对接,解题过程出现思维短路.解题教学设计要切实以生为本,关注学生的所思所想,弄清学生“困”在何处?为什么会“困”?怎样想方设法突出重围?真正帮助学生释疑解惑,引导学生在探究破解问题的方法上下足功夫,让其摆脱学习困境才是解题教学设计的着眼点.

1)将C和l化为直角坐标方程;
2)求C上的点到l距离的最小值.
条件给出的椭圆参数方程和教材中以离心角为变量的形式不同,这是学生解题的受困之处.教师在解题教学设计时,可依托问题链驱动学生逐步破解:
问题1消元主要有哪些手段?怎样操作?



上述问题链循序渐进,慢慢地让学生找到平方相加消元法,即
(1+t2)2=(1-t2)2+(2t)2;

2 着力点:深挖本质,帮助学生实现学习迁移
能否抓住问题的本质决定了能否正确解决问题或解题方法是否简洁.解题教学的设计应着力帮助学生揭示概念、原理的相同或相通之处,深入探寻问题本源,指导学生总结解题方法的普遍性与特殊性,让学生懂得各种方法的来龙去脉,清楚不同方法之间的区别与联系,发展学生触类旁通的迁移能力.
例2已知函数f(x)=aex-1-lnx+lna.
1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
2)若f(x)≥1,求a的取值范围.
(2020年全国数学新高考Ⅰ卷第21题)


lna+x0-1=-lnx0.
易知x0与a的大小有关,当x∈(0,x0)时,f′(x)<0,函数f(x)单调递减;当x∈(x0,+∞)时,f′(x)>0,函数f(x)单调递增,从而
f(x)≥f(x0)=aex0-1-lnx0+lna
即
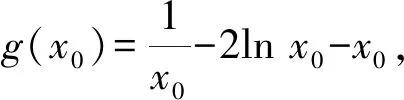
lna=1-x0-lnx0≥1-1-ln 1=0,
故a≥1.
解法2易证不等式ex>x-1,x-1≥lnx成立,可得
aex-1≥ax, -lnx≥-x+1.
当x=1时,上面两式取到等号,从而
aex-1-lnx+lna≥ax-x+lna+1,
只需要证
ax-x≥-lna,
即证
x(a-1)≥-lna.
当a≥1时,x(a-1)≥0≥-lna恒成立;当0 解法3由f(x)≥1,可得 aex-1-lnx+lna≥1, 即 ex-1+ln a-lnx+lna≥1, 亦即 ex-1+ln a+lna+x-1≥lnx+x=eln x+lnx. 令g(t)=et+t,则 g′(t)=et+1>0, 从而g(t)在R上单调递增,得 g(lna+x-1)≥g(lnx), 从而 lna+x-1≥lnx, 即lna≥lnx-x+1恒成立.令h(x)=lnx-x+1,得 当0 h(x)≤h(1)=0, 即 lna≤0, 故a≥1. 解法4aex-1-lnx+lna≥1,即aex-1≥lnx-lna+1.又函数g(x)=lnx-lna+1与h(x)=aex-1互为反函数,图象关于y=x对称,两个图象均与y=x相切,且相切时a取最小值.设切点横坐标为x0,则 g(x0)=lnx0-lna+1=x0, 且 求得a=1,故a≥1. 经过探究,教师要让学生明白:解法1根据f(x)的最小值去寻找x0的范围,再从中求得a的取值范围,分类讨论及隐零点的运用是常见思路;解法2通过放缩,将超越不等式转化为易解的不等式,这也是基本方法,不等式ex≥x-1和x-1≥lnx是学生必须熟记的重要结论,比解法1少了繁杂的讨论;解法3抓住了函数的结构特征,需要理解求解的思路,才能领会如此巧妙的做法;解法4在解法3的基础上,更进一步体现了数形结合的重要性,其实质是两个凹凸性不同的函数相切.让学生在探究中获得知识与方法的本源,不断修正错误思路,拓展创新优秀解法,实现由一题到一类的迁移. 教学是一项双向活动,学生是学习的主体,教师的解题教学不能只给出问题的答案,而应让学生深度参与解题方案形成的全过程,包括隐含条件的挖掘、关键信息的转换、重要的计算步骤等,不断强化才能将课堂所学内化为自己的基本经验,提升学生分析问题和解决问题的能力. 例3直线l过点P(-4,0),与⊙C:(x-1)2+y2=5交于点A,B,A是线段PB的中点,求直线l的方程. 以下是某教师高三复习课的教学片段: 方法1设直线l的方程为y=k(x+4),点A(x1,y1),B(x2,y2),将直线l与圆方程联立,可得 又A是线段PB的中点,则 2x1=x2-4, 得 故所求方程为 x±3y+4=0. 方法2设直线l的方程为x=my-4,与圆联立(下同方法1,略). 这是一题多解教学的常见误区,该教师只是抛出各种解法,没有帮助学生揭示不同解题方法的“源”与“流”.“方程思想”是解决解析几何题的基本思想方法,方法1“怎样解出k的值”是学生的一个难点,缺乏计算的过程,一步跨过学生未必能真正获解;方法3的实质是“方程思想”下的简解,精准点评才能让学生积累经验,才能避免让学生形成“总是用根与系数的关系”的错觉. 解题教学是启迪学生心智的重要途径.其教学设计不能只关注问题的模式识别、解题技巧的归纳、求解套路的训练,应该通过典型问题的分析,将思维的启迪落到实处,让学生学会深入分析题目所给的各个信息之间的关联,特别是在所求问题的目标引领下如何合理选择问题的求解策略,掌握理性思考问题的方法. ( ) (2022年全国数学新高考Ⅰ卷第8题) 分析此题的目标是求棱锥体积V,已知侧棱长l,自然会想到建立V与l的函数关系.如图1,设正四棱锥的底面边长为a,高为h,由题意可知球的半径R=3,又 图1 从而 l2=6h. 由l的取值范围可得 找出h,l,a之间的关系是求解此题的关键. 解法1(统一化为l)正四棱锥的体积为 设x=l2∈[9,27],则 利用导数求其单调性可得 故选C. 解法2(统一化为h)正四棱锥体积为 利用导数求其单调性可得 故选C. 解法3(统一成角)设正四棱锥高与侧棱的夹角为θ,AE=m,则在△AEP中, y=sinθcos2θ=-x3+x, 以上解法自然顺畅,学生的自然想法与数学思维方式的融合是启迪学生智慧的有效路径.解题教学需基于学科的整体高度,设计的关键要落在知识的交汇处,关注知识的整体关联,才能通过解题教学让学生实现知识内容结构化、求解方法系统化、迁移能力自动化.上述设计让学生充分经历了必备知识与关键能力的研习与运用,体现了目标引领下逻辑地思考数学问题的过程,展现了在情境活动思路探寻中“理性思维”的统领价值,对提升学生的思维能力大有裨益. 对解题过程的反思与总结是学生能力提升不可或缺的环节,这也是一种优秀的学习习惯.解题教学不可解完即止,应将“反思”与“解题”相互融合,包括知识的归纳、方法的提炼、错误的探源、思路的优化及对题目的再审视、再探索,不断提升学生的数学思维品质. 1)求a的值; 于是 联结PP1,BB1,AA1,不难发现PP1∥BB1∥AA1. 解题教学与解后总结反思密不可分,并非相互独立,更不是相互对立,而是互补地存在于教学过程之中.合理必要的反思有助于日后更好地进行教学设计,对师生都能起到极大的帮助. 数学解题教学设计既要深入研究数学课堂教学本身的规律,理解学生的学习心理、学习习惯和认知特点,还要领悟数学的基本思想和方法、解决问题的常用策略、课堂操作的基本路径,准确把握教学设计的关键点,抓实学生外显的学习过程,抓牢学生内在思维品质的优化,才能将数学能力的发展真正落到实处.3 着重点:经历过程,帮助学生获得学习经验

4 落脚点:启迪智慧,帮助学生学会理性思考




5 关键点:反思总结,帮助学生优化学习习惯