也谈自制简易密度计的竖直漂浮问题

邬启超

(苏州工业园区星湾学校,江苏 苏州 215021)

1 密度计的稳定平衡状态

漂浮在水中的物体有两个心,重心与浮心,重心是重力的作用点,浮心是浮力的作用点,浮心的位置就是那部分被排开液体重心的位置,[2]对于密度均匀的浮体,当其处在竖直漂浮状态时会有部分露出水面,故重心一定高于浮心,如图1所示.密度计属于非均匀浮体,且质量集中在底部,密度计竖直漂浮时便存在浮心高于重心的情况,[3]当竖直漂浮的密度计受到扰动时,重力与浮力的力偶矩是恢复力矩,如图2所示,因此平衡态稳定.生活中常见的密度计,上段细且粗细均匀,中下段稍大呈泡状,底部装有小铅粒或水银(密度大),这样可以在满足精确度的前提下尽量地提高浮心并降低重心,从而让密度计能够稳定竖直漂浮.

图1

图2

2 密度计浮心与重心间距与配重的关系

在实际制作简易密度计时会发现当密度计竖直漂浮后继续增加配重密度计会更稳定,这是为何呢?我们可以建构如图3所示的模型进行说明,假设密度计未加配重时的质量为m0,重心(C1)距密度计底部为h1,加入配重(以细沙为例)的重心(C2)距密度计底部为h2,此时密度计的总质量为M,密度计的重心距密度计底部距离可表示为

图3

(1)

由配重的质量与密度以及密度计的底部半径可以将h2近似表示成

(2)

将式(2)代入式(1),化简后得

(3)

若密度计在水中竖直漂浮,根据浮力等于重力易得浮心与密度计底部的距离为

(4)

由于密度计在液体中漂浮时(浮力等于重力),必有浮心与重心在同一铅直线上,否则无法满足力矩的平衡.式(4)-式(3)得两心距离为

(5)

因为浮心高于重心时密度计可以竖直漂浮,可以把浮心等于重心看作是此状态的极限情况,令式(5)等于0,解得此时密度计的质量为

(6)

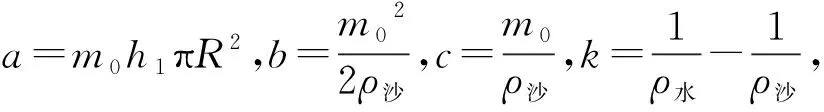
(7)

由式(7)可知,当M≥M1时L随M增大是单调递增的,因此在密度计质量达到M1后随着配重的增加,当密度计受到扰动后恢复力矩将更大,使得竖直漂浮状态更稳定.

3 浮心低于重心时竖直漂浮状态的讨论

(8)

将式(3)与式(4)代入式(8),使式(8)成立,密度计质量M须满足

(9)

M2k+2cM-2(a+b)≥0,

(10)

表1

事实上,对于一个漂浮体,其稳定平衡的充分必要条件是重心与浮心的高度差在浮力等于重力这一限定下取极小值.[3]在实际制作简易密度计时,随着配重的增加密度计静止时的状态逐渐趋于竖直方向,可见,随着配重质量的变化密度计会通过调整倾斜角度来实现极小值的满足,而极小值趋近于0.